附加频率控制下并网换流器的动态惯量及其量化评估

陈 湘，付 强，宾子君，肖先勇，孔祥平

（1.四川大学电气工程学院，四川省成都市 610044；2.国网江苏省电力有限公司电力科学研究院，江苏省南京市 211103）

0 引言

为实现“碳达峰·碳中和”目标，中国正加速构建以新能源为主体的新型电力系统。新能源通过电压源型换流器（voltage source converter，VSC）接入电网，而传统矢量控制下VSC 输出的有功功率基本与电网频率解耦，无法像同步发电机一样提供惯量和一次调频等频率支撑，恶化了功率扰动下电力系统的频率动态特性［1-4］。针对这一问题，学者们提出了多种虚拟惯量控制策略，按实现方式可分为构网型虚拟同步发电机控制［5-8］和跟网型附加频率控制［9-12］两类。其中，跟网型附加频率控制通过引入额外的频率控制环节来实现虚拟惯量控制，无须对现有成熟的跟网型控制系统进行重大修改，是本文重点研究的控制技术。在新能源大规模并网的背景下，并网换流器对系统频率动态特性的影响逐渐凸显，掌握并网换流器的惯量特性以及惯量量化评估是优化系统惯量响应、保障频率稳定的重要基础。

为量化并网换流器的惯量支撑能力，传统的惯量评估方法基于同步发电机分析框架下的惯量模型，给出了并网换流器的等效惯量常数［13-14］。这种方法忽略了并网换流器的控制特性，认为其提供的惯量等同于频率控制环节中的惯量设计参数。实际上，并网换流器惯量还受其他控制环节影响，呈现出受约束、时变、非线性等复杂特性［15-16］。在不同控制策略下，即使频率控制环节中的参数设置一致，在同样的低频事件中，并网换流器仍表现出不同的有功响应特性［17］。因此，传统惯量评估方法无法反映控制器动态特性对并网换流器惯量产生的影响，在精确评估换流器惯量时存在一定误差。

为克服传统方法的不足，大量文献对并网换流器惯量响应的动态过程展开了研究，指出大量控制参与下，并网换流器惯量不是常数，而是时变的传递函数。文献［18］给出了双馈风机惯量的传递函数表达式，将其常数项作为风机的等效惯量。文献［19］在文献［18］的基础上，提出了一种新的惯量构造方式，并引入动态惯量的概念来分析风机的惯量响应。本文采用动态惯量来描述传递函数的形式，突出了其与惯量常数的区别。文献［20］以同步发电机转子运动方程为基础模型，推导了附加频率控制下双馈风机的动态惯量。文献［21］基于双馈风机的并网频率响应模型推导其惯量，并利用劳斯近似给出了常数表达式。与惯量常数相比，动态惯量强调了控制器动态特性的影响，较为准确地描述了并网换流器惯量的时变特性，但却无法量化并网换流器的惯量支撑能力。目前，针对动态惯量量化评估的研究较少，文献［18，21］通过忽略动态惯量中的高阶项，并将其简化为常数，从而实现量化评估，但这种方法不能反映系统特性对动态惯量的影响，难以实现准确的量化。

综上，为提升并网换流器动态惯量量化评估结果的准确性，本文提出了一种基于并网系统主导特征模态的换流器动态惯量量化评估方法。首先，针对定直流电压控制和定有功功率控制这两类主流的控制方式，分别推导了附加频率控制下并网换流器的动态惯量，明确了其时变特性；然后，基于所提量化评估方法解析了并网换流器在主导特征模态下的惯量常数表达式，分析了多种因素对惯量的影响机制和规律；最后，基于时域仿真模型验证了所提方法和分析结论的准确性。

1 并网换流器及其附加频率控制

1.1 并网换流器的拓扑与控制结构

图1 为并网换流器在矢量控制基础上引入频率控制后的拓扑与控制结构。图中：下标“ref”表示对应变量的参考值；下标“d”、“q”分别表示d轴、q轴分量；Pin为并网换流器直流侧的输入功率；C、Vdc分别为直流侧的电容、电压；Vc、θc分别为并网换流器的输出电压幅值、相角，其dq轴分量为Vcd+jVcq；Pc、Qc分别为并网换流器的有功、无功输出功率；Pc+jQc为并网换流器的输出功率；Iabc为并网换流器输出电流的三相值，其dq轴分量为Id+jIq；Vpcc∠θpcc为并网的节点电压，其dq轴分量为Vd+jVq；Vpcc、θpcc分别为并网的节点电压幅值、相位；Xf、Xg分别为滤波电抗、线路电抗；ωpll、θpll分别为锁相环（phase-locked loop，PLL）输出的频率、相位。

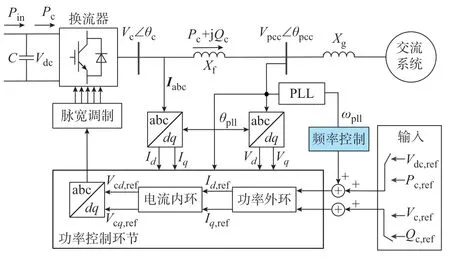
图1 并网换流器的拓扑与控制结构Fig.1 Topology and control structure of grid-connected converter

本文重点关注两类并网换流器：一类是采用定直流电压控制的并网换流器（VSC with DC voltage control，VSC-DC）；另一类是采用定有功功率控制的 并 网 换 流 器（VSC with active power control，VSC-AP）。这两类控制除控制目标不同外基本一致，其中PLL 可快速锁定电网的频率和相位，并基于此实现d、q轴控制变量解耦。因此，传统矢量控制下并网换流器输出的有功功率与电网频率解耦不具备调频能力。为解决这一问题，普遍的策略是引入频率控制环节，由PLL 提供节点电压的频率信号，并通过频率控制环节改变有功控制外环的参考信号，实现并网换流器参与频率调节。

1.2 附加频率控制下传统惯量常数的定义

对比VSC-DC 和VSC-AP，其附加频率控制下惯量常数的定义略有不同。

对于VSC-DC，电容与同步发电机转子具有相似的动态特性，按照同步发电机惯量常数的定义可以得到电容的虚拟惯量常数［9，22］。VSC-DC 直流侧电容在标幺值下的动态方程如式（1）所示。

式中：Hv为直流侧电容的虚拟惯量常数；t为时间；Vdc，N为 直 流 侧 电 容 电 压 的 额 定 值；Sc，N为VSC-DC的额定功率。

与同步发电机不同，Hv衡量的是功率-电压范畴下的惯量。为使直流侧电容的电场能量能够参与频率响应，通过比例控制将电网频率与直流电压参考信号耦合起来，使VSC-DC 产生功率-频率范畴下的惯量。

式中：ΔVdc，ref为直流电压参考信号的变化量；ω0为电网频率的稳态值；Kdc为VSC-DC 频率控制中的比例系 数；Hc，dc为VSC-DC 的 惯 量 常 数，即 理 论 设 计 的惯量。

对于VSC-AP，通过频率控制环节得到电网频率的差分和微分信号，并将其与有功功率参考信号耦合起来以产生惯量，如式（3）所示，其有功响应的能量通常来自VSC-AP 直流侧的储能或风机转子［10-11］。

式中：ΔPc，ref为有功功率参考信号的变化量；Kp、Kd为VSC-AP 频 率 控 制 中 的 比 例 系 数；Hc，p、Dc，p分 别为VSC-AP 的惯量、阻尼常数，即理论设计的惯量、阻尼。

值得注意的是，式（2）和式（3）中并网换流器的设计惯量是在忽略原有控制器动态的理想情况下得到的，即认为频率控制环节产生的控制信号变化能够被其他控制环节瞬间响应并跟踪。实际上，并网换流器包含了功率、电压、电流和相位等多个控制环节，其动态响应的时间尺度分布于毫秒至秒级之间［23］，如附录A 图A1 所示。并网换流器外环控制的响应时间远久于内环电流控制、脉宽调制等控制环节。因此，本文主要研究电压控制和功率控制时间尺度下，控制器动态对并网换流器惯量的影响。

2 并网换流器的传递函数模型

考虑到惯量响应对应的时间尺度，本文在建模中忽略高频动态环节、换流器拓扑级动态过程及其功率损耗、滤波电容和线路电阻的影响、电流内环的动态。在推导过程中，时间和惯量的单位是s，控制器积分系数的单位是rad/s，其余量均采用标幺值，下同。

2.1 VSC-DC 的传递函数模型

VSC-DC 输出功率在PLL 坐标系下可表示为：

设Vpcc∠θpcc的电压方向在稳态时与其d轴方向重合，即Vd0=Vpcc0且Vq0=0，下标“0”表示对应变量的稳态值。由此可得VSC-DC 输出功率的线性化方程如式（5）所示。

式中：Δ 表示对应变量的变化量。

忽略VSC-DC 的开关损耗，直流侧电容的动态方程如式（6）所示。

VSC-DC 有功响应的能量完全来自直流侧电容，直流侧输入功率Pin恒定不变，则直流侧电容的线性化方程如式（7）所示。

式中：s为拉普拉斯算子。

VSC-DC 的 控 制 系 统 如 附 录B 图B1 所 示［9］。图中：Pdc(s)、Pq(s)分别为有功、无功控制外环中的比 例-积 分（proportional-integral，PI）控 制 环 节；Pid(s)、Piq(s)分别为有功、无功控制内环中的PI 控制环节；Ppll(s)为PLL 中的PI 控制环节。

PLL 采用d轴端电压定向控制策略，计算公式如式（8）所示。

其线性化方程为：

通过频率控制环节，将PLL 输出的频率ωpll引入有功控制环节中。

忽略电流内环的动态，认为VSC-DC 输出电流能 瞬 间 跟 踪 其 参 考 值，则 有Id=Id，ref、Iq=Iq，ref。由此可得输出电流的线性化方程为：

联立式（5）、式（7）、式（9）、式（11）可得VSC-DC在电压扰动下的传递函数模型，如附录B 图B2所示。

在PLL 坐标系下，节点电压Vpcc∠θpcc的d、q轴分量可被表示为：

通常θpcc与θpll相差很小，线性化式（12）可得：

联立式（9）和式（13），则扰动输入量ΔVq可用Δθpcc替换。

式中：Gpll(s)为PLL 的传递函数。

稳态时，VSC-DC 输出电流在PLL 坐标系下可被表示为：

通常，VSC-DC 输出电压与节点电压的相位差较 小（通 常 小 于10°）［24］，可 认 为Vcq0-Vq0≈0、Vcd0≈Vc0，则式（15）可简化为：

附录B 图B2 中有功环节的电压幅值扰动、无功环节的电压相位扰动可以忽略，认为VSC-DC 有功和无功环节是解耦的。基于此，结合附录B 图B2、式（14）和式（16）可以推导得到VSC-DC 在相位扰动下的传递函数模型，如附录B 图B3 所示，由梅森增益公式［25］可得其传递函数如式（17）所示。

2.2 VSC-AP 的传递函数模型

VSC-AP 的 控 制 系 统 如 附 录B 图B4 所 示［10］。图中：Pp(s)为有功控制外环中的PI 控制环节。具体推导过程与2.1 节相似，区别之处在于控制目标不同。

定有功功率控制下，附加频率控制的动态方程可写为：

VSC-AP 有功电流的线性化方程如式（19）所示，其中，比例增益Kp(s)=Kps+Kd。

以同样的方式可以推导得到VSC-AP 在相位扰动下的传递函数模型，如附录B 图B5 所示，由梅森增益公式可得其传递函数为：

3 并网换流器的动态惯量及其量化评估方法

3.1 并网换流器的动态惯量

结合式（2）、式（3）、式（17）和式（20），可得到附加频率控制下并网换流器的等效传递函数模型，如图2 所示。图中：Hc，dc(p)、Dc，dc(p)分别为并网换流器的设计惯量、阻尼，即传统惯量评估方法下的惯量、阻尼常数。相位扰动下，并网换流器的功率变化量由两 部 分 组 成，即ΔP1和ΔP2。ΔP1为 路 径G1，dc(p)(s)对应的功率响应量，表示未考虑附加频率控制时并网换流器固有的功率响应；ΔP2为路径G2，dc(p)(s)对应的功率响应量，表示考虑附加频率控制后并网换流器新增的功率响应。

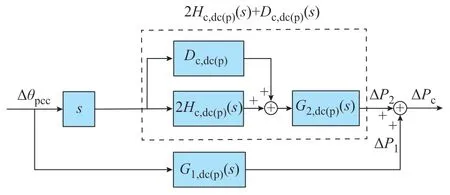
图2 并网换流器的等效传递函数模型Fig.2 Equivalent transfer function model of gridconnected converter

1）G1，dc(p)(s)及其功率响应ΔP1

对于文中控制目标不同的两类并网换流器，G1，dc(p)(s)分别为：

式中：下标“dc”表示传递函数对应于VSC-DC；下标“p”表示传递函数对应于VSC-AP。

如附录C 图C1 所示，传递函数G1，dc(p)(s)的响应机理可通过电压矢量在PLL 坐标系下的变化来解释［26］。在理想情况下，Gpll(s)=1，PLL 的d轴时刻锁定节点电压Vpcc。当Vpcc变化时，并网换流器的输出电压Vc与其相对位置保持不变，如附录C 图C1（a）所示，忽略幅值变化的影响，ΔP1=0。但如果PLL 的锁定速度很慢，甚至Gpll(s)=0，则Vc的相位只由有功环节决定。Vc的动态过程如附录C图C1（b）所示，其响应越慢，ΔP1越大。

基于上述分析，并网换流器的输出电压相位取决于PLL 和有功环节，只有当这两个回路动态过程都减慢时，才能实现较明显的功率响应。此外，随着两者动态过程的结束，并网换流器的输出功率恢复到原有值，ΔP1最终为0。

2）G2，dc(p)(s)及其功率响应ΔP2

如图2 所示，引入附加频率控制后，受控制器动态的影响，并网换流器的动态惯量和阻尼计算公式如式（22）所示。

对于两类并网换流器，G2，dc(p)(s)分别为：

式中：KP，dc、KI，dc分别为Pdc(s)中的比例、积分系数；KP，p、KI，p分别为Pp(s)中的比例、积分系数。

由图2 和式（22）可知，相位扰动发生后，并网换流器中PLL、有功环节和频率控制环节均会参与功率响应，且为并联关系。其中，PLL 提供节点电压的频率扰动信号，频率控制环节根据频率变化改变有功外环的参考信号，有功环节实现参考信号到实际信号的控制过程。因此，并网换流器的动态惯量既取决于其惯量设计参数，又受到控制器中有功环节和PLL 动态的影响，为时变的传递函数。与ΔP2不同，ΔP1响应的是PLL 输出相位与节点电压相位的差值，考虑到PLL 快速的锁相能力，这一差值极小且在扰动期间会迅速衰减为零，可以忽略。

3.2 并网换流器动态惯量的量化评估

3.2.1 并网换流器动态惯量的量化评估方法

对于任意一个一般化的高阶传递函数f(s)有：

式中：ai为常数项系数；n为阶数。

式（24）作为特征方程的解，即系统的特征值，假 设 特 征 值λi=-εi+jωi是f(s)=0 的 第i个 解，其中，εi为实部，ωi为虚部，则必然存在：

考虑到s=λi对于上述系统恒成立，其中，系统的高阶部分fhd(s)=an sn+an-1sn-1+…+a2s2在λi主导的动态特性下可坍缩为一个一阶系统feq(s)，即：

显 然，对 于λi，存 在feq(λi)=fhd(λi)。若 此 时λi为系统的主导特征模态，则一个高阶系统可用一个低阶系统等效替代，两者在主导特征模态λi下的动态特性完全相同。

类似地，交流系统的低频动态特性通常由一个主导特征模态决定。因此，上述等效方法可完全适用。假设交流系统的主导特征模态λd为λd=-εd+jωd，其中，εd、ωd分别为其实部和虚部，将其代入并网换流器动态惯量和阻尼的传递函数表达式，类比于式（26）可得：

式中：Hc，dc(p)，λd、Dc，dc(p)，λd分别为利用系统主导特征模态量化得到的惯量、阻尼；εg、ωg分别为传递函数特征模态λg的实部、虚部。

3.2.2 有功控制外环参数对并网换流器惯量的影响分析

PLL 要快速锁定电网频率，并提供给频率控制环 节，其PI 控 制 器 参 数KP，pll、KI，pll远大于εd、ωd。因此，Gpll(s)|s=λd≈1。对于两类并网换流器，Hc，dc(p)，λd和Dc，dc(p)，λd的具体表达式分别如附录C 式（C1）和式（C2）所示。考虑到εd≪ωd，则可简化为：

1）KP，dc、KI，dc变化对VSC-DC 惯量的影响

将Hc，dc，λd分别对KP，dc、KI，dc求导，可得：

令JP，dc=2Hv-KI，dc，JI，dc=K-K-4。由 式（29）可 知，KP，dc和KI，dc变 化 对VSCDC 惯 量 的 影 响 分 别 取 决 于JP，dc和JI，dc的 正 负。对 于KP，dc来 说，当JP，dc＜0 时，KP，dc增 大 将 使 惯 量 减 小，反 之 亦 然。对 于KI，dc来 说，当JI，dc=0 时 惯 量 最 大。若 此 时KI，dc增 大 将 使JI，dc＜0，惯 量 减 小；若 此 时KI，dc减小将使JI，dc＞0，惯量减小。

2）KP，p、KI，p变化对VSC-AP 惯量的影响

将Hc，p，λd分别对KP，p、KI，p求导，可得：

令JP，p=dHc，p，λd/dKP，p、JI，p=dHc，p，λd/dKI，p。由式（30）可知，对于JP，p来说，当JP，p=0 时，惯量最小。若此时KP，p增大将使JP，p＞0，惯量增大；若此时KP，p减 小 将 使JP，p＜0，惯 量 增 大。对 于KI，p来 说，当JI，p=0 时，惯量最小。若此时KI，p增大将使JI，p＞0，惯 量 增 大；若 此 时KI，p减 小 将 使JI，p＜0，惯 量 增 大。此外，由式（28）可知，Hc，p，λd＜Hc，p。

3.2.3 系统主导特征模态对并网换流器惯量的影响分析

将Hc，dc，λd、Hc，p，λd分别对ωd求导，可得：

令Jλd，dc=dHc，dc，λd/dωd、Jλd，p=Dc，p(K+2KP，p+1)-Hc，pKI，p(KP，p+1)。通 常Hv、KP，dc远小于KI，dc。对于VSC-DC 来 说，当ωd较小时，Jλd，dc＞0，惯量随着ωd增 大 而 增 大；当ωd不 断 增 大 使 得Jλd，dc＜0 时，惯量随着ωd增大而减小。因此，当Jλd，dc=0 时惯量最大。对于VSC-AP 来说，当Jλd，p＜0 时，ωd增大将使惯量减小，反之亦然。

由上述分析可知，并网换流器惯量的变化趋势受多种参数的共同影响，较为复杂。附录C 表C1 列出了主要影响因素从零增大时，两类换流器惯量的一般变化趋势。

4 算例与仿真验证

4.1 并网换流器传递函数模型验证

本节基于MATLAB/Simulink 搭建了与图1 一致的单并网换流器并网系统，参数见附录D 表D1。在0.1 s 时向系统施加阶跃扰动，使θpcc下降3°。

附录D 图D1（a）分别对比了VSC-DC 在有、无频率控制时的时域仿真结果。可以看出，相比于附加频率控制，并网换流器固有的有功响应非常微弱可忽略不计，与3.1 节中的分析结果一致。此外，图中附加频率控制下基于VSC-DC 传递函数模型的仿真结果与基于Simulink 的时域仿真结果基本一致。类似地，附录D 图D1（b）分别对比了VSC-AP在有、无频率控制时的时域仿真结果，验证了本文构建模型的准确性。

4.2 并网换流器动态惯量的量化评估方法验证

本节基于MATLAB/Simulink 搭建了如附录D图D2 所示的两机测试系统。图中：G1 为200 MW的同步发电机，带有调速器和励磁控制系统，详细参数见附录D 表D2。为更清楚反映VSC 惯量变化对系统频率响应（system frequency response，SFR）的影响，G2 与G1 容量相同，以消除容量不同带来的影响，G2 由100 台相同的2 MW 的VSC 聚合而成，总额定功率为200 MW。负荷A（200 MW+j15 Mvar）为正常状态下的系统负荷，负荷B（17 MW）为第1 s时投入系统的扰动负荷ΔPl。与之对应地，建立了SFR 模 型，如 附 录D 图D3 所 示。图 中：R为 等 效 调差系数；Ggov(s)为调速器的传递函数，具体表达式如附录D 式（D1）所示。G1 采用了文献［27］中所提出的等效降阶模型，G2 采用了图2 中的等效传递函数模型。

基于上述系统，本节设置了系统参数、运行工况不同的2 个算例：算例1 为原系统，G1 有功功率工作点为0.3 p.u.，G2 并网节点电压工作点为1 p.u.；算例2 中G1 有 功 功 率 工 作 点 为0.5 p.u.，G2 并 网 节 点电压工作点为0.8 p.u.，G1 阻尼系数为1 p.u.，频率控制中Kdc为55.56 p.u.，Kp为2 p.u.，Kd为4 p.u.。

在不同系统特性下，2 个算例分别采用本文量化评估方法和传统惯量评估方法得到的并网换流器惯量如附录D 表D3 所示。图3 分别对比了算例1、算例2 中双机系统时域仿真和SFR 模型仿真的频率响应。可以看出，扰动发生后，区别于采用传统评估惯量的SFR 模型响应结果，采用本文量化惯量的SFR 模型响应结果与时域仿真模型响应结果更加吻合。

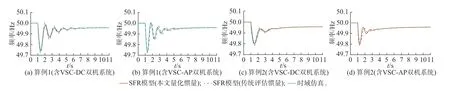
图3 动态惯量量化评估方法的验证Fig.3 Verification of quantitative evaluation method for dynamic inertia

表1 对应给出了图3 中频率响应的特征指标计算结果，其中，相对误差均以时域仿真为基准，计算平均变化率的时间段约为扰动后300 ms。相较于采用传统评估惯量，采用量化惯量所得指标计算结果与时域仿真结果更接近，其相对误差均小于5%。上述结果验证了动态惯量量化评估方法的准确性，且基于此方法所得频率特征的精度满足工程需要。

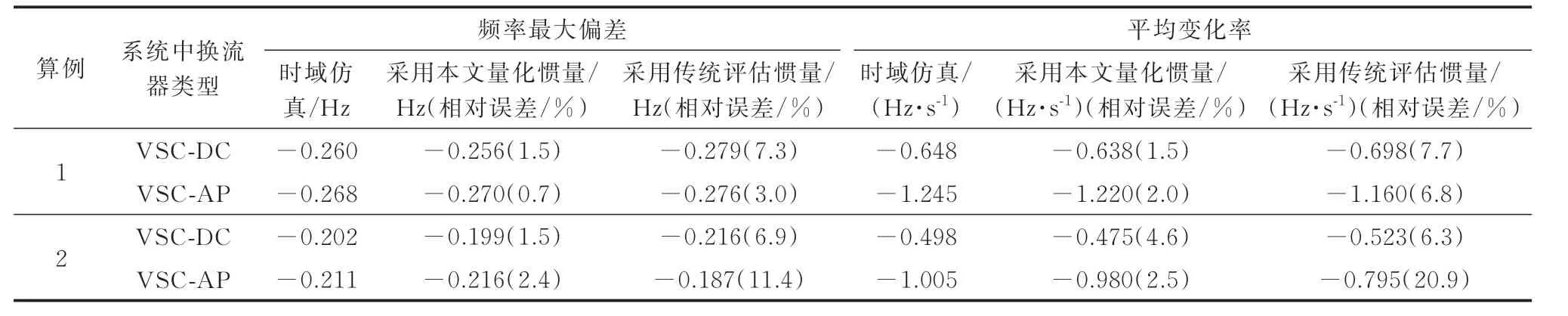
表1 SFR 的特征指标计算结果Table 1 Calculation results of characteristic indices of SFR

4.3 并网换流器惯量的影响因素及规律

图4 和附录E 图E1 中分别给出了VSC-DC 和VSC-AP 在不同主导特征模态下的惯量变化轨迹。图中：主导特征模态实部-εd、虚部ωd的变化范围分别为（-1，0） rad/s、（0，15） rad/s。本文中，比例系数单位均为p.u.，积分系数单位均为rad/s。灰色平面为VSC-DC 和VSC-AP 的设计惯量，彩色平面为本文所量化的动态惯量，其颜色越浅惯量越大。

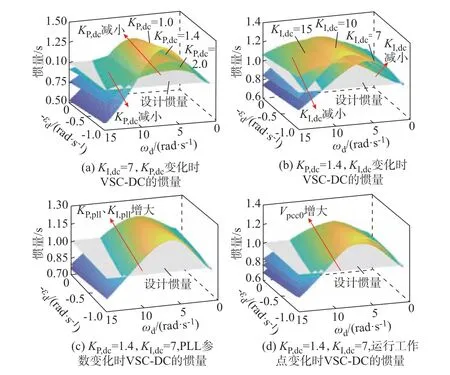
图4 控制器参数和运行工作点对VSC-DC 惯量的影响Fig.4 Impact of controller parameters and operation points on inertia of VSC-DC

4.3.1 VSC-DC 有功控制外环参数

图4（a）中，KI，dc=7，KP，dc分 别 取1.0、1.4、2.0。由式（29）可知，JP，dc=0 时，KP，dc变化不会导致惯量改变，此时计算得到ωd=9.86 rad/s，这与图中3 个平面的交点基本一致。当ωd＜9.86 rad/s 时，图中惯量随着KP，dc减小而单调递增；ωd＞9.86 rad/s 时，惯 量 随 着KP，dc减 小 而 单 调 减 小。与 分 析 一 致，KP，dc对惯量的影响取决于系统主导特征模态频率，呈单调 关 系。频 率 较 小 且JP，dc＞0 时，增 大KP，dc可 增 大惯量，此时系统的设计惯量偏向保守，反之则会出现设计惯量不足的问题。

图4（b）中，KP，dc=1.4，KI，dc分 别 取7、10、15。可 以 看 出，ωd较 小 时，JI，dc＜0，KI，dc减 小 使 惯 量 增大，同 时JI，dc增 大 接 近 于0；ωd较 大 时JI，dc＞0，KI，dc增大使惯量增大，同时JI，dc减小接近于0。因此，当系统主导特征模态一定时，调节KI，dc不断接近JI，dc=0 时，可增大并网换流器的惯量。

4.3.2 VSC-AP 有功控制外环参数

附 录E 图E1（a）中，KI，p=10，KP，p分 别 取0.7、1.4、2.0。可以看出，ωd较小时，JP，p＜0，KP，p增大使惯 量 减 小，同 时JP，p增 大 接 近 于0；ωd较 大 时JP，p＞0，KP，p减小使惯量减小，同时JP，p减小接近于0。因此，在惯量设计时应尽量避免JP，p=0 这一情况。

附 录E 图E1（b）中，KP，p=0.7，KI，p分 别 取10、15、20。可以看出，在图中主导特征模态的变化范围 内JI，p＞0，KI，p增 大 使 惯 量 增 大，同 时JI，p减 小 接近于0。因此，在惯量设计时应尽量避免JI，p=0 这一情况，且可将上述两种情况下惯量的最小值作为VSC-AP 最保守的惯量，用于系统的频率稳定性分析中。此外，与式（28）一致，图中VSC-AP 的惯量恒小于设计惯量，意味着VSC-AP 的设计惯量应大于实际需求惯量。

4.3.3 其他环节因素

1）PLL 参数

设置PLL 参数KP，pll分别为30、50、70，KI，pll对应为1 500、2 000、2 500，其VSC-DC 和VSC-AP 的惯量变化轨迹分别如图4（c）和附录E 图E1（c）所示。与分析一致，由于KP，pll、KI，pll均远大于εd、ωd，其变化对惯量的影响很小，可忽略。

2）运行工作点

设置并网换流器节点电压幅值Vpcc0分别为0.8、1.0、1.2 p.u.，VSC-DC 和VSC-AP 的惯量变化轨迹分别如图4（d）和附录E 图E1（d）所示。可以看出，运行工作点变化对惯量的影响很小，可忽略。

3）系统动态特性

由图4 和附录E 图E1 可知，并网换流器的惯量受到交流系统动态特性的显著影响。对于VSC-DC来说，系统主导特征模态的频率从零增大时，惯量先增大再降低。因此，惯量与振荡频率呈现非单调关系，Jλd，dc=0 时 存 在 最 大 值。对 于VSC-AP 来 说，Jλd，p＜0 时，主 导 振 荡 模 式 的 频 率 增 大 将 使 惯 量 减小，反之亦然。因此，惯量与振荡频率呈现单调关系。此外，当振荡频率较低时，两类换流器惯量和设计惯量接近，可忽略控制器的动态过程。

一般主导模式阻尼都较小，相比频率的变化较微弱，其影响可忽略。

4.3.4 惯量分析结果的时域仿真验证

图5 为不同有功控制外环参数下双机的SFR。基于本文的分析结论，设置有功控制外环参数的调节方法。附录E 表E1 和附录E 表E2 分别给出了不同有功控制外环参数下两类并网换流器的量化惯量和阻尼。其中，VSC-DC 和VSC-AP 原有的设计惯量分别为1 和0.5。可以看出，有功控制外环参数变化对系统主导特征模态频率的影响很微弱，可忽略。

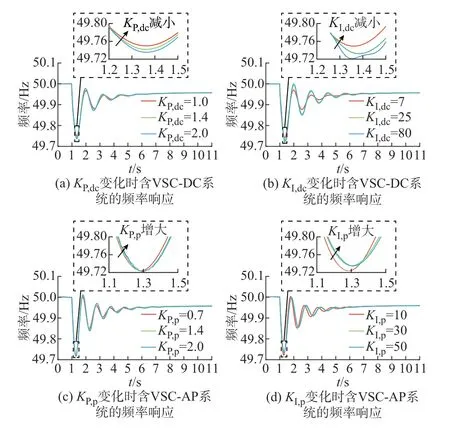
图5 不同有功控制外环参数下的SFRFig.5 SFR under different active outer loop parameters

由附录E 表E1 可知，含VSC-DC 双机系统主导特 征 模 态 的 频 率 约 为5 Hz。 当KI，dc=7 时，JP，dc＜0，减小KP，dc使惯量增大；当KP，dc=1.4 时，令JI，dc=0，可 得KI，dc=6.76，减 小KI，dc使 其 接 近 于6.76，惯量将增大。

由附录E 表E2 可知，含VSC-AP 双机系统主导特 征 模 态 的 频 率 约 为6.4 Hz。当KI，p=10 时，令JP，p=0，可 得KP，p=0.14，增 大KP，p使 其 大 于0.14，惯 量 增 大。当KP，p=0.7 时，令JI，p=0 可 得KI，p=1.66，增大KI，p使其大于1.66，惯量将增大。

对于含VSC 双机系统来说，SFR 初期的频率变化率主要由系统惯量决定，系统惯量越大，系统频率变化率越小。图5（a）、（b）分别为KP，dc、KI，dc变化时含VSC-DC 双机的SFR。可以看出，KP，dc、KI，dc减小时，响应初期的频率变化率减小。这和附录E表E1 中KP，dc、KI，dc减 小 时VSC-DC 惯 量 增 大 的趋势一致，仿真结果与理论分析结论吻合。类似地，图5（c）、（d）分别为KP，p和KI，p变化时，含VSCAP 双 机 的SFR。可 以 看 出，KP，p和KI，p增 大 时，响应初期的频率变化率更小。这和附录E 表E2 中KP，p、KI，p增 大 时VSC-AP 惯 量 增 大 的 趋 势 一 致，验证了理论分析结论的正确性。

5 结语

本文针对定直流电压控制和定有功功率控制这两类主流的控制方式，分别推导了附加频率控制下并网换流器的传递函数模型，并基于系统主导特征模态量化评估了其动态惯量，分析了多种因素与并网换流器惯量间的映射关系及影响规律。主要结论如下：

1）附加频率控制下，并网换流器惯量既与设计参数有关，又受到控制器中有功控制环节的影响，为时变的传递函数，意味着系统特性也会影响并网换流器在频率扰动期间所提供的惯量。与附加频率控制相比，并网换流器固有的有功响应非常微弱，可忽略不计。

2）利用系统主导特征模态可以较为准确地量化评估并网换流器的动态惯量，且能够反映控制参数、运行工况和系统特性等不同因素对惯量的影响机制。在这些参数正常变化的范围内，有功控制外环参数会显著改变并网换流器原有的设计惯量。但是，PLL 参数和运行工况对惯量的影响较小，可以忽略。

3）对于定直流电压控制的并网换流器，定直流电压外环的比例系数与惯量呈单调关系，可根据单调关系来增大或减小惯量。而积分系数与惯量呈非线性关系，惯量存在最大值，惯量设计时应尽量满足这一条件。对于定有功功率控制的并网换流器，定有功功率外环的比例系数和积分系数均与惯量呈非线性关系，惯量存在最小值，惯量设计时应尽量避免这种情况，且两者中的最小值可作为并网换流器最保守的惯量用于系统频率稳定性分析中。

本文仅通过仿真验证了所提方法和分析结论的有效性，未来将开展实验验证，并在所提动态惯量量化评估方法的基础上，进一步研究构网型虚拟同步发电机控制下并网换流器的惯量响应特性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。