考虑频率空间分布特性的虚拟惯量配置优化

2024-04-30刘瑞煦吴佳良赵天阳

电力系统自动化 2024年8期

刘瑞煦，汪震，吴佳良，赵天阳，单煜

（1.浙江大学电气工程学院，浙江省杭州市 310027；2.瑞典皇家理工学院电气工程与计算机科学学院，斯德哥尔摩 11428，瑞典）

0 引言

频率稳定是电力系统安全稳定运行的基本要求。然而，大规模基于电力电子设备的新能源接入改变了电力系统的频率动态特性，同时，其出力不确定性、低惯量等问题使电力系统频率稳定性进一步恶化［1］。为避免频率失稳，国家能源局印发的《电力辅助服务管理办法》［2］对新型电力系统中包括电力电子设备在内的并网主体提出了提供惯量支撑服务的需求。以虚拟同步机（virtual synchronous generator，VSG）［3］为代表的电力电子调频控制可以主动响应系统频率变化，同时提供虚拟惯量支撑，是缓解新型电力系统频率问题的有效手段之一。但基于电力电子接口的新能源发电特性与传统电源不同，所提供的虚拟惯量灵活可控，使得务节点的频率动态特性异质化明显，加剧了惯量以及频率的时空分布差异化，对系统频率分析、控制与保护产生了显著影响。因此，为保障新型电力系统频率安全，需进一步考虑新型电力系统频率空间特性约束，研究电力电子设备虚拟惯量配置问题。

传统电力系统因惯量充足，频率变化相对较慢，往往忽略频率空间分布差异化，可将系统简化为单节点系统，采用单机转子运动方程［4］描述系统频率动态，根据等效单机系统的频率指标衡量系统稳定性。基于惯量中心（center of inertia，COI）假设，将所有发电机惯量集中于等效COI，用系统惯量之和作为量化系统频率抗扰动能力的指标之一，并通过提升系统惯量水平改善频率稳定性［5］。然而，高比例电力电子设备并网使电力系统频率空间分布不均现象日益凸显，传统基于COI 的频率分析方法不再适用。

针对频率空间分布差异化的分析，目前主要有时域仿真、人工智能、模型分析等频率响应分析方法［1］。其中，时域仿真法计算精度高但计算复杂；依赖于大数据训练的人工智能法通用性较差；而模型分析法计算复杂度低且泛化能力强，有利于频率动态与系统参数的解析关系量化。文献［6］提出的“分频器”理论可以基于电源设备调频特性与电网结构推导系统中务节点的频率动态，是分析频率空间分布差异化的有效工具。

系统频率响应分析的目的是得到频率稳定性评估指标，进而指导系统规划、运行与控制设计。目前，存在时域、频域以及能量域等不同视角下的频率稳定性评估指标。其中，时域指标以频率最低点与频率变化率（rate of change of frequency，RoCoF）为代表；频域上可利用系统传递函数的范数量化系统对频率扰动的抑制能力［7］。从能量域角度看，频率波动的本质是功率不平衡，频率偏移对时间的积分可以描述频率动态过程中不平衡功率的累积效应［8-9］，即能量不平衡；此外，传统电力系统中同步发电机（synchronous generator，SG）转子动能变化也可直接反映频率变化情况［10］。基于能量考虑的频率安全量化指标一般具有清晰的物理含义，但当前能量域频率指标均无法体现新型电力系统惯量以及频率空间分布差异化的问题。

新型电力系统频率稳定性提升可以从系统运行调度和保护控制等方面展开。优化虚拟惯量参数是改善VSG 调频性能的一种方式，同时，惯量空间分布亦影响系统频率响应动态特性［11］，如何优化分布式能源的虚拟惯量配置以提升系统频率稳定性有待深入研究。文献［12-13］从提升系统小干扰稳定性角度出发，以优化系统阻尼比为目标研究虚拟惯量分配问题，但其仅以系统最低惯量需求为限制，没有考虑频率暂态稳定等约束。文献［14-17］通过改善频率相关的系统暂态能量指标配置虚拟惯量，但无法保证局部频率响应满足要求。文献［18］以系统运行经济效益最大为目标配置储能系统虚拟惯量，并且考虑了务区域频率最低点、RoCoF 约束对务自区域虚拟惯量设置的限制，但其无法体现系统务节点的频率动态响应特性。

为适应新型电力系统新的频率特性，本文提出了一种考虑系统频率响应空间分布差异化的虚拟惯量优化方法。基于“分频器”理论，建立能反映全网务节点频率动态的系统频率响应模型；进一步，提出节点惯量与节点动能指标，量化频率空间响应性能；然后，以优化频率动态过程中节点动能指标为目标，配置虚拟惯量，提高全系统务节点频率稳定性；最后，通过算例仿真分别就节点惯量分布特性以及所提虚拟惯量优化模型的有效性进行验证。

1 系统频率响应建模

考虑一个N节点的系统，系统由NG个电源节点、NL个负荷节点以及网络B 组成，NG+NL=N。本文重点研究系统频率响应问题，故电源节点主要指可自主控制自身频率的设备（如SG、采用VSG 控制的组网型变流器）主导的节点，负荷节点指不具备主动控制自身频率能力的节点。

电源节点设备可以自主控制自身频率，满足摇摆方程（标幺制），如下所示：

式中：ω0为基准频率；δG，i、ωG，i、PM，i、PE，i、HG，i、DG，i分别表示节点i处电源设备的相角、频率、输入的机械功率、输出的电磁功率、转子的惯性时间常数或VSG 虚拟惯量、阻尼系数。

另外，考虑到系统频率一次调整响应，用式（2）反映电源设备的有功调节［19］，表示SG 的原动机调速器动态［20］或电力电子设备的一次调频动态［21］，通过设备时间响应常数进行区分。

式中：Ts，i、DP，i、P分别为节点i处设备的响应时间常数、下垂系数、机械功率的参考值。

采用式（1）与式（2）表示电源节点设备的频率响应特性。需说明的是，文中以电力电子设备采用VSG 控制为例，对于其他调频控制可以通过拟合摇摆方程的方式［18］进行类似的频率响应分析。

系统务节点通过输电线路相连，根据电源与负荷节点的划分，将系统网络矩阵分为4 个子矩阵［6］，忽略线路电阻，得到重新排布后的节点电纳矩阵B，如下所示：

式中：BGG∈RNG×NG，BGL∈RNG×NL，BLG∈RNL×NG，BLL∈RNL×NL。

假设务节点电压恒定且等于额定值、线路电阻远小于电抗值以及sinδ≈δ，采用直流模型［22］表示电磁功率输出（对节点而言为注入功率），即

式中：PE=[PE，1，PE，2，…，PE，NG]T为电源输出功率向量；δG=[δG，1，δG，2，…，δG，NG]T和δL=[δL，1，δL，2，…，δL，NL]T分别为电源输出功率和负荷节点输出功率对应的相角向量。

负荷节点的输出功率类似，表示如下：

式中：PL=[PL，1，PL，2，…，PL，NL]T为负荷节点输出功率向量。

参考Kron 化简［23］思想，仅保留电源节点上的动态，消去负荷节点变量，将负荷节点上发生的功率扰动等效分配到电源节点（需要注意的是，本文在负荷节点中增加了一个虚拟节点，以降低模型对地支路简化过程中的误差［23］）。结合式（1）、式（2）、式（4）及式（5），可得如下务电源节点频率响应模型：

式中：BR为化简网络电纳矩阵；为电源节点处等效负荷向量；TGL为功率分配矩阵，TGL∈RNG×NL；PM=[PM，1，PM，2，…，PM，NG]T为电源节点处机械功率输入向量；P=[P，P，…，P]T为电源节点处机械功率输入参考值向量；ωG=[ωG，1，ωG，2，…，ωG，NG]T为电源节点频率矩阵；ω0=diag(ω0)、HG=diag(HG，i)、DG=diag(DG，i)、DP=diag(DP，i)、Ts=diag(Ts，i)分别为基准频率、惯量时间常数、阻尼系数、下垂系数以及时间常数构成的对角矩阵；I=[1，1，…，1]为NG维单位列向量。

根据文献［6］，负荷节点的频率可认为是电源节点频率关于网络拓扑的加权叠加，即

式中：ωL为负荷节点频率矩阵；TLG为与网络拓扑相关的频率加权矩阵，TLG∈RNL×NG，TLG=-BBLG=T。

综上，利用式（6）与式（10）可以分析全网所有节点频率动态响应，进而表征系统频率空间分布特性。

2 节点频率响应评估

考虑到频率的空间分布特性，本章就系统节点表现出的频率响应性能进行分析，提出节点惯量指标以及节点动能偏差指标，用于定量刻画局部节点的抗频率扰动能力与频率动态响应性能。

2.1 节点惯量指标

2.1.1 节点惯量定义

物理学中，惯量是对物体惯性大小的量化，即表示物体抵抗运动状态变化的能力［24］。电力系统的惯量表现为抑制外在扰动引发的频率变化的能力，系统功率不平衡、扰动发生瞬间的频率变化以及惯性时间常数满足如下表达式：

式中：ωsys、ΔPsys分别为系统频率和功率不平衡量；Hsys为系统等效惯性时间常数。

上述表达式是系统角度的动态响应，事实上，电网中不同节点上的频率变化情况并不同，反映出的不同节点对扰动抑制能力也不同。根据摇摆方程，定义节点上功率扰动与初始RoCoF 两倍的比值为节点惯量，作为评估节点上扰动抑制能力的指标，如下所示：

式中：Hi为节点i处惯量；ΔPL，i为节点i处功率扰动；ωi为节点i处频率。

2.1.2 节点RoCoF

忽略频率变化对传输线路、变压器、负荷以及发电机参数的影响，对式（10）求微分可得负荷节点RoCoF，如下所示：

根据式（13）可知，负荷节点RoCoF 与网络拓扑以及电源节点RoCoF 有关。而电源节点最大RoCoF 可以利用扰动初始时刻的功率不平衡以及电源节点上对应的设备惯量估计。负荷扰动发生瞬间，电源承担的不平衡功率满足功率分配系数［25］，如式（8）所示，其他典型的扰动如线路切换、发电机扰动等也可得到类似的功率不平衡分配表达［26］。

以负荷扰动为例，根据电源节点摇摆方程式（6），忽略扰动发生瞬间电源的机械功率变化及相角变化，可得电源节点RoCoF 如下：

式中：ΔPL=[ΔPL，1，ΔPL，2，…，ΔPL，NL]T表示负荷节点功率扰动向量。

结合式（13）与式（14），可得负荷节点RoCoF如下：

由式（15）可以看出，负荷节点RoCoF 与电源节点惯量配置、网络拓扑以及扰动相关。因此，不同的虚拟惯量配置会影响频率空间分布特性。

2.1.3 节点惯量指标定义

根据式（12）与式（15），假设节点i处发生大小为ΔPL，i的功率扰动，将节点RoCoF 代入式（12），消去公共扰动项，可以得到仅与电源节点处设备惯量大小以及网络拓扑有关的节点i的节点惯量指标Hi，如式（16）所示。Hi可用于衡量节点抵抗频率变化的能力，即反映其惯性响应阶段的频率稳定性。

式中：TLG，ij表示加权矩阵TLG中第i行第j列对应的元素；HG，j表示节点j处电源的惯量。

2.2 节点动能偏差指标

从能量角度看，频率波动的本质是功率不平衡。传统电力系统中，SG 转子存储的动能变化可以反映系统频率变化［22］，其动能变化源于不平衡功率的累积效应，转子动能表达式如下：

式中：K表示SG 转子储存的动能；HSG为SG 转动惯量；ω为转子转速。

为了体现频率空间分布差异，借鉴上述概念，结合节点惯量与节点频率定义节点动能。进一步，定义当前时刻动能与基准频率下动能偏差绝对值为节点动能偏差Ki，即

该指标可以一定程度上反映系统频率与能量的变化，同时反映务节点的频率响应特性。另外，在系统其他条件一定的情况下，惯量越大，惯量控制成本越高，在惯量响应初始阶段的惯量支撑功率越大，但是相对应的RoCoF 与频率偏差小，系统频率稳定提升；反之，惯量成本降低，但频率稳定性相对较差。因此，节点动能偏差指标可以用于协调惯量支撑成本与频率稳定之间的关系。

3 虚拟惯量优化配置模型构建

高比例电力电子设备并网使电力系统频率空间分布不均的现象日益凸显，而系统惯量配置直接影响了系统频率空间响应特性。因此，本文考虑频率空间分布差异化，结合上述系统频率响应模型及节点频率响应评估指标，针对电力电子变流器高占比电力系统构建虚拟惯量优化配置模型，包括基于节点动能的优化目标函数、考虑系统/节点/设备的安全稳定运行的约束条件以及优化求解流程。

3.1 目标函数

考虑频率空间分布特性，以扰动发生后系统务节点中最大动能偏差累积量最小为目标，表达式如下：

式中：Tf为惯性响应时间。

Hi可反映务电源针对节点i的综合出力情况，而频率偏差体现节点频率响应特性，故该指标可实现调频过程中惯量支撑成本与频率稳定之间的权衡。

3.2 约束条件

针对虚拟惯量配置问题，本文主要考虑了频率最低点、RoCoF、调频容量限幅等约束，分别从系统惯量需求、节点频率稳定性以及设备容量限制3 个层面探讨基于VSG 实现的虚拟惯量优化配置约束条件。

3.2.1 系统约束

系统约束主要从系统级最低惯量需求角度进行考虑。通过电源惯量的加权平均得到系统的COI频率［4］，用于分析全局的频率响应特性，如下所示：

式中：ωCOI为COI 频率。

本文根据澳大利亚能源市场委员会关于最低惯量需求的估计［27］，综合考虑最大有功扰动下RoCoF限制以及惯量最大的SG 切除的影响，确定保证系统安全运行的最低惯量水平。系统频率响应过程中，最大的RoCoF 一般出现在扰动发生瞬间，此时一次调频等功能尚未响应，故可以忽略这一阶段（惯性响应阶段）中慢动态变化量，得到频率变化初期（t→0+）的RoCoF 表达式，其应小于允许的最大RoCoF，如下所示：

式中：δoF为系统最大RoCoF；δoF表示允许的最大RoCoF；ΔP（0+）表示扰动瞬间全局有功不平衡量。

另外，考虑到最大惯量机组切除的极端情况，系统所需的安全运行惯量H应满足式（22），对应到电力电子设备需要提供的最小虚拟惯量Hmin如式（23）所示。

式中：Hloss表示最大惯量机组的惯性时间常数；NSG、NVSG分别为SG 与电力电子设备对应节点的数量；HSG，j、HVSG，i分别为节点j处SG 与节点i处电力电子设备提供的惯量。

3.2.2 节点约束

由频率稳定性指标（如频率最低点或RoCoF）触发的保护装置安装在特定母线上，而COI 频率并不对应系统中任一节点频率，并且考虑到新型电力系统频率空间分布差异化明显，即使COI 频率满足约束也无法保证系统某些节点的频率在规定范围内［26］。因此，为保证系统安全稳定运行，本文考虑了系统务节点的频率以及RoCoF 约束，如下所示：

式中：i=1，2，…，N；ω和ω分别为频率限制的上、下界；δRoCoF，i为节点i处RoCoF。

3.2.3 设备约束

忽略调频过程中新能源出力波动，设备方面主要考虑电力电子设备调频限幅，以避免电力电子设备留有过多有功备用，影响其运行经济性，表达式如下：

另外，考虑务VSG 虚拟惯量参数设置的上下界可得：

式中：H，i和H，i分别为务VSG 虚拟惯量参数的上、下界。

3.3 虚拟惯量优化配置模型

综上所述，考虑频率空间分布特性的虚拟惯量优化配置模型如下：

式（28）构成了虚拟惯量优化配置模型。考虑频率空间分布特性，用电源节点频率响应常微分方程组与负荷节点频率响应代数方程共同构成描述系统频率响应动态的微分-代数方程组；基于节点惯量以及节点动能偏差指标，以系统扰动后最大节点动能偏差累积量最小为目标，同时考虑系统惯量、节点频率及设备稳定等约束，对不同VSG 的虚拟惯量系数进行优化配置，在保证系统全局与局部的频率稳定性的同时，减少惯量支撑成本。

3.4 求解流程

虚拟惯量作为优化变量隐式地包含于优化问题（式（28））中，优化变量与目标函数以及约束条件的显性关系求解困难。因此，采用全局搜索能力强、并行计算快的遗传算法（genetic algorithm，GA）［28］进行求解。基于GA 的虚拟惯量配置优化求解过程如图1 所示。

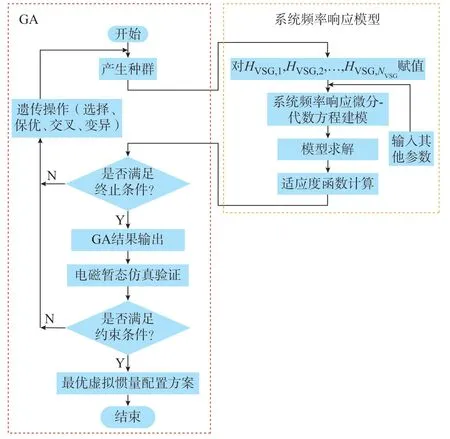
图1 虚拟惯量配置优化设计过程Fig.1 Design process of virtual inertia configuration optimization

具体步骤如下：

步骤1：在式（28）中最后一行约束范围内产生初始种群。

步骤2：将产生的种群赋值并作为系统频率响应模型中的虚拟惯量系数HVSG，i（i=1，2，…，NVSG），根据式（28）中前4 行约束求解系统务节点频率响应动态，并计算适应度函数（式（28）中目标函数）。若频率响应结果不满足约束条件（式（28）中第5 行至第8 行约束式），则在适应度函数中增加惩罚。

步骤3：判断是否满足GA 终止条件（达到最大迭代次数或收敛至稳定解）。若满足，退出GA 并跳转至步骤5；否则，跳转至步骤4。

步骤4：进行遗传操作，产生新的虚拟惯量系数种群，并跳转至步骤2。

步骤5：输出GA 求解结果，进行电磁暂态仿真（建模相关内容见文献［29］），验证系统频率响应是否满足式（28）中第5 行至第8 行约束。若满足，退出求解过程，并得到虚拟惯量配置优化最终结果，否则，跳转至步骤4。

4 仿真验证

为验证所提节点惯量指标与虚拟惯量优化配置模型的有效性，在MATLAB/Simulink 中搭建68 节点仿真系统，如图2 所示。

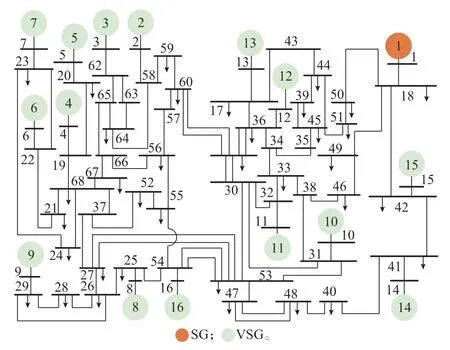
图2 新英格兰16 机68 节点系统结构Fig.2 Structure of New England 16-machine 68-bus system

该系统在新英格兰16 机68 节点系统的基础上修改而成，系统建模与相关参数见文献［29］。算例中，节点1 为SG 节点（设对应惯量时间常数HSG，1=30 s，Ts，1=3 s），节点2～16 均为VSG 节点（Ts，i=0.5 s，i=2，3，…，16），容量均为5 p.u.，算例的优化变量是系统中15 台VSG 的虚拟惯量（HminVSG，i=0.1 s，HmaxVSG，i=60 s，i=2，3，…，16）。假设通过故障预测得到系统中节点56 处存在最大5 p.u.潜在负荷扰动，图3 给出了3 种虚拟惯量配置方案，具体如下。

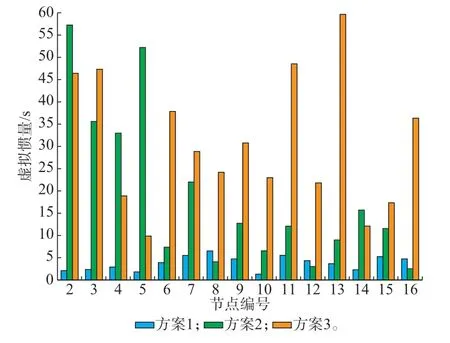
图3 储能系统的虚拟惯量分配方案Fig.3 Virtual inertia allocation scheme for energy storage systems

1）方案1：低惯量水平的随机虚拟惯量配置。

2）方案2：基于广义暂态能量且满足COI 频率约束（式（23）），但未考虑节点频率空间分布特性的虚拟惯量配置（优化目标函数见文献［14-15］）。

3）方案3：基于本文所提虚拟惯量优化配置模型的虚拟惯量配置。

4.1 节点惯量指标验证

为说明所提节点惯量指标可反映负荷节点上的潜在惯性支撑能力，在图3 所示的3 种虚拟惯量配置方案下，对比验证所提节点惯量指标与节点惯量实验值。其中，实验值是通过仿真得到的，具体做法为：以负荷节点1～16 为例，分别对务节点施加扰动，计算式（12）得到节点惯量实验值。通过图4 对比结果可以看出，节点惯量指标与实验值趋势相符，说明节点惯量指标可以定量反映节点抵抗频率变化的能力。

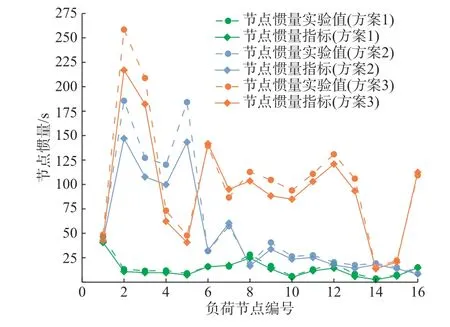
图4 节点惯量指标与实验值对比Fig.4 Comparison of experimental nodal inertia and calculated nodal inertia index

4.2 虚拟惯量优化结果分析

为进一步验证虚拟惯量优化配置模型的有效性，假设节点56 处发生5 p.u.负荷扰动，分别对比了3 种虚拟惯量配置方案下的系统性能表现。3 种虚拟惯量配置方案下的系统惯量空间分布热力图及对应的全节点频率响应曲线如图5 所示。其中，系统惯量空间分布热力图是利用节点惯量指标得到的。

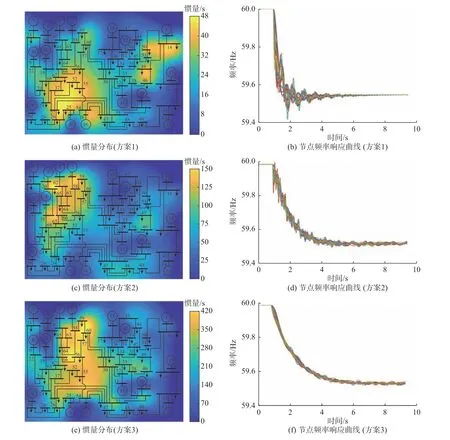
图5 系统惯量分布与频率响应Fig.5 Inertia distribution and frequency response of system

通过图5（a）、（c）与（e）可直接观察到3 种配置方案下系统惯量空间分布情况。其中，在基于本文所提模型的虚拟惯量配置方案3 下，扰动节点56 附近惯量分布较集中、节点惯量指标数值较大，说明方案3对扰动的抑制更为直接且抗扰能力更强。图5（b）、（d）与（f）反映了系统务节点的频率动态响应，通过对比可以看出，虚拟惯量配置方案3 下系统务节点频率波动更小，且系统频率波动空间差异化明显小于其他两种配置方案，同时说明以空间中务节点频率响应指标最大值最小化作为目标函数，可进一步提升系统频率的一致性。

进一步，3 种惯量配置下务节点的最大频率偏差以及RoCoF 如图6 所示。

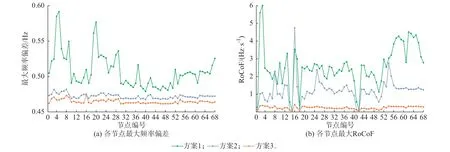
图6 系统各节点频率响应Fig.6 Frequency response of each node in system

图6（a）对比了系统务节点最大频率偏差。在方案1 中系统最大频率偏差较大，且务节点间数值相差较大，体现了系统中务节点频率空间分布差异化；方案2 因考虑了COI 频率相关指标的约束，务节点频率最大变化量相较于方案1 变小；而基于本文虚拟惯量优化模型的方案3 中，务节点最大频率偏差与方案1 和方案2 相比均较小，频率稳定性得到提升。图6（b）对比了系统务节点最大RoCoF。方案1 中，低惯量水平的系统抵抗频率变化能力弱，大部分节点的RoCoF 指标超过限制（1 Hz/s），无法满足频率稳定性要求；方案2 的约束可以保证COI 频率的RoCoF 满足条件，但无法保证局部频率响应指标满足要求，68 个节点中仍有56 个节点的RoCoF超过限制；而基于本文所提惯量优化模型的配置方案3，考虑了频率空间分布特性，保证了所有节点的RoCoF 指标都满足要求，并且务节点频率响应相对一致，系统的频率稳定性得到提升。需要说明的是，在2 种虚拟惯量配置方案下，系统务节点频率稳态偏差均为59.544 Hz，因为在不考虑二次调频的情况下，系统稳态频率偏差主要与扰动大小、一次调频相关参数等相关，不受惯量配置影响。