全功率型风电机组调频控制器的实用化辨识方法

金泳霖，晁璞璞，刘志辉，张 凯，张睿浩，崔浩瀚，李卫星

（大连理工大学电气工程学院，辽宁省大连市 116024）

0 引言

近年来，随着新能源占比的提升和高压直流输电系统的广泛应用，电力电子设备大规模接入电网，新型电力系统的结构和运行特性发生显著变化。相对于传统同步发电机组，风电机组通过电力电子变换器并网，具有低惯性和非同步特点，在常规的最大功率点跟踪（MPPT）模式下不能对电网的频率变化做出响应，大规模并网后会引发系统惯量降低和一次调频容量不足等问题。同时，风电机组的出力具有波动性和不确定性，使得电网的频率问题日益突显［1］。

深入研究风电大规模接入电力系统的频率问题，构建能够表征实际风电机组频率响应特性的仿真模型，并准确辨识其频率控制结构和参数是关键。目前，风电机组的仿真建模研究多集中于对故障穿越特性的模拟［2］，频率方面的研究集中于调频控制策略的设计和简化频率响应模型的推导。文献［3］提出了虚拟惯量与下垂控制协同的调频策略，采用时变参数避免转子失速；文献［4］提出了基于粒子群优化（PSO）算法的风电机组下垂控制系数优化方法，减小了频率二次跌落深度。然而，在仅依靠转子动能的情况下，风电机组无法提供持续的有功支撑，需要通过减载控制留取备用容量［5］。针对此问题，文献［6］提出了一种减载系数变化的风电机组调频控制策略，使其备用功率能够得到充分释放，但未将常用的虚拟惯量控制纳入设计。在频率响应模型推导方面，文献［7-8］建立了采用综合惯量控制的风电机组频域模型，实现了对风电机组惯性支撑能力的量化分析；文献［9］在上述研究的基础上，建立了风电机组虚拟惯量的延时影响机理模型，明确了虚拟惯量延时对系统频率动态的作用；上述文献均未考虑减载备用控制对相关模型的影响，功率可调裕度较小。文献［10-11］提出了基于减载备用和下垂控制的风电机组调频响应模型，能够为系统级频率响应特性分析提供支撑；文献［12］则建立了计及机组的综合惯量控制和场站内风速差异的电力系统扩展的系统频率响应（SFR）模型，较好地反映了风电场对系统频率的影响，但缺少对于超速减载控制和桨距角减载控制的考量。总体来看，目前的主流调频控制策略基本为超速减载控制、桨距角控制、虚拟惯量控制和下垂控制的一种或多种的简单协同，机组的调频响应模型尚无法涵盖全工况和全调频控制策略。

针对风电机组参数辨识方面的研究多集中于机组主电路、稳态控制器和故障穿越控制器参数的辨识，频率控制器参数的辨识较少。文献［13］通过推导风电机组转子侧控制器的解耦模型，基于L-M 优化算法辨识了转子侧控制器务参数，但未考虑非稳态控制参数对辨识结果的影响。文献［14］将长短期记忆（LSTM）神经网络与改进粒子群优化（IPSO）算法相结合，实现了风电机组变流器比例-积分（PI）控制参数辨识；文献［15］基于PSO 分步寻优算法，解决了永磁风机变流器内环PI 参数和无功电流支撑系数无法同时辨识的难点；这两种方法仅考虑了部分低电压穿越工况，未涉及频率扰动。文献［16-17］分别采用改进的卡尔曼滤波法和最小二乘辨识算法，估算出风电机组和风电场的等效虚拟惯量参数，但无法直接确定风电机组的虚拟惯量系数。文献［18］基于狼群算法，在PSASP 平台实现了风电场一次调频参数的最优辨识。然而，机电暂态仿真模型结构与实际控制器结构可能存在较大差异，其参数辨识结果往往不能反映实际情况。可以看出，上述风电机组调频控制器参数的辨识均以频率控制器结构已知为前提，且存在算法复杂、实现难度高、难以适应实际工程的问题。

为了克服以上问题，以因风能利用率高、故障率低等优点被广泛使用的全功率型风电机组为例，建立能够覆盖国内主流型号综合调频控制的通用电磁暂态模型；基于机组调频响应特性与调频控制策略/参数的对应关系，提出采用机组实测频率响应特性曲线形态辨识调频控制器结构、采用机组实测频率响应特性曲线特征值辨识调频控制器参数的实用化辨识方法。通过与实际机组封装模型和现场试验的频率扰动响应特性的对比分析发现，本文建立的全功率型风电机组电磁暂态模型具有较高的模拟精度。

1 全功率型风电机组的通用调频控制模型

本文建立的全功率型风电机组通用模型结构如图1 所示。图中：vw为风速；ηdel为减载备用系数；PMPPT为MPPT 模式下的有功功率；Pdel为减载运行模式下的有功功率；Pref为有功功率参考值；ΔPref为有功功率参考值调节量；ωopt为MPPT 模式下的风机转速；ωdel为减载运行模式下的风机转速；ωr为实际 转 速；ωr，ref为 转 速 参 考 值；βref为 桨 距 角 参 考 值；Flag1、Flag2、Flag3 为标志位。全功率型风电机组通过风力机捕获风能，带动永磁同步发电机（PMSG）发电，再经过“背靠背”全功率变流器和机端变压器同步并网，其参与调频的方法主要包含综合惯量控制（即转子动能控制）、功率备用控制及两类间的协同控制等。

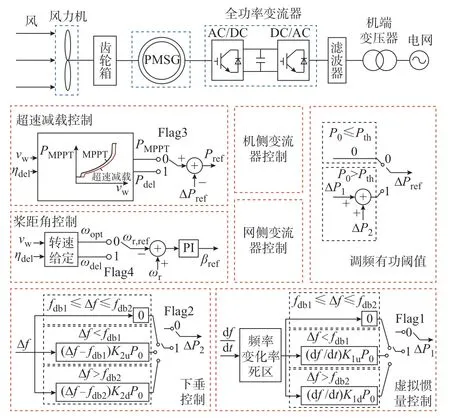
图1 全功率型风电机组的通用频率控制模型Fig.1 Generalized frequency control model of full-power wind turbines

1.1 综合惯量控制

综合惯量控制由虚拟惯量控制和下垂控制两部分构成。前者通过模拟同步发电机的转动惯量特性，利用风电机组储存的转子动能参与系统调频控制，响应系统频率的变化率，其输出特性可表示为：

式中：ΔP1为虚拟惯量控制器输出的有功调节量；P0为风电机组稳态有功输出，减载运行时P0=Pdel；K1u和K1d、fdb1和fdb2、rdb1和rdb2分 别 为 频 率 下 降 和 上升时的虚拟惯量系数、调频死区和频率变化率死区；f为系统频率；Δf为系统频率偏差；t为时间。

下垂控制在风电机组有功功率参考值的基础上，叠加了一路正比于系统频率偏差的有功功率参考值参与系统调频。响应特性可表示为：

式中：ΔP2为下垂控制器输出的有功参考值调节量；K2u和K2d分别为上、下调下垂系数。

若同时采用虚拟惯性控制和下垂控制，可使转子动能主动响应系统频率的变化率和偏差，但在转速下降至极限或频率恢复过程中，转子需吸收有功功率以提高转速，频率存在二次跌落风险。

1.2 功率备用控制

若要实现真正意义上的一次调频，风电机组须在运行时预留调频备用功率，主要有超速和桨距角减载控制两种方式。这是因为风电机组的风能利用率Cp由叶尖速比λ和桨距角β共同决定，改变λ（与转速成正比）和β可间接改变Cp，实现功率备用。

桨距角减载控制（如附录A 图A1 所示）：随着桨距角β的增大，风电机组工作点由A变为B，输出功率减小。基于此原理，桨距角控制可根据设定的ηdel实现减载运行，并在系统出现频率扰动时，实时调整桨距角调整有功输出，实现一次调频。

超速减载控制：由附录A 图A1 可以进一步看出，桨距角一定时，在每个风速下都有唯一的转速ωopt使风电机组达到最优叶尖速比λopt，从而使风电机组达到最大风能利用状态，如式（3）所示。

式中：R为风轮半径。

控制风电机组转速偏离ωopt即可实现功率减载，为调频提供功率备用。若通过降低转速实现，机组稳定性会降低，一般采用超速控制。如附录A图A1 所示，采用超速控制后，风电机组运行点由A移动至C，风能利用率由CP，max减小至CP，del，对应叶尖速比由λopt变为λdel。当系统出现频率扰动时，可通过有功功率的吸收和释放实现一次调频。

一般来讲，超速减载控制的响应速度较快，但受转速上下限的限制；变桨距角控制涉及机械部分动作，响应速度较慢且会加速机组磨损。工程上可采用二者结合的方式：低风速场景下，为保证机组功率输出的稳定性，通常不参与系统调频，可设置有功阈值Pth限制调频控制系统动作；中风速场景下，采用超速减载控制；转速受限的高风速场景下，采用桨距角控制。虚拟惯量和下垂控制贯穿中高风速场景，所生成的有功指令作用至备用控制生成的稳态减载运行功率Pdel，作为频率扰动下的功率指令值，不同调频控制策略的启用与协同可通过图1 中的标志位实现灵活选择。根据数十个风电场的实测结果分析可知，如图1 所示的全功率型风电机组的通用频率控制模型基本能够涵盖国内目前主流型号风电机组的调频策略。

2 调频控制器结构的实用化辨识

2.1 调频控制器结构与频率响应特性的对应关系

风电机组的调频响应特性由初始运行状态、稳态控制器结构和参数、频率控制器结构和参数共同决定。其中，初始运行状态和稳态控制器的辨识已有较多研究［13］，本文主要聚焦于调频控制器结构和参数的辨识。

调频控制器的结构决定频率响应的曲线形态，参数决定频率响应的幅值。辨识其控制器结构，即通过风电机组频率响应的曲线形态辨识图1 所示机组通用频率控制器结构中标志位的导通方式。不同的控制器结构（标志位导通方式）对应的典型频率响应曲线形态如图2 所示，频率设定值和频率变化率均为49.89 Hz 和0.5 Hz/s，稳态有功功率分别为0.3、0.3、0.3、0.3、0.33、0.3、0.56、0.5 p.u.。在限幅环节、死区、机组控制策略和参数等因素的共同作用下，不同工况风电机组的频率响应曲线形态并不一致。在多种多样的响应曲线形态中，图2 总结遴选出了可用于控制器结构高效辨识的8 种典型响应形态，其与调频控制器结构的对应关系具体如下。

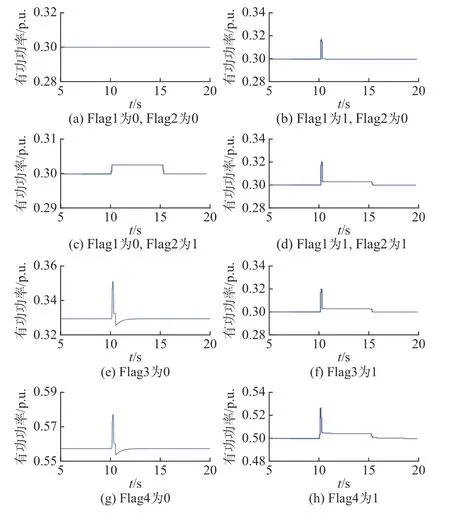
图2 典型频率响应库Fig.2 Typical frequency response library

由图2（a）至（d）可以看出，虚拟惯量控制与下垂控制对应的标志位Flag1 和Flag2 可通过风电机组在频率斜率跌落和稳定区间内的响应情况确定。若二者均为0，则风电机组不响应频率变化，有功功率始终保持不变；若Flag1 为1 且Flag2 为0，则风电机组仅在频率下降阶段增发有功功率，频率稳定和恢复阶段均无响应；若Flag1 为0 且Flag2 为1，则风电机组有功功率的上调量与频率偏差量始终呈现近似正比关系，直至调频控制强制退出或频率恢复至死区内；若Flag1 为1 且Flag2 为1，则风电机组有功功率的上调量为上述两种情况的叠加，频率跌落至稳定值时存在明显的有功跌落，但因下垂控制的存在，频率稳定期间内仍能维持有功上调。

由图2（e）至（h）可知，超速减载控制和桨距角减载控制主要影响风电机组在中风速和高风速场景下有功上调的可持续时间。由于虚拟惯量控制仅在频率跌落阶段短暂响应，一般仅依靠转子动能即可实现，故只有在风电机组配备了下垂控制的情况下，才需要减载备用控制提供持续的有功上调能力。据此，分析减载备用控制时，默认风电机组至少配备了下垂控制。在中风速场景下若Flag3 为0，则风电机组依靠转子动能仅可维持数秒的有功上调，直至调频控制因转速下限的限制而退出，有功功率出现明显跌落；若Flag3 为1，则风电机组可持续增发有功功率直至频率恢复。类似地，桨距角减载控制的标志位Flag4 也可通过风电机组在高风速场景下的有功上调可持续时间判断。

综上，本节明确了调频控制器结构与频率响应曲线形态之间的对应关系，结合充足的风电机组频率扰动实测数据即可实现调频控制器结构辨识。

2.2 调频控制器结构的实用化辨识方法

根据2.1 节不同标志位的组合方式与调频响应曲线形态的对应关系，提出调频控制器结构的实用化辨识方法，辨识次序和步骤如下。

步骤1：频率响应特性库构建。在不同风速和不同频率扰动下，对实际机组或黑盒模型进行测试，建立包含频率和有功功率数据的频率响应特性曲线库。文中，风速场景以0.5 m/s 间隔取值，覆盖切入至切出风速整个运行区间。频率扰动基于文献［19］规定的惯量响应和调频响应测试工况扩展得到，建议 频 率 变 化 率 范 围 为±0.1 ～±1 Hz/s，间 隔0.05 Hz/s；频率扰动设定值为48.0 ～51.5 Hz，间隔0.1 Hz，死区附近间隔0.01 Hz。

步骤2：频率响应特性曲线分段。将曲线库中所有实测曲线分割为扰动前稳态（t0至t1）、扰动发生时的暂态（t1至t2）、扰动稳定时的暂稳态（t2至t3）、扰动恢复时的暂态（t3至t4）和扰动后稳态（t4至t5）5 个区间。其中，t0、t1、t2、t3、t4、t5分别为测试开始时刻、扰动开始时刻、有功功率达到暂稳态的时刻、频率开始恢复时刻、有功功率达到稳态的时刻和测试结束时刻。

步骤3：调频控制器结构辨识。根据图2 可知，Flag1 的辨识对应t1至t2区间，Flag2 对应t1至t4区间，Flag3 和Flag4 对应中风速和高风速场景下的t1至t3区间。进而，按照图2 所示曲线形态与频率控制器结构的对应关系，计算待辨识曲线与图2 典型曲线的欧氏距离，获得相似性最高的曲线形态，对应选出标志位的导通方式，从而辨识出控制器结构。

至此，形成了基于频率响应曲线形态辨识调频控制器结构的方法，在此基础上即可进行调频控制器参数的辨识。

3 调频控制器参数的实用化辨识

3.1 调频控制器参数与频率响应特性的对应关系

根据图1 可知，调频控制器的关键参数包含：参与调频的有功阈值Pth、上/下调频率变化率死区rdb1与rdb2、上/下调调频死区fdb1与fdb2、上/下调虚拟惯量系数K1u与K1d、上/下调下垂系数K2u与K2d、减载备用系数ηdel和有功调节上/下限幅ΔPmax与ΔPmin。为保证风电机组运行的经济性，ΔPmax在数值上一般等于减载备用系数ηdel，无须分别辨识。此外，虽然频率跌落和上升工况下以上参数的数值可能不同，但其对频率响应特性的影响类似，本节将以频率跌落工况为例，进行调频控制参数与响应特性的对应关系分析，测试结果如图3 所示。

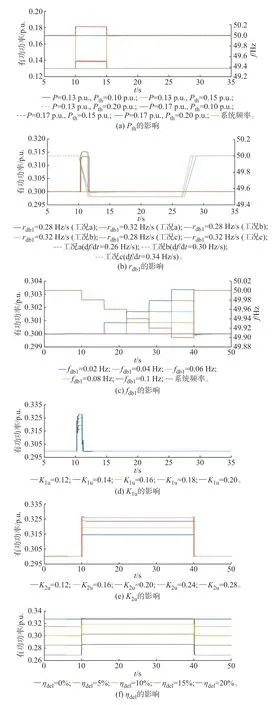
图3 不同参数对风电机组调频响应的影响Fig.3 Influence of different parameters on frequency regulation response of wind turbines

1）参与调频的有功阈值Pth

文献［19］规定风电有功功率大于0.2 p.u.时应参与系统调频。风电机组转速（功率）较低时，参与调频可能引起失速，一般不参与调频，故Pth一般大于等于0.2 p.u.。由图3（a）所示的频率扰动工况测试的结果可知，Pth的数值大小主要影响风电机组响应频率变化的稳态有功范围，Pth越大该范围越小，其中，P表示风电机组稳态运行时的有功功率。

2）频率变化率死区rdb1和调频死区fdb1

rdb1主要影响虚拟惯量控制响应频率变化率的灵敏程度，而fdb1影响综合惯量控制整体响应频率偏差的灵敏程度。图3（b）基于文献［19］给出的3 种惯量响应测试工况进行对比，频率设定值为49.5 Hz。图中：实线表示有功功率；虚线表示频率。图3（b）和（c）所示的频率扰动工况测试结果表明，两种死区的增大会增加机组的响应延迟、缩小响应频率变化的范围，但过小又将导致机组调频控制器频繁动作、增加机械损耗和频率振荡风险。文献［20］规定风电机组的一次调频死区在±0.03～0.10 Hz 范围内，文献［19］推荐的变化率死区为±0.3 Hz/s。

3）虚拟惯量系数K1u

K1u主要影响电力系统的最大频率变化率和频率最低点。测试工况同图3（b）中的工况c，测试结果如图3（d）所示，K1u的增加将提高频率变化时风电机组的有功调节量。根据文献［21］可知，风电机组的等效惯性时间常数TJ一般设置为8～12 s，换算成虚拟惯量控制系数为0.16～0.24。

4）下垂系数K2u

K2u主要影响电力系统在频率扰动期间的整体频率偏差量。测试工况同图3（a），测试结果如图3（e）所示，下垂系数的增加将提高频率扰动全程的有功调节量。根据文献［21］可知，风电机组的下垂系数一般设置在10～50 范围内。

5）减载备用系数ηdel

ηdel同时影响风电机组的稳态运行有功出力与频率扰动下的有功调节量。测试工况同图3（a），测试结果见图3（f），更大的ηdel意味着更大的有功上调空间（即ΔPmax增大），但同时降低了稳态有功出力，不利于机组的经济运行。文献［19］要求风电机组的有功调节上/下限ΔPmax与ΔPmin分别在6%～10%和10%～20%的范围内，故减载备用系数应大于6%。

由于相关标准已给出了参数范围或推荐值，辨识过程可在此基础上，根据调频控制器中务关键参数对频率响应特性的影响及灵敏度，基于建立的风电机组频率响应特性库中曲线的特征值，用简单的最小二乘算法实现实用化辨识。

3.2 调频控制器参数的实用化辨识方法

基于上述分析，待辨识参数与频率响应特性曲线特征值的对应关系如表1 所示。

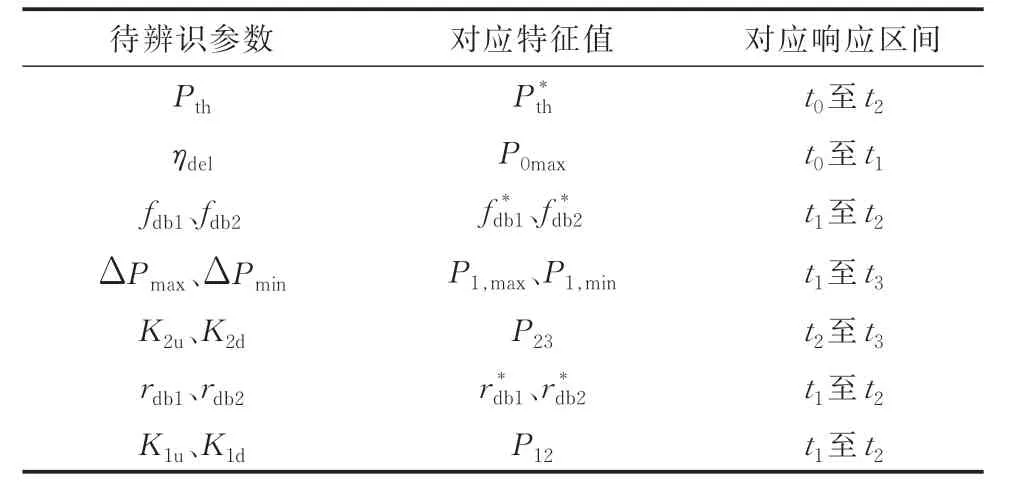
表1 待辨识参数及对应的响应曲线特征值Table 1 Parameters to be identified and corresponding eigenvalues of response curves

基于表1，本文所提调频控制器参数的实用化辨识方法的辨识次序和步骤如下。

1）步骤1：辨识参与调频的有功阈值Pth

在2.2 节建立的频率响应特性曲线库中，提取频 率 斜 率 变 化（0.1 Hz ＜|Δf|≤1.5 Hz，0.3 Hz/s ＜|df/dt|，推荐频率设定值为49、51 Hz，频率变化率为±1 Hz/s）工况下，风电机组不响应频率变化的最大稳态有功功率P即为机组参与调频的有功阈值Pth，可直接观测获得。

2）步骤2：辨识减载备用系数ηdel

提取恒功率区对应风速区间内风电机组在稳态运行期间的有功输出，即减载备用后的最大输出P0，max，由式（4）计算出ηdel为：

式中：Pn为风电机组的额定有功功率。

3）步骤3：辨识调频死区fdb1与fdb2

提取风电机组在Pth＜P0≤Psp（Psp为风电机组超速减载ηdel后恰好达到转速上限时的有功功率）对应风速范围内，频率斜率变化（0.3 Hz/s ＜|df/dt|，推荐±1 Hz/s）工况下，有功功率响应频率变化的最高频率（频率跌落工况）和最低频率（频率上升工况），即为和。fdb1与fdb2可由式（5）计算：

式中：fn为系统额定频率。

4）步骤4：辨识有功调节上/下限ΔPmax与ΔPmin

提取风电机组频率斜率变化（0.3 Hz ＜|df/dt|，推荐频率设定值为48.0 Hz、51.5 Hz，频率变化率为±1 Hz/s）工况下，频率扰动期间风电机组的最大、最 小 有 功 功 率P1，max和P1，min。ΔPmax与ΔPmin可 表示为：

5）步骤5：辨识下垂系数K2u与K2d

提取风电机组在频率阶跃变化（推荐频率设定值 范 围为48.0 Hz 至fn+fdb1和fn+fdb2至51.5 Hz），且ΔP1+ΔP2未达到有功调节上下限的工况中，t2至t3区间内的风电机组有功功率平均值，即特征值P23。然后，由式（7）计算得到下垂控制器输出的有功参考值调节量ΔP2，结合式（2）利用最小二乘法计算得到K2u与K2d。

6）步骤6：辨识频率变化率死区rdb1与rdb2

提取风电机组在频率斜率变化时（0.1 Hz ＜|Δf|≤1.5 Hz，推荐频率设定值为49、51 Hz），虚拟惯量控制模块响应频率变化的最大频率变化率（频率跌落工况）r和最小频率变化率（频率上升工况），即为频率变化率死区rdb1与rdb2。此类测试工况下，风电机组的有功调节量为虚拟惯量控制与下垂控制指令的叠加，故虚拟惯量控制的指令值为：

其中，ΔP2可由步骤3 和步骤5 的辨识结果结合扰动期间的频率数据和式（2）计算得到。

7）步骤7：辨识虚拟惯量系数K1u与K1d

提取风电机组在频率斜率变化（推荐频率设定值 范 围 为48 Hz 至fn+fdb1和fn+fdb2至51.5 Hz，频 率变 化 率 范 围 为-1 Hz/s ≤df/dt＜rdb1和rdb2＜df/dt≤1 Hz/s）且ΔP1+ΔP2未达到有功调节上下限的工况中，t1至t2区间内的有功功率平均值即为特征值P12。然后，结合式（1）、式（8）利用最小二乘法计算得到K1u与K1d。

综上，务步骤的辨识方法见附录A 表A1。从表A1 可以看出，所提全功率型风电机组调频控制器参数辨识方法不涉及复杂计算，具有较好的工程实用性。

4 方法验证

4.1 基于“黑盒”封装模型的方法验证

为验证论文所提全功率型风电机组调频控制器结构和参数的实用化辨识方法的有效性，本节以某厂家提供的MATLAB/Simulink 某型号全功率型风电机组“黑盒”封装模型为基准，参照文献［2］，对其稳态控制器进行辨识后（网侧变流器内、外环PI 参数分别为0.25、8 和10、3 500，机侧变流器内、外环PI 参数分别为0.5、17 和0.001 8、0.1），构建了通用频率控制白盒模型，如附录A 图A2 所示。根据文献［19］，对厂家封装模型在小风、大风场景（减载后有功出力分别为0.3、0.9 p.u.）下的22 种频率扰动工况进行了测试，具体见附录A 表A2 和表A3。采用提出的辨识方法，辨识出的调频控制器结构和参数见表A4。

为直观展示本文提出方法的有效性，基于附录A 表A4 的辨识结果构建的白盒仿真模型与厂家封装模型在其中6 种工况下的响应特性对比如图4 所示，有功功率在频率扰动期间的平均绝对偏差如附录A 图A3 所 示。图A3（a）的A1～A4 号 和A5～A8 号工况分别对应小风和大风场景下附录A 表A2的4 种 扰 动 工 况，图A3（b）的B1～B7 号 和B8～B14 号工况分别对应小风和大风场景下表A3 的7 种扰动工况。

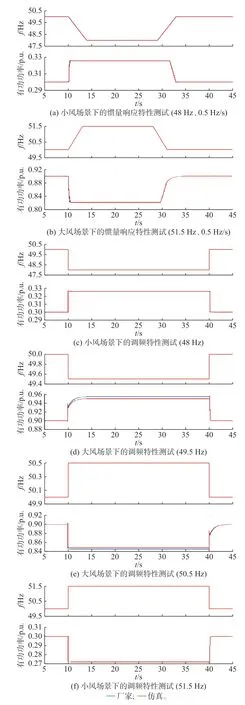
图4 “黑盒”模型与仿真模型结果对比Fig.4 Comparison of “black-box” model and simulation model results

综合图4 和附录A 图A3 可知，基于本文提出的风电机组调频控制器结构和参数的辨识方法所建立的仿真模型，在务个频率扰动工况下均能准确跟踪厂家“黑盒”封装模型的频率和功率响应特性，有功功率的平均绝对偏差小于0.005 p.u.，证明了提出方法的有效性。

为进一步验证本文方法对功率扰动引起的频率变化工况的适应性，建立了附录A 图A4 所示的由同步机、负荷和风电场组成的仿真系统，主要参数如表A5 所示。其中，风电场分别采用厂家“黑盒”封装模型和所辨识出的“白盒”模型的单机倍乘模型，风电场在负荷突增和突减工况下的有功功率和系统频率响应情况对比如图5 所示。可以看出，提出的方法仍然可以很好地模拟风电场在系统中的响应特性，对功率扰动引起的频率变化工况适应性较好，进一步证明了所提方法的有效性。

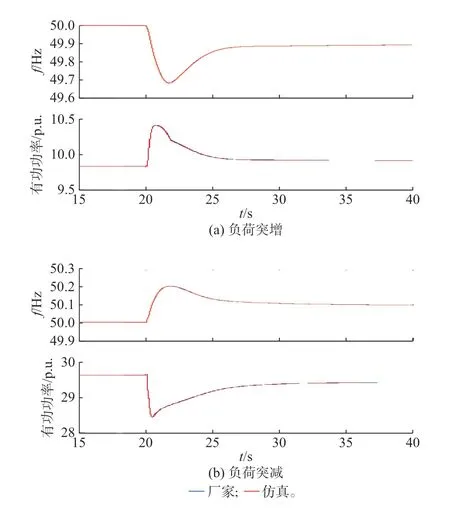
图5 负荷功率扰动下的仿真结果Fig.5 Simulation results under load power disturbance

4.2 基于现场实测的方法验证

为进一步验证本文提出的全功率型风电机组调频控制器实用化辨识方法的正确性，依据区域电网的新能源场站快速频率响应功能入网试验方案对中国某实际风电场的频率响应进行测试和辨识。根据要求，该风电场共测试了4 种工况，分别是出力为0.2～0.3 p.u.时限功率和不限功率的工况C1、C2 以及出力为0.5～0.9 p.u.时限功率和不限功率的工况C3、C4，限功率工况的所限功率不小于额定有功功率的15%。涉及的试验内容如附录A 表A6 所示。在合适的风速下重复进行试验以尽量避免实测工况的不确定性影响，每类试验内容取2 次有效试验，共20 组试验结果，采样精度为0.01 s。本文节选了工况C1 下频率阶跃跌落至49.8 Hz 的第1 次试验结果和工况C1 下频率阶跃上升至50.2 Hz 的第1 次试验结果，见图A5。

由附录A 图A5 可以看出，现场量测存在少量噪声，由于提出的调频控制器的实用化辨识方法主要关注风电机组有功响应的曲线形态和稳态、暂稳态值，现场量测噪声对辨识过程的影响较小，采用基于SUREShrink 阈值的小波去噪法，即可基本避免噪声对辨识过程的影响［22］。由于目前该地区电网调度要求实际运行的风电场机组级不实施减载备用，且制定的测试规程暂未要求参照附录A 表A2中的惯量响应特性测试工况，故该机组（整个场站的聚合等值风电机组）可辨识的参数仅包含：调频死区、有功调节上下限和下垂系数3 类。基于式（2）、式（5）、式（6）和式（7），参数辨识结果如表A7 所示，据此构建出风电机组调频仿真模型，节选图A5 对应工况的仿真模型的频率扰动响应特性进行展示，如图A6 所示。

综合附录A 图A5 和图A6 可以看出，建立的风电机组仿真模型可精确跟踪实际机组测试出的频率和功率响应特性，证明了提出的全功率型风电机组调频控制器的实用化辨识方法应用于现场试验的有效性。

5 结语

本文建立了全功率型风电机组通用频率控制模型，根据调频响应曲线的形态和幅值，明确了其与务类控制结构和参数的对应关系，提出了全功率型风电机组调频控制器结构和参数的实用化辨识方法。通过基于辨识结果构建的“白盒”模型与厂家“黑盒”封装模型及实际风电场在标准测试工况和功率扰动工况下的响应特性对比，验证了提出的实用化辨识方法应用于厂家“黑盒”封装模型和现场试验的有效性。该方法可服务于风机制造商、电网调度和研究部门，用于实际风电系统的参数校核、性能验证及控制策略设计等。

本文提出辨识方法的主要研究对象为跟网型控制的全功率型风电机组，后续将进一步验证该方法对其他类别和组网方式新能源机组的适应性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。