往复直插式麦冬播种装置的设计与优化

2024-04-28何云飞钟良党兴

西南科技大学学报 2024年1期

何云飞　钟良　党兴

摘要：為了改善川麦冬播种条件，提高播种效率，基于麦冬苗特性和农艺要求，设计了一种基于曲柄摇块机构的往复直插式麦冬播种装置，实现了以单个电机作为唯一动力完成从苗盘中取苗和播种的动作。运用Matlab编写了播种装置的运动学辅助分析软件讨论部分机构参数对运动轨迹的影响并得到了较优初始值，以理想的播种运动轨迹作为目标对参数进行优化得到了最优结果。运用Solidworks和 Adams 进行建模仿真，验证了优化结果的可行性。该研究可为麦冬播种机的设计提供理论参考。

关键词：播种装置曲柄摇块机构运动学仿真麦冬

中图分类号：S223.9 文献标志码：A 文章编号：1671-8755（2024）01-0075-10

Design and Optimization of Seeding Device for Reciprocating Linear Planting of Ophiopogon japonicus

HE Yunfei ， ZHONG Liang ， DANG Xing

（School ofManufacturing Science and Engineering ， Southwest University ofScienceand Technology ， Mianyang 621010 ， Sichuan ， China ）

Abstract： Based on the characteristics of Ophiopogon japonicus seedlings and agronomic requirements ， a reciprocating linear planting Ophiopogon japonicus seeding device based on the crank rocker mechanism was designed to improve the sowing conditions of Ophiopogon japonicus and the sowing efficiency ， which realized the use of a single motor as the only power to complete the action of picking and planting seedlings from the seedling tray. The kinematics auxiliary analysis software of the seeding device was written by Matlab to discuss the influence of some mechanism design parameters on the motion trajectory ， and the better initial value was obtained . Taking the ideal seeding motion trajectory as the target to optimize the parameters ， the optimal result was obtained . Modeling and simulating by using Solidwork s and Adams verifies the feasibility of the optimization results . This research can provide theoretical reference for the design of Ophiopogon japonicus seeder.

Keywords ： Seeding device; Crank rocker mechanism; Kinematics simulation; Ophiopogon japonicus

麦冬为百合科沿阶草属多年生常绿草本植物，具有极高的药用与保健价值。四川省三台县作为优质麦冬主要产区，麦冬产量占全国总产量的70%以上，出口产量占全国80% ，是中国国家地理标志产品[1-3]。由于川麦冬的播种环节完全依靠人工，生产效率低，劳动强度大，阻碍了川麦冬种植业的发展。实施农业机械化可以减少劳动力的投入，提高农业生产效率，是现阶段在农作物种植上降低人工成本、提高农业经济效益的有效手段[4]。欧美等发达国家从20世纪20年代就开始了播种机械化研究，由于地广人稀，人均耕地面积较大，设计的自动播种装置多以大型、高速为主，播种效率高、工作稳定，适用于大田大规模种植，现已实现播种机械化[5-8]。我国播种栽植机械研究起步较晚，20世纪70年代才开始研发。由于我国种植农作物的种类繁多，目前小麦、水稻、玉米等大田农作物播种栽植的机械化程度较高，而瓜果蔬菜、花卉苗木、中药材等作物的播种栽植机械化在经济性、实用性方面不尽人意[9-10]。

现已成熟的播种栽植装置主要有钳夹式、导苗管式、链夹式、扰性圆盘式和吊篮式。近年来，针对特定作物的播种装置相继出现。黄磊[11]设计了一种两行乘坐式蔬菜穴盘苗自动栽植机。采用整排间隔取苗，具有穴苗自动输送、分苗机构依次投苗和鸭嘴栽植器同步栽植等功能。张凌峰[12]测试了芦蒿苗杆形态、弯曲强度等物理性质，分析了芦蒿苗杆在载荷施加下的位移变形，通过改进栽植机的鸭嘴式机械结构来实现芦蒿的扦插动作。姚晗[13]设计了一种挠盘式大葱栽植机，研究了挠盘式播种装置的特征参数和葱苗在挠盘中的运动轨迹，对葱苗运动参数和挠盘聚合角进行了计算分析。上述研究都是通过改进已成熟的播种栽植装置来满足不同作物的种植需求，但对于种植要求特殊的中药材等作物不具有适用性，所以运用现代设计方法，针对有较高价值的农作物的形貌特征和播种要求设计播种栽植装置成为热点[14]。

为了减轻麦冬种植户的劳动强度，提高种植效率，降低经济成本，本文针对川麦冬苗的形貌特征以及种植的农艺要求，设计了一种基于曲柄摇块机构的往复直插式麦冬播种装置，利用曲柄摇块机构的特点，实现了以单个电机作为唯一动力完成从苗盘中取苗和播种的动作。建立了播种装置的运动学数学模型，利用Matlab编写了麦冬播种装置的运动学分析软件，分析讨论了部分参数对播种轨迹的影响，以理想的运动轨迹为目标对机构参数进行了优化设计，利用Solidwork s 和 Adams 建立播种装置的虚拟样机验证了优化结果的可行性。

1 麦冬播种装置设计要求

麦冬苗根状茎短粗，生多数须根，直径0.10～0 .25 cm ，长12～40 cm ，宽0.3～0.7 cm ，光滑，具脉5～13条。播种方式为分株播种，每年4月将母株挖出后去掉块根，选择较为优质的苗切须做种，其种植深度为3～5 cm ，株距为7～9 cm ，行距为7～12 cm。现有的播种机不能满足川麦冬的播种要求[15-16]。

根据川麦冬种植的农艺以及种植户的要求，麦冬播种装置的设计应满足以下要求[17]：结构简单，操作方便；栽种直立度高，保证麦冬苗正常生长；制造成本低，农户易接受。

2 麦冬播种装置工作原理

2.1 麦冬播种装置设计

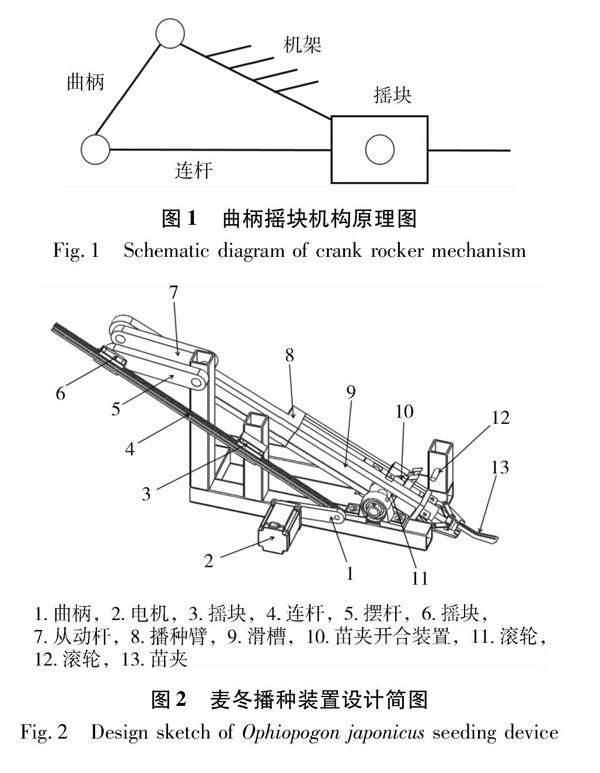
如图1所示，曲柄摇块机构以曲柄作为主动件，曲柄做旋转运动，通过连杆驱动摇块做往复摆动，其特点是在单一的动力条件下连杆与摇块可以做转动和滑动的复合运动[18]。利用这一特点，以曲柄摇块机构结构为主，设计了一种往复直插式麦冬播种装置实现取苗和播种，并采用排插式保证行距。

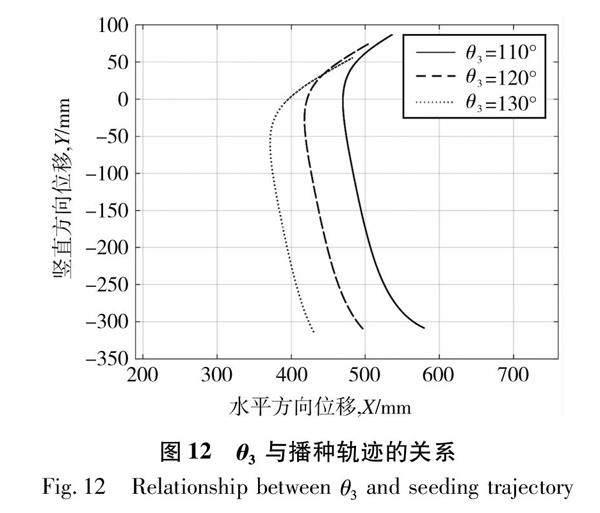
图2为一个工位的麦冬播种装置的简图。该麦冬播种装置由摆角放大机构和播种机构组成。摆角放大机构由驱动电机、摇块、连杆、摆杆组成，作为播种装置的动力输入部分。播种机构主要由从动杆、播种臂、苗夹、滚轮、挡杆组成，滚轮可在播种臂侧板的槽中转动，播种臂末端装有苗夹，苗夹开合装置通过与挡杆配合可控制苗夹开合。

2.2 工作原理

图3为摆角放大机构的原理图，其中 AB 为输入曲柄，AE 为机架，与竖直方向有一个倾斜角度，曲柄 AB 与连杆 BH 组成转动副，连杆 BH 与摇块1、摇块2组成移动副，摆杆 ED 与摇块2组成转动副。曲柄回转时，连杆 BH 既以摇块1的中心 C 点转动又与摇块2作相对滑动，从而使 ED 绕点 E 处轴实现大角度摆动。

图4为播种机构的原理图，滚轮与播种臂侧板滑槽的相对运动可简化为曲柄摇块机构。从动杆 EF 作为输入曲柄，摆杆 ED 始终与从动杆 EF 平行。 EG 为机架，FQ 为播种臂，曲柄 EF 与播种臂 FQ 组成转动副，播种臂 FQ 与摇块3组成移动副，摇块3 与机架 EG 组成转动副。当 EF 进行圆周运动时，播种臂 FQ 末端苗夹 Q 点的运动轨迹为一对称的蚌型曲线，对称轴与 Q 点、E 点连线重合，蚌型曲线的顶点在该对称轴上。当从动杆 EF 跟随摆杆 ED 在一定范围内摆动时，Q 点的运动轨迹是蚌型曲线的一部分，成“7”字形。

根据总体设计，进行播种动作时整机不移动，所以整机每移动一个株距停止后，曲柄 AB 旋转一周，带动播种臂 FQ 运动，通过播种臂上的苗夹开合装置控制苗夹在 Q1 点抓取麦冬苗，苗夹处于 Q3 点松开幼苗并且速度为零，完成播种动作，即 Q1 Q2为取苗段，Q2 Q3 为播种段，Q3 Q1为返程段。

曲柄摇块机构拥有急回特性，返程比往程要快，为了保证麦冬苗栽插平稳，通过电机驱动曲柄 AB 顺时针旋转，使取苗播种的速度小于返程的速度。

3 麦冬播种装置分析模型的建立、参数的优化及验证

3.1 运动学模型的建立与参数影响分析

3.1.1 运动学模型的建立

由于传统图解法的计算效率以及计算精度并不理想，所以采用复数矢量法代替图解法，对往复直插式麦冬播种装置进行动力学分析，通过机构之间的位置关系建立方程，并对时间进行求导，得到各构件的位移、速度、加速度方程[19]。

根据复数矢量法的相关原理，以曲柄 AB 输入轴 A 点位置为中心建立坐标轴，将麦冬播种装置分为多个封闭的矢量图形，分别建立矢量方程。如图5所示，该装置能够分成3个不同的封闭矢量图形。

（1）封闭的矢量图型 ABC

将lAB ， lBC ， lAC设为矢量，得到矢量方程：

其复数形式表示为：

将式（2）分离实部与虚部，得：

由式（3）可求得变量：θ2， lBC。

式（3）对时间 t 求一次导数，得到速度关系式：

由式（4）可得变量：ω2 ， l BC 。

式（3）对时间 t 求二次导数，得到加速度关系式：

由式（5）可求得变量：a2 ， l BC 。

式（1）-式（5）中：ω1为lAB转动的角速度；ω2为lBC转动的角速度；a1 为lAB转动的角加速度；a2为lBC转动的角加速度；l（·）BC 为lBC变化的速度；l（··）BC 为lBC变化的加速度。

（2）封闭的矢量图型 CDE

将lCE ， lED ， lCD设为矢量，得到矢量方程：

lCE + lED = lCD

其复数形式表示为：

lCE e iθ4+ lED e iθ6= lCD e iθ5

将式（7）分离实部与虚部，得：

lCE cosθ4+ lED cosθ6= lCD cosθ5

由式（8）可求得變量：θ6， lCD。

式（8）对时间 t 求一次导数，得到速度关系式：

由式（9）可求得变量：ω6 ， l CD 。

式（8）对时间 t 求二次导数，得到加速度关系式：

式（6）-式（10）中：ω5 为lCE转动的角速度；ω6为lDE转动的角速度；a5为lCD转动的角加速度；a6为lCD转动的角加速度；l（·）CD 为lCD变化的速度；l（··）CD 为lCD变化的加速度。

（3）封闭的矢量图型 EFG

将lEF ， lEG ， lFG设为矢量，得到矢量方程：

其复数形式表示为：

将式（12）分离实部与虚部，得：

式（13）对时间 t 求一次导数，得到速度关系式：

由式（14）可得变量：ω8 ， l FG 。

式（13）对时间 t 求二次导，得到加速度关系式：

由式（15）可求得变量：a8 ， l FG 。

式（11）-式（15）中，ω7为lEF转动的角速度；ω8为lFG转动的角速度；a7为lEF转动的角加速度；a8 为lFG转动的角加速度；l（·）FG 为lFG的变化速度；l（··）FG 为lFG的变化加速度。

对播种臂末端苗夹 Q 点的运动状态进行分析。

Q 的坐标位置方程为：

Q 点的速度方程：

Q 点的加速度方程：

Q 点运动方程的变量可根据几何关系由上述封闭矢量图形運动方程的变量传递得到。由图5可知，θ3=θ4， θ2=θ5， θ6=θ7。

3.1.2 机构的压力角分析

为了保证传力性能良好，机构压力角一般不超过40°，当压力角接近90°时，机构会产生自锁，从而不能运转。

如图6所示，杆 BH 对杆 EF 的作用力 FD 与 D 点的速度 VD 之间的夹角“为该机构的压力角，由

图6可推导出计算公式为：

现已确定设计参数lAB =141 mm ， lAC =181 mm ， l CE =146 mm ， lED =180 mm 。根据上节已推出的公式，以曲柄 AB 朝 X 轴正方向为初始位置，得到曲柄顺时针旋转一周压力角的变化如图7所示。当摆杆 ED 与机架 EC 重合时，压力角达到最小，当摆杆 ED 到达极限位置时，压力角达到最大，压力角在机器运动过程中始终不超过40°，所以传力效果满足设计要求。

3.1.3 部分机构参数与播种轨迹的关系

根据第二节方程建立麦冬播种装置运动的数学模型，利用Matlab 2020b 中的 GUI 模块编写辅助分析软件，其人机交互界面如图8所示，通过输入麦冬播种装置不同的参数可得到不同的播种轨迹以及运动学特性，通过分析可总结出各变量对轨迹的影响规律，并以理想作业性能为目标进行参数优化。

现已确定曲柄 AB 长度lAB、机架 AC 长度lAC、机架 CE 长度lCE、摆杆 ED 长度lED ，讨论曲柄 EF 长度lEF、播种臂 FQ 长度lFQ、机架 EG 长度lEG、机架 AE 的安装倾角θ3、机架 EG 与水平方向上的夹角θ9对运动轨迹的影响。

曲柄 EF 长度lEF与播种轨迹的关系如图9所示。lEG =400 mm ， lFQ =800 mm ， θ9= -25°， θ3=120°。随着lEF增大，播种轨迹蚌型曲线对称轴的位置不变，轨迹的空间位置沿着对称轴左移；取苗段与水平线之间的夹角不变，入土角度不变。

播种臂 FQ 长度lFQ与播种轨迹的关系如图10所示。lEF =200 mm ， lEG =400 mm ， θ9= -25°， θ3=120°。随着lFQ增大，播种轨迹蚌型曲线对称轴的位置不变，轨迹的空间位置沿着对称轴右移；取苗段与水平线之间的夹角增大，入土角度增大。

机架 EG 长度lEG与播种轨迹的关系如图11所示。lEF =200 mm ， lFQ =800 mm ， θ9= -25°， θ3=120°。随着lEG增大，播种轨迹蚌型曲线的顶点位置不改变、形状发生改变；取苗段与水平线之间的夹角减小，入土角度增大；取苗段行程和播种段的行程减小。

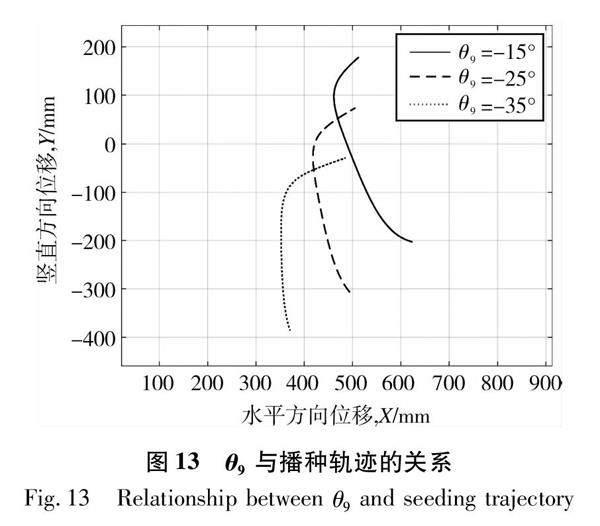
机架 AE 的安装倾角θ3与播种轨迹的关系如图12所示。lEF =200 mm ， lEG =400 mm ， lFQ =800 mm ，θ9=- 25°。根据设计，θ3增大，θ7也随之增大，播种轨迹蚌型曲线的形状不改变、对称轴位置向左下方平移，取苗段与水平线之间的夹角不变、入土角度不变，取苗段的行程增加、播种段的行程减小。

机架 EG 与水平方向上的夹角θ9和播种轨迹的关系如图13所示。lEF =200 mm ， lEG =400 mm ， lFQ =800 mm ， θ3=120°。随着θ9增大，θ9对播种轨迹的蚌型曲线形状不变，对称轴位置变化较大，取苗段的行程增加，播种段的行程减小。

3.1.4 结构参数对播种的影响分析

轨迹曲线改变会影响苗盘的安装位置和倾斜角度、麦冬苗播种的位置、入土角度、播种深度。

麦冬苗根茎较短，抓取位置有限，取苗段与水平线之间的夹角偏大，会使苗夹不容易从根部抓稳麦冬苗且苗根与苗盘之间容易发生接触，无法将麦冬苗从苗盘中顺利取出；当取苗段过短时，播种臂可能会与其他机构发生干涉；苗夹的入土轨迹为倾斜直线，在到达播种位置后，苗夹出土时需要张开，苗夹两侧插孔增大，在镇压轮到达播种位置之前，幼苗主要靠前后土壤黏附保持直立，但倾斜角度有一定限制范围，过大过小都不利于播种；蚌型曲线是对称图形，当播种段过长时，播种段末端轨迹会发生弯曲，严重影响播种麦冬苗的直立性。

根据以上分析，播种机构部分参数偏大和偏小会对播种轨迹产生影响，减小lFQ的值，增加lEG ， θ3， θ9的值能使对应的轨迹更符合要求，lEF不能确定其优化方向。

结合 GUI 界面输出的图形，人工调整参数可得到一组较优参数：lEF =200 mm ， lEG =400 mm ， lFQ =850 mm ， θ9=- 30°， θ3=130°。该组参数并非最优参数。通过建立优化模型进行优化设计，对结构参数做进一步优化[20]。

3.2 优化设计

3.2.1 基本参数

优化设计在考虑轨迹参数的同时还需要考虑机构的其他参数用于确定设计变量、优化目标和约束条件。如图14所示，可得到以下关系式：

图14中，Φ1 为苗夹处于 Q3 点时曲柄 EF 与水平方向的夹角；Φ2 为机架 EG 与水平方向的夹角；Φ3为 F3 Q3 与水平方向之间的夹角；H 为 EF 轴离地面的高度；hy为取苗点高度；h 为播种深度；L 为播种点至过 EF 所作铅垂线的距离；λ1为入土角；λ2 为取苗段与水平方向之间的夹角。

3.2.2 设计变量

确定摆角增大机构部分参数lAB =141 mm ， lAC =181 mm ， l CE = 146 mm ， lED = 180 mm ， H =550 mm ，使 EF 摆动的角度刚好达到180°，此时Φ2 =-θ9， Φ1=90°+θ3。结合上一节确定的5个参数作为变量，X =[lEF ， lEG ， lFQ ， Φ2 ， θ3]。

3.2.3 目标函数

根据上一节的分析，为了保证顺利取苗，取苗段与水平线之间的夹角λ2尽可能小，由此确定的目标函数为：

3.2.4 约束条件

（1）曲柄摇块机构中，曲柄与机架共线时，曲柄与机架长度之和必须大于连杆的长度，否则连杆会从摇块中脱离，所以曲柄摇块机构机架 EG 与曲柄 EF 长度之和不能超过播种臂 FQ 的长度，即：

（2）为了避免播种段末端轨迹发生较大弯曲，影响播种麦冬苗的直立性，曲柄与连杆的夹角不能超过90°，即：

（3）川麦冬苗栽种过深会被泥土压倒，栽种过浅容易倒伏，导致减产。根据川麦冬苗种植要求，栽种深度应在30 mm 到50 mm 之间，即：

（4）为了保证麦冬苗的直立度，入土角的范围应在65°到75°之间，即：

（5）各构件尺寸具有一定的限制，故各自变量的上下界的约束条件为：

3.2.5 优化结果与分析

该问题是有约束非线性規划问题，可采用障碍函数内点法进行求解。内点法的基本思想是：通过引入效用函数的方法将约束优化问题转换成无约束问题，再利用优化迭代过程不断地更新效用函数，使得算法收敛。使用内点法对目标函数进行优化计算的过程中，其迭代过程是在可行域中进行的，所以初始点的选择必须在可行域范围之内，通过构造增广函数，对可行域的边界设置罚函数，当迭代过程中的值接近可行域边界时，目标函数值增大，使迭代点返回可行域内部继续寻找最优点[21]。

对约束条件进行变形并取对数构造障碍函数：

式中 r 为障碍因子。

内点法迭代步骤为：首先给定初始值、允许误差、缩小系数和初始障碍因子；其次在约束集合中求出一个内点；然后以该点为初始点在障碍函数中进行迭代计算；最后检测该点是否满足小于等于允许误差，如果满足就停止迭代，否则就继续迭代计算。

以人工调参得到的值为初始值。给定初始ri等于1、缩小系数等于0.1、允许误差等于0.01进行计算。优化结果如表1所示。

往复直插式水稻插秧机栽插机构的工作原理与本文的播种机构运动原理相同，根据《农业机械设计手册》[22]中提供的现有的往复直插式水稻插秧机设计参数 H =590 mm ， hy =272 mm ， h =70 mm ， L =488 mm ， lEF =180 mm ， lEG =368 mm ， lFQ =732 mm ， Φ2=39°，Φ2=9°，曲柄回转角度为188°，通过计算可得到其λ2=20.2°。根据本设计优化前人工调参得到初始解的目标函数值λ2=22.9°。优化后得到最优解的目标函数值λ2=9.9°，通过对比结果表明优化效果显著。

如图15所示，优化后的轨迹满足播种要求，可使苗盘安装倾斜角减小，苗夹更容易准确夹紧麦冬苗根部。

3.3 运动仿真

为了验证使用Matlab优化后参数的可行性和合理性，首先采用Solidwork s 以曲柄 AB 输入轴为坐标原点，根据优化后的参数建立三维实体模型，再将模型导入 Adams 进行运动学仿真，可得到麦冬播种装置的完整的动作流程和运动轨迹，可检查优化后播种装置的运动是否产生干涉现象，验证是否满足麦冬苗播种的技术要求[23]。

Adams 中的虚拟样机如图16所示。播种机苗夹处的运动轨迹与上节优化后的运动轨迹基本一致，机器能够正常运转且无干涉现象，满足播种的技术要求。选择苗夹下端点 Q 点作为检测点，测量其在空间中的运动轨迹、位移与速度。

如图17（ a ）所示，地面纵坐标 y =-295 mm ，播种点纵坐标 y =-335 mm ，取苗点纵坐标 y =-87 mm ，入土角度为71°，满足播种要求。

如图17（b）所示，曲柄 AB 顺时针旋转一周完成一次播种，设ω= rad/s ，把曲柄旋转角度作为横坐标，Q 点竖直方向上的分速度和水平方向上的分速度第一个交于0的点为播种点，第二个交于0的点为取苗点，取苗播种段的速度远小于返程速度，可保证麦冬苗的稳定播种，满足设计要求。

4 结论

（1）利用曲柄摇块机构的运动特点，设计了一种适用于川麦冬的往复直插式播种装置，分析了其工作原理，建立了播种装置的运动学模型。

（2）用Matlab GUI 模块编写了播种装置运动学辅助分析软件，分析了部分机构参数对播种轨迹的影响，为后续优化提供了初始值。

（3）以取苗段与水平线之间的夹角最小为目标，用障碍函数内点法对各参数进行优化得到了最佳参数。

（4）利用Solidwork s 建立优化后的三维模型，用 Adams 进行仿真分析，验证优化结果符合理想播种轨迹，满足设计需求。该装置可实现川麦冬机械化播种。

参考文献

[1] 帕坦姆汗·阿布杜合力克．川麦冬种植效益及影响因素研究[D].四川绵阳：西南科技大学，2021.

[2] 杨涛，凌宁，李晓晓，等．四川根茎类中药材生产全程机械化现状与展望[J].中国实验方剂学杂志，2022 ，28（9）：248-257.

[3] 吴发明，刘莎，李敏．四川麦冬产业现状与发展前景分析[J].北方园艺，2019（17）：151-157.

[4] 杨先超，马月虹．设施内蔬菜机械化育苗移栽的现状与发展趋势[J].农机化研究，2022 ， 44（7）：8-13 ， 32.

[5] RAHUL K ， RAHEMAN H ， PARADKAR V . Design and development of a 5R 2DOF parallel robot arm for handling paper pot seedlings in a vegetable transplanter [J]. C om- puters and Electronics in Agriculture ， 2019 ， 166：105014.

[6] WEN C J ， WANG H L ， WANG M ， et al. Design and simulation analysis of a transplanting mechanism for rice transplanter [ J]. Journal of Physics ： C onference Series ， 2018 ， 1087（4）：42066-42067.

[7] KUMAR U ， THOMAS E V . Determination of force acting on the rice transplanter finger [J]. Agricultural Engineer- ing International： CIGR Journal ， 2015 ， 17（1）：30-43.

[8] CHEN M H ， CHEN X J ， WANG M ， et al. Ophiopogon japonicas ： a phytochemical ， ethnomedicinal and pharma-cological review [ J ]. Journal of Ethnopharmacology ， 2016 ， 181：193-213.

[9] 曹忠亮，郭登科，王蠫，等．旱地蔬菜移栽机移栽机构设计与试验[J].农机化研究，2021 ， 43（6）：79-83.

[10]李林林，邓干然，林卫国，等．作物移栽机械栽植机构发展现状与趋势[J].现代农业装备，2022 ， 43（1）：2-7.

[11]黄磊．乘坐式全自动移栽机车架结构仿真分析与优化[D].江苏镇江：江苏大学，2016.

[12]张凌峰．芦蒿自动扦插机的设计[D].南京：南京农业大学，2019.

[13]姚晗．挠盘式大葱自动移栽机的设计与试验[ D].济南：山东农业大学，2021.

[14]雷瀚洋．麦冬栽植机結构设计与研究[D].成都：西华大学，2021.

[15]罗守萍，陈媛媛，张超，等．川麦冬栽培关键技术探讨[J].中国现代中药，2021 ， 23（9）：1649-1654.

[16]罗俊，刘宇，蒋辉霞，等．麦冬机械化收获根茎土壤分离装置的设计研究[J].南方农机，2022 ， 53（10）：1-4 ， 8.

[17]李俚，马甲辰，范业增，等．罗汉果采摘装置的设计仿真与试验[J].农机化研究，2022 ， 44（3）：65-70.

[18]刘宝华，魏民，陶颖．基于曲柄摇块机构的封盖机设计与仿真[J].包装工程，2018 ， 39（5）：158-162.

[19]马东升，刘鑫．八连杆冲压机构工作参数矢量优化方法[J].机械设计与制造，2021（9）：51-54.

[20]陈建能，周赞，贾江鸣，等．基于大蒜根盘特征的精确切根机构优化设计[ J].浙江农业学报，2021 ， 33（11）：2174-2184.