挖掘机液压混合动力系统跟踪控制研究

王金莉，朱 娟

（1.长春光华学院电气信息学院，吉林 长春 130000；2 长春工业大学机电工程学院，吉林 长春 130000）

1 引言

挖掘机因其能够承受高惯性力，使其成为能量回收的理想选择，因此带有电动存储装置的混合式挖掘机系统被引入市场[1]。在混合系统中，电动机被安装作为驱动执行器，电容器被安装用于存储制动过程中的动能，可以节省高达41%的能源。然而，上述挖掘机混合动力系统最大的缺点是成本高，且算法的控制性能不高[2-3]。因此，针对挖掘机液压混合动力系统，提高系统模型的鲁棒性和算法的控制性能是一重中之重的研究方向[4-5]。大量的学者对挖掘机混合动力系统和提高系统的控制性能做了深入的研究[6-8]。例如，文献[9]研究了挖掘机混合动力系统的二次控制问题，考虑了载荷变化等参数的不确定性，根据鲁棒裕度、灵敏度降低和跟踪性能给出的指标，构造了多输入多输出定量反馈（MIMO QFT）控制方案。仿真实验表明MIMO QFT控制器显示了良好的跟踪性能；文献[10]阐述了基于混合动力系统的液压挖掘机采用混杂能源体系驱使的研究意义及背景，提出了在液压挖掘机中混杂能源体系驱使的控制策略方法。

该控制策略采用并联型架构，并将电机以参变量搭配方式与发动机组合；文献[11]平衡了挖掘机的负载功率，建立了由液压系统、柴油机和多体动力学模型构成的挖掘机系统模型，将其和试验数据实行了对比分析，并对仿真模型进行了相应的验证；文献[12]针对挖掘机液压混合动力模型的节能问题，对辅助动力系统进行了改进，主要研究了多控制策略的参数匹配问题。建立了系统主要元件数学模型，仿真结果表明:较原系统，参数匹配后的混合动力系统节油率提高了9.8%，工作效率提升了9.72%。虽然，上述控制方法对挖掘机混合动力系统进行了一系列的控制研究和改进，但是没有考虑到参数的不确定性和系统的非线性，无法保证系统的暂态性能和最终跟踪精度。

为此，建立了挖掘机液压混合动力系统，该系统通过改变液压单元的位移来控制执行器，或者在液压单元位移固定的情况下改变发动机的转速来控制执行器。结合了反馈控制，采用改进的自适应鲁棒控制（ARC），使系统模型具有足够大的反馈增益，从而在存在干扰的情况下实现高精度的跟踪和控制稳定性。

最后对挖掘机液压混合动力系统中的斗杆、动臂和铲斗的倾角进行跟踪仿真实验，给出了系统模型回转位置和速度的跟踪误差，并与PI控制方法进行了比较分析。

2 挖掘机液压混合动力系统结构

对挖掘机液压混合动力系统进行构建，如图1所示。

图1 挖掘机液压混合动力系统原理图Fig.1 Schematic Diagram of Hydraulic Hybrid Power System of Excavator

挖掘机液压混合动力系统主要由发动机、液压单元、恒压流量源、减压阀、止回阀和执行器组成。该系统通过改变液压单元的位移来控制执行器，或者在液压单元位移固定的情况下，通过改变发动机的转速来控制执行器。为补偿执行器的压差容积，将先导式（PO）止回阀连接到恒压流量源，该压力源通常包括一个固定排量的外齿轮泵和一个用于设定压力水平（通常在（15～30）bar之间）的安全阀，并安装了一个低压蓄能器使外齿轮泵的容积排量最小化，从而减少总损失。

3 挖掘机液压混合动力系统建模

3.1 液压系统模型

液压系统模型中每个线性执行器的负载执行器动力学可以使用压力恢复方程来表示：

式中：p1—执行器内径压力；p2—执行器杆侧的压力；V1—第一个执行器腔中的流体体积；V2—第二个执行器腔中的流体体积：

式中：Vdead—假定的气缸死容积；Abore—内径区域；Arod—杆侧区域；x—执行器位移，其时间导数表示执行器速度；xmax—执行器最大位移；VL—线体积；K—有效体积模量；QLi—穿过执行器室的内部泄漏流量；Qr1、Qr2—安全阀的流量：

式中：Cr—线性流量系数；psetting—安全阀压力设定值。泵的流量Q1和Q2以及它们的体积损失Qs是根据机组的转速、排量和压差计算出来的。最后，Qck1和Qck2表示PO止回阀的流量：

式中：aD—阀门流量系数；dPO—PO止回阀阀芯直径；plp—低压系统压力。在这种情况下，该压力被假定为一个恒定值，y1—PO止回阀阀芯位移。对于Qchk1，线轴运动可以用：

式中：APO—PO止回阀芯区域；Fcrack—阀门开裂力；k—阀门弹簧常数；rPO—阀门先导比。由于PO止回阀的快速特性，因此忽略了其动力学特性，并限制了阀芯位移以防止振荡和避免空化。

3.2 挖掘机动力学模型

由式（10）～式（12）给出挖掘机各分量的惯性张量：

由于所提出的ARC控制是基于被控对象，因此建立了挖掘机混合动力系统的详细数学模型：

式中：J(Iarm，Iboom，Ibucket)—挖掘机驾驶室的惯性，它是斗杆、动臂和铲斗执行器长度Iarm，Iboom，Ibucket的函数；φ—挖掘机驾驶室的角位置，其第一和第二时间导数是驾驶室速度和加速度；VM—液压马达最大容积排量；dp—液压马达压差；iTOT—液压马达小齿轮与座舱齿圈的总传动比；βM—液压马达标准排量；b—粘性摩擦系数；Tc—库仑摩擦系数；Ti—挖掘机驾驶室在斜坡上的重量引起的扭矩函数；α—倾角。

3.3 发动机模型

发动机动力学为：

式中：JE—惯量；nE—转速；MEeff=MEth-Mf—有效扭矩输出；MEth—发动机理论扭矩输出；Mf—发动机摩擦扭矩损失；ML—由液压系统施加在发动机上的负载扭矩。

需要注意的是，最大理论发动机扭矩MEth可以从发动机节气门全开（WOT）的测量数据中获得，其中包括摩擦。因此，为了获得最大的理论发动机扭矩，必须修改WOT测量值，以消除测量到的摩擦：

式中：uE—任何运行发动机转速下的标准化发动机控制输入；MWOT—测得的WOT曲线扭矩。摩擦定义为：

有效平均压力可以表示为：

式中：Veng—发动机排量（L）；M—平均有效压力产生的扭矩。摩擦产生的扭矩损失可以表示为：

式中：Sp—活塞速度（m/s）。

考虑到发动机的活塞位移：

4 控制设计

所设计的ARC 结构图，如图2 所示。该控制方法与传统ARC控制的优势在于，它不使用平滑投影或对自适应规律进行平滑修改，而是使用不连续投影。从而使基于不连续投影的方法更容易实现，减少了由于参数不确定性而引起的模型非线性。

图2 ARC结构图Fig.2 Arc Structure Diagram

首先，假设所有不确定性都有界：

由于控制器的设计基于不连续投影映射，因此设是θ的估计值，θ为误差：

定义不连续投影：

将式（23）中的投影向量用于式（24）给出的自适应规律中：

式中：Γ—对角正适应率矩阵；τ=φ(x)e，φ(x)—回归向量。

由于挖掘机混合动力系统中，操纵杆指令将最终控制座舱速度，因此操纵杆信号被规范化并用作速度指令。最大驾驶室速度接近0.9 rad/s，控制器的目标是尽可能接近期望的驾驶室速度。为了实现这一点，基于式（13）创建了一个非线性状态空间：

为了防止数值误差，将式（27）中的状态空间使用比例因子Sc进行缩放：

对于在线自适应规律，需要基于式（28）的线性参数化状态空间：

未知的线性参数可以定义为θ1=SciTOTdpVM∕J、θ2=b∕J、θ3=Tc∕J和θ3=Ti∕J。

由于式（29）中的第一个方程不包括不确定性，因此可以直接为前两个方程构造一个ARC Lyapunov函数，以便x1尽可能接近地跟踪期望轨迹x1d（t）。

开关函数定义为：

误差动态可以通过：

式中：βM—输入转矩的分数。

因此虚拟控制规律为：

式中：ua—自适应参数，因此鲁棒控制规律为：

其中，鲁棒控制的第一部分为：

通过定义半正定Lyapunov函数来表示自适应控制律：

考虑到式（32）～式（34）中的表达式，将输入偏差定义为e3=βM-u2，则式（36）中Lyapunov函数的时间导数变为：

其中回归向量φ为：

最后，根据式（37）和式（38），ARC控制可以表示为：

通过忽略轴向柱塞马达在液压混合系统中的阀芯动力来简化ARC控制器。此外，由于ARC控制是通过强反馈来确保稳定性，因此利用式（35）中的线性稳定反馈控制规律，在指定的范围内使其具有足够大的反馈增益，从而在存在干扰的情况下实现了高精度的跟踪和性能。

ARC控制器参数的取值，如表1所示。此外，线性稳定反馈增益kr1=4.0、kr2=0.3，比例因子Sc=1e5，自适应矩阵Γ=diag｛0.5，0.3，0.1，0.3｝。

表1 ARC控制器参数取值Tab.1 Arc Controller Parameter Values

5 实验结果

根据挖掘机液压混合动力系统的建模和ARC控制设计，在Matlab ∕Simulink环境下，对挖掘机斗杆、动臂和铲斗进行跟踪仿真实验，并给出系统的位置和速度的跟踪误差以评估其的性能。其仿真实验参数，如表2所示。

表2 挖掘机液压混合动力系统模型的仿真实验参数Tab.2 Simulation Experimental Parameters of Excavator Hydraulic Hybrid System Model

挖掘机在（-90～90）°回转指令下，完全缩回铲斗执行器和完全伸出斗杆和动臂执行器时斗杆、动臂和铲斗的回转控制倾角θ的跟踪仿真结果，如图3～图5所示。

图3 斗杆倾角跟踪曲线Fig.3 Bucket Rod Inclination Tracking Curve

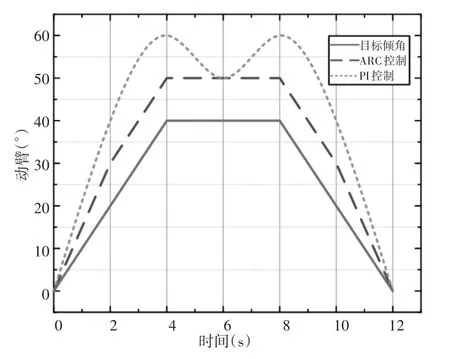
图4 动臂倾角跟踪曲线Fig.4 Tracking Curve of Tilt Angle of Boom

图5 铲斗倾角跟踪曲线Fig.5 Bucket Inclination Tracking Curve

从图中可以看出，挖掘机液压混合动力系统在没有负载的情况下，基于PI控制的斗杆、动臂和铲斗倾角的最大振幅波动率分别为50%、40%、66%，而基于ARC控制的斗杆、动臂和铲斗倾角的最大振幅波动率分别为25%、18%、35%，大幅度减小了倾角的波动范围，对挖掘机液压混合动力系统实现了更有效精确的跟踪。说明相比于PI控制，ARC控制能够主动补偿斗杆、动臂和铲斗执行器的伸缩，在输入值保持不变的情况下，ARC控制可以让挖掘机混合动力系统的倾角快速进入稳定状态，使系统模型的收敛速度更快，具有良好的动力学响应性能。

为了进一步研究控制器的性能，ARC控制和PI控制下系统回转位置和速度的跟踪误差e1、e2，如图6、图7所示。

图6 位置跟踪误差曲线Fig.6 Position Tracking Error Curve

图7 速度跟踪误差曲线Fig.7 Velocity Tracking Error Curve

从图中可以看出，虽然ARC控制和PI控制都会产生位置和速度的跟踪误差，但是PI控制下系统模型会出现较大的位置和速度超调，这说明PI控制并不能很好地补偿系统的非线性。显然，在这两种情况下，ARC控制都能获得更好的控制性能和跟踪性能，且跟踪精度较高。

6 结论

构建了挖掘机液压混合动力系统结构，考虑到系统结构的不确定性，对液压系统、挖掘机动力学和发动机进行建模，在此基础上结合反馈控制实现对系统模型的ARC 控制。最后在Matlab/Simulink环境下对斗杆、动臂和铲斗的倾角进行跟踪仿真实验，给出了系统模型回转位置和速度的跟踪误差，并与PI控制方法进行了比较分析。结果表明，相比于PI控制，ARC控制使系统模型的收敛速度更快，有良好的动力学响应性能，而且能更好地补偿系统模型的非线性，具有更好的控制稳定性和更高的跟踪精度。