下颌第二磨牙近中移动的生物力学分析

闫麒安 周静文 米丛波

[摘 要]目的 通過三维有限元方法探讨不同力值和加力方式下近中整体移动下颌第二磨牙的位移趋势及牙周膜应力分布，以期为临床提供参考。方法 于2023年5月选取新疆医科大学第一附属医院口腔影像科1例患者的锥形束CBCT资料，建立第一磨牙缺失的三维有限元模型。在第二磨牙牙冠上放入不同的矫治装置，通过不同力值（100 g或50 g）及加力方式（近中牵引钩或远中牵引钩）进行分组，共8组工况。使用Abaqus软件模拟比较8组工况近中整体移动下颌第二磨牙的位移趋势及牙周膜应力分布。结果 在所有工况中，牙周膜Von Mises应力最大值均未超过2.6×10-2 Mpa，远中牵引钩的应力分布较近中牵引钩应力分布均匀。当颊侧加力50 g舌侧加力100 g时，第二磨牙颊侧面出现近中平移，近中面出现颊侧旋转，颌面出现向近中偏颊侧的旋转，与根尖组结果基本一致，此时牙周膜Maximum Principal Stress应力分布主要集中在第二磨牙牙周膜远中面。结论 ①近中移动下颌第二磨牙时，远中牵引钩应力分布更均匀；②牵引钩加力100 g舌侧扣加力50 g时，第二磨牙从颊侧面出现向远中旋转移动趋势，可以为矫正倾斜的第二磨牙提供临床参考；③在平齐根分叉远中牵引钩颊侧加力50 g舌侧扣加力100 g情况下，第二磨牙最接近整体近中移动趋势，且应力分布均匀。

[关键词] 下颌第二磨牙；三维有限元方法；应力分布

[中图分类号] R78 [文献标识码] A [文章编号] 1004-4949（2024）06-0037-07

基金项目：国家自然科学基金项目（编号：81960196）

Biomechanical Analysis of Mesial Movement of Mandibular Second Molar

YAN Qi-an， ZHOU Jing-wen， MI Cong-bo

（Department of Orthodontics， the First Affiliated Hospital of Xinjiang Medical University/Affiliated Stomatological Hospital， Urumqi 830054， Xinjiang， China）

[Abstract]Objective To investigate the displacement trend and periodontal stress distribution of the mandibular second molar under different force values and reinforcement methods by three-dimensional finite element method， so as to provide reference for clinical practice. Methods In May 2023， conical beam CBCT data of a patient in the Department of Dental Imaging of the First Affiliated Hospital of Xinjiang Medical University were selected to establish a 3D finite element model of the missing first molar. Different corrective devices were placed on the crown of the second grinding tooth， and the groups were divided by different force values （100 g or 50 g） and additional force methods （mesial traction hook or distal traction hook）， a total of 8 working groups. Abaqus software was used to simulate and compare the displacement trend and the stress distribution of periodontal membrane of the second molar in 8 working conditions. Results The maximum Von Mises stress of the periodontal membrane did not exceed 2.6×10-2Mpa in all conditions， and the stress distribution of the distal traction hook was more uniform than that of the proximal traction hook. When the buccal Stress was 50 g and the lingual stress was 100 g， mesial translation occurred on the buccal side of the second molar， buccal rotation occurred on the mesial side， and the maxillary side rotated to the mesial side， which was basically consistent with the results of the apical group. At this time， the Maximum Principal Stress distribution of the periodontal membrane was mainly concentrated on the distal side of the second molar periodontal membrane. Conclusion ①The stress distribution of the distal traction hook is more uniform when the mandibular second molar is moved mesially； ②When the traction hook is applied 100 g and the lingual buckle is applied 50 g， the second molar appears a trend of distantly rotating movement from the buccal side， which can provide clinical reference for correcting the tilted second molar； ③Under the condition that the buccal force of the distal traction hook is 50 g and the lingual force is 100 g， the second molar is the closest to the overall mesial movement trend， and the stress distribution is uniform.

[Key words] Mandibular second molar； Three-dimensional finite element method； Stress distribution

在正畸学中，第一磨牙是咬合的关键[1]。这颗牙齿在6岁时萌出，并被认为是成年人中最常缺失的牙齿[2，3]。缺失这颗牙齿会引起较多问题，例如相邻牙齿向缺失牙位倾斜、颌牙齿伸长以及颞下颌关节问题[4-6]。临床实践中，在患者下颌第三磨牙牙体形态较好时，正畸医师常会选择优先拔除患牙的原则[7-10]，即拔除病变的下颌第一磨牙、整体近中移动下颌第二磨牙、直立下颌第三磨牙并近中移动，保留完整的牙列[11，12]。有限元（finite element method，FEA）是随计算机技术的发展而兴起的一种现代计算方法[13，14]，能够对载荷、形态、结构和力学性能等较为复杂的构件进行力学分析，具有较强的优越性[15-17]。已经有大量研究将FEA应用于在口腔医学领域[18-21]。本研究旨在分析不同力值和加力方式下近中整体移动的下颌第二磨牙的位移趋势及牙周膜应力分布，以期为临床近中整体移动磨牙提供参考。

1 资料与方法

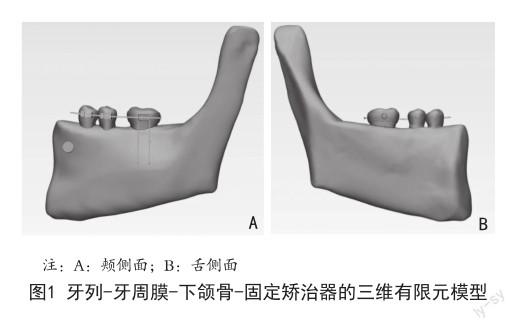
1.1 数据获取及建立三维有限元模型 于2023年5月在新疆医科大学第一附属医院口腔放射科选取1例患者的锥形束CBCT资料。纳入标准：下颌牙列完整；下颌第二磨牙牙根完全形成；牙体健康、无牙体牙髓病、牙周病、无冠部修复体。排除标准：下颌第一磨牙区域有骨缺损者；下颌第一磨牙区域牙槽骨及颌骨区域有病理性损伤或外伤史者；下颌第一磨牙区域影响颌骨识别者；有骨质疏松史、头颈部放疗史及双膦酸盐用药史等其它影响骨质类型及结构者。患者使用新疆疆医科大学第一附属医院口腔放射科三维体层X线影像系统New Tom（意大利，美众亿公司）CBCT扫描获取原始数据。保存文件，文件格式为DICOM格式类型。下颌骨具有左右对称性，因此选取左侧下颌骨升支前缘至左下第一前磨牙近中为研究范围。将DICOM格式的图像文件导入到Mimics 21.0软件中，生成原始三维重建模型，模型保存为STL格式。以STL格式文件输出到Geomagic软件中，采用0.20 mm厚度生成牙周膜。最终建立完整光滑的三维模型，以STP格式输出。导入Solid work 2022软件中进行装配。利用Solid work 2022的建模功能，分别建立标准MBT托槽、带环、牵引钩、舌侧扣、0.017"×0.025"的不锈钢方丝、微种植体模型。以STP格式导入Abaqus 2020软件赋予各部件模型相应材料力学参数及接触关系，设置网格参数，建立静力分析框架（图1）。生成节点数257 249个，单元数146 107个，所有网格类型为四面体型（C3D10）。设定边界条件及加载条件，并计算结果，共建立起了8种工况。

1.2 工况设定 工况1：与根分叉平齐近中牵引钩加力100 g及舌侧扣加力50 g；工况2：与根分叉平齐近中牵引钩加力50 g及舌侧扣加力100 g；工况3：与根尖端平齐近中牵引钩加力100 g及舌侧扣加力50 g；工况4：与根尖端平齐近中牵引钩加力50 g及舌侧扣加力100 g；工况5：与根分叉平齐远中牵引钩加力100 g及舌侧扣加力50 g；工况6：与根分叉平齐远中牵引钩加力50g及舌侧扣加力100 g；工况7：与根尖端平齐远中牵引钩加力100 g及舌侧扣加力50 g；工况8：与根尖端平齐远中牵引钩加力50 g及舌侧扣加力100 g。

1.3 材料属性及边界约束 各材料和组织均为连续、均质、各向同性的线弹性体。弹性模量及泊松比见表1，各材料设定为均质同性的线弹性体。下颌骨为固定约束，种植体支抗与牙槽骨、牵引钩与牙齿、牙齿与矫治器、牙根-牙周膜、牙周膜-牙槽骨间为绑定关系。

2 结果

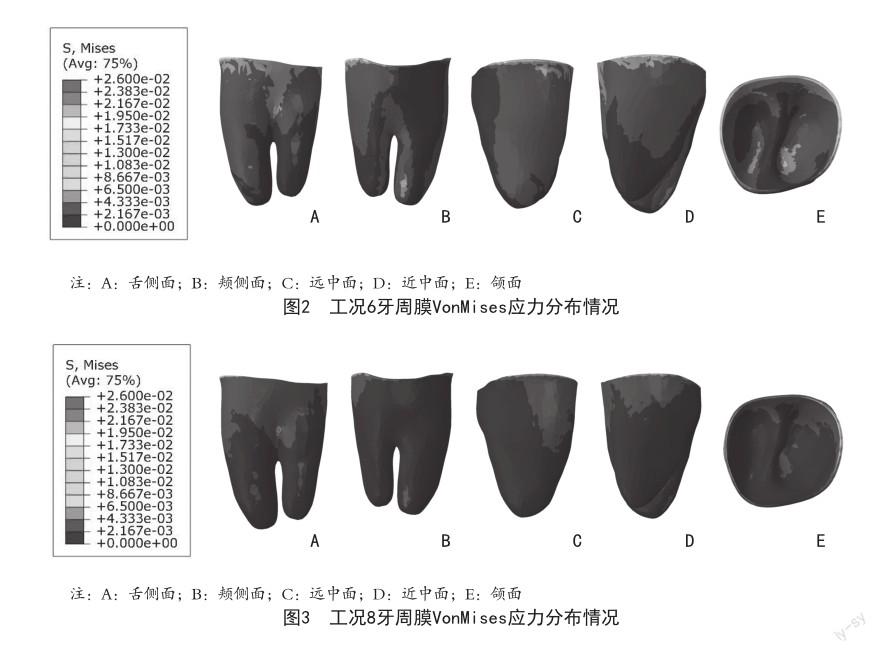
2.1 牙周膜Von Mises应力分布情况 本研究中牙周膜的Von Mises应力分布随着加载力和加力方式的变化而变化，牙周膜Von Mises应力集中区主要在颈部，从颈缘到根尖区应力有逐渐减小的趋势，根尖未见明显应力集中区。根据实验所得结果可知，所有工况应力最大值均未超过2.6×10-2 Mpa，根分叉组远中牵引钩加力50 g舌侧加力100 g时（工况6），第二磨牙牙周膜颈部及根尖应力分布较近中牵引钩更均匀，见图2。根尖组远中牵引钩加力50 g舌侧加力100 g时（工况8），第二磨牙牙周膜颈部及根尖应力分布较近中牵引钩更均匀，见图3。牙周膜Von Mises应力分布最大值见表2。

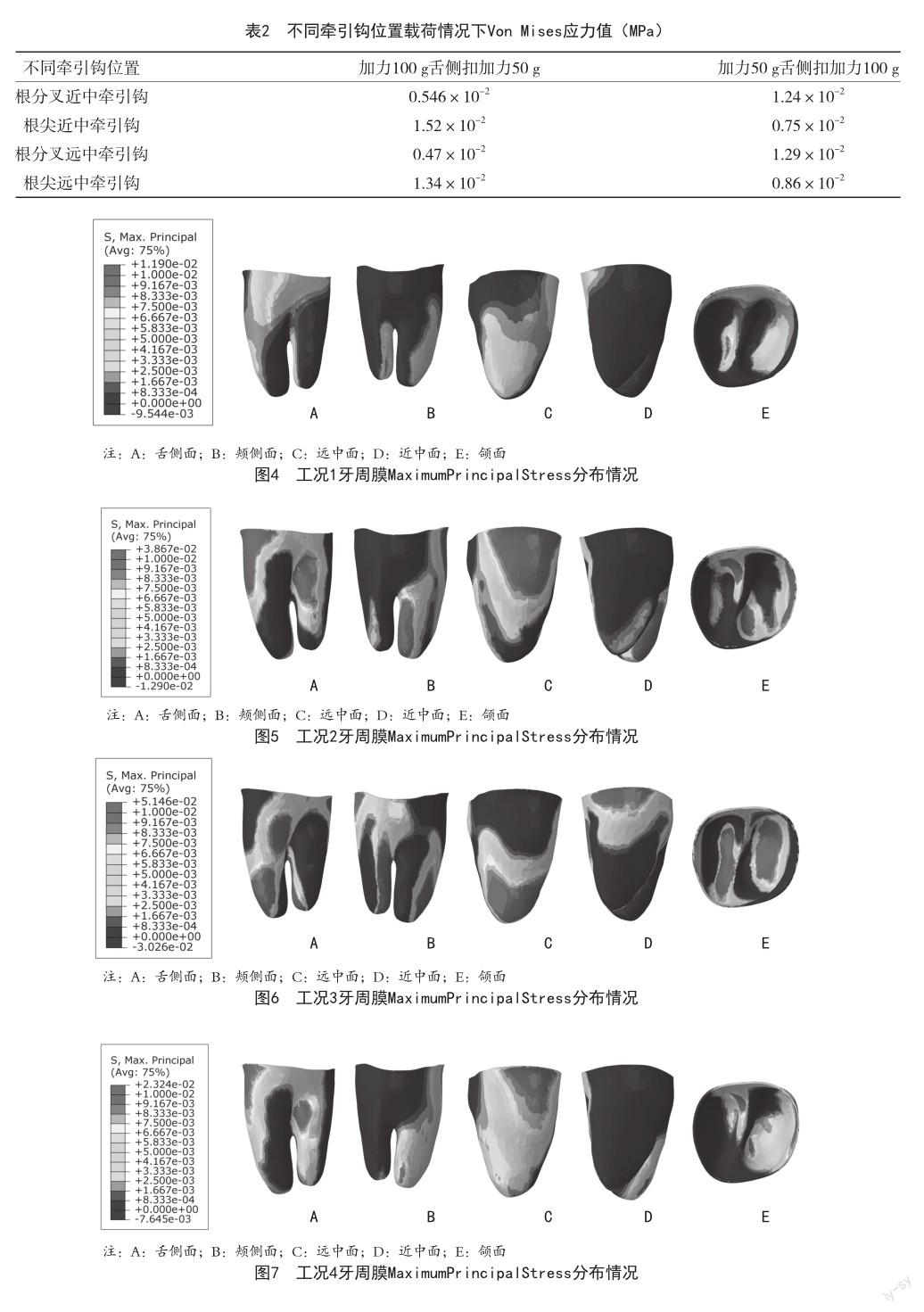
2.2 牙周膜Maximum Principal Stress分布情况 本研究中牙周膜的Maximum Principal Stress表示为正值时为拉应力，体现出受力方向和大小，应力分布随着加载力和加力方式的變化而变化。根据实验所得结果可知，根分叉近中与远中牵引钩加力100 g舌侧加力50 g时（工况1），第二磨牙牙周膜远中面及近中根远中面出现拉应力，应力分布均匀，见图4。当颊侧加力50 g舌侧加力100 g时（工况2），第二磨牙牙周膜远中面及远中根近中面出现拉应力，见图5。根尖组近中与远中牵引钩加力100 g舌侧加力50 g时（工况3），第二磨牙牙周膜近中面牙颈部及近远中根远中面出现拉应力，见图6。当颊侧加力50 g舌侧加力100 g时（工况4），第二磨牙牙周膜远中面牙颈部及近中根近中面出现拉应力，见图7。牙周膜Von Mises应力分布最大值见表3。

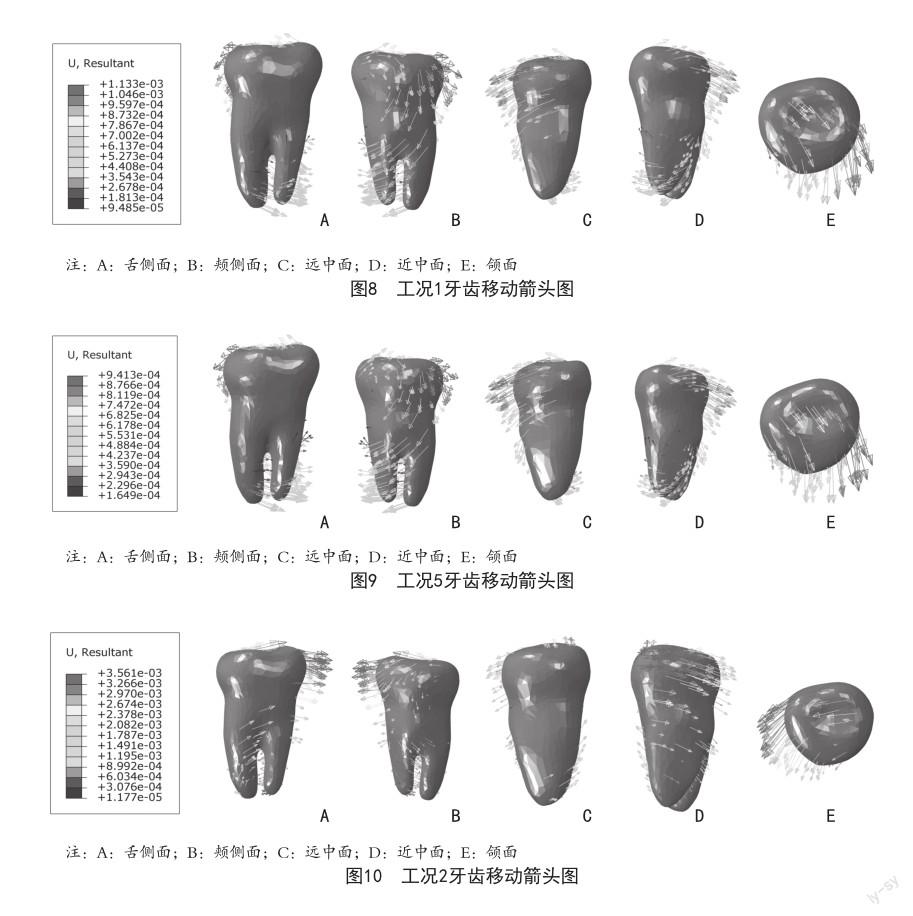
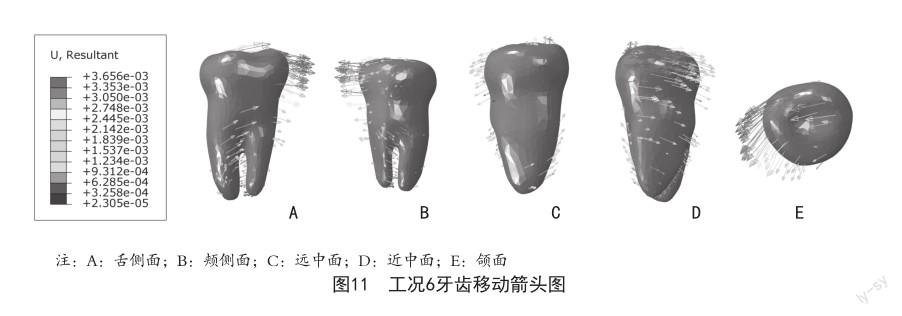
2.3 牙齿位移箭头图 牙齿移动方向随着加载力值和加力方式的变化而变化，牙齿的移动较为复杂，本研究中主要从颊舌方向、近远中方向和颌面方向进行探讨。根据研究所得结果可知，根分叉组颊侧加力100 g舌侧加力50 g时（工况1、工况5），第二磨牙颊侧面出现远中旋转，近中面出现颊侧旋转，颌面出现向远中偏颊侧的旋转，与根尖组结果基本一致，见图8、图9；当颊侧加力50 g舌侧加力100 g时（工况2、工况6），第二磨牙颊侧面出现近中平移，近中面出现颊侧旋转，颌面出现向近中偏颊侧的旋转，与根尖组结果基本一致，见图10、图11。

3 讨论

在正畸治疗过程中，牙周膜应力的调控是一个至关重要的环节[22]。牙周膜作为牙齿与牙槽骨之间的结缔组织，对于保持牙齿的位置和稳定性起着关键作用。通过施加缓和持续的力量，牙周膜形成张力区和压力区，从而引导牙槽骨进行生理性改建。如果施加的力量过大，牙周膜会发生无菌性坏死，即玻璃样变。在这种情况下，牙周膜无法发挥正常的生理功能，导致牙齿的移动速度减缓甚至停滞[23]。更严重的是，压力侧的牙槽骨会发生潜行性吸收，进一步影响牙齿的稳定性[24]。牙周膜应力的大小和分布不但影响着牙齿移动的方式，而且为临床矫治力的评价、选择合适的加力方式提供了量化指标。Lee BW[25]研究提出，牙周应力超过2.6×10-2 Mpa则会超过其强度极限，对牙周产生永久损害。因此，在正畸治疗中，选择合适的力量或力系是至关重要的。

本研究中牙周膜的应力分布随着力值和加力方式的变化而变化，应力集中区的位置也相应改变。第二磨牙牙周膜应力集中区位于在牙颈部，根尖未发现明显应力集中区。有学者[26]利用三维有限元模型对根尖应力进行深入观察，结果发现牙齿在进行整体移动和倾斜移动时，应力主要集中在牙槽嵴周围，而非根尖部分。这一实验模型是基于正常形态的牙齿构建的，其牙根形态正常，根尖圆钝，移动方式也主要为倾斜移动和整体移动。因此，根尖区域并未出现明显的应力集中现象。Huiskes R等[13]研究发现，倾斜运动的牙颈部牙槽骨吸收量大于整体运动，这一发现对于临床工作具有重要的指导意义，提醒医生在矫治过程中需仔细观察牙根形态和牙齿移动方式，以便更精准地选择矫治力，确保矫治过程的安全与效果。此外，本研究也发现，远中牵引钩的应力均小于近中钩加力，在临床设计中应尽可能放置远中牵引钩，并且在双平齐根分叉远中牵引钩颊侧加力50 g舌侧扣加力100 g时，第二磨牙整体近中移动的方向最明显，与国外学者Nihara J等[27]仅研究近中牵引钩设计下磨牙近中移动应力分布结果较一致，并且支抗钉的位置高度对近中整体移动第二磨牙的影响不大。

综上所述，近中移动下颌第二磨牙时，远中牵引钩应力分布更均匀；牵引钩加力100 g舌侧扣加力50 g时，第二磨牙从颊侧面出现向远中旋转移动趋势，可以为矫正倾斜的第二磨牙提供临床参考；在平齐根分叉远中牵引钩颊侧加力50 g舌侧扣加力100 g情况下，第二磨牙最接近整体近中移动趋势，且应力分布均匀。

[參考文献]

[1]Miclotte A，Grommen B，Cadenas de Llano-Pérula M，et al.The effect of first and second premolar extractions on third molars： A retrospective longitudinal study[J].J Dent，2017，61：55-66.

[2]Müller F，Naharro M，Carlsson GE.What are the prevalence and incidence of tooth loss in the adult and elderly population in Europe？[J].Clin Oral Implants Res，2007，18 Suppl 3：2-14.

[3]Corraini P，Baelum V，Pannuti CM，et al.Tooth loss prevalence and risk indicators in an isolated population of Brazil[J]. Acta Odontol Scand，2009，67（5）：297-303.

[4]Hatami A，Dreyer C.The extraction of first， second or third permanent molar teeth and its effect on the dentofacial complex[J].Aust Dent J，2019，64（4）：302-311.

[5]Baik UB，Choi HB，Kim YJ，et al.Change in alveolar bone level of mandibular second and third molars after second molar protraction into missing first molar or second premolar space[J].Eur J Orthod，2019，41（5）：513-518.

[6]Hong H，Zhou J，Fan Q，et al.Characteristics of Spatial Changes in Molars and Alveolar Bone Resorption among Patients with Loss of Mandibular First Molars： A CBCT-Based Morphometric Study[J].J Clin Med，2023，12（5）：1932.

[7]Chen HH，Chen G，Su H.Orthodontic treatment of substituting third molars for missing permanent molars[J]. Am J Orthod Dentofacial Orthop，2023，163（2）：173-180.

[8]Park JH，Kim KW，Lee NK，et al.The effects of a corticotomy on space closure by molar protraction using TSADs in patients with missing mandibular first molars[J]. OrthodCraniofac Res，2022，25（2）：159-167.

[9]Cardoso PC，Mecenas P，Normando D.The impact of the loss of first permanent molars on the duration of treatment in patients treated with orthodontic space closure and without skeletal anchorage[J].Prog Orthod，2022，23（1）：32.

[10]Wu JC，Zheng YT，Dai YJ.Protraction of mandibular molars through a severely atrophic edentulous space in a case of juvenile periodontitis[J].Korean J Orthod，2020，50（2）：145-154.

[11]Nguyen T，Baek ES，Hwang S，et al.Nonsurgical and nonprosthetic camouflage treatment of skeletal Class II open bite with bilaterally missing lower first molars[J]. Angle Orthod，2019，89（3）：505-517.

[12]Kim SJ，Sung EH，Kim JW，et al.Mandibular molar protraction as an alternative treatment for edentulous spaces： Focus on changes in root length and alveolar bone height[J].J Am Dent Assoc，2015，146（11）：820-829.

[13]Huiskes R，Chao EY.A survey of finite element analysis in orthopedic biomechanics： the first decade[J]. Biomech，1983，16（6）：385-409.

[14]Welch-Phillips A，Gibbons D，Ahern DP，et al.What Is Finite Element Analysis？[J].Clin Spine Surg，2020，33（8）：323-324.

[15]Cortona A，Rossini G，Parrini S，et al.Clear aligner orthodontic therapy of rotated mandibular roundshaped teeth：a finite element study[J].Angle Orthod，2020，90（2）：247-254.

[16]Revilla-León M，Gómez-Polo M，VyasS，et al.Artificial intelligence applications in implant dentistry： A systematic review[J].J Prosthet Dent，2023，129（2）：293-300.

[17]Cattaneo PM，Cornelis MA.Orthodontic Tooth Movement Studied by Finite Element Analysis： an Update. What Can We Learn from These Simulations？[J].Curr Osteoporos Rep，2021，19（2）：175-181.

[18]Paetyangkul A，Türk T，Elekda？-Türk S，et al.Physical properties of root cementum： part 14.The amount of root resorption after force application for 12 weeks on maxillary and mandibular premolars： a microcomputedtomography study[J].Am J Orthod Dentofacial Orthop，2009，136（4）：491-499.

[19]Zhang X，Li MQ，Guo J，et al.An analysis of the optimal intrusion force of the maxillary central incisor with root horizontal resorption using the finite element method and curve fitting[J].Comput Methods Biomech Biomed Engin，2022，25（13）：1471-1486.

[20]Zhang Y，Gao J，Wang X，et al.Biomechanical factors in the open gingival embrasure region during the intrusion of mandibular incisors： A new model through finite element analysis[J].Front Bioeng Biotechnol，2023，11：1149472.

[21]Kawamura J，Park JH，Kojima Y，et al.Biomechanical analysis for total mesialization of the mandibular dentition：A finite element study[J].OrthodCraniofac Res，2019，22（4）：329-336.

[22]Roscoe MG，Cattaneo PM，Dalstra M，et al.Orthodontically induced root resorption： A critical analysis of finite element studies input and output[J].Am J Orthod Dentofacial Orthop，2021，159（6）：779-789.

[23]Reitan K.Clinical and histologic observations on tooth movement during and after orthodontic treatment[J].Am J Orthod，1967，53（10）：721-745.

[24]劉海君，杨琳，杨凯，等.不同力值对正畸牙移动压力侧破骨细胞活性的影响[C]//中华口腔医学会口腔正畸专业委员会.2016中国国际正畸大会暨第十五次全国口腔正畸学术会议论文汇编.2016：2.

[25]Lee BW.Relationship between tooth-movement rate and estimated pressure applied[J].J Dent Res，1965，44（5）：1053.

[26]Oyama K，Motoyoshi M，Hirabayashi M，et al.Effects of root morphology on stress distribution at the root apex[J]. Eur J Orthod，2007，29（2）：113-117.

[27]Nihara J，Gielo-Perczak K，Cardinal L，et al.Finite element analysis of mandibular molar protraction mechanics using miniscrews[J].Eur J Orthod，2015，37（1）：95-100.

收稿日期：2024-02-20 编辑：周思雨