解析几何中的距离和、差的最值问题

徐满红

【摘 要】  解析几何中距离和差的最值问题是用几何的方法研究代数，数与形的有效结合，蕴含着丰富的数学思想方法.

【关键词】  距离和;距离差;核心素养.

1  纵向联系

回顾初中学习的将军饮马问题.

方法总结  （1）关注定点与直线的位置关系，对于线段之和，将定点转换到直线的异侧，而对于线段之差，需将两定点转换到直线的同侧.两条线段的和与差的最值状态均是三点共线；

2  横向比较

2.1  圆锥曲线

类型1  两定点在圆锥曲线的同侧

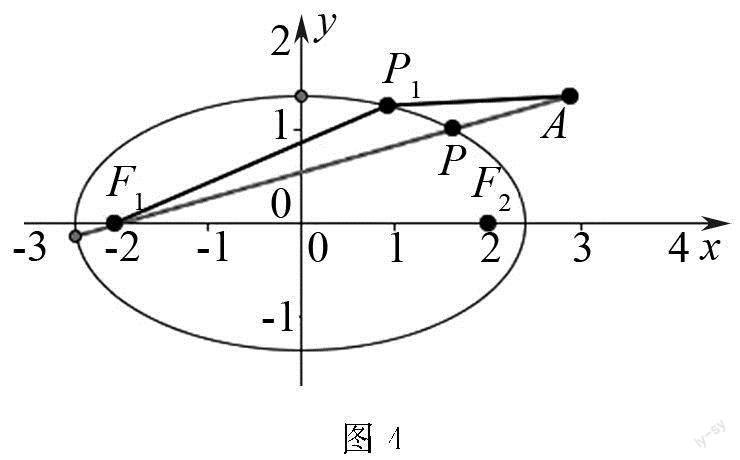
分析  线段和最短问题，如果能将两个定点放到曲线的两侧，问题就会变得很简单.因此，联系将军饮马问题的解决方法，我们思考的重点就變成了如何将其中一个定点转换到曲线的另一侧.但是，曲线无法做对称，而椭圆作为一个封闭的图形，两个焦点都在椭圆的同一侧，可以利用椭圆定义（椭圆上的点到两焦点距离之

分析  对于线段之差最值问题，两个定点又在曲线的同侧，问题就会变得很简单，三点共线就能解决线段差的最值问题.

分析  此类问题最显著的特征是动点与焦点

类型2  两定点在圆锥曲线的异侧

方法总结  （1）若两线段前系数相同，直接求解或利用椭圆（或双曲线、抛物线）的定义进行适当转化后求解.

若两线段前系数不同，利用圆锥曲线的统一定义，将圆锥

曲线上的动点到焦点的距离与到相应准线的距离进行互化后，达到系数一致再求解.

2.2  圆

解法1  相似三角形

解法2  尼斯圆定义转换

评析  解析几何中距离和差的最值问题是用几何的方法研究代数，数与形的有效结合，蕴含着丰富的数学思想方法，方法灵活，综合性强，难点大，是培养学生数学运算、逻辑推理、数学抽象、直观想象等核心素养的重要载体.能够形成高级思维，培养逻辑化，批判性地多方面思考问题的能力.

本专题小切口，深层次，通过纵向联系，横向比较，通过对问题进行的垂直变式【1】，多题一解，多题归一，使解决问题的思维水平呈直线型向纵深发展，不仅使学习者完成知识从局部到整体，从单一到多元，从简单到复杂的提升，也使数学思维从肤浅达到了深刻，是逻辑体系的教学.

参考文献：

[1]郑东辉.促进深度学习的课堂评价：内涵与路径[J].课程·教材·教法，2019，39（02）：59-65.

[2]郭华.深度学习及其意义[J].课程·教材·教法，2016，36（11）：25-32.

[3]曾家延，董泽华.学生深度学习的内涵与培养路径研究[J].基础教育，2017（4）：59-67.

[4]张奠宙.中国数学双基教学[M].上海：上海教育出版社.2006.

[5]吴从峰.论中学数学的艺术性[J].江西教育学院学报，2010，31（06）：65.