如何理解“求捆瓶子中绳长”问题中的圆弧拼合部分

颜丽霞

《教学月刊·小学版》（数学）2023年第10期刊登了《如何更好地解决“求捆瓶子中绳长”问题》一文，该文有许多可圈可点之处。然而，文章在求捆三个圆柱形瓶子的绳长（如图1）时，选择直接告诉学生三角形的每个内角为60°，三角圆弧所对应的圆心角为120°，这一做法存在一定的问题。经笔者研究发现，许多学生在理解如何确定三角形每个内角为60°以及每条圆弧所对应的圆心角为120°等方面存在困难。此外，理解“三条圆弧的长度之和等于一个圆的周长”这一规律，对学生来说也有较大难度。为帮助学生解决这些难点问题，可以采用以下教学过程。

一、动态感知，想象移拼

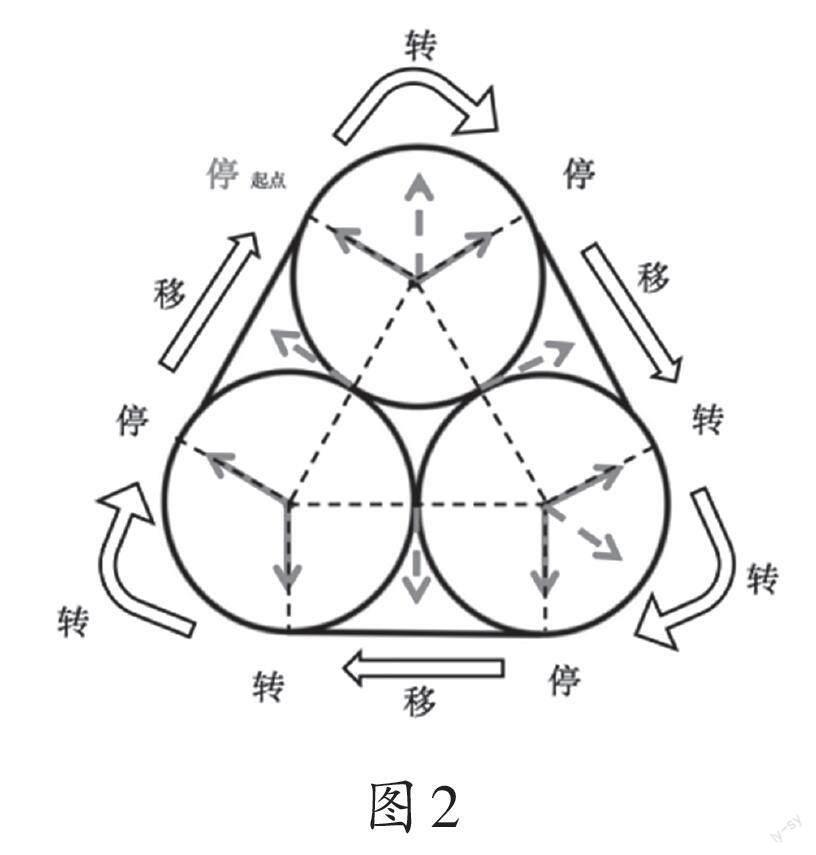
教师呈现示意图（如图2），要求学生自主操作，用笔尖代替图中的箭头，从起点开始转一周，描出捆三个圆柱形瓶子的绳长，边描边思考，圆弧部分拼成了什么图形？

学生独立完成操作后反馈：笔尖从起点出发，沿着箭头转一周，发现笔尖所经过圆弧部分的路径恰好為一个圆形。因此，圆弧部分拼起来的长度正好为圆的周长。

二、画图表征，推理说明

教师出示图3，让学生独立尝试画分割线。

学生独立尝试后，教师直观演示画图方法：将相邻两个圆的圆心连接，得到一条线段。分别通过这两个圆心作这条已知线段的垂线（即圆的半径），并连接半径与圆相交的两点，从而得到绳子的线段部分，从而将绳子分为圆弧和直线两部分（如图1）。

接着引导学生思考：（1）连接相邻两个圆的圆心所形成的线段长度是多少？（2）圆弧部分有什么特点，拼起来是什么图形？

学生独立思考后，进行全班交流。

（1）观察经分割后的线段，连接相邻两个圆的圆心所形成的线段由两条半径构成，其长度相当于一个圆的直径。

（2）图1中，三个圆的圆心两两相连，构成三条线段。这三条线段长度相等，形成了一个等边三角形，每个内角均为60°。

（3）在分割过程中，通过圆心作圆心连线的垂线，夹角为90°。因此，绳子的线段部分、相邻两个圆心间的连线以及两条垂线（即圆的两条半径）共同构成一个长方形，内角为90°。

根据以上信息，可以推断每个圆内圆弧部分所对的圆心角为：360°-90°-90°-60°=120°。因此，每段圆弧的长度为一个圆周长的[13]，即120°÷360°=[13]。分割后有三段圆弧，合起来恰好是一个圆的周长。

（浙江省杭州市临平区崇贤第一小学）