运算方法迁移的应然思考

于正军

【摘   要】感悟數的运算本质上的一致性，不只是让学生简单地实现计算方法的迁移和自主尝试，还要从学生的“数学现实”出发，设计符合学生学习的认知思维的应然过程，使学生经历竖式书写、理解算理、掌握算法的学习过程。教学时，教师要引导学生经历“零起点”的认知过程、“裸视图”的思维过程以及“应变化”的内化过程，促使学生在知识形成过程中主动参与、自主探究，进而真正感悟数的运算的本质内涵，建立算理的联系，形成算法的迁移，体会数的运算本质上的一致性，实现学生核心素养和关键能力的协同发展。

【关键词】数学现实；运算方法；思维迁移；一致性

根据《义务教育数学课程标准（2022年版）》的要求，在进行“数与运算”主题的教学时，要让学生经历算理和算法的探索过程，理解算理，掌握算法，从而感悟数的运算以及运算之间的关系，体会数的运算本质上的一致性。感悟数的运算本质上的一致性，不只是让学生简单地实现计算方法的迁移和自主尝试，还要从学生的“数学现实”出发，设计符合学生学习的认知思维的应然过程，使学生经历竖式书写、理解算理、掌握算法的学习过程。因此，教师教学时，要引导学生经历“零起点”的认知过程、“裸视图”的思维过程以及“应变化”的内化过程，促使学生在知识形成过程中主动参与、自主探究，进而真正感悟数的运算的本质内涵，建立算理的联系，形成算法的迁移，体会数的运算本质上的一致性，实现学生核心素养和关键能力的协同发展。本文以苏教版教材一年级下册第四单元的“两位数加、减两位数（不进位、不退位）”的教学内容为例，从学生的“数学现实”视角探讨数的运算本质上的一致性。

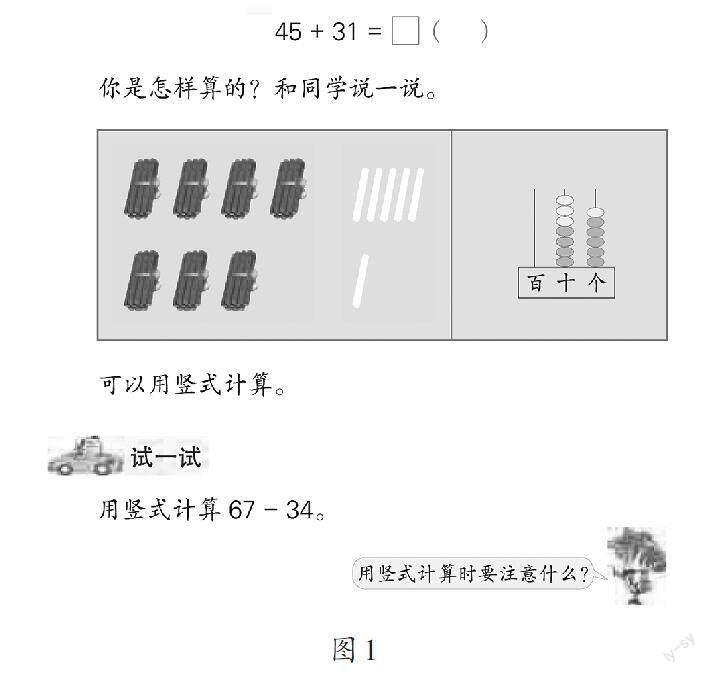
教材采用乘车情境图引入加法算式45+31（如图1），引导学生自主探索两位数加两位数的计算方法，力求借助小棒图和计数器，启发学生通过直观观察或动手操作理解算理、掌握算法。在教学67-34时，教材则直接采用“试一试”的方法，让学生独立进行计算。教师若直接按照教材的编排结构进行教学，不但无法推进学生体会加、减法运算之间的联系以及数的运算本质上的一致性，还会影响学生对减法算理的积极探索和对减法算法的自主建构。这是因为减法运算中摆小棒和拨计数器的活动所蕴含的算理在思维水平的要求上要明显高于加法运算，仅仅依靠主题图中加法算理提供的直观图式，无法实现从加法运算向减法运算的思维迁移。因此，加、减法运算间的思维迁移应从学生的认知现实出发，针对加、减法运算的竖式书写、算理探索及算法应用展开“现实化”的学生实践，促进他们对加、减法运算本质上的一致性的体会与感悟。

一、竖式书写的“数学现实”一致性：需要经历“零起点”的认知过程

“零起点”认知指学生尚未接触新知领域时的思维认知状态。在“两位数加、减两位数（不进位、不退位）”的笔算教学中，学生首次接触竖式的概念，其书写应呈现“零起点”的认知状态。计算教学固然要以学生的认知发展水平和已有知识经验为基础，但新概念的自然生长还依赖于学生的“零起点”认知，以促进基于“数学现实”的运算概念的建构，从而帮助学生实现对概念的理解。可见，计算教学的“零起点”认知过程，是一种基于计算知识的结构性、生长性和应用性的学生认知活动，凸显学生对已有知识的再建构、已有经验的再利用以及已有认知的再突破，以使学生体会竖式书写本质的一致性。

（一）激活学生经验，激发自主思维

教师创设“45+31怎样算”的自主交流活动，激活学生经验，激发学生思考：两个数相加除了写成横式进行计算，还可以如何书写？教学时，教师应引发学生的认知冲突，鼓励他们大胆尝试并表达自己的想法。只有借助竖式书写的创造过程，学生才能充分暴露竖式书写过程中的意图、想法及问题。这也为学生规范、正确地书写竖式积累认知经验、奠定思维基础，有效避免机械地要求学生模仿教材中的“可以用竖式计算”的灌输式教学方法，有助于学生主动体会和理解竖式计算与竖式书写的意义、价值及效用。

（二）引发直观思维，生发知识经验

在教学过程中，教师基于学生认知方式的“数学现实”，引导学生自主构建竖式计算的过程。

师：竖式应该如何书写呢？45加31，应先写哪个数？再写哪个数？

生：先写45，再写31。

生：45和31要上下对齐。

师：那“加31”中的加号写在哪里？

生：写在31的前面。

师：为什么？

生：因为在横式计算中，加号写在31的前面，所以在竖式计算中，加号也要写在31的前面。

上述教学过程揭示了学生对竖式书写格式现实意义的建构，体现了学生与成人理解上的差异。

（三）启发学生认知，启迪数学感悟

教师在学生认知的基础上构建竖式书写的意义，引导学生进一步理解竖式计算的作用和价值。

师：你们觉得相加的两个数是竖向书写成竖式还是横向书写成横式更合适呢？

（学生在课堂上纷纷发表意见，观点各异）

生：横式写起来方便，且不占用过多位置。

生：竖式计算更为简便。

师：为什么用竖式更简便？

生：在横式中，两位数加两位数有时可能难以直接口算出结果或容易算错。而在竖式中，我们可以分别计算每个数位上的和，这样只需计算一位数加一位数就可以了。

上述教学过程引导学生经历“零起点”的认知过程，并开展相关的探究、讨论和交流，使学生体会横式计算和竖式计算的异同，初步感知两种书写形式隐含的算理和算法的联系与区别。同时，借助加法竖式的计算过程，使学生深刻感悟到，无论是横式书写还是竖式书写，其计算过程表示的都是小棒图中整捆与整捆、单根与单根的相加，进而进一步认识到横式计算与竖式计算运算本质上的一致性。

二、算理理解的“数学现实”一致性：需要经历“裸视图”的思维过程

“裸视图”的思维过程指基于学生“数学现实”的算理“可视化”过程。这种思维方式使学生能够在静态思维中自然感知计算算理，在动态思维中自主感悟计算算理，从而实现加、减法计算算理的理解与意义建构，推动加法运算向减法运算的自然迁移，初步感悟加、减法运算本质上的一致性。

教师借助图1中的小棒图，引导学生把4捆和5根小棒与3捆和1根小棒看作一个整体，用整体的数学眼光观察现在一共有多少根小棒。学生通过观察、思考，在头脑里自然地把整捆与整捆合并、单根与单根合并，直观地看出小棒的总数，从而初步感悟加法的算理，即相同计数单位数量的累加。然而，减法运算无法像加法运算那样直接从静态的小棒图中感悟算理，从而限制了学生对计算方法的自主建构。因此，能表示67-34算理的直观图，需要在小棒图中表示“原有67根小棒，去掉34根小棒，还剩33根小棒”的动态过程，引导学生动手操作或动态演示，以暴露他们的认知思维过程。只有开展这样的数学探究，才能满足学生的认知需求和情感需求，激发他们主动参与计算算理的探索过程，从而感悟减法运算与加法运算在计算方法上的本质一致性。

观察、分析学生探索45+31的算理和算法的过程可以发现，若机械地遵循教材“试一试”中的教学方式，直接要求学生独立计算67-34，并不符合学生的学习基础，且违背知识迁移的认知规律。此外，加、减法的运算意义在学生的认知思维中存在差异。加法表示把两个分量合并成一个总量，即把两个数合并成一个数的运算叫作加法。教师在教学加法时，只要在学生面前直观地呈现两个分量，他们就能够直接感知总量的客观存在。减法表示从总量中去掉一分量求另一分量，即已知两个数的和与其中一个加数求另一个加数的运算叫作减法。教师在教学减法时，若静态展示总量，学生无法直接感知“去掉量”与“剩余量”两个分量的直观存在，导致减法算理的思维视图无法自然“裸露”与直观呈现，要通过动态演示或动手操作才能直接感知。

因此，要让学生形成对加、减法运算一致性的理解与感悟，应从学生的思维现实和运算方法的迁移现实出发，基于“数学现实”对教材的编排结构进行重组，引导学生经历理解加、减法算理的过程。只有通过动手操作小棒或数珠，经历“正向”与“反向”的运算过程，学生才能直接感知诸如小棒“整捆”或“单根”合并、去掉的运算过程，体会加、减法运算之间的内在联系，理解加、减法运算本质上的一致性。

三、算法建构的“数学现实”一致性：需要经历“应变化”的内化过程

“应变化”的内化过程指学生对运算算理和算法的再加工、再认知过程。在计算过程中，由于运算类型发生变化，学生对算理的理解和算法的运用会出现认知上的“缺口”。而要突破这些“缺口”，学生需要基于自身的“数学现实”，对计算方法进行迁移。只有在不同类型的运算中经历“应变化”的内化过程，学生才能对某一运算的算理和算法形成意义建构，将对数的运算本质上的一致性的感悟内化为自身认知，形成“数学化”理解。

“两位数加、减两位数（不进位、不退位）”的教学内容不仅首次引入了竖式计算，还涵盖“两位数与一位数、整十数相加减”的笔算内容。在竖式计算中，学生需要通过不同类型的运算理解和掌握竖式书写、计算方法等运算概念，并在不同情境中实现迁移和内化，从而形成计算技能。

为促进学生对加法笔算的算理理解和算法掌握，在学生探究了两位数加两位数这一计算类型后，教师应启发他们将习得的方法迁移运用至其他计算类型中。例如，基于45+31的竖式计算，教师可引出45+30、30+45、45+3、3+45等“两位数与整十数、一位数相加”的计算类型，进而引导学生探索两位数加整十数或一位数的竖式书写和计算法则。其中，两位数与一位数相加的竖式计算是学困生学习的难点。在计算45+3、3+45时，学生会形成“数位如何对齐？没有数和十位上的4相加，它应该如何算、如何书写？”等认知“缺口”。对于这些在计算过程中自然生成的问题，教师应及时引导学生基于“数学现实”进行数学探究，理解其数学意义。可以說，每一种计算类型对学生而言都是一次新的思维探索与认知突破，学生唯有经过自主探索、合作交流以及同伴引导的思维过程，才能实现计算方法的自然迁移和内化应用。

对于减法运算中的不同计算类型，教师同样需要引导学生对其进行意义建构和方法探究，感悟其计算方法的一致性。例如，由减法计算67-34可衍生出67-60、67-7等“两位数减整十数、一位数”的计算类型，其中皆隐含一定的认知“缺口”。如：计算67-7时，数位如何对齐？个位上减下来的0需要不需要写？计算67-60时，十位上减下来的0需要不需要写？从这些不同计算类型中衍生出来的“应变化”的计算技能，既是学生对计算方法的一次新的认知突破，又是学生自主内化计算方法的过程。这种“应变化”的内化过程是学生理解算理、掌握算法的认知难点，教师理应引领学生在课堂上进行自主探究、独立感悟。

综上所述，学生只有经历运算中不同计算类型的“应变化”过程，才能应对计算中所生成的竖式书写、数位对齐等问题，从而逐步理解算理，掌握算法和抽象法则，从单一的计算思维走向多元的运算思维，实现计算方法的内化与应用。因此，教师应从学生的“数学现实”出发，鼓励学生在不同的计算类型中迁移应用计算方法，使学生在经历“应变化”的内化过程中，进一步感悟计数单位在运算中的作用，感悟运算的一致性。

总之，数学教学应遵循学生的已有知识与思维习惯，避免放任学生随意尝试。只有依据学生的认知基础，跨越学生的“数学现实”，才能实现计算方法的有效迁移。虽然学生可以在教师的指导或外部的帮助下学会“两位数加、减两位数（不进位、不退位）”的知识，但他们在内心深处难以理解和感悟学习“两位数加、减两位数（不进位、不退位）”的数学思想方法。这一现象导致学生仅知其然，却不知其所以然，偏离了发展学生核心素养的教学目标，阻碍了核心素养导向下的教学改进，违背了学生的自主发展和数学知识发生、发展的规律。因此，教师需要在运算概念本质内涵的感悟、思维方法的启发以及学生经验的积累方面，引导学生经历基于“数学现实”的认知过程，使学生真正积累经验、形成方法、感悟思想，从而在课堂上实现知识掌握和素养发展的目标。

（江苏省扬州市江都区实验小学）