比例电磁阀内置式CDC减振器设计与验证
2024-04-25丁二名戴开宇
丁二名,戴开宇
(1.蒂森克虏伯普利斯坦汽车零部件(上海)有限公司,上海 200122; 2.江苏大学 机械工程学院,江苏 镇江 212013)
引言
自2016年以来,在全球能源紧张和国内“双碳”政策的驱动下,新能源电动汽车在全球范围内取得了较快的发展,悬架系统电控化也成为继电动助力转向[1-3]、电动助力制动[4-6]后推动汽车底盘电动化[7-9]
的又一大助力。连续阻尼可调(Continuously Damping Control,CDC)减振器是电控悬架系统[10]的重要配置之一,能够结合不同的上层控制逻辑及策略[11-12],持续的改变悬架系统的阻尼,为整车的舒适性提供更多的乘坐场景体验,同时对车辆的操稳性和安全性提供更为强大的保障[13-14]。CDC减振器从原理上可分为流体黏度可调和节流口可调两大类[15-17]。流体黏度可调减振器主要有磁流变液和电流变液两种形式,主要依靠电磁或电流来控制油液的黏度持续变化以达到阻尼调节的功能,但此类技术对油液的物性可控性要求较高,对电磁或电流的控制要求也较高,因此,制作成本非常高,无法在常规车辆中进行普及。节流口连续可调减振器是在常规减振器的基础上集成一个调节阀口流量或压力的比例电磁阀,来实现阻尼范围的扩展[18-20]。其相对流体黏度可调减振器在技术成熟度和成本上具有较大的经济优势,已开始逐渐向中低端车型的电控底盘悬架系统推广。
本研究介绍一种比例电磁阀内置式CDC减振器,对其内部结构及工作时的油液流动方向进行分析,通过参数化建模获得其阻尼可调范围,并通过实物样件制作和试验来验证理论模型的正确性,为该CDC减振器的开发研究和整车调校应用提供理论指导。
1 结构及工作原理
1.1 减振器结构
如图1所示为所设计电磁阀内置式CDC减振器的机械结构简图,主要由外管、内管、底盖、底阀总成及活塞杆总成组成。其中,底阀总成主要包含底阀阀体及上下两侧的补偿阀和压缩阀; 活塞杆总成包含活塞杆、活塞、复原阀、流通阀、可调阀组1/2及起到调节功能的比例电磁阀总成。电磁阀总成被集成固定在活塞杆的腔体内,并配置相应的滑片阀门与其衔铁相连。活塞将内管内的空间隔离为上侧的复原腔和下侧的压缩腔,底阀处于内管的最下端,与内管、外管之间的空间形成储油腔。
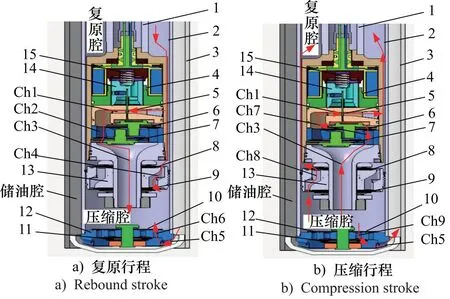
1.活塞杆 2.内管 3.外管 4.电磁铁 5.滑片阀门 6、7.可调阀组1/2 8.流通阀 9.复原阀 10.补偿阀 11.压缩阀 12.底阀阀体 13.活塞 14.衔铁 16.复位弹簧
1.2 工作原理
如结构图1a中的箭头线所示,当减振器处于复原行程时,活塞杆相对于内管向上运动,复原腔的容积变小,其内的油液经过活塞杆壳体和内管外壁间的径向间隙后由两路流到压缩腔:一路是经过流道Ch1,Ch2和流道Ch3,而且该路油液要分别要经过滑片阀门和可调阀组2以形成所需的阻尼;另一路则经过活塞流道Ch4,并要经过复原阀以形成相应的阻尼。而随着压缩腔的容积变大,储油腔内的油液经过底阀阀体上流道Ch5和Ch6补充到压缩腔中,此路的油液要穿过补偿阀以产生相应的阻尼。
如结构图1b中的箭头线所示,当减振器处于压缩行程时,活塞杆相对于内管向下运动,随着压缩腔容积的减小,油液经过两路流到复原腔:一路为经过流道Ch3,Ch7和Ch1,此路需要穿过可调阀系1和滑片阀门形成必要的阻尼;另一路则经过活塞上流道Ch8,此路会穿过流通阀形成相应的阻尼。同时,还有一部分压缩腔中的油液通过底阀阀体中的流道Ch9和Ch5后进入储油腔,该路油液穿过压缩阀形成相应的阻尼。
图2所示为其中的滑片阀门及其对应阀体的截面示意图。滑片阀门在比例电磁铁的吸力和复位弹簧力的双重作用下沿着静铁芯内壁作轴向往复运动,并且可以在有效行程内的任意位置停留。因此,滑片阀门的节流窗口与阀体流道窗口重合部分所形成的节流口面积随着激励电流的连续变化而变化,来实现节流口流量压差的持续调节,达到对减振器阻尼的连续控制。
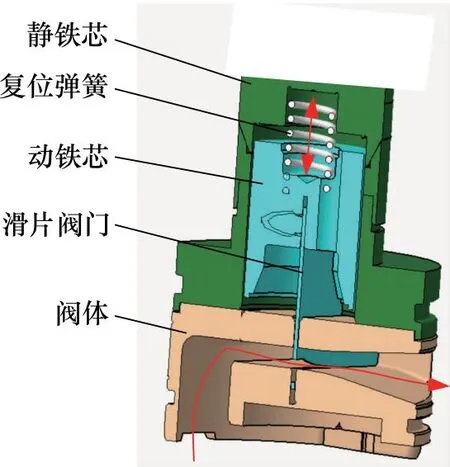
图2 滑片阀门结构设计
2 数模模型
2.1 复原行程建模
根据对该CDC减振器工作原理的分析,拟定其对应的液压原理图。图3a 所示为复原行程时减振器油路的等效液压原理图。从复原腔和储油腔流入压缩腔的油液流量Q12和Q32可分别表示为:
(1)
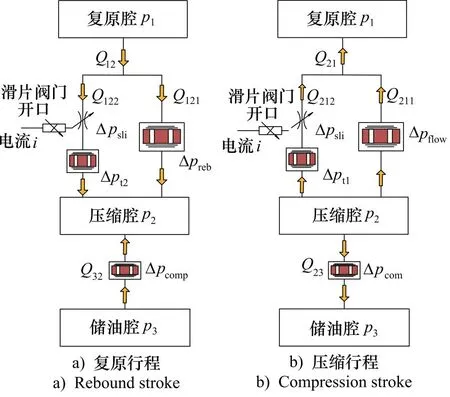
图3 等效液压原理图
式中,Ap,Ar——活塞和活塞杆的截面面积,m2
vr——活塞杆复原行程的速度,m/s
流经滑片阀门的压降可表示为:
(2)
式中,Cd——阀口流量系数
ρ——油液密度,kg/m3
Q122——流经滑片阀门的流量,m3/s
Asli——滑片阀门节流口面积,m2
流经可调阀组2的压降表示为:
(3)
式中,At2——可调阀组2的节流口面积,m2
流经复原阀的压降表示为:
(4)
式中,Q121——流经复原阀的流量,m3/s
Areb——复原阀节流口面积,m2
根据液压油路的串并联原理有:
(5)
联立式(1)~式(5),可求得:
(6)
(7)
(8)
其中,Asli是滑片阀门的节流口面积,由比例电磁铁行程及滑片阀门节流口形状决定,此处表示为:
(9)
式中,x——电磁铁实际行程,m
f(x)——滑片节流口形状函数,m
流经补偿阀的压降可表示为:
(10)
式中,Q32——流经补偿阀流量,m3/s
Acomp——补偿阀节流口面积,m2
储油腔压力可表示为:
(11)
式中,pg0,pg——初始充气压力和动态气体压力,Pa
Vg0——初始充气体积,m3
复原行程的阻尼力可表示为:
Freb=(Ap-Ar)Δpreb+ArΔpcomp-Arp3
(12)
将式(8)、式(10)和式(11)代入式(12),可求解获得该CDC减振器复原行程的阻尼力值。
2.2 压缩行程建模
图3b所示为压缩行程时减振器油路的等效液压原理图。从压缩腔流入到复原腔和储油腔的油液流量Q21和Q23可分别表示为:
(13)
式中,vc——活塞杆压缩速度,m/s
流经可调阀组1的压降为:
(14)
式中,Q212——流经可调阀组1的流量,m3/s
At1——可调阀组1的节流口面积,m2
此时流经滑片阀门的压降变为:
(15)
流经流通阀的压降为:
(16)
式中,Q211——流经流通阀的流量,m3/s
Aflow——流通阀的节流口面积,m2
同样,根据液压油路的串并联原理有:
(17)
联立式(13)~式 (17),可求得:
(18)
(19)
(20)
通过压缩阀的压降为:
(21)
此时储油腔压力可表示为:
(22)
式中,Q23——流经压缩阀的流量,m3/s
Acom——压缩阀的节流口面积,m2
压缩行程的阻尼力可表示为:
Fcom=(Ap-Ar)Δpflow+ArΔpcom+Arp3
(23)
将式(8)、式(10)和式(11)代入式(12),可求解该CDC减振器复原行程的阻尼力值。
3 仿真与实验
3.1 仿真参数设置
依照前面所述的分析过程,利用Simulink软件搭建该CDC减振器的阻尼力仿真模型。如图4a所示为对应仿真模型,图4b给出了复原行程具体的建模过程,图4c给出了从激励电流到滑片阀门节流面积的仿真模型。

图4 阻尼力仿真建模
基于某电动汽车后轮CDC减振器的结构参数设计如表1所示,仿真激励参数按表2进行设定。

表1 CDC减振器参数

表2 激励参数
3.2 仿真分析
图5给出了不同激励电流下该CDC减振器示功特性的仿真结果。结果表明,当激励电流增大时该CDC减振器的做功量是不断减小的。具体来说,当激励电流从0 A上升到1.6 A时,其复原行程最大阻尼力由4914 N下降到1331.8 N,可调范围增加了约72.9%;而其压缩行程最大阻尼力由1937.7 kN下降到1415.4 N,可调范围增加了约26.95%。
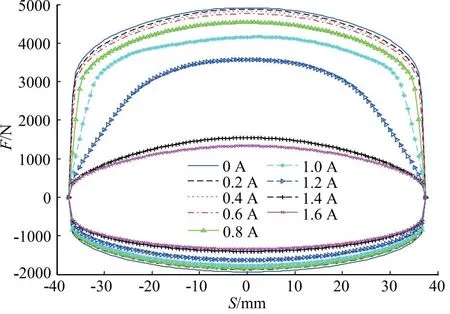
图5 示功特性仿真结果
进一步地,激励电流从0 A增加到0.4 A时,该减振器做功量的调节范围变化率较小,激励电流从0.4 A 增加到1.4 A时该减振器的调节范围变化率较大,从1.4 A切换到1.6 A时其调节范围变化率又变得缓慢下来。这是因为节流面积变化的速度随着激励电流的增加是先增大后减小的。
图6所示为不同激励电流下该CDC减振器阻尼力-速度特性曲线的仿真结果。结果表明,各激励电流下复原行程和压缩行程的特性曲线均由两段组成,阻尼力在“拐点速度”前呈现出明显的非线性关系,在“拐点速度”后基本呈现出线性关系。当激励电流增大时,其速度特性曲线的斜率在相应的减小,其 “拐点速度”也相应的变大,这是因为当相对运动速度小于“拐点速度”时,流经各个阻尼阀系的油量较少,其阻尼由各个阻尼阀系中的阻尼孔产生,而当相对运动速度大于“拐点速度”时,流经各个阀系的油量较大,其阻尼由各个阀系的阻尼孔、阀片形变后的溢流口及滑片阀门开口共同形成,当激励电流增大时,电磁阀的滑片阀门开口也相应的增大,致使“拐点速度”也变大。
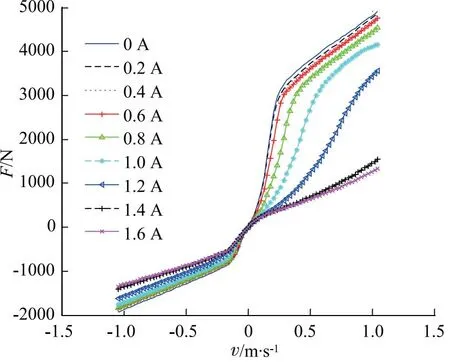
图6 速度特性仿真结果
3.3 实验分析
如图7所示为实验所获得该CDC减振器的示功特性曲线。结果显示,各个激励电流下的特性曲线较为饱和且完整,且与仿真结果的趋势基本吻合。其中,示功特性图中最大阻尼力在复原行程时略微向零点右侧偏移,而在压缩行程时略微向零点左侧偏移,这是因为台架中工装夹具存在惯性所导致。

图7 示功特性实验结果
如图8所示为实验所获得该CDC减振器的速度特性曲线。

图8 速度特性实验结果
表3和表4分别列出了不同激励电流时复原和压缩行程中最大速度下的阻尼力仿真值与试验值对比,整体上实验数据比较仿真数据大,这是因为仿真时未考虑实物样件存在摩擦力的情况,但两者相对误差均小于10%,可见仿真模型搭建正确可靠,可作为后续参数分析的基础。
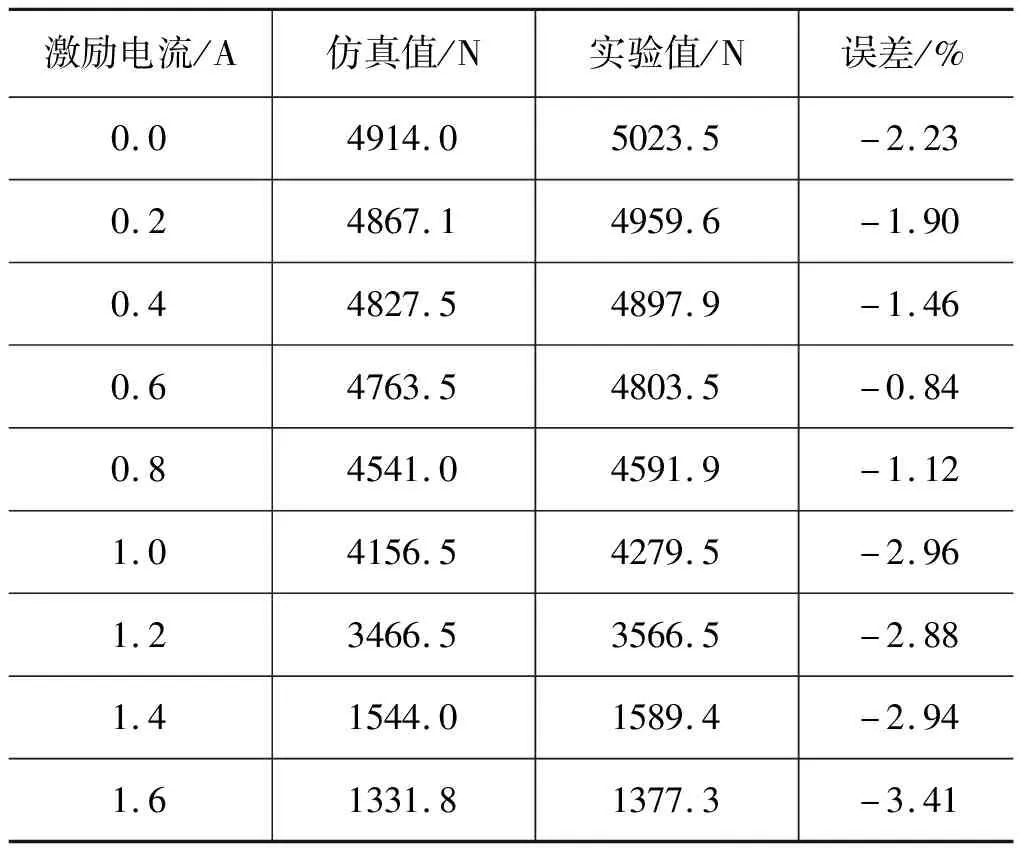
表3 复原行程最大阻尼力仿真与实验对比
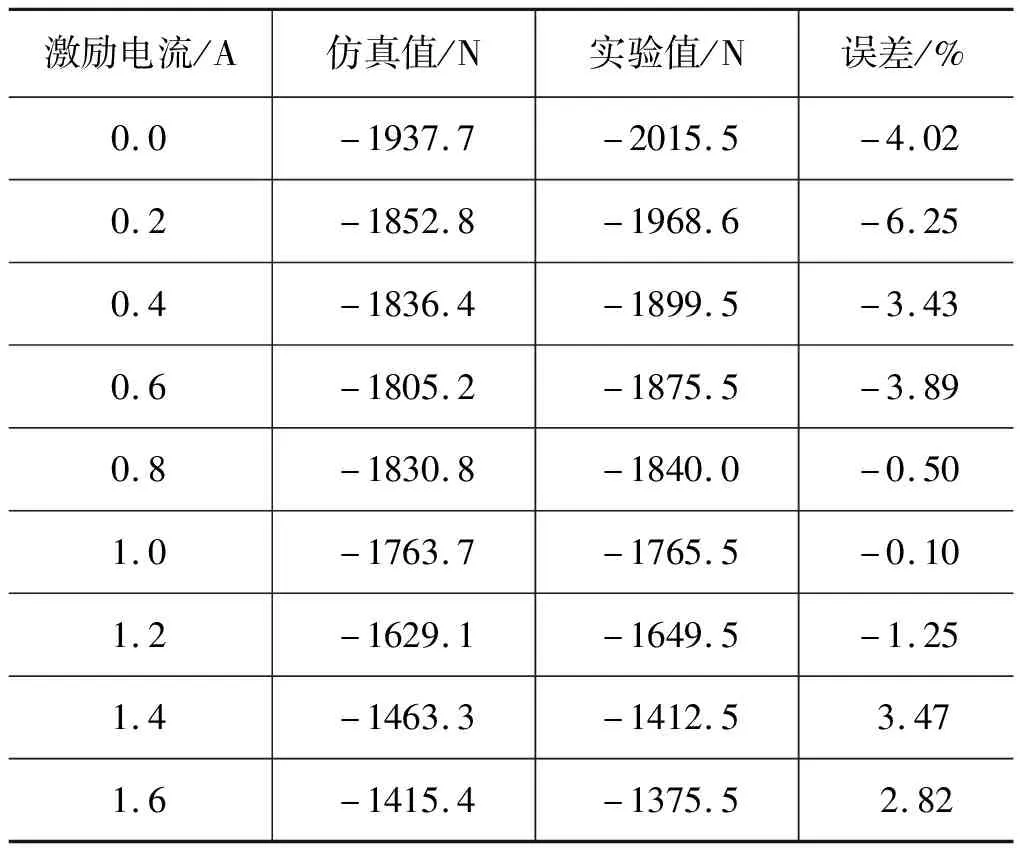
表4 压缩行程最大阻尼力仿真与实验对比
4 结论
(1) 设计了一种比例电磁阀内置式CDC减振器,基于流体力学搭建了其阻尼力模型,通过仿真和实验的方法获得了其阻尼特性曲线,对比显示仿真与实验相对误差小于10%,表明仿真模型准确有效;
(2) 该CDC减振器的阻尼力随着激励电流的增大而减小,且这种减小趋势的速率随着激励电流的增加先增加后减小;
(3) 速度特性曲线的斜率在“拐点速度”之前逐渐变大,在“拐点速度”之后基本不变,当激励电流增大时速度特性曲线的斜率在逐渐减小;
(4) 该CDC减振器的复原行程的阻尼力可调范围为1544~4914 N,压缩行程的阻尼力可调范围为-1415~-1937.7 N。可为其在后续整车上的调校提供理论依据。
