基于扩张状态观测器的海工栈桥液压系统模型预测控制
2024-04-25刘昊东李世振时文卓
刘昊东,李世振,时文卓
(山东大学 海洋研究院,山东 青岛 266237)
引言
随着海上风电行业的快速发展,对海上风电设备的维护需求也随之增长[1]。这就促进了海上换乘技术的发展,其中海工栈桥是用于运输维护人员和设备转移安全、高效的方式[2]。由于海洋环境的复杂多变,海上船舶在作业期间会受到风、浪耦合作用,进而不自主地产生平移和摇摆运动[3]。依靠船舶自身的动力定位系统可以在一定程度上削弱由海浪引起的艏摇、横荡和纵荡等运动,但无法有效控制船舶升沉、横摇以及纵摇方向上的运动[4]。
海工栈桥通过利用波浪补偿技术来抵消由于风、浪耦合作用而引起的船舶运动[5]。目前,海工栈桥所用的波浪补偿技术主要分为主动补偿和被动补偿[6]。其中被动补偿系统通常是由液压系统加装蓄能器来缓冲由波浪引起的船舶运动。被动补偿系统相当于一个弹簧阻尼器,可以实现被动地自我调节。被动补偿技术的优点是系统简单,装机功率低,成本较低。但是,被动波浪补偿技术有较大的延迟性补偿精度低,不适于在复杂海况下使用。主动补偿是通过传感器和控制系统来抵消由海浪引起的船舶运动[7]。为了监测船舶运动,海工栈桥通常采用一些运动检测单元,如惯性测量单元(IMU)和运动参考单元(MRU)。然后,根据所测船舶的姿态参数,控制系统操纵执行器做出相应的运动,使得栈桥末端与海上风机保持相对静止。用于海工栈桥主动补偿的执行器可以是液压马达或液压缸。主动式波浪补偿技术的优点是补偿精度高,能够快速响应并扩大作业范围,对恶劣海况的适应性更强。主动式波浪补偿技术的缺点是控制系统要求高,装机功率高,成本较高[8]。因此,主动补偿技术更适用于波浪补偿海工栈桥系统。海工栈桥作为一种大型海洋工程装备,通常以液压系统为主要驱动方式。目前,针对海工栈桥液压系统控制已有相关研究。JENSEN L M[9]针对海工栈桥液压系统控制提出了一种滞后补偿器来减少系统干扰。徐佳[5]针对海工栈桥的不同机构,提出了不同的液压系统控制策略。杜少彬[10]提出了一种基于船舶运动预报的动态面控制方法,有效提高了液压系统控制的实时性。张耘豪[11]考虑了执行机构的性能限制,提出了模型预测控制。
受海洋环境影响,海工栈桥会存在较大的外部扰动。同时,海工栈桥模型复杂,存在参数不确定、参数时变性强等特点,实际应用中难以建立海工栈桥的精确模型。由于无法得到精确的海工栈桥液压系统模型,因此传统的模型预测控制方法难以取得良好的控制效果。针对现有问题,本研究在模型预测控制基础上,引入扩张状态观测器(ESO),采用扩张状态观测器对液压系统外部负载扰动和机械系统未建模部分进行实时状态估计,并引入到模型预测控制器中,以提高海工栈桥液压系统的抗干扰能力。
1 系统描述
如图1所示为海工栈桥的整体结构,主要由回转机构、俯机机构以及伸缩机构组成。图中Lh为船舶甲板到俯仰关节之间的长度;Lt为伸缩机构第二节梯架的长度;θ1为回转机构的关节角度;θ2为俯仰机构的关节角度;dt为伸缩机构的关节角度。
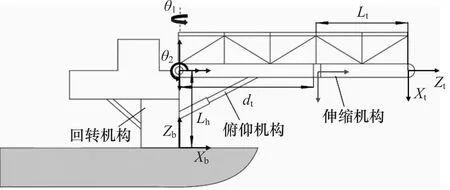
图1 海工栈桥结构图
回转机构的执行器为液压马达,而俯仰和伸缩机构的执行器为液压缸。为了便于研究,假设海工栈桥各部分均是刚性连接,且质量分布均匀[12]。同时其中,俯仰机构所补偿的升沉运动最为复杂,且海工栈桥各执行机构均为三阶系统[13]。因此,本研究针对俯仰机构的液压系统进行相关控制研究。
1.1 运动学分析
根据D-H法建立如图1所示的参考坐标系,通过对逆运动学进行求解,可以得到海工栈桥末端位移到俯仰机构位移的运动学关系:
(1)
式中,X,Z为海工栈桥末端位置坐标。
图2为俯仰机构与其液压系统的运动关系图。其中,y为液压杆伸缩位移,α与俯仰机构角位移有关,l1,l2为俯仰机构连杆长度。
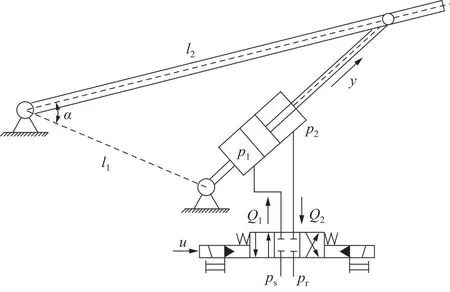
图2 俯仰机构液压系统运动学
由此可得,海工栈桥俯仰机构运动与液压系统的运动学关系为:
(2)
(3)
1.2 液压系统动力学模型
根据牛顿第二定律,可得海工栈桥液压系统的动力学方程为:
(4)
式中,m——俯仰机构质量
y——液压缸位移
p1,p2——液压缸左右两腔油压
A1,A2——液压缸左右两腔的有效活塞面积
B——有效黏性阻尼系数
d——液压系统外部负载扰动以及机械系统未建模部分
液压缸两腔压力动态方程为:
(5)
式中,βe1,βe2——液压缸左、右两腔液压油弹性模量
V01,V02——液压缸左、右两腔初始容积
Q1,Q2——液压缸进油流量和回油流量
液压伺服阀流量方程为:
(6)
其中:
(7)
式中,kq——伺服阀阀芯位移流量增益
ki——伺服阀阀芯位移比例增益
ps——海工栈桥液压系统的供油压力
pr——海工栈桥液压系统的回油压力
定义符号函数:
(8)
(9)
式中,f(x)=[f1f2f3]T,
g(x)=[0 0gc]T,
G=[0 -k0],d(t)=sin(4πt)。
2 控制器设计
针对海工栈桥液压系统的外部负载扰动以及机械系统未建模部分,利用扩张状态观测器对其进行实时估计[14],并引入模型预测控制器中进行补偿。首先,将海工栈桥液压系统模型进行线性化、离散化处理,进而得到系统的预测方程。其次,引入扩张状态观测器对系统状态和扰动进行实时估计以此抵消扰动对系统的影响。最后,定义目标函数和约束条件,对QB问题进行求解。海工栈桥液压系统控制框图如图3所示。

图3 栈桥液压系统控制框图
2.1 模型预测控制器设计
非线性模型预测控制是以非线性模型作为预测方程,这会导致控制系统较大的计算负担[15],同时系统的响应时间增加,存在较大延时。相比之下,线性时变模型预测控制的预测模型为线性时变模型,计算较为简单并且有较好的实时性。由于受复杂海洋环境的影响,海工栈桥所受到的波浪影响变化较快,需要液压系统能够及时作出响应,对实时性要求较高,因此本研究所用的模型预测为线性时变模型预测控制。
首先,对海工栈桥液压系统进行线性化处理。对式(9)在参考轨迹点采用泰勒级数展开,同时忽略高阶项,仅保留一阶项:
(u-ud)
(10)
式中,xd——参考轨迹点的状态向量
ud——参考轨迹点的控制向量
进而得到液压系统的线性模型为:
(11)
模型预测控制多用于数字控制系统[16],因而需要进一步对海工栈桥液压系统模型进行离散化处理。取采样时间为T,并使用一阶差分进行离散化,得到离散的状态空间方程:
(12)

根据式(12),以初始值为最新状态值,设定预测时域为Np,控制时域为Nc且Np≥Nc,同时定义:
(13)
由此可得海工栈桥液压系统的预测方程为:
yp(k+1|k)=ΨxΔx(k)+ΨτΔu(k)+Υd(k)
(14)
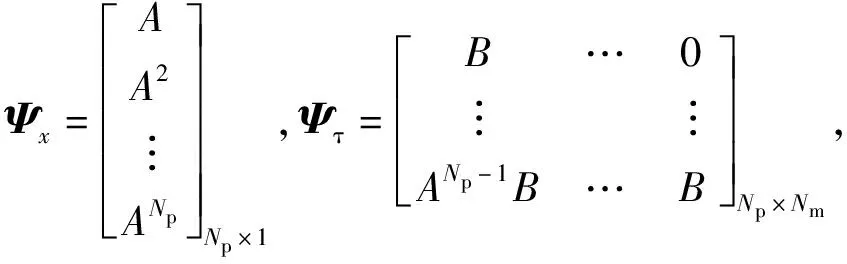
为了使海工栈桥液压系统跟踪指定的参考轨迹,定义成本函数为:
(15)
式中,Δu(k+i)——k+i时刻的控制输入增量
y(k+i|k)——控制输出预测值
yref(k+i|k)——控制输出参考值
(k+i|k)——在k时刻预测k+i时刻的系统信息
R——控制误差的权重矩阵
S——控制输出的权重矩阵
ρε2——松弛因子,防止过程中出现没有可行解的情况
下一步将成本函数转化成二次规划形式,将预测方程式(14)代入目标函数式(15)中:
Ep(k+1|k)=Xd(k+1)-ΨxΔx(k)-Υ(k)
(16)
定义海工栈桥的状态和输出约束条件为:
(17)
式中,Xmin,Xmax——液压系统状态阈值
umin,umax——液压系统控制输入阈值
通过二次型求解方法,求出液压系统在控制时域内的一系列控制增量:
ΔU*=[Δu*(k),Δu*(k+1),…,Δu*(Nc-1)]T
(18)
将控制序列的第一个元素Δu*(k)作为实际的控制输入增量作用于系统,即
u(k)=u(k-1)+Δu*(k)
(19)
在下一采样时刻(k+1时刻),系统根据新的状态值x(k+1)返回式(13)重新进行优化求解,如此循环实现海工栈桥液压系统的整个控制过程。
2.2 扩张状态观测器设计
在复杂的海洋环境中,受风、浪耦合影响以及内部未知动态导致的海工栈桥系统扰动是实时存在的。扰动的存在会严重影响控制器的稳定性以及控制精度,导致控制性能降低。为了有效降低扰动对控制器的影响,本研究采用自抗扰控制中的扩张状态观测器来实现对扰动的实时估计,并将其引入到模型预测控制器中进行补偿,以此提高模型预测控制的鲁棒性。
扩张状态观测器是通过将系统的外部扰动以及系统未建模部分统一合并为“总扰动”[17],将总扰动扩张成一个新的状态量,利用系统的输入输出来观测系统所有的状态量以及扩张出来的总扰动。

(20)
式中,h(t)为有界的不确定函数。
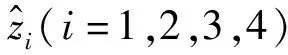
(21)

qi——观测器参数且为qi>0
采用“带宽法”[18],取观测器的带宽为ϖ0,则有如下关系式:
s4+q1s3+q2s2+q3s+q4=(s+ϖ0)4
(22)
3 结果与分析
Marine Systems Simulato (MSS)是一个用于海洋控制系统设计的仿真工具箱,可以在MATLAB/Simulink平台上运行,支持多种海洋系统的数学建模和仿真[19]。本研究使用 MSS工具箱,来获得由海浪引起的船舶升沉运动。海浪模型采用JONSWAP海浪谱,有效波高2.5 m,峰值频率0.68,对应4级海况。所用船舶为长度82.2 m,排水量6362 t的供应船。所得的船舶升沉运动位移h如图4所示。

表1 海工栈桥液压系统参数
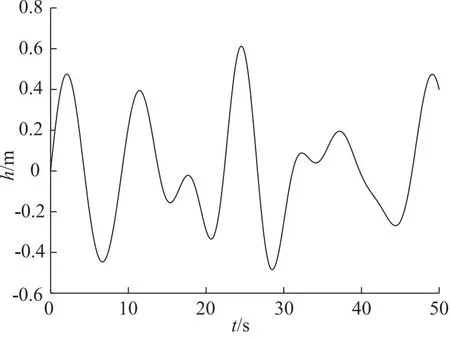
图4 船舶升沉运动
为验证所设计控制器的性能,在Simulink仿真中搭建仿真模型。为了便于突出基于扩张状态观测器的模型预测控制性能优势,模型预测控制器参数取值相同。模型预测控制器相关参数:预测时域Np=10,控制时域Nc=5,采样时间T=0.1 ms,控制误差权重R=2e12,控制输出权重S=800,松弛因子ρε2=1000;扩张状态观测器相关参数:ϖ0=1000;系统扰动增益为k=3000。
图5为海工栈桥液压系统补偿位移y跟踪情况。图6为海工栈桥液压系统补偿位移跟踪误差e。经过对比发现,与传统的模型预测控制相比,基于扩张状态观测器的模型预测控制其控制精度得到显著提高,具有良好的补偿效果。
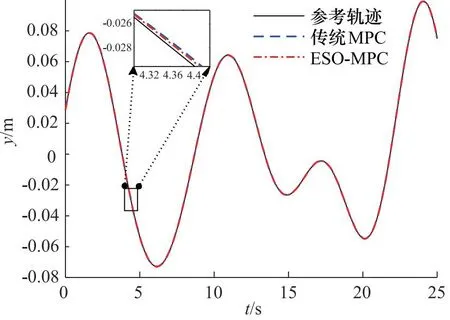
图5 补偿位移跟踪效果
图6 补偿位移跟踪误差
图7为扩张状态观测器对液压系统速度z2的估计。图8为扩张状态观测器对液压缸左右两腔压力差z3的估计。图9为扩张状态观测器对液压系统总扰动z4的估计。仿真结果表明,扩张状态观测器对液压系统状态具有良好的观测性能。同时,对液压系统的扰动具有良好的估计效果,能够实时估计出扰动值。
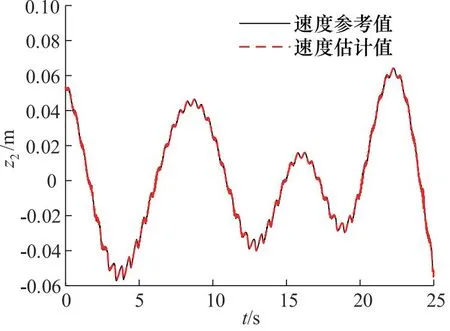
图7 速度估计
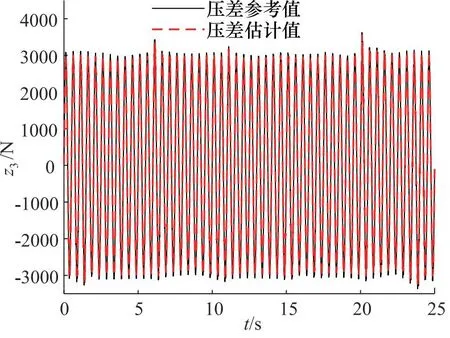
图8 压力差估计
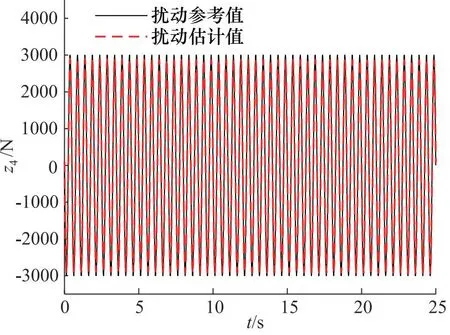
图9 扰动估计
为评估控制器性能,引入以下指标:误差绝对值的最大值Emax、平均值Emean以及标准差Estd。
误差绝对值的最大值:
(23)
误差绝对值的平均值:
(24)
误差绝对值的标准差:
(25)
控制器各性能指标如表2所示。误差绝对值的最大值反映了控制系统在整个控制过程中误差的最大幅度,基于扩张状态观测器的模型预测控制与传统模型预测控制相比具有良好的抗干扰能力。误差绝对值的平均值反应了误差的平均水平,可见基于扩张状态观测器的模型预测控制精度较高。误差的标准差反映了控制系统误差相对平均值的变化程度,基于扩张状态观测器的模型预测控制的标准差较小,表现出更好的稳定性。
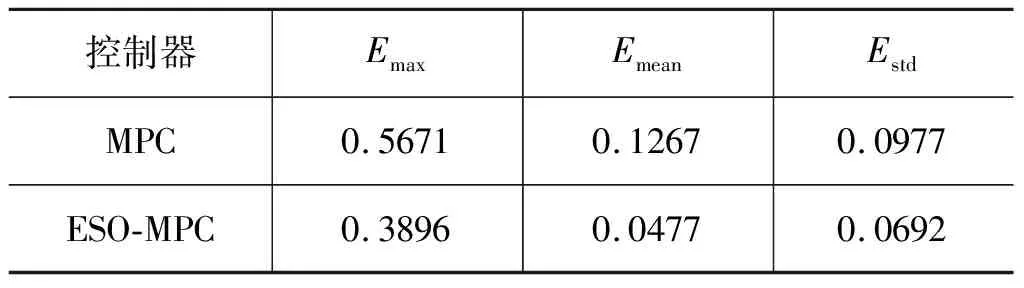
表2 控制器性能指标
4 结论
本研究设计了一种基于扩张状态观测器的海工栈桥液压系统模型预测控制器,在模型预测控制的基础上引入扩张状态观测器,以此来抵消海工栈桥液压系统外部负载扰动以及机械系统未建模部分对控制器性能造成的影响。通过对仿真结果进行分析,可以得出以下结论:
(1) 扩张状态观测器对系统状态和扰动具有良好的观测能力,有效提高了模型预测控制的波浪补偿效果。
(2) 与传统的模型预测控制相比,其鲁棒性和稳定性都有很大提升,控制效果良好。
