2D-C/SiC 复合材料热膨胀系数演化模型

2024-04-25郑茹悦杨成鹏贾斐

复合材料学报 2024年4期

郑茹悦, 杨成鹏*, 贾斐

( 1.西北工业大学力学与土木建筑学院，西安 710072；2.西安电子科技大学机电工程学院，西安 710071 )

陶瓷基复合材料具有高比强、高比模、可设计性好、耐腐蚀等突出的力学性能，因此在航空、航天等领域得到广泛应用，如飞行器尾椎管、发动机喷管和延伸段、卫星支架及火箭整流罩等[1-4]。然而，陶瓷基复合材料在实际应用中往往会处于超高温状态，并且存在一定的高温突变，服役条件极为恶劣，这就要求其具有较高的热稳定性。

热膨胀系数(TEC) 是表征复合材料热稳定性的重要参数，也是进行材料设计的关键参数。近年来基于数值方法预测复合材料单向板或层合板理想状态宏观TEC 的研究逐渐成熟[5-9]，而对于复合材料TEC 的理论预测，国内外也有许多学者从不同角度作了相关研究。Tuner[10]假定复合材料中存在均匀应力，且各组分随温度的变形是受限膨胀，基于应力平衡理论最早提出了复合材料线膨胀系数的经验方程；Chamberlain 等[11]基于平面厚壁圆筒解答推导了单向复合材料纵向和横向TEC 的表达式；Schapery[12]依据热弹性极值原理提出了一种求解各向同性和各向异性复合材料TEC 上下限的方法，并给出弹性和粘弹性复合材料的体积膨胀系数和线膨胀系数的解析公式；宋美慧等[13]考虑纤维不同方向热变形能力的差异对复合材料横向TEC 的Schapery 公式进行了修正，并建立层合复合材料二维平面内TEC 的计算模型；刘兵山等[14]从构成层合板的组分材料出发，根据弹性力学方法和理想界面的均匀化方法，得到以单层TEC 表示的对称层合板的宏观等效TEC 表达式，其中纤维的热性能为横观各向同性，基体为各向同性。然而，对于含损伤纤维增强复合材料TEC 的研究较少，且大多采用有限元模型预测[15-17]。梁军等[18]运用Mori-Tanaka 方法预测了含随机分布微裂纹的纤维增强复合材料的宏观TEC；何乾强等[19]采用细观力学方法，建立了纤维增强复合材料包含基体微裂纹和纤维/基体界面脱粘的热胀/冷缩理论模型。

材料的宏观TEC 不仅取决于各组分的热膨胀性能，还受到材料的力学参数、热失配应力、结构形式等因素的影响[20-21]。李开元等[22]通过试验研究了不同纤维编织结构C/SiC 复合材料的轴向热膨胀行为；邱雪琼等[23]以T800 级碳纤维增强复合材料为研究对象，测试了不同铺层复合材料层压板的面内热膨胀系数，研究了铺层对热膨胀系数的影响规律；Zhang 等[24]通过试验研究了1D、2D 和3D-C/SiC 复合材料的轴向TEC 随温度的演变行为；Sun 等[25]全面总结论述了单向复合材料、层合复合材料、编织复合材料TEC 的理论预测模型、有限元计算模型及实验研究进展，并提出了考虑孔隙率和纤维体积分数的数值仿真方法。由于陶瓷基复合材料在受载时通常产生基体开裂、界面脱粘滑移和纤维桥连等损伤模式[26]，在TEC预测模型中考虑这些损伤因素是必要的。然而，这方面的研究不够，目前尚缺乏同时考虑多种影响因素的温度相关TEC 演变模型。

本文以2D-C/SiC 复合材料为研究对象，首先基于同心圆柱单胞模型，考虑纤维轴向和径向力学性能的差异以及泊松效应的影响，给出任意温度下的热失配应力计算模型；在此基础上分析基体开裂、界面脱粘等损伤对Mini 复合材料热膨胀变形的影响，推导材料轴向和径向的TEC 计算模型。最后基于正交层合板模型，考虑热残余应力的影响，建立2D-C/SiC 复合材料的表观TEC 预测模型，并结合试验数据进行分析论证。

1 束内热失配应力

对于平纹编织结构，纵向纤维束和横向纤维束的热膨胀不匹配会导致束间产生热失配应力；而对于纵向或横向纤维束而言，纤维和基体热膨胀系数的不同也会在束内产生一定的热失配应力[27]。在C/SiC 体系中，基体的热膨胀系数远大于纤维轴向热膨胀系数，因此从制备温度冷却后，轴向上基体受拉而纤维受压[28]。不同温度下复合材料的内应力场不断演化，且室温时的热残余应力值较大；热残余应力随温度的升高而逐渐释放，在达到制备温度时热失配应力几乎降为0。

在计算束内热残余应力时，由于2D-C/SiC 复合材料的纤维长径比很大，因此可采用图1 所示的同心圆柱单胞模型，其中，纤维和基体半径分别用rf和rm表示。

图1 同心圆柱单胞模型Fig.1 Concentric cylindrical unit cell model

由束内热失配而导致的纤维和基体轴向、径向及环向热残余应力分量可分别表示为[29]

式(1)中各参数A～F定义如下：

式中：E1f和ν1f分别表示纤维材料的轴向弹性模量和泊松比；E2f和ν2f分别表示纤维的径向模量和泊松比；Em和νm是基体的弹性模量和泊松比；α1f和α2f分别为纤维的轴向和径向热膨胀应变；αm是基体的热膨胀应变；T表示任意温度；Tp为制备温度。

2 Mini 复合材料热膨胀变形分析

从定义上讲，热膨胀指的是物体长度或体积随温度升高而增大的现象，而热膨胀系数指的是物体在热胀冷缩效应下，其几何特性随温度变化的规律性系数。热膨胀系数分为线膨胀系数α和体膨胀系数β，前者表示物体在单位温度变化下，某一方向上长度的相对变化率，后者则表示体积的相对变化率。对于Mini 复合材料，可用长度的变化程度近似衡量其纵向和径向的线膨胀系数。

热膨胀系数在实际测量中通常以室温T0为零变形参考点，设该温度下模型原长为l0，温度升高至T后长度的增加量为Δl，根据热膨胀系数的物理含义，则任意温度T下的热膨胀系数为[30]

其中，ε为平均热膨胀应变。因此，求解热膨胀系数的关键，是确定材料的平均热应变。

2.1 纵向变形分析

2D-C/SiC 材料从制备温度Tp冷却至室温T0的过程中会产生较大的热失配应力，从而导致基体发生开裂现象，界面层和纤维之间发生脱粘[31]。设初始裂纹间距为L，选取长度为L/2 的Mini 复合材料单胞，其包含单根纤维及周围基体，如图2所示，则在裂纹面上，纤维和基体的应力均为0。

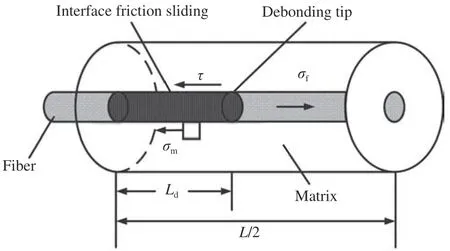
图2 Mini 复合材料细观损伤模型Fig.2 Microscopic damages model of minicomposite

图中，纤维和基体的应力分别用σf和σm表示，界面滑移应力用τ表示，Ld表示界面脱粘长度，由下式给出[32]：

其中，σth(T0)表示圆柱体模型在T0时刻的纵向热失配应力，其表达式为

由于单胞在纵向上不受外力，因此必须满足应力平衡方程σfVfb+σmVmb=0。假设剪切应力只在基体中传递，而基体通过界面将剪切应力传递到纤维中，可设剪应力τ为常数，根据剪力滞后原理[33]给出纤维的平衡微分方程为

需要注意的是，在进行圆柱体模型变形分析时，应用到的热应力分量均为式(1) 所示的束内热应力。

2.1.1 室温下的纵向变形

在室温T0下纤维和基体的应力分布情况由图3 中的实线部分所示。

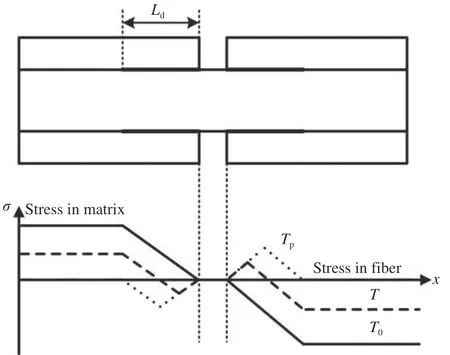
图3 纤维和基体的应力分布Fig.3 Stress distribution of fiber and matrix

根据剪滞原理以及平衡方程得到在室温下纤维和基体在脱粘段内的轴向应力分布表达式为

在脱粘段外纤维和基体仍保持初始残余应力的水平，即

以制备温度Tp作为参考点，假设该温度下纤维和基体均处于无应力状态，见图4。当温度降至室温T0时，材料内部会出现基体开裂和界面脱粘现象，并伴随有热失配应力的产生。

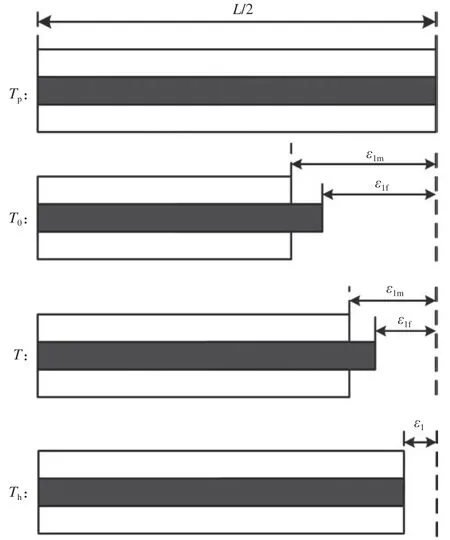
图4 纵向热膨胀变形图Fig.4 Deformation diagram of longitudinal thermal expansion

从制备温度Tp到室温T0，纤维在脱粘长度范围内由于应力作用产生的轴向收缩应变为

而基体在脱粘长度范围内由于应力作用产生的轴向收缩应变为

在脱粘段外(Ld,L/2)，与热残余应力相对应的纤维轴向收缩应变为

而基体的轴向收缩应变为

在整个模型范围内，纤维和基体与应力相对应的收缩应变由式(11)～(14)给出，并应在长度方向进行均匀化处理；除此之外，从制备温度Tp降至室温T0，材料还会产生冷却收缩应变。因此，室温时纤维和基体的总收缩应变可分别表示为

2.1.2 高温下的纵向变形

单胞受热膨胀后，裂纹面附近的纤维/基体界面上出现正向滑移区和反向滑移区，它们的相对滑移方向相反，如图5 所示[34]。设反向滑移区长度为L1；并用I、II、III 段分别表示反向滑移区、正向滑移区和界面完好区。纤维和基体的应力分布情况如图3 中虚线所示，其中分别给出了制备温度Tp和任意温度T下的应力分布曲线。此时，界面仍可分为脱粘段和完好段两部分，模型的变形计算方法与室温下类似，只是脱粘部分需将正向滑移区的变形与反向滑移区的变形叠加起来。

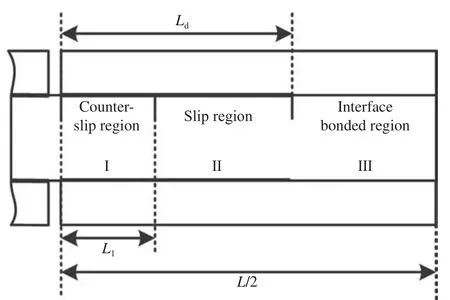
图5 基体相对纤维滑移示意图Fig.5 Schematic of matrix sliding relative to fiber

下面先计算脱粘段的轴向变形。

在反向滑移区(0,L1)内，纤维和基体的轴向应力分布为

式(16)对应的纤维和基体轴向收缩应变分别为

在正向滑移区域(L1,Ld)内，应力分布曲线的斜率与反向滑移区绝对值相等，符号相反，由下式表示：

式(18)对应的纤维和基体轴向收缩应变分别为

事实上，在升温过程中，界面滑移区的分布也会有所变化，根据应力连续条件，反向滑移长度为

由于纤维应变在I 段和II 段的表达式不同，应进行平均化处理。结合式(17)和式(19)，在脱粘段(0,Ld)内，与热失配应力相对应的纤维收缩应变可表示为

同理，基体收缩应变可表示为

显而易见，式(21)和式(22)是温度相关的函数，说明在升温过程中，每一时刻材料内部的变形并不一致。

在脱粘段外(Ld,L/2)，即第III 段界面结合完好区域，纤维和基体除了受到轴向热失配应力的影响外，还各自承受径向和环向热失配应力。根据弹性体的胡克定律，该区域内纤维和基体的轴向收缩应变分别为

当脱粘段内纤维与基体的轴向热膨胀应变相等时，基体裂纹将闭合，该现象对应的数学表达式为

通过式(24)可求解出基体裂纹愈合温度Th。

基体裂纹愈合前后Mini 复合材料的热膨胀机制并不相同。裂纹愈合前，基体的轴向热膨胀变形需要填充裂隙，其对模型整体的轴向热膨胀变形贡献减少；裂纹闭合后，纤维与基体在轴向的热膨胀变形将协调一致。

考虑组分材料的自由热膨胀变形，在纵向上对模型整个长度范围内的应变进行平均即可得到裂纹闭合前(T≤Th)纤维和基体在半裂纹间距内的总轴向应变，分别为

当基体裂纹闭合后(T≥Th)，纤维和基体的应变应满足ε1f(T)=ε1m(T)，且有

综上，相较于T0状态，组分材料在温度T下产生的总的热膨胀应变为

由于基体在升温过程中需要填充裂纹缝隙，因此，在裂纹闭合前圆柱体模型总的轴向膨胀应变应该用纤维变形量表示，即

当温度升至Th，基体裂纹闭合，此时纤维和基体的轴向热膨胀变形满足协调条件，有

将式(28)和式(29)分别代入TEC 的定义式(4)，即可得Mini 复合材料的纵向损伤热膨胀系数α1。

2.2 径向变形分析

假设圆柱体模型从T0至T0+ΔT的温度变化过程是均匀的，那么纤维和基体的径向应变函数ε2f和ε2m只与半径和温度有关[35]。

2.2.1 室温下的径向变形

由于2D-C/SiC 组分材料热膨胀系数的差异，从制备温度Tp冷却至室温T0，纤维和基体内部均会产生较大的径向残余拉应力。上述拉应力会导致纤维发生径向扩张，而基体向内收缩。与轴向变形分析相同，假设在脱粘段内模型不受径向和环向应力的限制，那么在室温T0下，纤维和基体在脱粘长度范围内由于应力作用而产生的径向收缩应变分别为

完好段纤维和基体由于应力作用产生的径向收缩应变分别为

在径向，纤维和基体变形相对独立，那么由应力作用而引起的总收缩变形应该是各组分收缩位移之和，如图6 所示。同时，从制备温度Tp到室温T0，纤维和基体还会有额外的径向冷却自由收缩应变产生。因此，室温时脱粘段内模型的径向收缩应变为

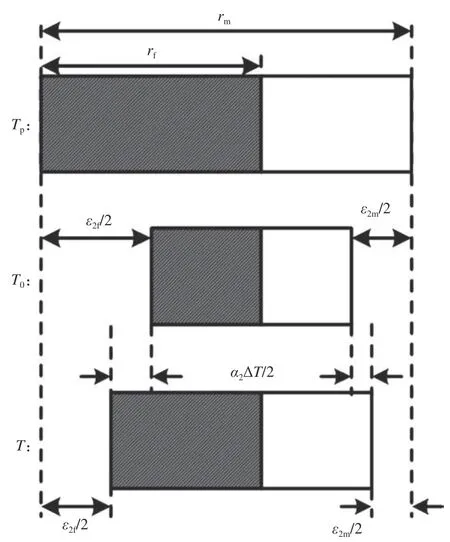
图6 径向热膨胀变形图Fig.6 Deformation diagram of radial thermal expansion

脱粘段外，即模型第III 段的径向收缩应变为

对于宏观整体Mini 复合材料，其径向热收缩应变取裂纹间距范围内的变形平均值，即

以此保证材料径向变形在宏观层面协调一致。

2.2.2 高温下的径向变形

与纵向同理，纤维和基体受热膨胀后，其径向变形均由两部分组成，一是与热失配应力相对应的变形，二是自由热膨胀变形。由于第一部分变形包括径向热失配应力和泊松效应导致的变形，因此纤维和基体的径向收缩应变分别为

而在脱粘长度外，由热失配应力引起的纤维径向收缩应变为

基体径向收缩应变为

模型在界面脱粘段I-II 内的径向收缩应变可以由纤维和基体的变形之和得到，即

而界面完好区，即第III 区域内的径向收缩应变为

对I-II 区域和III 区域的应变在裂纹间距范围内取平均值即可得到任意温度T下的径向热收缩应变，即

以室温为参照，Mini 复合材料在温度T下产生的总的径向热膨胀应变为

将式(41) 代入TEC 的定义式(4)，即可得Mini 复合材料的径向损伤热膨胀系数α2。

2.3 表观热膨胀变形分析

对于2D-C/SiC 复合材料，其纵向和横向纤维束的数量与形状均相同，可视为[0/90]正交铺设对称层合板[36]，且各单层的纤维是单向平行的，如图7 所示。将纤维方向记为L 方向，也称纵向；垂直纤维方向记为T 方向，也称横向。

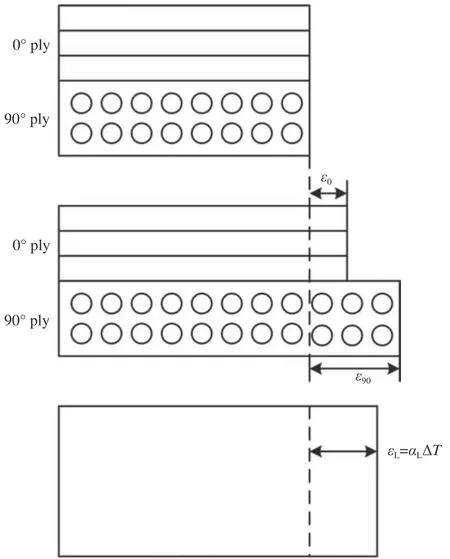
图7 [0/90]层合板膨胀变形图Fig.7 Expansion deformation diagram of [0/90] laminate

当温度升高ΔT(ΔT=T-T0)时，0°层和90°层的应变值分别用ε0和ε90表示，两个方向变形相互协调使整体层合板产生一个纵向应变εL。设整体层合板模型的轴向损伤膨胀系数为αL，则当温度升高ΔT时应变量可表示为αLΔT，变形关系见图7。

根据上文已经求得单层的纵向和横向损伤膨胀系数α1和α2，那么对于[0/90]正交层合板，在基体裂纹愈合前，从制备温度Tp冷却至任意温度T，0°层热自由应变Ω1(T)和90°层热自由应变Ω2(T)为

基体裂纹愈合后，以愈合温度Th为参照，0°层热自由应变Ω1(T)和90°层热自由应变Ω2(T)为

在无损伤情况下，0°层和90°层的模量可用下式表示：

其中，Vf和Vm分别为整体复合材料中纤维和基体的体积分数。损伤后，0°层的纵向模量可近似表示为[37]

其中，参数η=Ld/L定义为界面脱粘率，用于表征界面的损伤程度，η取0.5 表明界面完全脱粘。而90°层损伤模量可估算为

对于单层而言，其纵向与横向的热膨胀系数并不相同，因此在层间也会产生一定的热失配应力。从制备温度Tp冷却至任意温度T，对0°层和90°层而言与层间热失配应力相对应的应变可分别表示为

其中，ν1f和νm分别为纤维和基体的泊松比。

单层的纵向和横向热失配应力应满足平衡方程：

其中，tL和tT分别表示0°层和90°层的厚度，且在平纹编织单层中，有tL=tT，因此和应满足：

结合式(42)、式(43)和式(47)可得任意温度T时0°层和90°层沿纵向的应变分别为

在热失配应力的作用下，0°层和90°层的变形将协调一致，即0°层和90°层满足等应变假设，有

联立式(50)～(52)，可得2D-C/SiC 复合材料的表观应变εL为

从室温T0升至任意温度T，材料的热膨胀应变可表示为

将式(54)代入TEC 的定义式(4)，即可得层合板模型的平均热膨胀系数αL。

3 经典热膨胀系数计算模型

Schapery[12]根据能量理论推导出了单向纤维增强复合材料的热膨胀系数α1和α2，其中纤维和基体均被假定为各向同性材料，然而后续研究发现，纤维在不同方向上的强度及刚度具有差异性，因此计算时应予以考虑。基于纤维的横观各向同性性质，宋美慧等[13]将Schapery 模型的α2进行改进，得到修正Schapery 模型，即

式中：Ω1f(T)、Ω2f(T) 和Ωm(T)分别代表纤维轴向和径向以及基体的热膨胀应变；Ω1(T)表示单向板的纵向热膨胀应变，且有Ωi(T)=αi(T)-αi(T0)。

4 模型应用与讨论

4.1 试验验证

试验用2D-C/SiC 复合材料由西北工业大学超高温结构复合材料重点实验室采用化学气相渗透工艺制备而成，组分材料为T300 碳纤维(纤维丝束数为3 K)、热解碳界面和SiC 基体。复合材料平板的纤维体积分数为40vol%，单层为平纹编织结构，单层厚度为0.2 mm，经过裁剪得到尺寸为3 mm×4.5 mm×25 mm 的热膨胀测试样件。由于热膨胀系数测试值的分散性小，因此仅采用两个试件T1 和T2，试件来自两个生产批次，密度分别为2.1 g/cm3和1.8 g/cm3。

采用德国耐驰NETZSCH 公司生产的DIL 402SE 热膨胀仪，对不同温度下2D-C/SiC 复合材料的热膨胀系数进行测定。测试过程中以氩气作为保护气体，测量温度范围为室温至1 400℃，升温速率为5℃/min。

两个试件的测试数据如图8 所示，可以看出，在室温到1 473 K 范围内，2D-C/SiC 复合材料的表观TEC 随温度的升高而持续增大，当温度大于1 473 K 之后，表观TEC 趋于稳定。此外，两个试件的热膨胀系数具有明显差别，试件T2 的热膨胀系数整体上低于T1 试件，但两个试件热膨胀系数随温度的演变规律相同。基于该实验数据，以下将对本文模型的合理性进行验证，并通过参数分析阐明两个试件测量结果的差异性。

图8 2D-C/SiC 复合材料表观热膨胀系数(TEC)的试验曲线及预测值Fig.8 Tested and predicted curves of apparent thermal expansion coefficient (TEC) of 2D-C/SiC composites

Munro[38]给出了0～1 500℃范围内α-SiC 的累计热膨胀应变，这里将表达式变更为

以满足300～1 773 K 温度范围内的适用性。

Pradere 等[39]测定了聚丙烯腈(PAN)基碳纤维的轴向热膨胀应变α1f和径向热膨胀应变α2f随温度的变化规律，即

式(57)在300～1 800 K 温度范围内适用。

2D-C/SiC 复合材料各组分材料的其他材料参数及参数值如表1 所示。

表1 2D-C/SiC 复合材料模型基本参数Table 1 Basic parameters of 2D-C/SiC composites model

根据表1 的材料参数值，计算出Mimi 复合材料的纵向损伤TEC 随温度的变化规律如图9(a)所示。可以看出，在室温到1 673 K 的范围内，纵向TEC 随温度的升高而持续增大。通过式(24)求得的裂纹愈合温度为Th=1 585 K，裂纹愈合后，基体膨胀不再填充裂隙，因此Mini 复合材料纵向TEC 曲线呈轻微上扬趋势。图9(b) 给出了Mimi 复合材料的径向损伤TEC 随温度的变化规律，可以看出，α2的变化规律与α1相似，但α2的值显著高于α1。

图9 Mini 复合材料纵向(a)和径向(b)TEC 预测曲线Fig.9 Predicted curves of longitudinal (a) and radial (b) TEC of minicomposites

图9(a)和图9(b)中同时给出了本文模型不考虑损伤时(界面脱粘长度Ld=0)的预测值，以及修正Schapery 模型的预测值。可以看出，本文模型在不考虑损伤时的预测值略高，表明损伤降低了材料的热膨胀变形。与本文模型相比，修正Schapery 模型对Mini 复合材料TEC 的预测曲线略高，这可能是由于本文模型考虑了两个尺度的热失配应力对热膨胀变形的限制作用，其一是细观尺度的纤维和基体内应力，其二是介观尺度的层间内应力，这些应力的协同影响共同导致本文模型给出了略低的纵向和横向热膨胀系数。另外，Schapery 模型仅考虑了纤维和基体的纵向热残余应力，忽略了基体裂纹和界面脱粘等损伤对热膨胀变形的影响。然而，研究表明：组分材料沿纤维环向和径向上也存在较大的热失配应力，且初始损伤对热膨胀同样具有一定的影响。

根据α1和α2的预测值，结合正交层合板模型，可计算出2D-C/SiC 复合材料的轴向热膨胀系数随温度的变化规律，如图8 所示。对比发现：(1) 模型预测曲线与试件T1 的测试值均吻合较好，在温度较低时理论值偏高，这是由于热膨胀变形的初始阶段受内部孔隙率的影响较大，裂隙填充抵消了部分膨胀变形；(2) 本文模型在不考虑损伤的情况下给出了略高的表观TEC 预测值，说明基体开裂和界面脱粘的引入使材料的热膨胀变形减小，但总体上曲线的趋势并没有由于损伤而发生改变；(3) 同等参数条件下，修正Schapery 模型给出了偏高的材料表观TEC 预测值。

总体上，模型预测值与试验值具有基本相同的变化趋势，吻合度较高，这证明了本文模型的合理性。然而在初始段及末尾段附近，模型与试验曲线在变化趋势上存在一定差异，分析其原因可能主要有以下3 方面：(1) 纤维和基体的热膨胀系数都会随温度而变化，但由于缺乏纤维和基体的就位热膨胀性能实验值，由此可能会给计算结果带来一定误差；(2) 2D-C/SiC 复合材料的内部孔隙率可能达到15%甚至20%，因此其初始阶段的热膨胀变形增长速率可能达不到理论值，试验测试值偏低；(3) 在径向，纤维和基体间可能存在界面裂隙，在界面裂隙愈合前，纤维和基体的径向膨胀变形将填充裂隙空间，因此初始阶段表观TEC 的理论增长速率值可能偏大。

复合材料热膨胀系数的影响因素众多，下面分别讨论纤维径向模量、基体模量和孔隙率、损伤参数及基体膨胀系数对复合材料热膨胀系数的影响。

4.2 参数分析

4.2.1 纤维径向模量的影响

当环境温度为1 000 K 时，计算出纤维径向模量对Mini 复合材料纵向及横向TEC 的影响规律，如图10(a) 所示，其中τ=10 MPa，L=400 µm。可以看出，当其他参数一定时，纤维径向模量越大，Mini 复合材料的纵向TEC (α1)越大而横向TEC(α2)越小。这是由于径向模量增大，纤维在径向的残余压应力也会增大而导致该方向的压缩效应增强；与此同时，纵向泊松膨胀效应也随之增强。

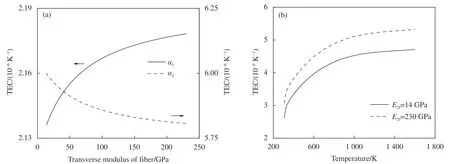
图10 纤维径向模量对Mini 复合材料(a)及2D-C/SiC 材料(b) TEC 的影响Fig.10 Effect of fiber radial modulus on TEC of minicomposites (a) and 2D-C/SiC (b) composites

大多数碳纤维材料都具有显著的各向异性，在沿纤维方向具有很高的刚度，而垂直于纤维方向的刚度较低，以T300 碳纤维为例，其纵向模量高达230 GPa，而径向模量不及其1/10。图10(b)给出了纤维径向模量取230 GPa 和14 GPa 两种情况下2D-C/SiC 材料表观TEC 的变化趋势，其中τ=10 MPa，L=400 µm。可以看出，若考虑纤维的横观各向同性，材料的表观TEC 会明显降低。经计算发现，表观应变εL与副泊松比ν21呈现显著的正相关性，而ν21与表观横向模量ET成正比，ET又随E2f的增大而增大，因此，E2f较大时表观TEC 的预测值也增大。

4.2.2 基体模量和孔隙率的影响

通常，高纯高致密的多晶化学气相沉积(CVD) SiC (假设为无孔隙材料)的弹性模量最高，为460 GPa[40]，但对于陶瓷基复合材料，CVD 工艺直接影响了材料的致密化过程，不可避免地会引入大量孔隙而导致材料的致密度降低。从微观角度分析，这些孔隙的存在削弱了原子间的键合强度，从而使SiC 基体的弹性模量有所降低，对结构性能产生一定影响。室温下的弹性模量E可表示为孔隙率Vp的指数函数：

可以看出，孔隙率增大，基体弹性模量随之下降。当2D-C/SiC 的密度为1.8 g/cm3时，其孔隙率为25.75%，根据式(58)，此时基体模量将折减到180 GPa。

图11(a) 给出了基体模量对Mini 复合材料纵向及横向TEC 的影响，其中τ=10 MPa，L=400 µm。可以看出，基体模量越大，纵向热膨胀系数越高而横向热膨胀系数越低，且基体模量对前者的影响更为显著。

图11 基体模量对Mini 复合材料(a)及2D-C/SiC 材料(b) TEC 的影响Fig.11 Effect of matrix modulus on TEC of minicomposites (a) and 2D-C/SiC composites (b)

图11(b)给出了基体模量取350 GPa 和180 GPa两种情况下2D-C/SiC 复合材料表观TEC 的变化趋势，对应孔隙率分别为7.6% 和25.75%，其中τ=10 MPa，L=400 µm。可以看出，若考虑孔隙率对SiC 基体模量的影响，材料的表观TEC 将有所下降[41]，这也在一定程度上解释了图8 中T2 试件TEC 值低于T1 试件的原因。从本质上讲，低温阶段的部分热膨胀变形需要填充材料的内部孔隙，因而对表观热膨胀变形没有贡献。因此，孔隙一定程度上会使模型TEC 发生折减，此时可对式(4)进行简单修正，给出

其中，a、b为拟合系数，且有a=1 450 K，b=0.63。当综合考虑孔隙对表观TEC 的折减效应时，模型给出的预测曲线与试件T2 数据更为吻合，见图12。

图12 考虑孔隙率Vp 的2D-C/SiC 表观TEC 预测曲线Fig.12 Predicted curve of apparent TEC of 2D-C/SiC considering porosity Vp

4.2.3 界面滑移应力和基体裂纹间距的影响

当环境温度为1 000 K 时，界面滑移应力对Mini 复合材料纵向以及径向TEC 的影响规律如图13(a) 所示，其中L=400 µm。可以看出，随着界面滑移应力的增大，α1和α2均呈现出增大的趋势，这是由于界面摩擦效应增强而导致界面载荷传递效率提高，即损伤效应占比变小。

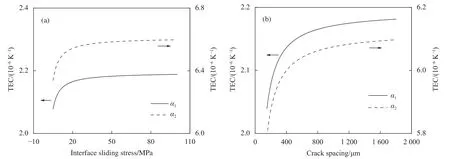
图13 界面滑移应力(a)和裂纹间距(b)对Mini 复合材料纵向及径向TEC 的影响Fig.13 Effect of interface sliding stress (a) and crack spacing (b) on TEC of minicomposites

图13(b) 描述了基体裂纹间距对Mini 复合材料纵向及径向TEC 的影响，其中τ=10 MPa。与界面滑移应力τ相似，裂纹间距L越大，脱粘率越小，纵向及径向膨胀变形量就越大。当裂纹间距大于1 000 µm 时，两个方向的TEC 增长速率均变缓，最终趋于稳定，此时模型将给出趋近于无损状态的热膨胀系数演变曲线，见图8。

本文模拟计算中，取界面滑移应力为10 MPa、裂纹间距为400 µm，此时界面脱粘率仅为15%，因此，基体开裂和界面脱粘对热膨胀变形的影响并未凸显出来。

从图13 还可以看出，界面滑移应力和基体裂纹间距对Mini 复合材料TEC 的影响规律相似，其影响机制也相似，都是通过改变界面脱粘率的大小而改变表观TEC 的变化趋势。

图14 给出了界面滑移应力及裂纹间距对2DC/SiC 复合材料表观TEC 的影响规律，图14(a)中参数L=400 µm，图14(b) 中参数τ=10 MPa。可以看出，界面滑移应力和裂纹间距较小时，界面脱粘率较大，此时改变这两个损伤参数对表观TEC曲线的影响较为明显。

图14 界面滑移应力τ (a)和基体裂纹间距L (b)对2D-C/SiC 表观热膨胀系数的影响Fig.14 Effects of interface sliding stress τ (a) and matrix crack spacing L (b) on apparent TEC of 2D-C/SiC composites

4.2.4 基体热膨胀系数的影响

对于β-SiC 基体材料，Rohm 等[40]测得了其在室温至1 273 K 范围内的TEC；而Taylor 等[42]利用X 射线法得到了其在室温至1 473 K范围内的TEC。将这些测量结果与式(56) 的值进行对比，发现不同工艺制备的SiC 材料其TEC 差异较大，如图15(a)所示。

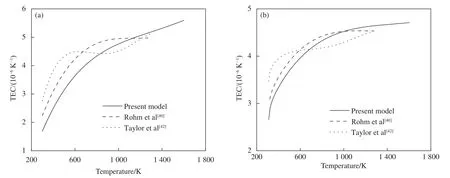
图15 SiC 基体(a)和2D-C/SiC (b)表观TEC 随温度的演变规律Fig.15 Evolution behavior of TEC of SiC matrix (a) and 2D-C/SiC (b) with temperature

图15(b) 给出了基体TEC 不同时2D-C/SiC 表观TEC 随温度的演变行为，其中τ=10 MPa，L=400 µm。对比发现，表观TEC 的变化特征与基体TEC 的变化规律相一致。以Taylor 曲线为例，SiC的TEC 在低于500 K 时迅速增加，在500～900 K 范围内基本保持为常量，在900 K 以上时再次快速增大，而其对应的表观TEC 随温度也有相似的3个变化阶段。这种相互契合的演变关系表明基体热膨胀系数是影响材料表观热膨胀系数的关键因素。