基于MFO-BPNN的螺旋钻机钻速预测研究*

2024-04-24李嘉辉郑荣跃赵京昊

机电工程 2024年4期

李嘉辉,王英*,郑荣跃,叶军,赵京昊,陈立

(1.宁波大学机械工程与力学学院,浙江宁波 315211;2.宁波大学土木工程与地理环境学院,浙江宁波 315211;3.浙江工业职业技术学院机电工程学院,浙江绍兴 312000;4.浙江易通特种基础工程股份有限公司,浙江宁波 315800)

0 引言

螺旋钻机是一种用于成孔作业的桩工机械,主要用于建筑物、桥梁、码头等桩基础工程。它通过旋转钻杆驱动钻头在地下进行钻孔作业,其作业效率的重要指标在于对钻速的精细控制。

DENG Y等人[1]基于岩石破碎能耗预测模型,提出了钻速预测方程,预测的平均误差低于15%;但该方程属于经验公式,是基于已有实验和观察结果得出的,不能很好适用于新的地质条件。HUNG N V等人[2]通过分析岩石物理力学性能、钻具参数等因素,建立了钻进过程的数学预测模型;但钻速预测属于复杂非线性问题,使用数学模型进行简单预测,往往难以准确表达钻进整个过程。

近几年,国内外的研究学者利用机器学习算法,对石油钻井工程中的机械钻速进行了一系列研究并取得一定的成果。

MATINKIA M等人[3]使用卷积神经网络(convolu-tional neural network, CNN)建立了钻井速率预测模型,相对于传统的回归模型,CNN模型具有更好的性能;但它需要更多的计算资源和时间。许明泽等人[4]提出了一种使用多模型集成学习来预测机械钻速的方法,相比于单个模型预测和传统的加权平均方法,取得了更好的预测效果;但需要训练多个模型来进行集成。李琪等人[5]提出了一种基于PSO-BPNN的机械钻速预测模型,预测结果准确率达90%以上;但李琪等人没有将该效果和其他优化方法的效果作比较。

然而,基于桩基础工程的钻速预测研究相对有限。通常情况下,钻井工程是在数千米的坚硬地层上进行打孔[6],岩性较为单一。而桩基础工程则主要是在距离地表100 m内的松散土层中打孔,土壤类型和土层构造复杂多变,导致钻速波动较大。此外,钻速还受到多种因素的影响,包括钻孔深度、钻杆转速、液压泵排量和岩石强度等,用数学方法建立一个能够准确预测钻速的非线性模型相当困难。

表1 部分钻探参数

因此,寻找合适算法提高神经网络模型的自适应性,以取代人工干预钻速控制,对钻机速度的智能控制具有重要工程意义。

笔者将MFO算法应用于调整BPNN的权值和阈值,提出一种基于MFO-BPNN的螺旋钻机钻速预测新方法,以江苏无锡市某公司厂区建设项目为例,利用某公司ZM80中置螺旋钻机试验台,对获取的钻探数据进行现场应用,并将其与BPNN模型、GA-BPNN模型以及PSO-BPNN模型比较,验证其预测的精确性与泛化性。

1 方法概述

1.1 MFO算法

近年来,研究人员受到自然界生物活动启示,提出了群体智能优化算法。例如PSO算法[7-8]、蚁群优化算法(ant colony optimization, ACO)[9]。受飞蛾行为的启发,澳大利亚学者MIRJALILI S[10]于2015年提出了一种智能优化算法——MFO算法。

MFO算法中采用基于火焰的位置更新机制[11-13]。首先,初始化一定数量的飞蛾,并为网络随机分配初始权重和阈值;然后,计算适应度,即对于每个神经网络,采用给定的训练集计算并记录输出误差,根据适应度,更新每个飞蛾的位置。若某个飞蛾的适应度较高,则它的位置保持不变;反之,则将其位置向更适合解决问题的位置移动一定距离。

位置更新公式如下:

Mi=S(Mi,Fj)

(1)

S(Mi,Fj)=Diebtcos(2πt)+Fj

(2)

Di=|Fj-Mi|

(3)

式中:Mi为飞蛾;Fj为火焰;S为飞蛾螺旋飞行函数;Di为火焰与飞蛾的距离;b为螺旋常量;t为[-1,1]之间的随机数。

笔者按适应度重新排序更新后的飞蛾和火焰位置,选择适应度更佳的位置作为下一代火焰的位置进行更新。随着迭代的进行,火焰数量将自适应地减少。

其数量公式表示如下:

Fnum=round(N-l(N-1)/T)

(4)

式中:Fnum为火焰数量;N为飞蛾种群数;l为当前迭代次数;T为最大迭代次数。

当火焰减少,飞蛾数量会大于火焰数量,多出来的飞蛾会根据当前适应度最差的火焰来更新其自身位置;当达到预设迭代次数或者适应度值已经满足要求时,结束算法,输出适应度最好的神经网络的权值和阈值。

1.2 MFO算法优化BPNN

BPNN是一种常用的人工神经网络模型,广泛应用于模式识别、数据挖掘、预测分析等领域。

笔者采用了BPNN作为基础模型,其结构如图1所示。

图1 典型BPNN结构

BPNN的训练算法是梯度下降法[14-15],它是根据误差函数对权值和阈值求偏导数,沿着负梯度方向更新参数,使误差函数最小化。

梯度下降法的更新公式为:

(5)

(6)

式中:wij为第i层第j个节点到第i+1层第k个节点的权值;bi为第i层第j个节点的阈值;η为学习率;E为误差函数。

在训练BPNN时,可能面临陷入局部最优的问题。此外,在BPNN模型中,初始权重和阈值一般是随机化的,会导致网络出现振荡或不收敛等现象[16]。

将MFO算法应用于BPNN中,可以有效地优化神经网络的权值和阈值,加速收敛并改善模型的拟合效果[17-18]。

其训练流程如图2所示。

图2 MFO-BPNN训练流程

2 钻探数据采集与分析

2.1 工程地质条件

拟建工程位于江苏省无锡市新吴区,场地地貌单元为太湖水网平原区的水网平原,地势较为平坦。场地及临近地区无活动断裂,无岩溶、滑坡、崩塌、泥石流、采空区等不良地质作用,除对局部场地浅部厚填土区应进行必要的处理外,其他地基土层分布较均匀、稳定,不存在能导致场地滑移、大的变形和破坏等严重情况的地质条件,场地整体较稳定,适宜建筑。

该场地的施工图如图3所示。

图3 某公司ZM80中置螺旋钻机钻进中的施工现场

场地土类型为中软土,勘察场地所在区域的覆盖层(剪切波速小于500 m/s的岩土层)厚度大于50 m,故该工程的建筑场地类别为Ⅲ类,设计特征周期为0.45 s。

该项目施工地XJ59、CZ21两个勘探孔的地质参数如图4所示。

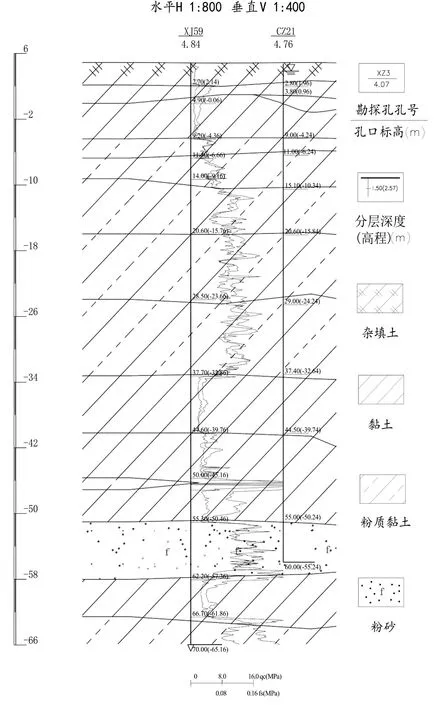
图4 施工地的工程地质剖面图

由图4可见:两条曲线分别代表锥尖阻力和侧摩阻力,用于划分土层和估算单桩承载力。两个勘探孔深度较大,土层种类较复杂。地表分布的杂填土,结构松散,工程力学性质均匀性差。埋深1.5 m～3.5 m段分布的褐黄色粉质黏土,可塑状,工程力学性质尚好。3.5 m～34 m段为黏性土层,根据土层埋深和性质特征,可细分为可塑状灰黄色粉质黏土、软塑状灰兰色粉质黏土、可塑状灰黄、灰兰色粉质黏土;其中,灰黄色粉质黏土的工程力学性质较好,可作为荷载不大的拟建物天然地基的基础持力层。一般埋深34 m以下分别为灰褐色粉质黏土(软,可塑状,工程力学性质良好)、灰色粉砂(密实,工程力学性质良好)、灰兰色粉质黏土(硬可塑状,工程力学性质良好),均可考虑作为单柱荷载很大的拟建物钻孔灌注桩的桩端持力层。

该项目采用钻孔灌注桩工艺,可选择灰色粉砂层底部为桩端持力层,采用Φ800钻孔桩,桩端入土深度在40 m左右,并辅以桩端后压浆措施。

2.2 数据采集与分析

钻探数据来源于施工现场多口深度在40 m～50 m的孔洞,采用分布在螺旋钻机上的传感器、数据采集系统等设备采集。钻杆转速和扭矩采用传感器和钻杆监控系统来实时采集并记录。可利用测量液压马达的脉冲信号,并经过一定的公式换算,得出钻进深度。泵压采用压力传感器MIK-P300-40 MPa来采集。

该设备的实物图如图5所示。

图5 液压泵压力传感器

笔者将采集的数据分为两组,命名为训练集与测试集。经初步整理后建立数据库,整个数据库拥有近1 000组数据。

部分数据样本如表1所示。

由表1可知:螺旋钻机钻速受多种因素影响,其中包括深度、扭矩、转速、钻压、排量、岩石强度和泵压等。

通常情况下,较高的转速和扭矩会导致较快的钻速,但其过高可能会造成钻头磨损和过热的问题。钻压和泵压适度提高可以提高钻速,但其过大可能会导致钻头磨损、振动增加,从而影响钻孔质量。通过增大岩石强度会增加钻进阻力,从而降低钻速。通过增加排量可以提高液压系统的效率,进而提高钻速。随着钻进深度的增加,钻速会下降。根据这些影响因素实时调整钻速,才能获得最佳的钻进效果。

3 神经网络模型建立

3.1 数据预处理

采集的钻探数据中包含一些重复或者异常的数据点,这些数据点称为噪声。噪声会影响数据的准确性,导致模型训练不稳定或者产生不良的预测结果。

小波阈值降噪是一种基于小波变换的信号降噪技术,其核心思想是将信号分解成不同尺度和频率的小波系数,然后通过滤波处理去除噪声信号,最后将处理后的小波系数重构成降噪后的信号[19]。

使用软阈值去噪后的数据曲线如图6所示。

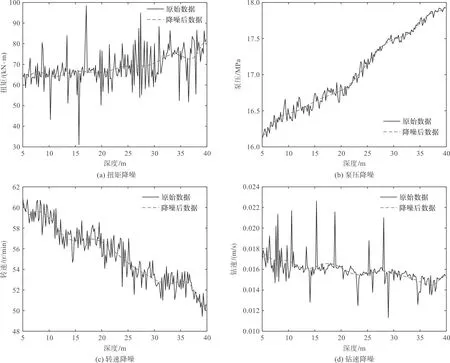
图6 部分数据小波阈值降噪前后对比图

由图6可见:图6(a)中扭矩的震幅较大,增长较为平稳;图6(b)中泵压呈小幅波动增长;图6(c)中转速呈中幅波动减小;图6(d)中钻速的变化总体上逐渐下降,呈不规则震荡趋势。

此外,在深度最大的地方,上述4幅图均显示了不同幅度的波动。经降噪,消除了一些异常数据,且保持了原有的趋势和特征。

为了获得更精确的预测结果,需要对数据进行归一化处理。由于钻速和输入数据的数量级相差较大,这可能会对网络的预测能力产生影响。因此,笔者使用MATLAB中的mapminmax函数来对数据进行归一化处理,将归一化后的数据范围限定在[0,1]之间。

其转换公式为:

(7)

式中:x′为归一化后的值;x为样本数据的初始值;xmax为最大值;xmin为最小值。

归一化后的数据如表2所示。

表2 归一化后的钻探参数

在完成预测后,笔者对经过归一化处理的数据进行反向归一化操作,以恢复它们的原始数值范围。反归一化操作是通过postmnmx函数实现的。

笔者随后进行参数相关性分析,筛选出钻速预测模型的输入参数。灰色关联度[20]反映了各因素之间的相似程度和影响程度,值越大表示影响越大。

首先,确定分析序列:将数据分为母序列与子序列,其中,母序列为能反映系统行为特征的数据序列,类似因变量Y,记为:

Y=[y1,y2,…ym]T

(8)

式中:Y为钻速序列。

子序列指的是影响系统行为的因素组成的数据序列,类似因变量X,记为:

(9)

式中:n为样本的数量;m为要素的数量。

随后,计算子序列中各个指标与母序列的灰色关联系数。分别计算两极差,记两极最小差为a,两极最大差为b,表示如下:

a=minmin|yk-xik|,i=1,2…m

(10)

b=maxmax|yk-xik|,k=1,2…n

(11)

利用两极差计算灰色关联系数:

(12)

式中:ρ为分辨系数,一般取0.5。

最后进行灰色关联度值计算:

(13)

计算结果如图7所示。

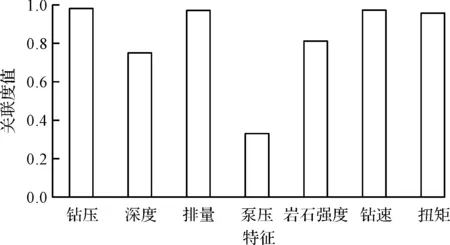
图7 钻速与其他特征参数的灰色关联度分析

将深度、钻压、转速等特征参数作为输入进行灰色关联度分析。

由图7可得:泵压与钻速的相关性较差,故予以剔除。

3.2 钻速预测模型构建

在数据预处理过程中,笔者将钻机的转速、深度、钻压、排量、岩石强度和扭矩作为神经网络的6个输入参数,钻速作为唯一的输出参数。因此,神经网络输入输出结构为6-1模式,使用MATLAB中size函数直接获取。

隐含层节点数量参考经验公式表示如下:

n=2m+1

(14)

式中:n为隐含层节点数量;m为输入层节点数量。

本次隐含层节点数选择13个,故网络结构为6-13-1模式。BPNN使用MATLAB中的神经网络工具箱建立。

参数设置如表3所示。

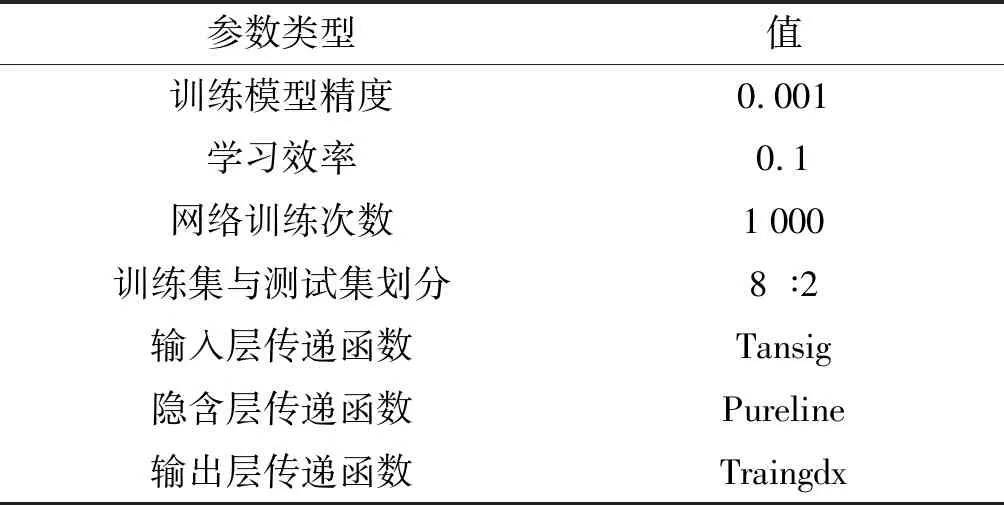
表3 BPNN参数设置

笔者利用GA算法、PSO算法以及MFO算法代替梯度下降法训练神经网络的权值和阈值。

其训练参数设置如表4所示。

表4 训练参数设置

笔者采用小波降噪、归一化和关联度分析等方法对现场采集的数据进行预处理;然后,建立MFO算法优化的BPNN模型,对800组训练集数据进行训练,得到了钻速预测模型。

该模型的框架结构如图8所示。

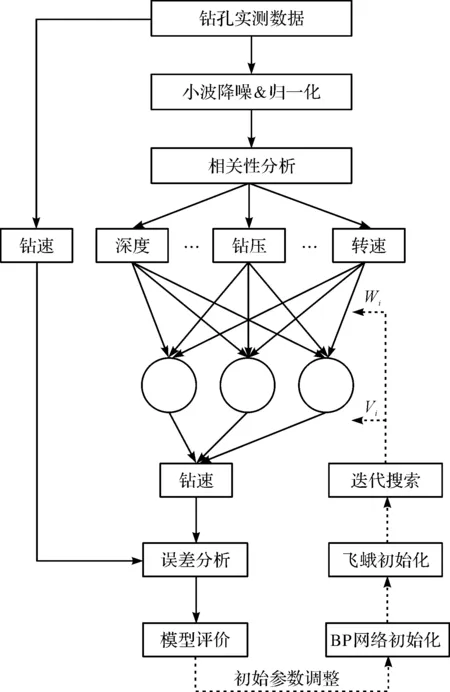
图8 MFO-BPNN钻速预测模型框架结构

4 测试与分析

800组训练集数据经过4种神经网络模型的训练,得到的结果如图9所示。

图9 各模型算法迭代过程

由图9可得:经过算法优化的BPNN的收敛速度都有所提高。其中,MFO-BPNN模型的收敛速度表现最佳,在36次迭代后其RMSE趋于平稳。

这证明了该算法具有良好的收敛性能。

200组测试集数据分配用于检验该预测模型的泛化能力。笔者随机取某一孔洞的37 m～38.5 m深度段的数据,展示测试成果。

四个模型的预测结果中,预测值和真实值的对比如图10所示。

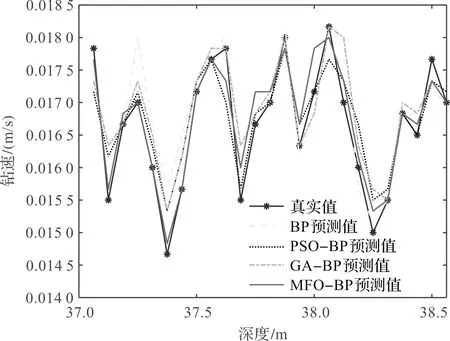
图10 预测值和真实值的对比

预测偏差对比如图11所示。

图11 预测偏差对比

由图10、图11可见:MFO-BPNN模型的预测曲线与实际曲线较吻合,相比BPNN模型、GA-BPNN模型和PSO-BPNN模型,具有更高的准确度。

通过比较偏差曲线可知,表示MFO-BP预测数据的曲线相较于其他曲线更加接近于零,说明该模型误差较小。

当评估回归预测模型的性能时,通常会使用损失函数,笔者采用平均绝对误差(mean absolute error, MAE)、均方根误差(root mean square error, RMSE)和平均绝对百分比误差(mean absolute percentage error, MAPE)来衡量预测结果与实际值之间的偏差程度;同时,使用R2来评估预测准确率。

预测准确率结果如表5所示。

表5 预测指标

由表5可知:MFO-BPNN模型的误差指标分别为0.012、1.201 8和0.016 5,比其他三个模型都要小;R2作为评价预测模型优劣的常用标准,MFO-BPNN模型的R2达到了0.916 5,这个值比BPNN模型高出18.9%,比PSO-BP模型高出9.5%,比GA-BPNN模型高出13.7%。

这说明预测模型与钻速值的拟合程度非常好。

为更直观展示4种模型的预测效果,笔者绘制了预测钻速与实际钻速的关系图。

预测值和真实值的关系如图12所示。