考虑结合面特性影响的机床整机有限元静力学分析模型*
2024-04-24黄为彬
王 豪,黄为彬,方 兵*
(1.福建农林大学 机电工程学院,福建 福州 350002;2.福建省农业信息感知技术重点实验室,福建 福州 350002)
0 引 言
目前,基于计算机辅助设计的理念已经广泛地应用于精密数控机床产品的开发中。设计者期望在设计阶段准确掌握产品的刚度、热特性、动态响应以及加工精度等性能。但由于机床零部件数量众多、结构复杂,存在多种类型的结合面;结合面不连续的特点对机床刚度、热传导特性的影响显著,且结合面自身的影响因素较多、规律不明显。因此,结合面的建模准确与否在较大程度上影响整体分析的结果[1-3]。
在处理结合面问题时,“弹簧-阻尼”法是常用的方法之一。该方法用若干个“弹簧-阻尼”单元来模拟结合面的静、动态特性。如朱坚民等人[4]使用了“弹簧-阻尼”单元模拟主轴刀柄结合面,并进行了动力学参数识别,结果表明实验值与计算值相对误差在4%以内,具有较高精度。李院生等人[5]采用了4节点的“弹簧-阻尼”单元模型来等效结合面,解决了螺栓固定结合面参数识别问题。兰国生等人[6]采用了“弹簧-阻尼”法,建立了固定结合面法向接触阻尼模型及结合面间阻尼损耗因子模型。
然而“弹簧-阻尼”单元法存在一些缺点。该方法是一种简化自由度的方法,需要根据具体的问题,选择单元的数量,确定单元的位置,并且忽略了各单元之间的相互影响。
为了解决上述问题,近年来研究人员已经开始采用虚拟材料法建立固定结合面模型。
虚拟材料法是一种根据结合面接触部位微观结构,采用具备弹性模量、泊松比以及密度的材料来模拟结合面静力学和动力学特性的方法。比如,张学良等人[7]提出了一种利用宏观各向同性虚拟材料等效的固定结合部动力学参数化建模方法,即采用虚拟材料的弹性模量、泊松比等来模拟结合面静力学和动力学特性,结果显示,计算值与实验值的绝对误差在10%以内。孙伟等人[8-9]采用了一层虚拟材料来对含螺栓复合材料结构进行动力学分析,均达到了较高的精度。
然而,上述研究并未考虑弹塑性变形对虚拟材料属性的影响。
因此,笔者基于Greenwood-Williamson(G-W)接触分析模型,考虑弹塑性变形的影响,依据粗糙表面形貌统计参数,提出一种新的考虑摩擦力影响的刚度模型;根据结合面的刚度特性,将结合面等效成一层虚拟材料,建立固定结合面的静力学分析模型,将其应用于整机的有限元分析,并且开展机床静刚度测试实验,以验证上述分析结果的正确性。
1 结合面虚拟材料模型
结合面实质上是由两个相互接触的粗糙表面组成,可以将其简化为一个粗糙表面与一个刚性平面接触。
GREENWOOD J A等人[10]早在20世纪60年代就提出了基于统计理论的G-W接触分析模型。该模型假定凸峰的高度服从某种特定的分布(如高斯分布),凸峰具有相同的曲率半径。当凸峰的变形量ω大于弹性极限值ωe时,凸峰开始呈现塑性变形的特点。然而,KOGUT通过有限元分析的方法发现,凸峰由弹性变形阶段开始进入塑性变形阶段时,先要经历一个弹塑性混合变形阶段;然后,直到其变形量大于等于110×ωe时,凸峰才呈现完全塑性变形的特点[11]。因此,单个凸峰的接触过程可由弹性、弹塑性和塑性三个阶段来描述。
1.1 弹性接触变形
根据Hertz接触理论,可建立弹性接触面积ae、弹性接触载荷pe,以及弹性变形量ω间的关系如下:
ae=πRω
(1)
(2)

当结合面间存在摩擦力时[12],由凸峰发生屈服的临界平均接触压力pave=kυkμH可得到弹性变形极限,即:
(3)
式中:kυ为平均接触压力系数,由材料泊松比υ确定[13],kυ=0.464 5+0.314 1υ+0.194 3υ2(若取υ=0.3,则kυ≈0.6);kμ为摩擦力影响系数,其值与摩擦系数μ有关[9];H为材料硬度。
kμ的计算公式如下:
(4)
式中:μ为摩擦系数。
(5)
根据文献[14]可知,单个凸峰的切向刚度为:
(6)
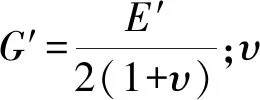
Qe和Pe分别表示该阶段的总体切向载荷和法向载荷,其中:
(7)
式中:η为凸峰密度;A0为名义接触面积;z为凸峰高度;d为刚性平面与粗糙表面中线的距离,且满足关系式:ω=z-d;ωe为弹性极限值;φ(z)为高度分布的概率密度函数。
文献[15]给出了单个凸峰所承受的切向载荷为:
(8)
式中:σy为与摩擦力方向相同的应力;a为接触点面积;p为接触点上的载荷。
根据接触面积与变形的关系,可得该阶段总切向载荷为:
(9)
1.2 弹塑性接触变形
当变形量在ωe和完全塑性临界值ωp之间时,微凸峰处在弹塑性混合变形阶段。
李玲等人[16]在接触面积、平均接触载荷满足连续变化的基础上,构造了以变形量ω为自变量的多项式表达式,其接触面积可表示为:
aep=πRκ1(ω)
(10)
其中:
接触载荷可表示为:
(11)
类似的可定义刚度为接触载荷对变形量的导数,于是法向接触刚度可以表示为:
(12)
其中:
κ3(ω)=-2g3(ω)+6(2-ω)g2(ω)+2(3ω-4)g(ω)+2。
则,切向接触刚度可以表示为:
(13)
式中:Pep,Qep为该阶段的总体切向载荷和法向载荷。
Pep和Qep表达式如下:
(14)

(15)
1.3 塑性接触变形
KOGUT L等人[11]通过有限元计算发现,当变形量ω大于110×ωe时,凸峰呈现完全塑性变形的特点。此时,接触面积、载荷与变形量的关系可以表示为:
ap=2πRω
(16)
pp=Hap
(17)
类似的,可以求得该阶段的法向接触刚度和切向接触刚度分别为:
(18)
(19)
Pp和Qp表示该阶段的总体切向载荷和法向载荷,分别为:
(20)
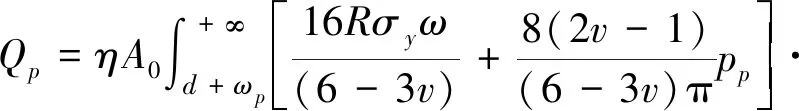
(21)
综合式(5)、式(12)和式(18),可得到总的法向接触刚度为:
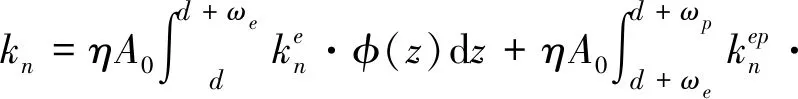
(22)
综合式(6)、式(13)和式(19),可得到总的切向接触刚度为:
(23)
1.4 虚拟材料属性确定
采用虚拟材料模拟结合面的静力学特性,需要知道虚拟材料的密度ρ(取两接触材料的平均密度)、弹性模量Ev、泊松比μv、虚拟材料的面积A和厚度t等参数。
根据机械加工表面形貌特征以及有限元分析的需求,参考文献[17],可选取虚拟材料的厚度t为1 mm。
等效虚拟材料模型如图1所示。

图1 等效虚拟材料模型
若单位面积上的法向刚度和切向刚度分别为(量纲为[N·m-3]):
(24)
(25)
取一面积为ds的微元,在法向载荷Fn的作用下,其法向应力和应变分别为σ和ε,则有:
(26)
式中:δn为法向变形量。
由弹性模量定义及化简式(14),得到:
(27)
式中:Ev为虚拟材料的等效弹性模量。
同理,可得虚拟材料的等效切变模量Gv为:
(28)
式中:τ为切变应力;γ为切变应变。
泊松比μv为:
(29)
2 整机静刚度仿真分析
某立式加工中心的床身与立柱材料均为HT200,接触表面采用铣削方式加工。在机床X、Y、Z三个方向各布置一根丝杠分别用于驱动主轴箱、工作台和滑板。主轴前端安装锥度为7:24的BT50刀柄,轴承采用4+2的布置方式,即前端采用4列并列,后端采用2列并列的方式配置,型号分别为7020C和7018A。
笔者对模型进行必要的简化,并在CATIA V5r16中建立床身、立柱、滑板、工作台、主轴箱以及导轨等主要零部件模型,按设计尺寸装配成整机三维模型,再将CATIA V5r16中的整机三维模型导入ANSYS Workbench中,进行网格划分、参数设定以及边界条件设置等,以建立有限元分析模型[18]。
得到结合面的虚拟材料属性是建立整机静刚度分析模型的关键。此处以床身立柱结合面为列,该结合面由16只螺栓固定,正压力约为56 000 N,接触面积为0.238 m2,平均接触压力为2.35×105Pa。采用轮廓仪(泰勒霍普森Form Talysurf i120)测量所研究表面的形貌,并根据文献[19]所提供的方法,经计算得到服从高斯分布的表面凸峰的高度分布函数φ(z),平均半径β为42.68 μm以及单位面积凸峰个数N为8.45×103个/mm2。
平均接触压力Pav与弹性模量Ev的关系如图2所示。

图2 平均面压与弹性模量间的关系
由式(7)、式(14)、式(20)和高度分布函数φ(z)可得到总载荷P与偏差d间的关系,由式(24)和式(25)可分别得到弹性模量Ev、μv和偏差d间的关系。
综合上述两个关系,便可得到平均接触压力Pav与弹性模量Ev。随着平均接触压力Pav的增加,虚拟材料的弹性模量也在增加,但趋势趋于缓慢。
所建立的有限元分析模型主要考虑了床身立柱结合面、轴承内圈与主轴的结合面、轴承外圈与箱体的结合面,以及主轴前后两个端面;轴承、丝杠以及导轨则采用弹簧单元法进行等效。
根据实际工况,可得到主要结合面的虚拟材料参数如表1所示。
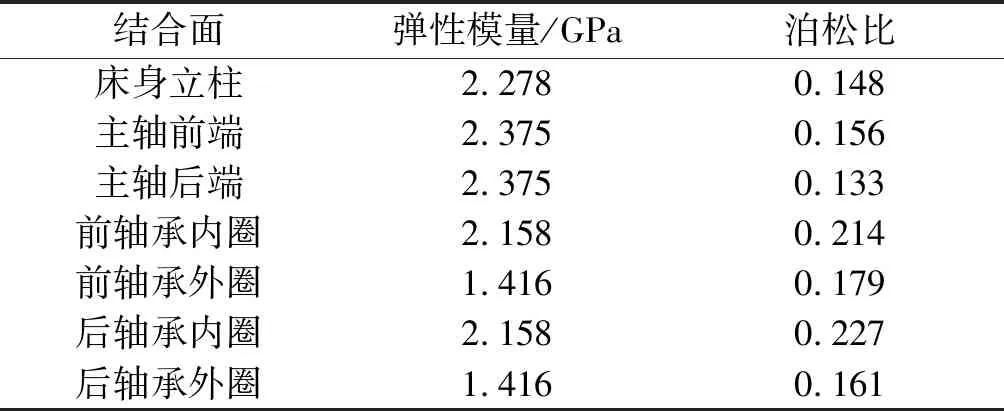
表1 主要结合面的虚拟材料属性
仿真计算时,在主轴刀柄下端面沿着X、Y、Z三个方向施加大约1 960 N的载荷,反向载荷施加在工作台面相应位置上,并将床身底座与地面的接触面固定约束。
仿真结果如图3所示。

图3 施加1 960 N载荷的整机变形
可见,主轴在承受载荷时,变形主要体现在主轴及其周边的零部件,其中主轴前端影响最为明显。在相同的载荷作用下,X、Y和Z方向的位移分别为68.6 μm、44.5 μm和47.3 μm,三个方向对应的刚度分别为28.57 N/μm、44.04 N/μm和41.43 N/μm。总体来说,Y方向的刚度最大,Z方向上的刚度次之,X向刚度最小。
3 实验与比较
为验证整机静刚度有限元分析结果的正确性,笔者开展了机床静刚度测试实验。
实验测试原理如图4所示。
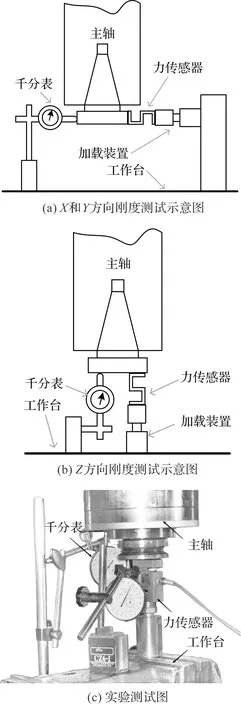
图4 机床静刚度测量
笔者将机床各零部件放置在与仿真分析时对应的位置上,以98 N为间隔逐步增加载荷至1 960 N,采用精度为0.98 N的BK-2型压力传感器测量载荷,由二次仪表显示测量结果,采用分辨率为2 μm的千分表测量相对变形。
实验结果如图5所示。
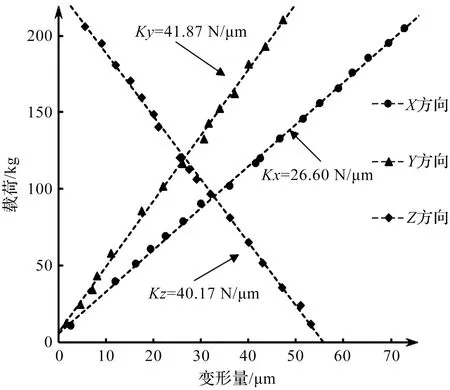
图5 载荷-变形曲线
随着外加载荷的增加,主轴末端的相对变形也在逐渐增加,测得的“载荷-变形”数据基本呈线性规律。可拟合得到X、Y、Z三个方向的刚度,分别为26.60 N/μm、41.87 N/μm和40.17 N/μm。
为研究结合面对整体刚度特性的影响,笔者对未考虑结合面特性的模型进行分析计算。所谓不考虑结合面是指忽略由连接部位(也就是结合面)引起的刚度的变化。
在有限元模型中,笔者直接将连接部位黏接成一体,使得结合部与被连接部件的材料属性一致。
实验结果与仿真结果如表2所示。

表2 整机静刚度仿真与实验对比
其中,仿真的结果分为两个模型,一个是考虑了结合面影响的模型,另一个是没有考虑结合面影响的模型。
对比结果表明:不考虑结合面的影响时,机床工艺系统的静刚度与实验值的相对误差达到17%左右;考虑结合面影响之后,其相对误差基本在5%以内。以上结果验证了所提出模型的准确性。
4 结束语
针对机床数字化设计中典型结合面建模精度误差较大的问题,笔者提出了一种采用虚拟材料等效结合面静力学特性的方法,建立了考虑结合面特性影响的机床整机有限元静力学分析模型,并完成了相应的静刚度测试实验。
笔者基于粗糙表面接触理论,推导了考虑摩擦力影响的固定结合面的法向刚度和切向刚度解析表达式,并确定了用于模拟结合面静力学特性的虚拟材料的等效弹性模量和泊松比。
研究结果表明:
1)机床典型结合面等效后的虚拟材料弹性模量较基体材料小1到2个数量级。因此,对整机分析时,必须考虑结合面的影响;
2)与实验测试结果对比,不考虑结合面影响的机床整机有限元静力学分析模型的误差在13%~17%之间,与实际偏差较大;
3)考虑了结合面特性影响后,得到机床整机有限元静力学分析模型的误差基本在5%以内,精度满足工程设计的要求。
目前,笔者主要采用虚拟材料法研究了结合面的静力学特性。后续工作中,笔者将在本研究的基础上,将该模型应用于结合面的动态特性以及热-结构耦合分析等方面。
