生态位的T-S模糊滑模自适应控制
2024-04-22郝云力王茂华
郝云力,王茂华
(1.阜阳师范大学 信息工程学院,安徽 阜阳 236041;2.阜阳师范大学 数学与统计学院,安徽 阜阳 236041)
0 引言
生态位在生态系统中占有很重要作用[1],是理论研究生态系统和种群动力学以及实际应用中的主要方向。生态学和种群动力学在根本上是整体和非线性的,在一个系统中,不同的生命、群体之间不能相互分离,是一种复杂不确定非线性的关系[2]。传统的生态系统建模已不满足描述和研究现有的生态系统进化的极高复杂非线性,模糊建模具有的优势恰好能解决这个问题而成为研究的热点[3]。李医民等[4]在2005年首次将生态系统中的生态位概念抽象出来,建立具有量化效果的模糊几何和代数数学模型,进而建立生态位的态、势模糊数学模型,又利用复杂网络方法给出从生态位的个体竞争到种群竞争模糊数学模型,进一步丰富生态位研究模型,对生态系统的非线性分析和量化工作具有十分重要的实践意义。
生态系统中的生物个体和群体进化具有自适应、自组织的特性,因此考虑将生物系统的非线性进化特性自适应性和稳定性与具有处理不确定性的模糊控制方法相结合[5],形成具有生物特性的控制方法和仿生方法。李医民[6]将生态位贴进度作为T-S模糊控制的后件,无需辨识参数,但缺乏精度。随后李医民等[7]又将生态位贴进度函数作为T-S模糊控制的后件,找到贴进度的生态因子自适应律,提高了仿真精度,但控制执行力不够。由于type-2型模糊系统具有较强的执行能力[8],将生态位贴进度应用到type-2型模糊系统中[9],给出生物个体和群体的动态生态位模型,但不能很好地处理高阶非线性系统。张发祥等[10]将生态位的态和势模型作为type-2型模糊控制的后件,能很好控制高阶非线性,还是没有对生态位控制思想处理到极致。郝云力等[11-12]提出将生态位贴进度函数与type-2型T-S模糊控制相结合,找到生态因子的自适应律,使仿生效果更进一步,但算法复杂。
滑模控制方法结构简单,对于外部扰动和参数不确定性具有较强的鲁棒性,能够有效抵抗外界扰动、系统参数变化的影响和实现系统状态的快速滑动和准确跟踪,越来越受到学者的关注[13]。滑模控制最早由EMELJANOV[14]提出,柏值等[15]对不确定性系统提出了一种鲁棒滑模控制方法,但系统状态在有限时间内收敛受到限制。后边针对滑模控制的缺点,大量的学者进行了研究[16-18],并取得一些研究成果。因T-S模糊控制的后件是一个多项式函数,可以精准的逼近非线性系统。T-S模糊滑模控制也受到大家的喜爱和研究。
生态位是整个生态系统的基础,它把生物的自适应、自组织和学习能力结合起来,构建出具有生物特征的模糊控制系统。本文提出将生态系统具有进化特性、自适应性和稳定性的生态位与T-S滑模控制相结合,构造具有生物特性背景的T-S模糊控制方法。具体是用生态位贴近度函数作为T-S模糊滑模控制的后件,建立李雅普函数,分析系统的稳定性和得到生态因子的自适应律,在此基础上,通过对生物的适应能力进行分析,并根据结果对其进行了相应的调节,以反映生物的自适应能力、自我发展能力以及生物利用环境的自学习发展水平,突出了本方法的仿生效果。
1 生态位控制
考虑如下形式的n阶非线性系统:
(1)
其中:u∈R和y∈R分别是系统的输入和输出;f(X;t)和b(X;t)为有界函数,且b(X;t)>0;d(X;t)是未知干扰,其绝对值小于已知的连续函数。
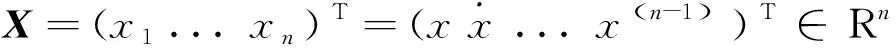
b(X)为非零的有限函数,因为f(X)和未知,用T-S模糊逻辑系统来估计。设模糊系统f(X)由一系列“如果-则”模糊规则构成:
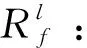
(2)

(3)
模糊滑模面定义为:
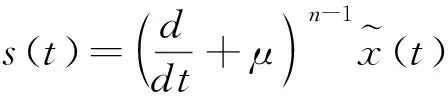
(4)
方程s(t)=0在Rn上定义了一个时变的超平面,在此超平面上跟踪误差向量以指数形式递减到0,维持此状态,可获得很好的跟踪性能,则有:
(5)

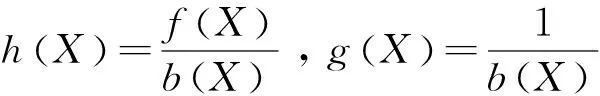

(6)
(7)
于是得到当控制增益不为1时的鲁棒自适应控制率
(8)

由公式(7)和公式(8)得到:
(1-m(t))(ufu-h-gar)+m(t)(usu-h-gar)+gd,
(9)
其中:ufu具体参见文献[11]。
则公式(9)可变为:
(10)
构造Lyapunov函数:
(11)
对公式(11)两边关于时间t求导得:

(12)
有自适应律为:
(13)

(14)
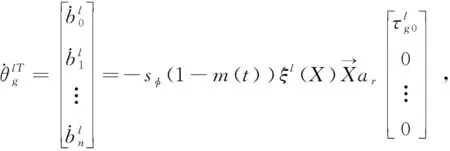
(15)
运用梯度下降法对公式(14)和公式(15)进行贴近度函数生态因子参数优化,k为步长,则
(16)
(17)
2 实例仿真
有二维捕食的模型为:
(18)
模型各参数和模型解释详由文献[8]知:
(19)
令
(20)


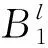
由公式(17)(19)和(20)得控制器
并设初始值x1(0)=0.3,x2(0)=4.0,φ=0.1,φ=0.01,则控制以后的系统图如图1、2所示。
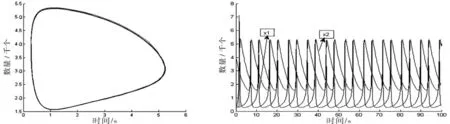
图1 系统相图 图2 控制后系统变量图
3 结论
生态位模糊数学模型对环境中个体的位置可以进行一个较好的描述,生态位贴近度又能反映生态系统的优劣,将生态位的贴近度函数与模糊滑模相结合,求出生态因子的自适应律,反映了生物个体追求理想生态位的结果,使本控制达到仿生智能作用。
