基于OAM 复用信号高效调制解调的声学超表面

刘 智,黄保霖,林 玮*,赵瑾瑜

（1.南京航空航天大学物理学院，南京，211106；2.安徽建筑大学数理学院，合肥，230601）

轨道角动量（Orbital Angular Momentum，OAM）作为声波基本且重要的自由度之一，可以提供不同的正交状态作为独立的信道，为大容量的声学通信提供更多的声学自由度，这适用于从自由空间到紧凑型的声学装置，在促进高速通信方面发挥着关键作用［1-4］.近年来，螺旋波前声涡旋束携带的OAM 成为信息编码的另一种自由度，为提高声通信的传输能力提供了巨大的动力，使用OAM 复用的高容量通信已在高频声学中得到了展示［5-7］.利用声波固有的物理特性，如频率和模态等，应用在声学复用技术中实现大容量数据存储，同时，基于角谱法和数字编码技术也实现了声学OAM 复用数据传输，并表现出较高的声学轨道角动量（Acoustic Orbital Angular Momentum，AOAM）复用和解复用效率.然而，承载OAM 波束的产生和检测大多基于体声学元件，由于其体积较大且存在频率带宽有限的固有缺陷，一般难以与其他微型系统集成，这对实现器件的微型化及集成化形成了挑战.此外，使用上述器件的系统，声能的传输效率通常也会受到限制，导致声涡旋场只能在短距离内保持稳定的拓扑数.因此，如何使用紧凑和非螺旋结构有效地产生稳定的AOAM 并应用到实际生活中是一个亟待解决的关键问题.

1 声涡旋场理论

声涡旋束早期被Nye and Berry［8］提出的时候就引起了广泛关注，其特点是围绕传播轴的螺旋相位错，涡旋声束的相位错可以用exp(imθ)来表征［9］.由于存在相位奇点，涡旋声束呈现独特的振幅分布，类似甜甜圈的形状.此外，许多特定的涡旋声束具有明确的径向强度分布.例如，贝塞尔式的径向压力分布可以描述如下［10］：

其中，Jm(krr)是第一类的二阶贝塞尔函数，kr和kz分别是径向和轴向波数.假设m1和m2为两个声学螺旋模态，其正交性可以通过两个不同模态的内积来证明［11］：

这一重要特征为编码信息提供了新的自由度，补充了已经被广泛采用的技术，包括幅度、相位、频率等.

产生声涡旋的基本原理可以利用式（3）描述：

其中，φout是出射声波的螺旋相位，φin是入射声波的相位.为了实现θ相关的螺旋相位φout，引入依赖角度θ的入射相位φin或操纵依赖于传播距离l的输入相位φin.通过声共振的设计引入依赖角度θ的有效波数keff来获得期望的声学涡旋场［12］.

我们将平面声共振层划分为不同的扇区，每个扇区包括多排径向排列的共振器，每排依次由四个亥姆霍兹共振腔和一个直管组成，这四个腔的组合排列可以被概念化为集总元件，能对入射声波进行相位调节［13］.每排的高度固定为0.1λ，壁的厚度设置为0.01λ.通过调节直管的高度来控制有效波数keff，保持单元尺寸不变，这便于单元的堆叠.采用四个亥姆霍兹谐振器串联，满足了传输性能的要求.

受到独立操纵的N个扇区的有效波数可以表示为keffj(j=1，2，…，N)，当N个有效波数取决于方位角θ时，实现所需的螺旋相位变得可行.在扇区内的多行共振器结构表现出近乎相同的传输特性的情况下，从扇区发出的声波在出射面得到的归一化声场可以近似为：

为了产生具有类似贝塞尔轮廓的声学涡旋束，出射波在具有半径为λ 的刚性波导内传播，其可以表示为圆柱贝塞尔模式的叠加［14］：

其中，Am，n为模态的振幅，Jm(km，nr)为m阶的贝塞尔函数，km，n为方程的第n个正根，轴向波数为方程（5）实质上体现了类贝塞尔声涡旋的特性.

2 仿真及结果

2.1 混合结构的构建利用混合结构组合传输单元，该结构包括深亚波长腔，这些腔是声学亥姆霍兹共振器，与位于这些亥姆霍兹共振器开口侧的直管配对，如图1 所示.谐振器作为集总元件，可以引入有效声阻抗用来改变入射声场的相位［15］.采用多个可调节高度的亥姆霍兹谐振器的串联结构来实现扩展相移到整个2π 范围，再将一系列亥姆霍兹谐振器与高度可调但固定宽度的直管相结合，利用形成的混合结构有效解决腔体与周围空气之间的阻抗失配，从而实现高传输速率.在特定的长度下，这种直管有效地匹配了声阻抗，利用法布里-珀罗谐振原理［16-17］，显著增强了声传输.这种混合结构设计使我们能够沿轴向保持深亚波长分辨率，即h≪λ.

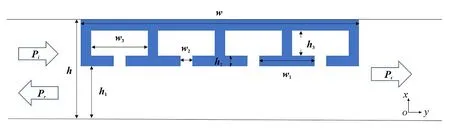
图1 由高度为h1的直管和四个高度为h3的亥姆霍兹谐振器组成的混合结构单元Fig.1 Hybrid structure element that consists of a straight pipe of height h1 and four Helmholtz resonators of height h3

图2 通过八个独立单元传输的仿真结果Fig.2 The simulation results of the transmission through eight independent components

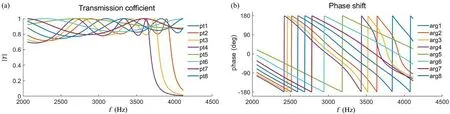
图3 (a)透射系数 |T |和(b)归一化有效波数的相移Fig.3 (a) The transmission coefficient | T |,and (b) the phase shift of effective wave number normalized

2.2 利用超表面产生声学OAM声学复用超构表面对声涡旋束的解复用机理是基于对超表面有效波数的操纵，这种操纵由Helmholtz 腔与直管之间的声混合共振引起，对于OAM 为-1 阶的声学复用超表面，八个部分中的期望有效波数keff应在-k～k，步长为，其中是背景介质中的波数.在该特定实现中，声学复用超表面的厚度和半径分别设置为0.5λ和0.3λ.每个区域包含沿着轴线分布的三组谐振器，其配置为具有四个亥姆霍兹腔和直管组合（图4）.

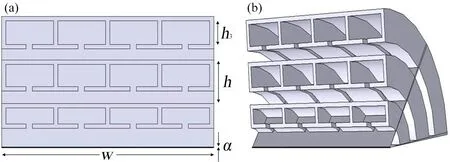
图4 单个单元结构的平面图(a)和单组声学超表面结构示意图(b)Fig.4 Plan of a single unit structure (a),and diagram of the acoustic metasurface structure (b)

在模拟仿真的设置中，将基于OAM 信号的声学复用超表面连接到圆柱形波导，两个探针按照预先设计的位置，探针1 位于超表面中心的前面，探针2 位于其后面.由于OAM 波束的轴处的零压力区域，每个探针（探针1 和探针2）仅能在它们各自的信道Chi(i=1，2)中捕获信息.入射信号是包括平面波和一阶OAM 波的复用波前，二者都从左侧发射.该复用信号被分成两个通道：将平面波指定为第一通道（Ch 1），而一阶OAM波束指定为第二通道（Ch2）.声复用超表面有效地将入射波的OAM 降低了一阶，因此，平面波转换为-1 阶的OAM 波束，并且一阶OAM 波束被转换成平面波，如图5 所示.

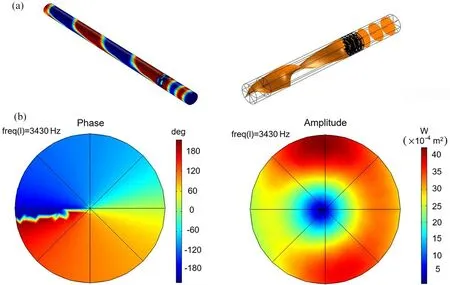
图5 (a)波导中声涡旋的产生（左）和传输（右）；(b)在3430 Hz 频率下产生的一阶声涡旋束在横截面处的相位分布（左）和归一化声压幅值（右）Fig.5 (a) Generation (left) and transmission (right) of the acoustic vortex in waveguide,(b) phases distributions (left)and Normalized sound pressure amplitudes (right) of the generated first-order acoustic vortex beam in the frequency of 3430 Hz at cross sections

2.3 声信号传输为了更加清晰地了解声复用超表面的运用，给出了复用的示例，其中，由幅度Am(t)和相位φm(t)表征的m阶AOAM 波束被表示为mth(Am(t)，φm(t)).使用多级相位和幅度格式将数据编码到AOAM 复用信号中.不同信号（对于i=1，2 表示为信号i）中的0 阶和1 阶OAM波束的幅度分别由探针1 和探针2 检测.

如图6 所示，探针2 检测到的接收信号显示π的相移，其精确地对应于图6a 和图6b 中的信号1和信号 2中的一阶OAM 波束之间的相位差.显而易见，图6c 和图6d 中的信号中的零阶 OAM 波束的幅度是信号 2中的一半，而零阶OAM 波束的相位具有相同的值.图6 展示了信号1 和信号2 的解复用，证明接收到的数据与最初编码到复用信号中的数据之间的良好匹配.

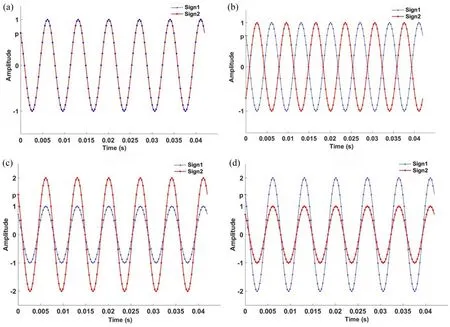
图6 探针接收的时域信号Sign1(带星号标记的蓝线)和Sign2(带圆圈标记的红线)Fig.6 The time domain signals received by probe 1 and probe 2，where Sign1 (blue lines with asterisk markers) and Sign2 (red lines with circle markers)

利用我们提出的多路复用方法，以声学轨道角动量为基础，促进有效的信号传输.为了直观地证明这一点，我们使用由字母“OAM”组成的图像作为传输的目标信号，并利用二进制差分相位编码将来自不同图像的信息嵌入到同时携带平面波和一阶OAM 的声涡旋模式中.

在这种编码方案中，将图像中的每个像素映射为二进制数，相位“0”和“π”分别由二进制数“0”和“1”表示.声波的调制是通过声脉冲实现的，入射载波的频率与声共振结构的特征频率相匹配，记为“f0=3430 Hz”（对应周期“T0”）.调制脉冲周期设置为“24T0”，占空比为0.5.每个调制脉冲内的声波初始相位作为二进制标识符，映射到研究中传输的图像像素.图7 显示了原始目标信号和接收信号在调制脉冲周期内的曲线，在理论推导中，采用角分辨谱法计算信息传输系统发射端需要激励的声载波信号的分布［18］.图8 是通过声学复用超表面的重构信息，通道中的目标数据在经过解复用后几乎被重建.

图7 探针接收的目标信号(黑色线条)和输出信号(带星号标记的蓝色线条)Fig.7 The target (black lines) and output signals received by probes (blue lines with asterisk markers)

图8 声学复用超表面解复用后恢复的信息Fig.8 Information was restored after demultiplexing by the acoustic multiplexed metasurface

3 结论

声螺旋模态的正交性使每个模态携带不同的轨道角动量，有效防止不同模态信号间的模态耦合和传输过程中不同通道间的串扰.同时，AOAM的振幅和相位相互独立，且是正交的自由度，这些不同的维度可以同时应用于声复用技术.这种基于声共振的信号解调结构在信号频率选择性方面也有显著优势.如果入射多路复用信号的频率与结构的谐振频率匹配，则声螺旋模式只能转换为平面波.相反，在其他频率范围内的入射载波不会干扰测量结果.这一优点进一步提高了通信系统的传输效率，减轻了数据后处理的负担.因此，无源声波共振解调结构固有的选频优势在实际应用中也有助于简化通信系统终端设备的复杂性.

综上所述，基于AOAM 信号的有效调制解调的声学复用超表面在声学通信中具有广阔的应用前景.未来的研究应深入研究声学超表面的工作原理，优化其结构和性能，并将其应用于更复杂的声学通信场景，同时通过结合深度学习等先进技术来优化方法，探索新的编码和解码方案，进一步提高对复杂环境的适应性，增强系统的性能和稳定性.有望在通信领域的水下声通信、声涡旋空间分离等方面提供新的思路和可能性.