数值天气预报模式的行星边界层方案热力预报变量选择

赵怡雪,周博闻

（中尺度灾害性天气教育部重点实验室，南京大学大气科学学院，南京，210023）

大气边界层是大气圈的重要组成部分，它包含地面以上约1 km 高度范围内的大气，是人类活动的主要场所，是大气圈与水圈、陆圈和生物圈进行能量和物质交换的主要介质，对天气和气候都具有重要影响［1］.大气边界层随日照规律，呈现显著的日变化特征：日间地表受太阳短波辐射升温，驱动大气边界层热对流的发生发展；夜间地表因长波冷却降温，边界层内则形成稳定层结.本文关注的是日间对流边界层（Convective Boundary Layer，CBL）中的热力过程，图1 的左半部展示了日间大气边界层的典型热力对流结构.如左图所示，在地表加热条件下，边界层内形成自下而上的热力环流，也称为非局地组织化热对流和热力相干结构［2］.这里的“非局地”特指热力环流在垂直方向贯穿整个边界层高度，其结构和湍流输送特征受边界层整体动热力强迫控制：依据边界层热力（主要为地表加热）和动力强迫（即边界层内的垂直风切变）的相对大小，非局地热对流常呈现单体和滚涡等不同组织形式［3-4］，对边界层内热量、动量和水汽的垂直输送起主导作用［5-6］.除此之外，边界层还内充斥着相对边界层高度而言尺度较小的湍涡，这些湍涡不直接受边界层整体动热力强迫的影响，因而具备更强的各向同性和水平均匀性特征.它们的湍流输送特征主要受局地梯度控制，因此也被称为局地湍涡［2］.

图1 左图为对流边界层典型热力结构示意图，实线代表边界层热泡，右图为虚位温Θv 和垂直湍流浮力通量-w----'--θ-v' 的垂直廓线示意图（zi 和BS分别代表边界层高度和地表浮力通量，改自赵昭和周博闻[11]）Fig.1 (left) Schematic of the classic convective structures in the convective boundary layer，solid lines outline a boundary layer thermal;(Right) the virtual potential temperature and buoyancy flux profiles (zi and BS represent the boundary layer depth and the surface buoyancy flux,respectively（Figure adapted from Zhao and Zhou[11])

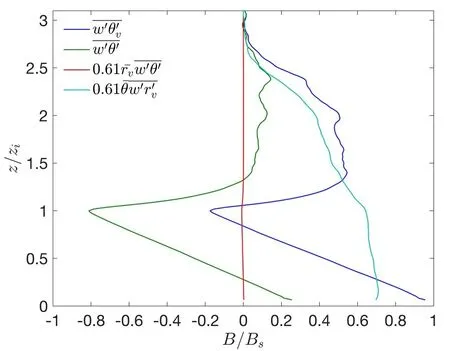
图2 海洋浅积云边界层中的垂直浮力通量及其组成分量的垂直廓线（数据源自对Barbados Oceanographic and Meteorological Experiment (BOMEX)个例的大涡模拟[13]）Fig.2 Vertical profiles of the vertical buoyancy flux and its constituents in a typical shallow cumulus-topped boundary layer (Data is obtained from large-eddy simulation of the Barbados Oceanographic and Meteorological Experiment (BOMEX)[13])

图3 六个具有不同波文比的理想对流边界层中的(a)感热通量和(b)浮力通量垂直廓线Fig.3 Vertical profiles of the (a) sensible heat fluxes and (b) buoyancy fluxes from 6 idealized CBL cases with different Bowen ratios

依据主导湍流过程的不同，对流边界层自下而上可分为近地层、混合层和夹卷层，边界层顶以上则统称为（不受边界层摩擦所束缚的）自由大气（图1）.各层中的主导物理过程决定了边界层虚位温θv(z)的廓线形态.近地层直接受陆面加热影响，呈现θv向上递减的超绝热廓线.由于受地面的限制，近地层中的湍流以尺度与离地高度相当的接地湍涡（Attached Eddy）为主［7］；在近地层之上的混合层中，非局地湍流旺盛发展，在强烈的湍流混合作用下，θv的垂直梯度接近于零；在与自由大气相邻的夹卷层中，非局地热对流在上升过程中受自由大气中稳定层结的抑制，在消耗完自身的垂直动量后又下沉至自身的中性层结高度.在下沉过程中夹带了部分自由大气中的高熵空气进入混合层（即垂直夹卷过程），造成了混合层上层（一般为z/zi＞0.4）的弱层结稳定性［8-10］.

图1 的右半边展示了经典对流边界层虚位温和浮力通量垂直廓线.这里选取虚位温作为边界层的热力变量，在非饱和的条件下（在对流边界层中，只在晨雾等极少数天气条件下，需要考虑饱和条件，这些情况不在本文的研究范围内），依据状态方程可得：

若将式（1）中的T通过无量纲压强π≡T/θ转换为位温θ，可得非饱和条件下的虚位温定义：

在数值天气预报模式和全球气候模式中，大气边界层的湍流混合过程由行星边界层（Planetary Boundary Layer，PBL）参数化方案（简称边界层方案）承担.确切地说，传统的边界层方案主要为模式提供边界层内的垂直湍流动量通量、热量通量、水汽通量，以及云水通量（主要用于处理边界层雾和层积云）；同时边界层方案也计算自由大气中由“干”湍流引起的垂直通量，即不涉及云的部分，云中湍流则由传统的积云方案（Cumulus Scheme）进行参数化.

1 理论

1.1 传统感热通量的修正因非局地热对流的存在，经典的湍流梯度扩散假设对边界层热通量并不适用，这一点从图1 可以看出.梯度扩散假设湍流热通量顺着位温梯度，从高位温向低位温传输，即：

其中，KH为湍流热交换系数.因为对流边界层受夹卷加热的作用，混合层中上半部分的位温廓线呈弱稳定态，依据式（7），感热通量在～0.4zi以上为负，代表热量下传，这显然与实际不符.不管是观测［15］、实验［20］还是数值模拟［21］都指出，在干边界层中，感热通量在～0.8zi以下皆为正，即热量上传，这主要是由非局地热对流引起的.因此，Ertel［22］，Priestley and Swinbank［23］和Deardorff［24］提出了针对非局地热通量的逆梯度修正项γcg，将式（7）修正为：

其中，γcg(z)定义在对流边界层内，且始终为正.对比式（7），式（8）右边新增的KHγcg保证了混合层中的正感热通量，因而被边界层方案广泛采用［10］.

为了确定γcg，Deardorff［8］提出基于诊 断方程的γcg表达式，并被后人不断改善［25-26］，Holtslag and Moeng［27］（简 称“HM91”）提出相对完善的推导，以下给出简要介绍.从水平均匀环境下的Bousinessq 近似预报方程开始：

其中，右边的四项依次代表垂直湍流混合项（T）、位温梯度生成项（M）、浮力项（B）和气压相关项（P）.需要注意的是，在HM91 的原文［27］中，浮力项的表达式为而非式（9）中的，这是因为HM91 仅考虑了干边界层湍流，浮力扰动等价于θ'.如前所述，干边界层假设也被几乎所有的前人工作所采用.

之后，基于一个大涡模拟的干边界层个例，HM91 给出了γcg推导过程中的关键假设，即湍流项和梯度项之间只相差一个常数，即：

而非更为普适的虚位温定义：

而后，HM91 又对式（9）中的气压项进行了如下参数化：

如前所述，式（16）中b，w*的选取需要针对湿边界层进行评估.

1.2 浮力通量这里探索前言中的提议.若采用干、湿环境皆可用且相似性更强的垂直浮力通量取代感热通量作为边界层的热力学预报变量，那么相应的浮力通量逆梯度输送项又是什么？为此，可以参照HM91 的推导，基于浮力通量的收支方程：

依次展开类似式（10）～（14）的推导.由于这里考虑的是浮力通量，在推导过程中将毫无疑问地摈弃式（11）的地表感热通量，而使用式（12）的浮力通量来定义w*.若将HM91 的工作看作边界层的干过程特例，则理应期待获得类似式（8）的浮力通量参数化，即：

及类似式（15）的逆梯度浮力通量修正项γcg，v，即：

式（19）中的w*也将毫无争议地采用式（12）的湿过程定义.但式（18）和式（19）是否具有足够的干湿普适性，是否存在不依赖于干湿过程的常数b，还有待于接下来的验证.

2 个例选择和模式设置

本文选择的湿边界层个例是浅积云经典算例Barbados Oceanographic and Meteorological Experiment（BOMEX）［30］，模拟典型的定常条件下的海上浅积云边界层.个例设置参照Siebesma et al［31］，关键实验参数如表1 所示，其中，(Ug，Vg)为地转风矢量，Vg恒为零为奥布霍夫长度，κ=0.41 为冯卡门常数为边界层整体稳定度（Bulk Stability）［6］，一般当时，边界层内的热对流组织方式为滚轴涡旋.在BOMEX 个例中，zi特指混合层厚度，即浮力通量到达最小值的高度.BOMEX 个例的初始位温廓线包含了近地500 m 的等熵层，500～1500 m 高度为湿对流条件不稳定层，1500 m 以上为绝对稳定层，初始风速廓线为地转风.个例设置中还加入了大尺度的沉降，结合平流及辐射冷却造成的位温倾向等环境变量，以实现定常态，具体设置详见Siebesma et al［31］的表1.

表1 BOMEX 个例和干对流边界层个例的关键实验参数设置Table 1 Key model parameters of the BOMEX case and the dry CBL case

为了对比干湿边界层中的非局地输送，本文还选取了一个具有和BOMEX 个例相似整体稳定度的干边界层（CBL）个例，关键实验参数见表1.CBL 个例的设置参照了Shin and Hong［32］，个例的初始位温条件为0～925 m 的等熵层，与925～1075 m 的覆盖逆温层以抑制边界层的增长，其上则为自由大气.初始风速廓线为地转风.

两个个例皆采用了大涡模拟，以尽可能真实地分辨湍流混合过程.BOMEX 个例的水平和垂直分辨率皆为10 m，采用(864，864，300)个网格点，模拟8.64 km×8.64 km×3 km 的三维空间.CBL 个例采用水平10 m，垂直4 m 的分辨率，采用(1008，1008，324)个网格点，模拟10.08 km×10.08 km×2 km 的三维空间.模式的水平方向采用双周期边界条件，地面采用预设通量作为边界条件（详见表1），模式顶则采用半滑动边界条件，并将模式顶部的1/4 高度设置为海绵层，以吸收上传的重力波.BOMEX 和CBL 个例分别经过4 h 和5 h 达到定常状态，而后又运行了3 h 以采集模式数据用于分析.

3 结果与讨论

图4 BOMEX 个例的(a)垂直感热通量和(b)垂直浮力通量收支（图注参照式(9)与式(17)）Fig.4 Vertical profiles of the (a) vertical sensible heat flux and (b) vertical buoyancy flux budget，legends follows Eqs.9 and 17

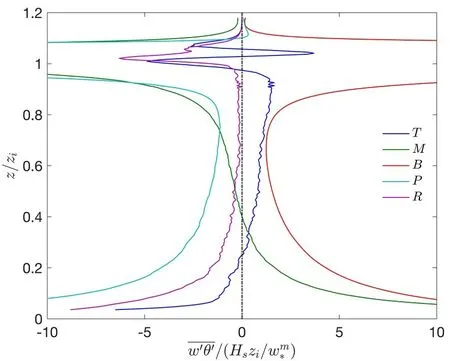
图5 如图4，CBL 个例的垂直感热通量收支Fig.5 As Fig.4,but for the CBL vertical sensible heat flux

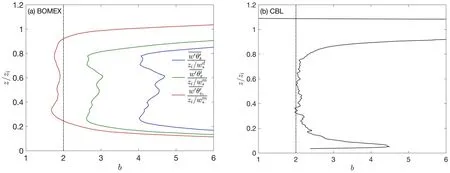
图6 (a) BOMEX 个例和(b) CBL 个例中的无量纲b 系数（参见式(10)）Fig.6 Vertical profiles of the dimensionless constant b in Eq.10 for (a) the BOMEX case and (b) the CBL case

考察式（13）中气压项的参数化.首先，将式（13）中Rotta 项的时间尺度τ替换为e/ε并引入系数CT，将式（13）变为可操作的参数化形式，即：

图7 (a) BOMEX 个例中的感热通量(黑线)和浮力通量(红线)收支中的气压项和(b) CBL 个例中的感热即浮力通量收支中的气压项Fig.7 Vertical profiles of the normalized pressure correlation term for (a) the sensible heat flux (black lines) and buoyancy flux (red lines) for the BOMEX case，and (b) the sensible heat/buoyance flux for the CBL case

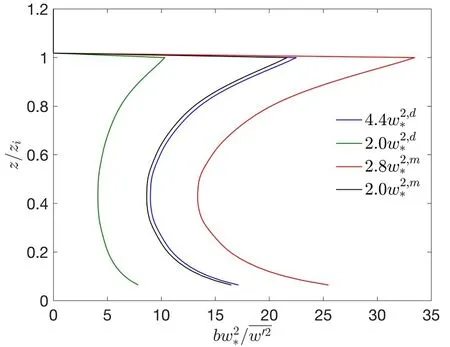
图8 BOMEX 个例中的标准化逆梯度修正项（式（16））及不同的b 系数Fig.8 Vertical profiles of the normalized countergradient correction term (Eq.16) with different b coefficients

4 结论与展望

（1）浮力通量收支的湍流和气压强迫项之差（即式（10））的系数b在干湿条件下皆为2（图6 和图8），而感热通量的b系数在湿边界层中要大于干边界层，采用浮力定义的自由对流速度会减小这一差距，但湿边界层中的b系数依旧要大于2，在BOMEX 个例中为2.8（见图6）.

（2）浮力通量的气压项参数化在干湿边界层中具有相同的Rotta 系数CT，因而可以采用同样的参数化方案，而感热通量的Rotta 系数在湿边界层中要大于干边界层（见图7）.而且基于浮力通量的气压参数化效果要略优于感热通量，具有更小的均方根误差.

由此可见，基于垂直浮力通量的边界层方案具备很好的干湿一致性，即方案关键系数不随湿度而改变，因此要优于传统的基于感热通量的边界层方案.基于上述认识，将虚位温作为边界层热力过程预报量，会比传统的位温预报具备更强的鲁棒性和更广的适用性.在程序方面，从位温到虚位温的修改，并不涉及任何对现有边界层方案的改变，只需在输入部分，利用式（2）将θ转化为θv，而后在输出部分，将计算所得，结合方案预报的水汽通量，利用式（4）转换回即可完成.这正是充分利用了浮力通量的干湿一致性，即完全可以认为传统的边界层方案就是针对浮力通量所设计的，只需输入正确的变量即θv就可以输出正确的参数化通量即我们已在WRF 模式中实现了这一变量转换，以后将展示改进效果.

致 谢感谢中国气象局上海台风研究所刘梦娟副研究员提供图3 的大涡模拟数据以及对赵怡雪的指导和帮助！