基于PINNs 算法的一维潜水流方程的渗流参数反演

舒 伟,孟胤全,邓 芳,蒋建国,吴吉春

（南京大学地球科学与工程学院，南京，210023）

渗流参数在地下水及石油工程领域扮演重要的角色，是描述和预测地下流体运动和能量传递的关键变量.在地下水管理、环境修复和油气田开发等领域，渗流参数如渗透系数的准确反演对于理解和预测地下水流及污染物运移至关重要.这些参数直接影响地下水模型的构建和精确性，进而对水资源评估、污染防治策略的制定与执行具有深远的影响［1］.因此，发展高效、准确的渗流参数反演技术是当前水文地质学研究的重要任务之一.

传统的渗流参数预测方法多基于地质调查、泵测试验及自然界中的水文地质现象，这些方法常常因为试验设计复杂、成本高昂、耗时长和在特殊地质条件下的适应性不足而受到诸多限制.此外，参数空间的非线性和模型的不确定性也给传统方法的应用带来了挑战［2］.

近年来，随着深度学习技术的飞速发展，越来越多的研究集中于利用神经网络方法进行水文地质参数的反演.例如，Huang et al［3］成功将基于编码器-解码器的卷积神经网络（Convolutional Neural Network，CNN）用于多孔介质中非均质多尺度的渗透率反演，同时降低了计算成本.Feng［4］将物理方程融入到生成对抗神经网络（Generative Adversarial Network，GAN）训练中，并成功用于反演储层孔隙度.此外，循环神经网络（Recurrent Neural Network，RNN）因其在序列数据处理中的优势，已被用于时间序列水文数据的分析，辅助渗流参数的动态反演［5］.

物理信息神经网络（Physics-Informed Neural Networks，PINNs）是一种结合了深度学习和物理定律的新型网络结构，它通过直接在神经网络损失函数中嵌入物理定律，能够让网络预测结果自然满足相应的物理规则.该方法由Raissi et al［6］在2019 年正式提出，开启了数据驱动和物理驱动模型融合的新篇章.PINNs 的核心思想在于将传统神经网络的优化目标，即减少预测与实际数据之间的差距，扩展到同时满足物理模型.在PINNs 中，网络不仅要学习数据特征，还要学习数据背后的物理法则.具体到渗流问题，这意味着网络预测的渗流参数需要同时满足观测数据和达西定律或其他相关流体力学方程，这样的网络结构允许PINNs 在数据稀缺的情况下也能做出物理上可靠的预测［7］.

在地下水领域，PINNs 的应用主要集中于参数估计和流场模拟等多方面.Almajid et al［8］利用PINNs 预测了多孔介质流体流动，表明PINNs 在融合物理信息和观测数据进行准确预测的有效性，此外还将其用于反演多相流参数并证明其优于没有物理信息的人工神经网络（Artificial Neural Network，ANN）.此外，Zhang et al［9］提出了一种求解有井地下水流方程的无标注数据深度学习方法GW-PINN，通过多个算例成功展示了其在预测地下水系统中水头的剧烈变化的能力.与传统的神经网络相比，PINNs 在渗流参数反演中表现出多方面的优势.首先，它通过内嵌物理定律，减少对大量训练数据的依赖，这在数据获取成本高昂或数据不易获得的地下水研究中尤为重要［10］.其次，PINNs 能够提供更加物理合理的解释，因为其预测结果必须符合物理定律，这降低了获得非物理解的风险［11］.最后，PINNs 在处理多物理场问题时表现出色，这使得它可以在处理复杂的地质和地下水系统时，有效整合和模拟多种物理过程［12］.

总体而言，PINNs 在地下水领域的应用还处于初步探索阶段，但已经显示了强大的潜力.目前PINNs 在潜水流问题中的研究极少，特别是对于潜水含水层的渗流参数反演问题的应用，潜水流方程的非线性也进一步加大了参数反演的难度.此外，在PINNs 的应用中对边界条件的处理多数采用的是软约束形式，而对硬约束形式的探究较少［13］.事实上，软硬约束各有其特别的优势，软约束可以理解为对模型的某些属性或参数采取柔和的限制，而不是硬性地限定它们，使它能保证模型具有足够的复杂性来拟合数据，同时避免过度拟合.硬约束的应用通常包括结构约束和参数范围约束.结构约束是指在某些情况下，使模型的某些部分具有特定的结构或模式，例如稀疏性或对称性.参数范围约束是指确保参数保持在预定义的范围内.硬约束为模型施加了严格的边界条件，使模型在这些条件下始终保持有效.例如，Sun et al［14］引入辅助函数 使PINNs 自动满足边界条件并进一步证实了PINNs 在硬约束下的适用性和准确性.然而，过多或过于严格的硬约束可能会限制模型的能力，使其无法学习复杂的模式.因此，选择适当的约束并平衡其强度是至关重要的.

综上，本文首次将PINNs 方法结合软硬约束设置来解决潜水含水层渗透系数反演问题，以一维稳态非均质潜水流以及非稳态均质潜水流（含溶质运移）的渗透系数反演为例，对比了不同问题中PINNs 软约束方法（PINNs-S）和硬约束方法（PINNs-H）反演渗透系数的表现，为后续研究PINNs 应用到更复杂的潜水含水层渗流参数反演问题中提供了参考.

1 算法和原理

1.1 控制方程及边界条件

1.1.1 潜水流控制方程对于计算域为Ω⊂Rn的潜水流动问题，其满足的控制方程为：

其中，∇为梯度算子；x=(x1，x2，…，xn)为空间坐标；K为渗透系数；h为含水层厚度，当隔水层水平时h=H，H为水头值；W为源汇项.

设边界条件为Dirichlet 边界条件，可以表示为：

根据达西定律，可得到渗流速度V(x)的表达式：

1.1.2 对流-弥散方程本文算例中溶质运移满足潜水含水层中对流-弥散方程：

其中，∇为梯度算子，x=(x1，x2，…，xi)为空间坐标，Di为弥散系数，C为溶质浓度，ui为流速.

相关的初始条件可以表示为：

相关的边界条件可以表示为：

其中，ΓD为研究区的边界，φ为已知函数，[0，T]为时间区间.

1.2 PINNs

1.2.1 PINNs 简介PINNs 是一种前沿的深度学习框架，它巧妙地融合了传统的数值模拟技术与现代的神经网络技术，同时它本质上是一种无网格技术，可以轻松处理不规则域问题［15］.通过在损失函数中加入物理约束，PINNs 能在数据驱动的学习过程中，同时考虑底层的物理规律.通常，深度学习模型主要依赖于大量的数据进行训练，但在许多实际应用中，数据可能是稀缺的.此时，通过利用已知的物理原理，PINNs 可为模型提供额外的指导.具体地，假设下面的微分方程描述了某个物理过程：

其中，u是需要预测的物理量（如温度、压强等），L是线性或非线性微分算子.PINNs 通过一个神经网 络uθ(x，t)来表示u，其中，θ是网络的待优化参数，(x，t)是网络输入.训练过程中，总损失函数不仅包括数据的误差，还加入了物理约束的误差：

其中，

PINNs 的网络结构如图1 所示，以(x，t)为坐标输入的全连接神经网络可近似表征物理解u，其网络输出为预测解，物理解u满足描述一定物理规律的偏微分方程（PDE）以及初始条件（IC）、边界条件（BC），则网络预测解也应该满足这些物理约束，此外预测解与物理解之间还存在误差，这些误差以一定的权重结合在一起构成总的损失函数，最后通过梯度下降方法最小化损失函数找到最优的神经网络参数

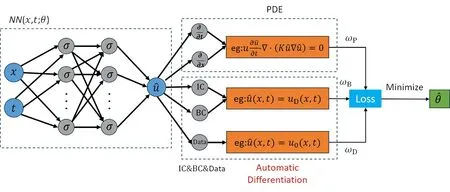
图1 PINNs 网络结构示意图Fig.1 Schematic diagram of the network structure of PINNs

1.2.2 自动微分自动微分（Automatic Differentiation，AD）［16］是计算机科学与数学交叉的一个领域，其目标是根据给定函数的计算过程自动高效地生成其导数或梯度.在深度学习的背景下，AD 成为模型训练的关键技术，因为大部分优化算法（如梯度下降［17-19］）都需要使用梯度信息.自动微分的核心思想基于链式法则进行微分.与符号微分和数值微分不同，AD 直接在函数的算法表示上操作，既不需要显式地给出数学表达式，也不依赖于数值逼近.假设有一个复合函数为则根据链式法则，它的导数是：

AD 就是自动地应用这一法则，将原函数分解为更简单的函数，并计算每一部分的导数.当优化一个神经网络时，最小损失函数需要计算网络参数的梯度.通过AD 可以有效地计算这些梯度，从而使用梯度下降方法来更新网络参数.

1.2.3 激活函数在深度学习中，激活函数起到了至关重要的作用，它决定了神经元的输出.激活函数为神经网络提供了非线性性质，使神经网络能够逼近非线性函数.没有激活函数，神经网络模型将退化为线性模型，无法解决复杂问题.常用的激活函数包括Sigmoid［20］，Tanh=和Leak y ReLU=max{ax，x}（a为任意常数）［24］等，本文训练神经网络采用近年来谷歌研究人员提出的新型激活函数Swish［25］，其表达式为Swish(x)=x*Sigmoid(x)，它兼顾了ReLU的简单性和Sigmoid的平滑性.

1.2.4 损失函数及模型评价指标深度学习中，损失函数（也称目标函数、代价函数或误差函数）是用于衡量模型预测值与真实数据之间的差异的关键组成部分，为优化算法提供了一个明确的指导，使模型能通过迭代不断改进其预测性能.本文训练神经网络模型采用的损失函数为均方误差函数.均方误差（Mean Squared Error，MSE）［26］是最常用的回归损失函数，它表示预测值与真实值之间的平方差的平均值.其数学表达式为：

本文采用的模型预测精度评价指标如下.

最大绝对误差（Maximum Absolute Error，MAE）：

平均绝对误差（Average Absolute Error，AAE）：

最大相对误差（Maximum Relative Error，MRE）：

平均相对误差（Average Relative Error，ARE）：

式（12）～（16）中，yi是实际观测值或真实标签是模型的预测值；i是样本的索引，通常对所有样本进行遍历；n是样本的总数，通常对所有样本进行求和.

本文的算例用于反演渗透系数场的神经网络的总损失函数包括基于一维潜水流方程的误差（MSEPDE）、基于定水头边界条件或定浓度边界条件的误差（MSEBC）、基于已知水头数据、溶质浓度数据或Darcy 流速数据的误差（MSEData），具体可表示如下.

总的损失函数：

其中，

式（18）～（20）中，ωP，ωB和ωData分别表示损失项MSEPDE，MSEBC和MSEData的权重，‖·‖2为 欧几里得范数，|τ|表示相应训练点的数量，τP和τB分别为研究区内部和边界上用于训练神经网络的物理点集合，τD为已知数据或模拟数据的观测点组成的集合分别表示神经网络预测的水头值和溶质浓度值表示神经网络预测的渗透系数值.通过梯度下降优化算法最小化总损失函数可以得到最优的神经网络参数，从而精确地预测渗透系数K.

1.3 硬约束和软约束

1.3.1 软约束深度学习模型由于其参数数量巨大和非线性特性，通常能够很好地拟合训练数据，但这也可能导致过拟合，使模型在新的数据上表现不佳.而软约束提供了一种平衡模型复杂性和训练数据拟合的方法，它对模型的某些属性采取弹性的限制，可以确保模型具有足够的复杂性来拟合数据，同时避免过度拟合.此外，由于约束是柔和的，模型还具有一定的灵活性，可以更好地适应新的数据.总之，软约束在深度学习中扮演着至关重要的角色，帮助研究人员在模型的表达能力和泛化能力之间找到合适的平衡.

1.3.2 硬约束在深度学习中，约束条件被广泛应用以确保模型的行为满足某些先验知识或特定条件.这些约束条件可以分为两类：软约束和硬约束.硬约束［27］是那些必须被严格遵守的条件.与软约束相比，硬约束为模型施加了严格的边界条件，使模型在这些条件下始终保持有效.硬约束可以形式化为：

其中，gi(w)是约束条件，且w是模型的参数；i表示索引，对应不同的约束条件.

硬约束的应用通常包括结构约束和参数范围约束.结构约束是指在某些情况下，使模型的某些部分具有特定的结构或模式，例如稀疏性或对称性.参数范围约束是指确保参数保持在预定义的范围内.例如，对于某些模型，可能希望权重矩阵的特征值保持在一个特定范围内以确保数值稳定性.其表达式为：

其中，λ(W)是权重矩阵的特征值.

和软约束相比，硬约束具有一些显著的优势，例如硬约束确保模型在所有情况下都满足给定的条件，这为模型提供了一个明确的操作框架，确保其不会超出预期的范围；另外，在面对潜在的对抗性攻击时可以提供额外的鲁棒性［28］，且由于模型的搜索空间被严格限制，它可能在某些情况下更快地找到满足约束条件的解；有时还可以提高模型的可解释性［29］，因为它们为模型的行为提供了明确的界限.

然而，值得注意的是，过多或过于严格的硬约束可能会限制模型的能力，使其无法学习复杂的模式.因此，在实践中，选择适当的约束并平衡其强度是至关重要的.总之，硬约束在深度学习中为模型提供了明确的操作边界，确保其行为始终满足预期.和软约束相比，硬约束提供了确定性和鲁棒性的优势，但需要谨慎使用以确保不限制模型的学习能力.

本文主要采用结构硬约束来使PINNs 自动满足边界条件，无需在总损失函数中添加额外的边界损失项，从而使网络更快地找到优化方向.基于此，假设研究区为[0，Lx]，东西边界为定水头边界条件，水头值分别为hL，h0.若采用硬约束方法，即同时满足两个定水头边界条件，则水头值h的表达式［29］可设为：

其中，NNθ(x，t)为神经网络的输出值，θ为神经网络参数，(x，t)为时空坐标，是神经网络的输入.

2 数值算例

2.1 算例简介本节将PINNs 软约束算法和硬约束算法应用于一维潜水流模型的渗透系数反演，通过参考解与PINNs 的预测解的对比，验证两种方法反演渗透系数的准确性并对比它们的预测效果，其中训练PINNs 所需的水头数据、溶质运移数据和Darcy 流速数据由COMSOL Multiphysics 数值模拟软件正向求解水流模型得到.算例中所有的PINNs 算法均采用Python 语言编写，计算采用深度学习框架Pytorch 1.1.

2.2 一维稳态非均质潜水流渗透系数的反演地下水一维稳态非均质潜水流模型满足式（1），其中方程右侧水头H对时间的偏导数为0，边界条件定为式（2），假设研究区为[0，1 ]，东、西为定水头边界条件，渗透系数K是空间的函数，设K=exp(sin(10x))，PINNs 硬约束算法中水头值h的表达式设为式（23）.网络训练迭代步数为20000，优化算法采用Adam 算法和L-BFGS-B 算法，即使用Adam 算法迭代至15000 步后，再通过LBFGS-B 进行优化，其他网络训练所需的超参数设置如表1 所示.表中NN表示神经网络结构（隐藏层神经元数×层数），τP和τB分别为研究区内部和边界上用于训练神经网络的物理点数，τD为已知水头数据和Darcy 流速数据的训练点数，lr为学习率.本例采用PINNs 求解的示意图见图2.

表1 一维稳态非均质潜水流PINNs 算例所采用的计算超参数Table 1 The computational hyperparameters used in the PINNs example of one-dimensional steady heterogeneous unconfined flow

图2 一维稳态潜水流模型PINNs 算法反演渗透系数的示意图Fig.2 A schematic representation of PINNs algorithm for the inverse estimation of hydraulic conductivity in the one-dimensional steady-state groundwater flow model

采用式（13）～（16）四种指标衡量模型预测神经网络性能，结果如图3 所示.

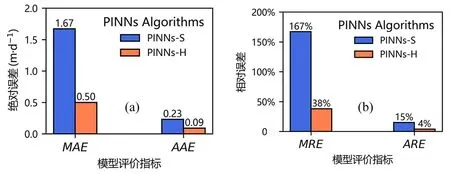
图3 一维稳态潜水流模型中两种PINNs 算法反演渗透系数的四种模型评价指标图Fig.3 Four model evaluation indices for inversion of permeability coefficients by two PINNs algorithms in the one-dimensional steady-state unconfined flow model

由图3 可以看出，PINNs-H 算法的表现要优于PINNs-S 算法，PINNs-H 算法的平均绝对误差为0.09，平均相对误差为4%，具有较高的反演精度.另外，从最大绝对误差（MAE）和最大相对误差（MRE）两项指标来看，PINNs-H 算法的MAE比PINNs-S 算法小1.17，而且前者的MRE比后者小129%，说明PINNs-H 算法网络预测的稳定性比PINNs-S 算法更好，这一点在图4 中也得到了直观验证.从图4 可以看到，在研究区域的后半段，两种PINNs 算法的反演效果均较好，但在前半段，PINNs-S 算法完全偏离了渗透系数的分布，PINNs-H 算法较好地学习到了参数分布，效果明显优于前者.此外，图5 对比了PINNs 软约束和硬约束算法的收敛速度，PINNs-H 算法的收敛速度整体上比PINNs-S 算法快，最终平均绝对误差也小于后者.硬约束算法的收敛速度较快可能是因为硬约束为模型施加严格的边界条件，从而减小了神经网络需要搜寻的函数空间，使得PINNs能更快地找到优化方向，与此同时也保证了模型良好的学习能力.

图4 一维稳态潜水流模型中PINNs 软约束和硬约束算法反演渗透系数结果图Fig.4 Results of permeability coefficient inversion by PINNs soft and hard constraint algorithms in the one-dimensional steady-state unconfined flow model

图5 一维稳态潜水流模型中两种PINNs 算法反演渗透系数的AAE 随迭代步数变化情况Fig.5 Variation of AAE with iteration steps in inversion of permeability coefficients by two PINNs algorithms in the one-dimensional steady-state unconfined flow model

2.3 一维非稳态均质潜水流渗透系数的反演地下水一维非稳态均质潜水流模型满足式（1），边界条件定为式（2），在此基础上加入溶质运移模型，该模型满足式（4），初始条件定为式（5），边界条件定为式（6）.假设研究区为[0，1 ]，东、西为定浓度边界条件，渗透系数设为K=1，反演中预测渗透系数的神经网络NN(K)采用的测试点数为50，取其预测的平均值作为PINNs 对均质渗透系数的预测值（即预测研究区内50 个坐标点处的渗透系数值，取其平均作为PINNs 最后的预测结果），PINNs 硬约束算法中水头值h的表达式和溶质浓度C的表达式均采用式（23）的形式.网络训练迭代步数为5000，优化算法采用Adam 算法，其他网络训练所需的超参数设置如表2 所示.表中τD为已知水头数据和溶质浓度数据的训练点数，其他超参数含义同表1.本例采用PINNs 求解的示意图如图6 所示.

表2 一维非稳态均质潜水流PINNs 算例所采用的计算超参数Table 2 The computational hyperparameters used in the PINNs example of one -dimensional unsteady homogeneous unconfined flow

图6 一维非稳态潜水流模型PINNs 算法反演渗透系数的示意图Fig.6 A schematic representation of PINNs algorithm for the inverse estimation of hydraulic conductivity in the one-dimensional unsteady-state groundwater flow model

采用式（13）～（16）四种指标衡量模型预测神经网络性能，结果如图7 所示.

图7 一维非稳态潜水流模型中两种PINNs 算法反演渗透系数结果的四种模型评价指标图Fig.7 Four model evaluation indices for results of permeability coefficient inversion by two PINNs algorithms in the one-dimensional unsteady-state unconfined flow model

与我们的预期不同，由图7 和图8 可以看出，PINNs-S 算法的表现优于PINNs-H，PINNs-S 算法的最大绝对误差为0.07，平均绝对误差为0.04，具有较高的反演精度.从图9 也可以直观地看到，PINNs-S 算法的收敛速度明显比PINNs-H算法更快.这是一个有些反直觉的结果，硬约束边界条件的嵌入减小了需要搜索的函数空间，但是PINNs 的精度和效率都在下降，推测其原因可能如下.PINNs 的损失函数最小化可以看作是一个多目标优化问题.在PINNs 的框架中，损失函数通常包含几个不同的组成部分，包括数据驱动的损失、物理驱动的损失、初始和边界条件的损失以及可能的其他正则化项，这些组成部分在优化时必须被同时考虑，因此PINNs 的训练过程需要在各个目标之间找到平衡.在多目标优化中，这些不同的目标往往是相互冲突的，即提高一个目标的性能可能会损害另一个目标的性能.在本节问题中，硬约束虽然自动满足了边界条件，但同时也可能限制了网络寻找到最优的折中方案.而软约束有效地平衡了模型复杂性和训练数据的拟合，此外它还具有一定的灵活性，可以更好地适应新的数据，所以最后取得了更好的预测效果.因此，要根据具体问题和实验效果来恰当选取硬约束和软约束，并不是所有硬约束边界条件嵌入的神经网络都更优越.

图8 一维非稳态潜水流模型中PINNs 软约束和硬约束算法反演渗透系数结果图Fig.8 Results of permeability coefficient inversion by PINNs soft and hard constraint algorithms in the one-dimensional unsteady-state unconfined flow model

图9 一维非稳态潜水流模型中两种PINNs 算法反演渗透系数的AAE 随迭代步数变化情况Fig.9 Variation of AAE with iteration steps in inversion of permeability coefficients by two PINNs algorithms in the one-dimensional unsteady-state unconfined flow model

3 结论

潜水流的数学模型是一种非线性偏微分方程，它的数值求解和方程参数反演都具有较大的挑战性.本文首次将结合物理规律和深度神经网络的PINNs 方法应用到潜水含水层渗透系数反演问题.以一维稳态非均质潜水流以及非稳态均质潜水流（含溶质运移）的渗透系数反演为例，对比了不同问题中PINNs 软约束方法（PINNs-S）和硬约束方法（PINNs-H）反演渗透系数的表现.计算结果表明，对于一维稳态非均质潜水流渗透系数的反演问题，PINNs-H 无论是计算精度还是计算效率，都显著优于PINNs-S.这是因为PINNs-H 将边界条件嵌入到水头函数的表达式中，其计算的水头值自动满足边界条件，训练神经网络时不需要计算边界点上的损失值，同时也减小了函数搜索空间.而将PINNs 用到非稳定态潜水流模型时，结果显示PINNs-S 的计算精度和收敛速度都优于PINNs-H.这说明对于复杂的非线性模型，软约束条件可能会更有效地平衡模型复杂性和训练数据的拟合，以避免过拟合的出现.因此，PINNs 硬约束算法和软约束算法各有优劣，在实际应用中应根据具体问题和实验效果来合理选择.

此外，还有一些问题需要进一步研究，如PINNs 软约束方法和硬约束方法具体在何种情况下或者何种问题设置中选用.为了处理工程实际问题，还需要将PINNs 应用到更复杂的高维或非稳态非均质潜水含水层的渗流参数反演问题中.