基于改进遗传算法的导弹稳定控制参数自寻优方法研究
2024-04-22高宏建陈霖周廷胡建兴苏小东汪阳生王文举
高宏建,陈霖周廷,胡建兴,苏小东,汪阳生,王文举
(1.贵州理工学院航空航天工程学院,贵州 贵阳 550025;2.贵州省无人机应急减灾信息化工程研究中心,贵州 贵阳 550003;3.中航贵州飞机有限责任公司,贵州 安顺 561000)
0 引言
导弹稳定控制参数的设计大多以经典控制理论为基础,首先采用小扰动线性化理论将时变非线性的导弹数学模型在弹体变化的若干个关键点(即特征点)上线性化为若干个参数分段定常的线性模型,然后针对这些定常线性模型,在保留足够的稳定裕度和性能的情况下设计控制系统。基于这种思想的导弹稳定控制参数的设计是建立在一定的“试凑”基础之上的,整个设计过程包含了多次循环迭代设计和校验过程[1]。
目前,工程设计中多采用以上先对特征点进行设计,再将设计结果应用于导弹稳定控制系统进行校验的迭代设计思路。但针对多个特征点,在无本质性差异的稳定裕度和时域性能等相同约束条件下,进行多次循环迭代设计和校验是这种设计方法的一个“弊端”。针对导弹控制参数的优化问题,管茂桥等[2]利用最速梯度下降法对攻角驾驶仪外回路的控制器参数进行了优化设计;王朝政等[3]用小生境遗传算法优化了靶弹爬升段弹道控制参数,通过罚函数的加入将待优化模型改造成无约束优化问题;徐帅等[4]采用随机鲁棒法优化了导弹姿态控制参数,该方法可以在一定程度上提高系统抑制弹体参数摄动的能力。但上述文献均未对优化算法收敛的快速性做出分析并给出改进措施。文献[5]为了减小导弹姿态控制对各级发动机合成摆角最大值的需求,用粒子群算法优化了姿态控制参数,通过将弹道特征与最优控制参数间的关系用多层神经网络拟合,虽然能够避免在线寻优过程耗时过长的问题,但这种解决办法是在参数寻优完成之后离线进行的,并未对寻优过程采取措施,优化过程耗时长的问题并未得到彻底解决。本文拟采用改进后的遗传算法实现对不同特征点控制器参数的自寻优设计,通过确定性因子的引入,不仅能够提高算法收敛于最优解的速度,还可将设计人员从多次循环反复设计和校验中解脱出来。
遗传算法(genetic algorithm,GA)借助“适者生存、不适应者被淘汰”的遗传学概念以及自然进化的思想,可以在全局范围内实现对复杂问题近似最优解的求解。遗传算法的随机性可以增加个体多样性,使其具备找到全局最优解的能力,但同时随机操作会以一定概率将父代最优个体排除在种群之外。本文针对遗传算法的随机性进行改进设计,通过引入确定性因子n,将父代适应度最高的前n个个体继承到子代,而对其他个体则仍以基本遗传算法进行随机遗传操作。
由Holland提出的Schema定理和由Goldberg给出的积木块假设是遗传算法的基础性理论支撑。模式定理表明,当一个特定“模式”适应度保持大于种群平均适应度时,可以保证此较优“模式”的个体按指数增长;而积木块假设则表明,在具有随机性的遗传算子作用下,算法能产生更高适应度值的“模式”,从而向更优的可行解方向收敛[6-7]。本文的侧重点在于改进基本遗传算法,通过引入确定性因子,在保留算法随机性的同时,使其具备一定程度的确定性,最终提高算法收敛于最优解的速度,并将改进后的算法应用在导弹稳定控制参数自寻优设计中,最后通过仿真验证算法的有效性。
1 基本遗传算法的实现步骤
基本遗传算法(simple genetic algorithm,SGA)的一般流程如图1所示[8]。
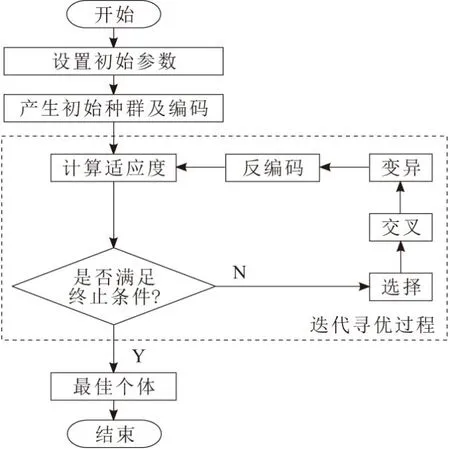
图1 基本遗传算法流程
a.种群初始化及编码。根据设定的种群大小,随机初始化产生初始种群,设定编码规则对每个个体进行编码,生成便于遗传操作的编码个体。为了解决不同的实际问题,提出了多种编码方法,包括二进制编码、整数编码[9]、浮点数编码、交叉编码、符号编码、多参数级联编码以及多染色体混合编码[10-11]等。
b.适应度计算及优化准则判断。针对每个个体计算适应度,并判断个体适应度是否符合进化终止条件,若符合则结束计算,同时给出近似最优解,否则跳转至步骤c。通常,适应度函数的设计要结合约束条件以及待解决的优化(最大值或最小值)问题来确定。需要指出的是,适应度函数设计的合理性,将在很大程度上影响问题优化的整体性能。
c.选择操作。依据父代个体适应度值以一定概率确定子代个体。常用的选择策略包括局部选择法、随机遍历抽样选择法、锦标赛选择法、轮盘赌选择法和截断选择法等。
d.交叉操作。按照交叉方法和一定的交叉概率,生成新个体。交叉操作相当于基因重组,可以采用二进制交叉中的单点交叉、多点交叉、循环交叉、顺序交叉、算数交叉[12]和交换启发式交叉[13]等方法。
e.变异操作。按照变异方法(包括二进制变异、实值变异、动态变异[14]和量子变异[14-16]等)和一定的变异概率,生成新个体,并返回至步骤b。
上述过程中,除种群大小、迭代次数、编码方式和适应度函数的设计等外,遗传操作(即选择、交叉、变异)中均含有随机性。本文是针对基本遗传算法中以概率遗传操作进行的一种改进设计。
2 基本遗传算法改进策略
基本遗传算法中的选择、交叉和变异操作,分别是在一定概率下确定的子代个体,子代个体存在随机性。因此,虽然群体中最优个体的适应度值最大,但在随机操作后,仍有可能导致群体中的最优个体随着进化过程的进行而被“筛选”掉,这样当代群体中的最优值将不能够遗传至下一代,进而影响算法向最优解的收敛速度。
针对上述问题,本文采取如下改进策略:

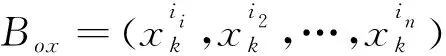
(1)
(2)
式中:i1,i2,…,in为进化前的n个最好个体索引标志。
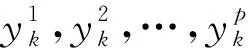
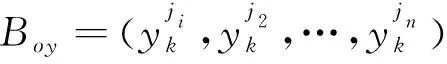
(3)
(4)
式中:j1,j2,…,jn为子代种群中的n个最差个体索引标志。
改进后的遗传算法流程如图2所示。

图2 改进后遗传算法流程
3 基于改进遗传算法的导弹稳定控制参数自寻优设计原理
3.1 被控对象模型
本文以弹体的俯仰平面为例展开介绍,弹体俯仰运动模型为
(5)
式中:a1、a2、a3、a4和a5为导弹动力系数;θ为弹道倾角;ϑ为俯仰角;α为攻角;Δδ为舵偏角。
3.2 稳定控制回路结构


图3 稳定控制回路结构
舵系统为控制系统的执行机构,其数学模型为
(6)
陀螺和加速度计为测量环节。陀螺用于测量弹体运动角速度,其数学模型为
(7)
加速度计用于测量弹体线加速度,其数学模型为
(8)
式中:T1为舵系统时间常数;T2和ξ2分别为陀螺时间常数和阻尼系数;T3和ξ3分别为加速度计时间常数和阻尼系数。
在设计之初,考虑到舵系统、陀螺和加速度计相对于弹体运动模型来说带宽较高,因此,可以将舵系统、陀螺和加速度计模型看作是直通环节,其数学模型可以在回路性能仿真验证时加以考虑。采用基于现代控制理论的极点配置设计控制器参数K1、K2、K3和K4,由于弹体为二阶环节,故闭环系统为三阶系统。这里确定期望特征多项式为三阶,即
f1(s)=p1s3+p2s2+p3s+p4
(9)
这样,设计出参数p1、p2、p3和p4后,即可通过极点配置法求解出K1、K2、K3和K4。现在的问题即可归结为:如何根据控制系统的主要性能指标要求(如上升时间、超调量以及稳定裕度等)来确定期望特征多项式的系数p1、p2、p3和p4,这将由改进遗传算法对其进行寻优求解。
3.3 基于改进遗传算法的导弹稳定控制参数自寻优设计
采用如图2所示的改进遗传算法流程进行导弹稳定控制参数的自寻优设计过程如下:
a.基本参数设置。种群大小设置为60,进化代数设置为200。
b.产生初始种群。通常,初始种群可以根据设计经验设定,或者在给定的参数范围内随机生成。为了验证算法的一般性,本文采取随机生成的方法产生初始种群。
c.编码方式及参数范围确定。采用二进制编码,变化范围为[amin,amax]的参数a和m位的二进制数b之间的关系可由下式确定,即
(10)
根据设计经验及参数精度要求,用长度为5的二进制编码串表示p1∈[0.03,0.20]和p2∈[1,2],采用长度为10的二进制编码串表示p3∈[30,120]和p4∈[20,115]。
d.遗传操作算子。本文采用的基本遗传操作为轮盘赌选择运算、2点交叉运算以及离散变异运算。
轮盘赌选择法是利用种群中每个个体xi的适应度值f(xi),计算得到每个个体的选择概率P(xi),最后利用累计概率L(xi)完成个体的选择操作[17]。
(11)
(12)
式中:N为种群大小。
基本遗传算法的交叉算子和变异算子为固定值,为了避免由此引起的寻优后期局部搜索能力差,算法出现早熟等现象,引入自适应调节交叉概率[18]Pc和变异概率[19]Pm的机制。
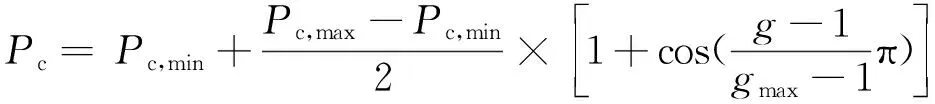
(13)
Pm=Pm,max-
(14)
式中:g为进化当前代数;gmax为进化最大代数;Pc,max为交叉概率最大值,取为0.9;Pc,min为交叉概率最小值,取为0.5;Pm,max为变异概率最大值,取为0.10;Pm,min为变异概率最小值,取为0.01。
本文对经过遗传操作后的子代种群,引入确定性因子n,将父代适应度最高的前n个(n的取值应视种群大小而定,但不能过大,一般取1或2即可,此处取n=1)个体保留至下一代。这样做的目的是增加一定程度的确定性,确保父代中适应度最高的个体一定能够被保留下来,而不是以概率被保留下来,并且n≠1可以在一定程度上避免算法陷入局部最优。
e.适应度函数的设计。为衡量控制回路响应性能,导弹稳定控制参数的设计除了要考虑时域指标(包括过载上升时间、超调量、振荡次数等),还要选用频域的稳定裕度为评估准则(包括幅值裕度、相位裕度等)。因此,适应度函数的设计原则为:综合体现各项指标要求,并且考虑到各项指标的性质、量纲不统一等因素,从而将适应度函数设计为如下形式的多目标加权适应度函数,即
(15)
式中:m为性能指标个数;xi为待优化参数;p1、p2、p3和p4为影响的第i项实际性能;xi0为第i项性能指标要求;ωi为第i项性能的权重系数[20]。
考虑到导弹稳定控制回路各项性能指标量级不同,故ωi实际可设计为第i项性能指标的无量纲系数。
4 仿真验证及分析
以某型导弹为被控对象,首先针对特征点采用改进遗传算法完成对导弹稳定控制回路控制器参数的自寻优设计,然后将寻优结果应用于六自由度仿真模型,以验证寻优设计结果的正确性和可行性。
首先,针对特征点采用上述设计进行参数自寻优,寻优设计结果如图4和图5所示。由图4可知,各点回路幅裕度大于6 dB,相裕度大于50°;由图5各特征点的单位阶跃响应曲线可知,各点过载响应超调量均小于20%,上升时间均小于0.5 s。
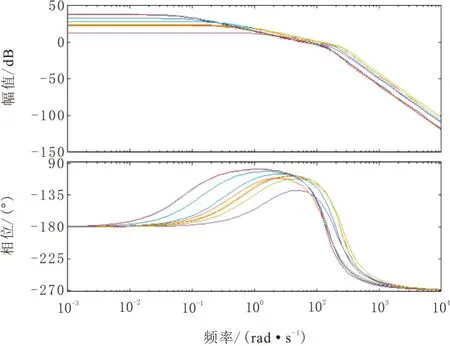
图4 各特征点的频域特性曲线

图5 各特征点的单位阶跃过载响应曲线
其次,将上述定点设计结果直接应用于六自由度仿真模型。以此型导弹的某条控制弹道为例,通过六自由度数字仿真检验控制弹道动态性能,仿真结果如图6 ~ 图9所示。由过载响应曲线可知,改进遗传算法自寻优设计的控制器与传统人工设计的控制性能相当;但由姿态角速度响应曲线、舵偏角响应曲线以及舵偏角速度响应曲线可知,改进遗传算法自寻优设计的控制器,其最大姿态角速度、最大舵偏角和最大舵偏角速度均小于传统人工设计结果,这将有利于工程实际应用。
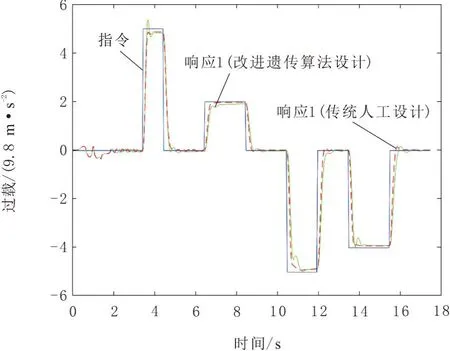
图6 过载响应曲线

图7 姿态角速度响应曲线

图8 舵偏角响应曲线

图9 舵偏角角速度响应曲线
最后,通过2个特征点仿真案例来分析本文改进措施的有效性。针对特征点1 和特征点2,设置进化代数为50,重复仿真20次。在不引入确定性因子的情况下,特征点1一次仿真最优适应度收敛曲线如图10所示,引入确定性因子后的一次仿真最优适应度收敛曲线如图11所示。特征点2引入确定性因子前后的一次仿真最优适应度收敛曲线如图12和图13所示。
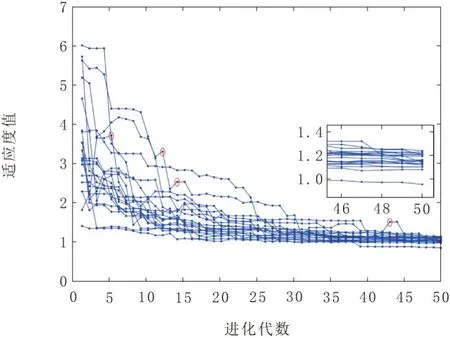
图10 特征点1改进前最优适应度收敛曲线

图11 特征点1改进后最优适应度收敛曲线
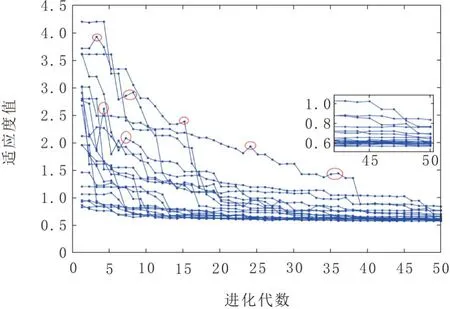
图12 特征点2改进前最优适应度收敛曲线

图13 特征点2改进后最优适应度收敛曲线
特征点1在不引入确定性因子的情况下,图10中,随着进化代数的增加,部分最优适应度曲线有起伏现象(如图中由圆圈所标示的几个点处),这表明遗传算子的随机操作将父代最优个体过滤掉了,且第50代最优适应度的最小值为0.956 9,最大值为1.241 3,均值为1.153 9,标准差为0.004 1。
特征点1采取改进措施后的图11中,每条最优适应度曲线均为单调递减,不存在起伏现象,表明由于确定性因子的存在,父代最优个体被保留下来,且第50代最优适应度的最小值为0.773 0,最大值为0.974 5,均值为0.880 6,标准差为0.003 2,均优于改进前。
特征点2引入确定性因子前后的一次仿真最优适应度收敛情况与特征点1类似,具体对比结果如表1所示。由表1可知,采取改进措施后,第50代最优适应度的最小值、最大值、均值和标准差均小于改进前,这表明采取改进措施后,算法向最优解收敛的速度得到了一定程度的提高。
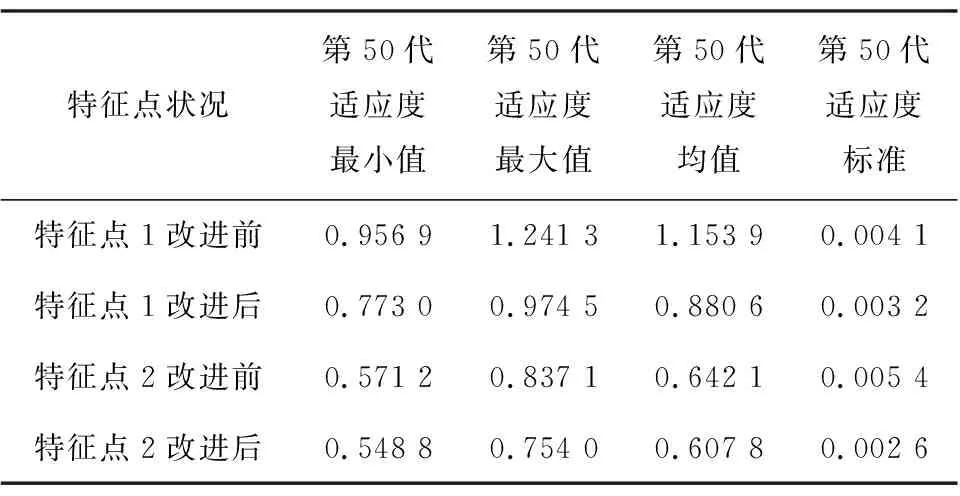
表1 引入确定性因子前后2个特征点终代最优适应度对比
5 结束语
针对目前导弹稳定控制参数设计中依赖设计师的工程设计经验、有可能无法在全局范围内获得组合优化的控制器参数问题,本文提出一种基于改进遗传算法的导弹稳定控制参数自寻优设计方法。针对遗传算法的随机性进行改进设计,通过确定性因子n的引入,将父代适应度最高的前n个个体保留至下一代,而不是以概率被保留下来,在保留随机性的同时,增加了一定程度的确定性。将改进后的遗传算法应用于某型导弹稳定控制回路的参数自寻优设计中,六自由度仿真结果表明控制效果良好,验证了改进措施的有效性。本文为实现导弹稳定控制参数的自动化设计提供依据,具有一定的工程实用价值。
本文引入确定性因子的改进措施,虽然能使算法具有一定确定性,但这种确定性本质上来说是相对于初代最优个体来说的,亦即算法的收敛是在初代最优个体基础之上,向全局最优解快速单调收敛的。因此,初始种群的生成将对算法最终的收敛值产生很大影响。对于此问题,可以通过先验知识来初步确定初始种群,也可以利用现代进化算法产生初始种群。另外,本文仅研究了确定性因子对基本遗传算法收敛速度的影响,尚未将其应用于其他形式的遗传算法。下一步将考虑确定性因子对其他形式遗传算法的有效性,以期使算法具有更快的收敛速度,达到更好的寻优效果。
