融合新旧产品退化信息的可靠性建模研究

2024-04-22唐家银王劲博刘新玲

机械与电子 2024年4期

吴怡,唐家银,王劲博,刘新玲

(西南交通大学数学学院,四川成都 611756)

0 引言

许多系统、产品和材料在失效之前都呈现老化、磨损或退化等特征,而监测性退化测量数据可以提供产品的退化衰减信息,对于该类数据的统计分析可以有效提高产品可靠性评估。在实际的退化测试和分析中,由于产品在制作过程中残留的杂质或是制作工艺本身的缺陷,一些产品的退化路径总是表现为2阶段模式[1-2]。如文献[3]中锂离子电池、发光二极管(LED)、等离子体显示面板(PDP)和真空荧光显示器(VFD)等系统都具有2阶段退化特征。运用变点线性回归模型对2阶段退化产品数据进行贝叶斯分析,得到产品性能退化量的变化趋势和突变点的精确估计,有效提高了该类产品的可靠性评估,有利于厂家制定合理的维修或销售策略。

关于变点线性回归的研究及应用受到国内外广泛关注[4-6]。目前,变点线性回归模型的贝叶斯估计方法是利用产品退化数据拟合得到产品退化路径重要方法之一,但大部分学者在利用变点线性回归模型分析产品退化路径时,总是将变点看作一个定值,而在实际应用中,退化变点往往具有随机性。

目前,对于小样本数据下的产品可靠性评估多数是从已知模型下提高参数估计精度入手,而贝叶斯可以融合多种信息,可以更有效地估计模型参数。为提高小样本非线性下的性能退化产品可靠性评估准确性,冯海林等[7]提出一种融合性能退化数据与寿命数据的可靠性评估方法;柯贤朝[8]利用相似产品信息和新产品信息,得到产品可靠性的融合后验,并在此基础上进行可靠性推断;Lu等[9]提出了一种基于多尺度超谐波特征偏转形状贝叶斯融合的阶梯转子裂纹定位方法;唐莉等[10]采用贝叶斯理论构建多个信息源数据融合的贝叶斯可靠性评估模型,解决小子样高可靠性长寿命产品的可靠性评估,提高可靠性评估的精准度。

本文采用贝叶斯方法融合2阶段退化新旧产品第1阶段退化数据信息,利用变点思想和变系数分段回归模型建立了变系数分段退化可靠性评估模型,完成了对新产品截尾数据的可靠性评估。

1 变系数分段线性回归模型

1.1 模型假设

模型假设具体如下:

a.基于新产品的失效机理,可以利用相同或相似类型产品的退化数据分析新型产品退化路径。二者退化量分布和参数估计量分布相同。

b.新产品原型可在一定试验规范的实际工况下进行测试,试验期间退化信号呈现多级退化模式。

c.具有随机参数的线性模型可以用来表征各阶段退化信号的变化,一些非线性模型也可以转化为线性模型。

d.对新产品样品的退化试验已经进行了一段时间,并获得了测量的退化数据的部分集合,即第1阶段退化数据。

1.2 变系数分段回归模型

变点线性回归模型可以写为

yij=

(1)

式中:yij为第i个样本的第j次观测值;tij为第i个样本的第j次观测时刻;n为样本总数;m为每个样本的观测次数;τi为该产品在第i组样本下的变点;ai0、ai1、bi0、bi1为第i个样本回归模型的待估参数;εij～N(0,σ2)。

也可以等价写为

yij=ai0+ai1tij+ai2(tij-τi)++εij

(2)

式中:(tij-τi)+=(tij-τi)·I(tij>τi)。显然有bi0=ai0+ai1τi,bi1=ai1+ai2。

2 参数估计

2.1 基于泰勒展开式的最小二乘法

利用最小二乘法估计回归模型(1)的系数和变点,相当于最小化式(3),即

(3)

(4)

再将式(4)代入式(3)得到

(5)

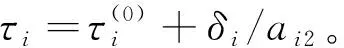
2.2 遗传算法求解参数值并拟合退化量分布

将极小化式(5)看作是多参数函数优化问题,这种问题通常可以通过遗传算法得到未知参数的估计[12-13],具体步骤如下所述:

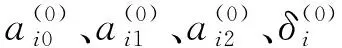
b.将二进制种群解码分别得到4个参数的十进制种群。把残差和函数式(5)作为适应度函数,分别将参数代入式(5),选择一定数目的更优个体进入下一步,称为轮盘选择。

c.在轮盘选择后的二进制种群中,以事先设置的交叉、变异概率进行个体间相互交叉和个体变异,最后得到新的二进制遗传种群。

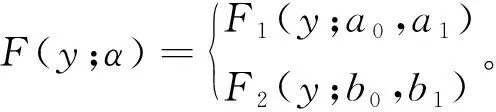
3 变系数分段退化可靠性评估模型

3.1 贝叶斯公式融合新旧产品退化信息

(6)

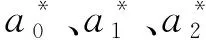
(7)

(8)

3.2 变点连续性建立阶段关系式

新产品在τi时,由变点的连续性得到

ai0+ai1·τi+εij=bi0+bi1·τi+εij

(9)

在式(9)两边同时取期望和方差,得到:

(10)

(11)

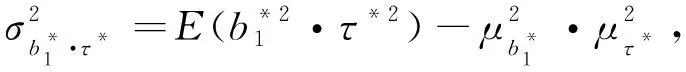
(12)

假设产品的失效阈值ηc为常值,那么可靠度函数为

(13)

4 算例分析

通过数值模拟,验证本文提出的基于变系数分段回归模型和变点思想的分段退化可靠性模型的有效性。使用蒙特卡罗方法(MC)产生相关的仿真样本数据:相似产品退化数据(100个样本,每个样本50次观测)、新产品截尾退化数据(100个样本,每个样本20次观测),假设回归模型系数估计量均独立服从高斯分布,参数取值如表1～表3所示。将仿真模拟结果与真值结果进行比对,最终分析判断模型的精准性。

表1 (相似产品)变量特征值与真值比较

基于相似产品仿真退化数据集,通过上述遗传算法得到未知参数ai0、ai1、ai2、δi的估计,再由极大似然估计得到变量的期望和方差以及第2阶段退化速率b1的相关特征量,如表1所示。通过贝叶斯方法融合第1阶段新旧产品退化信息,确定更新后各变量特征值,即新产品第1阶段各变量特征估计值,如表2所示。假设相似产品与新产品在第2阶段截距项相同,由变点处的连续性,以及式(10)和式(11)得到更新后第2阶段退化速率特征值,如表3所示。

表2 (新产品)第1阶段变量更新特征值与真值比较

表3 (新产品)第2阶段变量特征值与真值比较

图1～图7分别是相似产品的参数估计值散点图或频率直方图,表1是相似产品变量的特征估计值与真值的比较,从中可以看到各参数估计值均在期望附近波动,其特征值与真值差异很小,验证了参数估计方法的准确性。

图1 a0估计值散点图

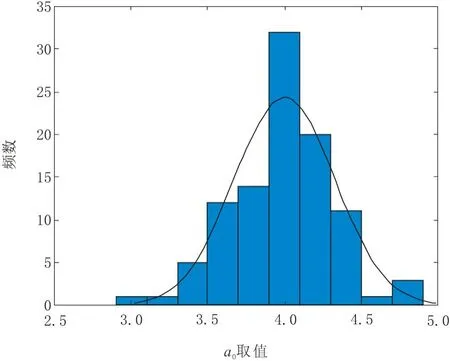
图2 a0估计值频数直方图

图3 a1估计值散点图

图4 a1估计值频数直方图

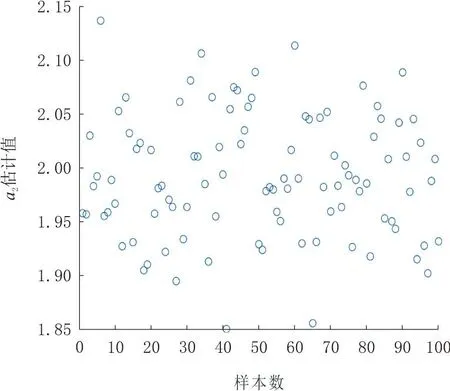
图5 a2估计值散点图

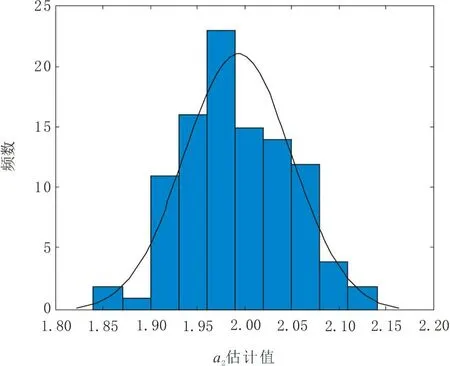
图6 a2估计值频数直方图

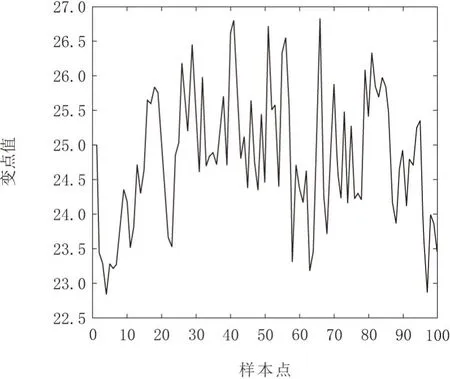
图7 τ估计值曲线

则新产品的退化量为

(14)

假设产品的失效阈值ηc为(常值),那么可靠度函数为

R(t)=

(15)

图8给出了给定阈值下相似产品和新产品的预测与实际可靠度函数曲线,从中看到新旧产品在第1阶段可靠度保持在100%不变,进入第2阶段后可靠度开始逐步递减,新产品的可靠性曲线呈现平缓递减趋势,基本上,在相同可靠度下,新产品的可靠寿命较大,符合实际背景。相似产品和新产品的预测可靠度函数曲线趋势基本相同, 对于新型产品的可靠度预测误差主要体现在第2阶段,总体预测误差较小,验证了模型的有效性。

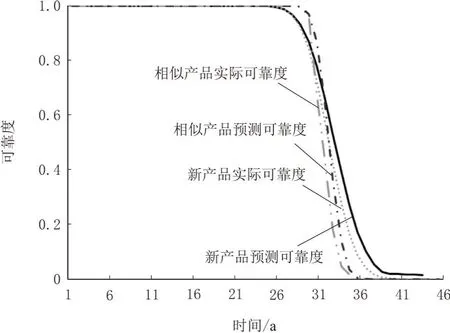
图8 新旧产品预测与实际可靠度函数曲线

文献[14]根据加速模型,在各温度应力下设定相应参数值,利用蒙特卡罗方法仿真各数据集,相应参数值如表4所示,本文模型与文献[14]模型下的可靠度函数曲线对比如图9所示。

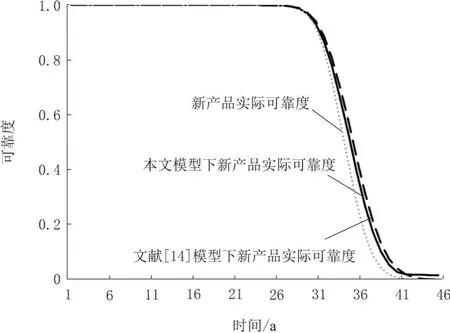
图9 本文模型与文献[14]模型下的可靠度函数曲线对比

表4 加速应力下分布参数设定值

文献[14]提出了一种融合内场加速退化试验与外场退化信息的可靠性评估方法,首先构建加速应力下的退化模型,然后将各加速应力折算得到正常应力水平,构成参数先验分布数据样本,利用贝叶斯融合内外场数据信息获得分布参数的估计。而本模型完全建立于实际工况下数据(外场数据),节省了试验成本和时间。从图9可以看出,本文模型与加速试验下得到可靠度函数曲线趋势基本相同,本文模型下的可靠度更接近于实际可靠度。