Long-term operation optimization of circulating cooling water systems under fouling conditions

Jiarui Liang ,Yong Tian ,Shutong Yang ,Yong Wang ,Ruiqi Yin ,Yufei Wang ,*

1 School of Chemical Engineering and Environment,China University of Petroleum,Beijing,102249,China

2 CHN Energy Xinjiang Chemical Co.,LTD,Urumqi,830092,China

3 College of Mechanical and Transportation Engineering,China University of Petroleum,Beijing 102249,China

Keywords: Computer simulation Circulating water system Fouling Concentration cycle Optimization Variable frequency drive

ABSTRACT Fouling caused by excess metal ions in hard water can negatively impact the performance of the circulating cooling water system (CCWS) by depositing ions on the heat exchanger's surface.Currently,the operation optimization of CCWS often prioritizes short-term flow velocity optimization for minimizing power consumption,without considering fouling.However,low flow velocity promotes fouling.Therefore,it's crucial to balance fouling and energy/water conservation for optimal CCWS long-term operation.This study proposes a mixed-integer nonlinear programming (MINLP) model to achieve this goal.The model considers fouling in the pipeline,dynamic concentration cycle,and variable frequency drive to optimize the synergy between heat transfer,pressure drop,and fouling.By optimizing the concentration cycle of the CCWS,water conservation and fouling control can be achieved.The model can obtain the optimal operating parameters for different operation intervals,including the number of pumps,frequency,and valve local resistance coefficient.Sensitivity experiments on cycle and environmental temperature reveal that as the cycle increases,the marginal benefits of energy/water conservation decrease.In periods with minimal impact on fouling rate,energy/water conservation can be achieved by increasing the cycle while maintaining a low fouling rate.Overall,the proposed model has significant energy/water saving effects and can comprehensively optimize the CCWS through its incorporation of fouling and cycle optimization.

1.Introduction

Circulating cooling water systems(CCWS)are widely applied in industrial production as water treatment systems for cooling,heating and conveying.They are used to release industrial waste heat to the environment.Optimizing circulating water systems improves water utilization and reduces operating costs.Several studies have optimized individual components when designing circulating water systems,including pumps [1,2],cooling towers[3],heat transfer networks [4],or through air coolers [5],variable frequency drives (VFD) [6,7] for system optimization.The main optimization methods are the pinch method [8] and the mathematical programming method [9],etc.

Despite numerous experimental and simulation studies,predicting and preventing fouling is still an unsolved problem in engineering,resulting in huge economic losses and environmental damage[10].More than 90% heat exchangers in various industries are experiencing fouling [11].Circulating water contains a large number of mineral ions,such as calcium,magnesium,etc.,evaporation in the cooling tower makes the ions constantly concentrated.When the circulating water in the exchanger is heated,the solubility of minerals is reduced,previously dissolved in the fluid calcium carbonate began to precipitate,and deposited on the surface of the pipeline.Fouling of circulating water system includes (i)particle fouling,(ii) crystalline fouling,(iii) corrosion fouling,(iv)biofouling,etc [12].Fouling increases the thermal resistance between the fluid and the heated surface,decreasing the heat transfer performance.The inner diameter of the heat exchanger tube decreases continuously with the accumulation of fouling.The velocity of the heat exchanger tubes will increase,results in a rise of pressure drop under the same flow rate.

Kern and Seaton [13] first proposed that particle fouling at the wall consists of two processes,fouling formation and removal,and the net fouling rate is the difference between the fouling formation rate and the removal rate.Due to the general applicability of the Kern-Seaton model,many scholars have performed mathematical expressions of fouling deposition rate and removal rate to optimize the simulation of fouling.Fouling simulations were performed for plate heat exchangers [14] and enhanced tubes [15],etc.Several studies optimized the operation of cooling towers and pipe networks under fouling conditions,proposing models and optimization strategies[16-18].To solve the corrosion and fouling problems in cooling water systems,fouling inhibitors are used in CCWS including phosphates,polyphosphates,organophosphonates,etc[19].

Under the influence of fouling,many system parameters and heat transfer network performance will be changed,and such variation is often complex and non-linear,so the impact of fouling on the whole system requires comprehensive consideration.Ebert and Panchal [20] proposed the fouling threshold model to predict the fouling rate of pipes inside the heat exchanger.Ishiyama et al.[21] considered the heat exchanger fouling problem and aging problem to solve the optimal cleaning cycle.Rodriguez and Smith[22] optimized heat exchange network based on wall temperature and flow rate to mitigate fouling.Cremaschi and Wu [23] studied the effect of fouling on the thermal performance of condenser and water consumption of cooling tower system,and established the prediction model of fouling rate by experiment.Souza and Costa[24]applied the fouling rate model proposed by Cremaschi and Wu to the optimization of CCWS,arguing that the behavior of each cooler in the network depends on the operation of the other heat exchangers in the system.Tian et al.[25]optimized the method to reduce fouling by simultaneously optimizing the flow rate and cleaning schedule.Diaz-Bejarano et al.[26] established a thermohydraulic dynamic model in refinery heat exchangers to characterize and evaluate fouling.Most of the researches at this stage are limited to optimize mass flow rate of the system to mitigate fouling,but the optimal configuration and operation of CCWS under fouling condition has not been well studied.

Concentration cycle is a key parameter affecting fouling and water replenishing,which is the ratio of the concentration of dissolved substances in circulating water to the concentration in make-up water.The higher the cycle,the more efficient the circulating water system is in recycling water,but it also brings fouling and corrosion problem.Cycle reflects the trade-off between fouling and reserving water.The relationship between fouling rate,heat transfer,pressure drop,and concentration cycle is highly complex,with mutual interactions.Ion concentration,flow velocity,and temperature simultaneously influence fouling.Additionally,fouling reduces the actual inner diameter of pipelines,leading to increased flow velocity,pressure drop,and weakened heat transfer effectiveness.Temperature and flow velocity also impact pressure drop and heat transfer,and variations in heat transfer effectiveness further affect the fouling rate.During the operation of CCWS,the cycle is monitored and adjusted regularly to save water while inhibiting fouling.Most of the current researches are to increase the cycle by adding fouling inhibitors [19],or study the effect of physical water treatment to inhibit fouling under high concentration cycle operation [27].In contrast,static cycle is often used in system optimization [28],with less consideration given to optimizing dynamic cycle in long-term operations.Determining the optimal value of cycle in long-run operation has multiple meanings of fouling inhibition,water saving and energy saving.

Current research mainly optimizes the design of the heat exchange network,pumps,piping and other parts of the CCWS,with less consideration of fouling and cycle on the overall operation optimization,omitting the interaction between fouling,heat transfer and pressure drop.Therefore,based on previous study [6]on system optimization using VFDs,a MINLP model using genetical algorithm (GA) was proposed to solve the optimal cycle,pump system configuration(pump on/off and VFD),and valve opening of CCWS.The synergy of the system,including cooling tower,fouling,heat transfer and fluid transportation,are considered to optimize the configuration of pump and piping system.And the impacts of cycle on heat exchanger fouling under long-term operation are evaluated.In order to verify the robustness of the model,sensitivity analysis was performed on nine sets of static cycle and three sets of ambient temperatures to determine the optimal static cycle for long-term operation and to investigate the overall effect of fouling on the configuration of the system at varying ambient temperatures.

2.Problem Statement and Mathematical Formulation

2.1.Problem description

Fig.1 shows (a) the structure diagram of the CCWS and (b) the program block diagram.The problem is the optimization of the operation of a CCWS,where the information on the heat flow,the inlet water temperature of the heat exchanger is available,but the outlet water temperature is unknown,which is solved by the number of Transfer Units (NTU) method.In the long-term operation,the water temperature fluctuates with the seasons,from January to December,taking one month as an interval.The pumps and heat exchangers are all connected in parallel (Fig.1(a)).The pumps contain constant speed pumps (CSPs) without VFDs installed and variable speed pumps (VSPs) with VFDs.The main pipeline and all branches each have a valve to regulate the flow together with CSPs and VSPs.In the fouling part,the ion concentration of the make-up water is the initial ion concentration,and the ion concentration in different operating cycles is adjusted by the cycle.Only the fouling of the heat exchanger tube process is considered(the heat flow goes through the shell side).The cooling tower reduces the circulating water to the inlet water temperature of the heat exchanger by evaporation.The blowdown and make-up water are calculated based on the cycle.

Fig.1.(a) Framework and (b) flowchart of the proposed circulating water system framework.

Genetic algorithm is used to find the optimal parameters.The independent variables in the system,such as pipeline resistance coefficient,whether to install VFD,VFD speed ratio,etc.,are combined into an array called DNA,while several individuals are combined into a population,and each population is called a generation,and by estimating the adaptation value of each individual in the generation,according to the evolutionary rule of“survival of the fittest”,the individual near the optimal solution in the generation is selected,and new generations are generated by DNA “crossover” and “mutation,” and then the above operation is carried out continuously,and the optimal index is selected by multiple iterations.The calculation can be divided into four main steps.In the first step,GA initializes the variables including the cycle,number of VSPs and CSPs,speed ratio of the VSPs,and the resistance coefficients of the main and branch valve,along with the GA population.In the second step,the characteristics curve of the pump and pipeline are calculated based on the initialized pump and VFD quantity,and valve resistance coefficients.The characteristics curve of the pump and pipeline are then combined to solve the flow rate of the first operation period(e.g.,month,day,hour,etc.,in this study,it is a month).In the third step,fouling and heat flow exchange are calculated,and the completion of the cooling task of the first interval is judged based on the heat exchange results.In the fourth step,the results of the next interval are calculated successively until all the intervals are completed.The objective function is then calculated,and if the heat exchange of a certain heat exchanger fails to meet the requirement in a specific interval,the linear penalty function is used to increase the cost of the objective function.It adds a fixed cost to the objective function if a heat exchanger does not meet the heat transfer requirements in a given month,with the total penalty cost proportional to the number of heat exchangers not met in all months.GA is iterated continuously to obtain the optimal solution.

2.2.Fluid transportation model

In the fluid transportation part,V(m3∙s-1)is the total flow rate of the CCWS,ΔP(kPa)is the total pressure drop of the system,the two parameters are obtained by coupling the characteristic curves of the pump and the pipeline,the total pressure drop of the pipeline can be expressed by Eq.(1),where Δpp(kPa)is the pressure drop of the main line,Δpex(kPa) is the pressure drop of the ith heat exchanger,Δpbranch(kPa) is the pressure drop of branch valve.Ht(m) is the height of the cooling tower and He(m) is the heat exchanger maximum height.The characteristic curve of the pipeline can be expressed by Eq.(2),ρ (kg∙m-3) is the density of circulating water,and g (kg∙m∙s-2) is gravitational acceleration,and both are constants.

For a pump,its characteristic curve can be represented by Eq.(3),where Ajand Bjare constants of pump j.

Its efficiency ηjcan be expressed by Eq.(4),where Cj,Dj,Ej,Fjare constants in relation to the properties of the pump j.

According to the law of proportion,the speed of the pump is changed,and the characteristic curve becomes an Eq.(5),kjis the speed ratio of the VFD,and all the kjof variable speed pump is set equal.

The characteristic curve of the paralleling pumps can be expressed as Eq.(6),where ωjis the 0-1 variable,indicating the opening and closing of pump j.The total flow rate can also be written as the sum of the flow rates provided by all pumps,or the sum of the flow rates of all the branches where the heat exchangers are located.

Since all pumps are connected in parallel,the head of the pumps are equal.ΔPp,ΔPexand ΔPbranchare calculated by Eqs.(7)-(9).λ is the coefficient of friction,and l (m) is the length of the main pipe,and d (m) is the inner diameter of the main pipe.The subscript ex represents heat exchanger,where ξmainand ξ are the local resistance coefficient of the main pipeline and the branch.

The flow rate in the heat exchanger pipe can be written into Eq.(10) according to the flow balance.

The flow rate in the main pipe can be written as Eq.(11).

The flow rate of the circulating water in the branch where the heat exchanger is located ubranch(m∙s-1) can be expressed as Eq.(12),where dbranch(m)is the inner diameter of the pipe where the heat exchanger is located.

The coefficient of friction can be calculated by Eq.(13),where e(m) is the roughness of the pipe.

The flow of the main line passes through the parallel heat exchanger,its flow distribution can be expressed by Eq.(14),where Vpercent(n,i)(dimensionless)is the proportion of the flow rate of the heat exchanger to the total flow rate of all heat exchangers.

The flow distribution of branch i1and branch i2is derived by deriving the same pressure drop,and the pressure drop of branch i1and branch i2are same,expressed by Eq.(15).

The proportion of the flow rate of the branch of the heat exchanger i is shown is Eq.(16).

2.3.Cooler model

Each heat exchanger undertakes a fixed heat transfer task,using heat to constrain the flow rate of circulating water,and Eq.(17) is used to describe the heat load of the heat exchanger to meet the heat exchange requirements.

The heat load required for the cooling of the hot stream can be calculated by Eq.(18),where cph(J∙kg-1∙K-1)is a constant,for the constant pressure heat capacity of hot stream,Mh(kg∙s-1)refers to the mass flow of hot stream,and T1is the inlet temperature of hot stream,and T2is the temperature of hot stream after cooling.

The heat load Q of circulating water can be calculated by the NTU method,which has three important parameters,the ratio of the heat capacity flow rate of the hot and cold fluid R,NTU and ε.where R is the ratio of the smaller fluid heat capacity flow rate to the larger heat capacity flow rate of the heat exchanger i in subperiod n,and R <1,which can be calculated by Eq.(19).

NTU is the number of heat transfer units,which can be calculated by Eq.(20),where K is the convective heat transfer coefficient outside the heat exchanger tube,which can be calculated by Eq.(21),where Rf (W∙m-2∙K-1) is fouling thermal resistance.The convective heat transfer coefficient in the tube is related to the flow rate of the fluid in the tube,which can be calculated with Eq.(22).A(m2) is the heat exchange area of the heat exchanger,which is determined by the heat exchanger itself.Circulating water takes the tube side,and the hot stream takes the shell side.

In Eq.(23) ε is the heat transfer efficiency,which can also be expressed by Eq.(24),and the ε is the ratio of the heat load Q to the theoretical maximum heat transfer Qmax,indicating the heat transfer efficiency of the heat exchanger.

The theoretical maximum heat transfer Qmax(W) can be calculated by Eq.(25).

Combining Eqs.(24)and(25)yields the heat load Q of the heat exchanger i.

2.4.Cooling tower formulation

The fouling of heat exchangers depends largely on the quality of circulating water.With the continuous evaporation of water in the cooling tower,the ion concentration in the water rises,so it is required to keep the water in the system stable by replenishing and discharging the water.The concentration cycle πcis an essential parameter in cooling tower and fouling models,which reflects the ratio of the ion concentration in the circulating water to that in the supplemental water,expressed in Eq.(27).

The flow rate of the makeup water is calculated in Eq.(28)[29].

The flow rate of the blowdown water is show in Eq.(29).

To ensure that the total amount of circulating water is equal,the flow rate of makeup water should be equal to the sum of the blowdown and evaporation.

The amount of water lost by evaporation from the cooling tower can be expressed by Eq.(30).Where the inlet water temperature of the cooling tower is then equal to the outlet water temperature of the heat exchanger,and the outlet water temperature of the cooling tower is equal to the inlet water temperature of the heat exchanger.

2.5.Fouling model

For the fouling model of cooling water,in this work,the model proposed by Ref.[23] is applied.In this model,the fouling rate of cooling water can be described by a competition relation between fouling formation rate and fouling removal rate.Fouling rate is related to fluid velocity,activation energy,Reynoldsnumber,Schmidt number andthe solubilityof calcium carbonate,as showninEq.(31).It isnoted that the above-mentioned physical properties of cooling water have great impacts on the fouling rate,and it is assumed that the impacts of other physical properties such as pH and silica content are ignored.

where,(dRf/dt)(m2∙K∙W-1∙s-1)is the fouling rate of cooling water,φdis the precipitation rate of calcium carbonate,φris the removal rate of calcium carbonate,and ρf(kg∙m-3)and λf(W∙m-1∙K-1)are the density and conduction coefficients of fouling.

The precipitation rate of calcium carbonate φdcan be calculated through Eq.(32).

where,kspis the product of calcium carbonate solubility,[Ca2+]andare the concentration of calcium ion and carbonate,kris the nondimensional coefficient of precipitation rate,and kdis nondimensional transfer coefficient.

krand kdcan be calculated through Eq.(33) and Eq.(34).

where,Rg(kJ∙kmol-1∙K-1) is universal gas constant,T (K) is temperature,subscript W means wall,Re is Reynolds number,and Sc is Schmidt number.

Schmidt number can be calculated through Eq.(35).

where,μw(Pa∙s) is the dynamic viscosity of water,D is molecular diffusion coefficient,and D can be calculated through Eq.(37).The wall temperature Tw(K)after fouling correction is calculated by Eq.(36).

Removal rate is defined as Eq.(38):

where,ψ is the model parameter of fouling rate model.

When the fouling rate dRf/dt of a sub-period is calculated out,the fouling heat transfer resistance of the sub-period can be calculated by fouling rate and the fouling heat transfer resistance of the previous sub-period,as shown in Eq.(39).In the equation,Rf(t+1) is the average value of fouling resistance.Based on fouling heat transfer resistance,the thickness of fouling layer can be calculated out,as shown in Eq.(40).

From the fouling rate model,it can be seen that cooling water velocity has significant impact on fouling rate.Meanwhile,the existence of fouling layer will reduce flow area in the tube,leading to an increase in velocity.Such increase in velocity will then affect the fouling rate.In addition,from the fouling rate model,fouling rate has a close relation with wall temperature,and wall temperature is determined by the operation condition of coolers (heat transfer coefficient and fluid temperature).The existence of fouling layer will reduce heat transfer coefficient,indicating that the wall temperature can be affected by fouling.Then fouling rate will be changed according to the change in wall temperature.

The tube inner diameter of the heat exchanger after fouling is corrected to Eq.(41),and then the flow rate of circulating water in the heat exchanger is corrected to Eq.(42) The equations Vpercent,and Δpexfor fluid flow are corrected by considering the fouling flow rate and the tube inner diameter.

2.6.Cost function

The objective function of the system is to minimize the total cost,and the total cost is the sum of the costs of the various parts,and,as shown in Eq.(43).

The pump operation cost VFD investment cost can be expressed in Eq.(44).In the pump total cost equation,Pe(USD∙kW∙h-1)is the price of electricity per kilowatt-hour.nVFDis the numbers of VFDs,and PVFD(USD)is the capital cost of one VFD,and i is an annualized interest rate,and nyearis the year in which the appliance is simulated to run,and npumpis the number of pumps.The price of installing a VFD on a pump is related to the rated power of the pump,so the capital cost of installing the VFD can be expressed by Eq.(45),where Prated(kW)is the rated power of the pump,and Punit(USD∙kW∙h-1) is the cost of VFD per unit rated power pump.

The operating costs of the cooling tower mainly include the operating costs for fresh water makeup and blowdown water treatment [30].Fan operating costs are ignored as they are not significantly affected by fouling.

3.Case Study

To verify the effectiveness and accuracy of the model,a case of a CCWS was simulated and analyzed in this study.The simulation was conducted under three different scenarios:fouling,where the cycle was set as the optimization variable;Cycle 5,where the cycle was fixed at 5;and non-fouling,where fouling was not considered.The simulation lasted for three years,and the inlet temperature of the cyclic water varied from 18°C to 30°C (291.15-303.15 K) according to the month,with the lowest temperature of 18°C(291.15 K)in winter and the highest temperature of 30°C(303.15 K)in summer.The economic performance,fouling situation,and system operation of fouling vs.non-fouling and fouling vs.Cycle 5 were compared and analyzed,and a total of 12 sensitivity analyses were conducted,including nine sets of cycle (from 2 to 10) and three sets of temperatures.

The three case studies and 12 sensitivity analyses involved a total of 11 heat exchangers and five 12SH-13 water pumps.The flow rate was jointly regulated by adjusting the pump opening and closing quantities,VFDs,and valve opening degrees.The parameters related to the heat flow and 12SH-13 pumps can be found in the supplement.

The crossover probability and mutation probability in the genetic algorithm are set at 0.9 and 0.001,respectively,with a population size of 50.The model is programmed using Python 3.9.7 and executed on an AMD Ryzen 7 5800H CPU.The model is iterated for 10000 times in a single run,with an approximate runtime of 200 min.

3.1.Comparison of case with and without fouling consideration

3.1.1.Economic performance comparison of fouling and non-fouling

Fig.2 shows the cost of pump and tower of the three cases.In the non-fouling case,the total cost is 1.55×106USD,with pump cost of 5.87×105USD and cooling tower cost of 0.95×106USD.The total cost of fouling is 1.68×106USD,and the cost of the pump(sum of the operating of the pump and the investment of VFDs is 0.62×106USD,and the cost of the cooling tower is 1.05×106USD.The total cost increased by 8.0%.The operating cost of pump and cooling tower increased by 7.2% and 8.6%,respectively,mainly due to the weakening of heat transfer by fouling and the increase of pressure drop in the fouling case,which led to a larger water flowrate and a larger pressure drop in the system,thus resulting in higher operating cost of pump and cooling tower,as well as the cost of blowdown.In summary,in this case the fouling caused an additional economic loss of 8%.

Fig.2.Pump and tower cost of fouling,non-fouling and Cycle 5 three main cases.The capital cost of VFD is omitted owing to its low proportion.

3.1.2.Fouling situation

Fig.3 presents the variations in (a) fouling thermal resistance,(b)inner diameter,(c)concentration cycle,(d)fouling rate,and(e)flow velocity of the 11 heat exchangers in fouling case.The trend in fouling thermal resistance depicted in Fig.3(a)is determined by the fouling rate(Fig.3(d)).It can be observed that during the months of June,July and August(JJA),when the fouling rate is low,the fouling thermal resistance does not increase significantly.However,as the inlet water temperature decreases and the flow velocity decreases,the fouling thermal resistance starts to increase and reaches 6.9 × 10-4m2∙K∙W-1after three years.The variation in inner diameter of the heat exchanger tubes(Fig.3(b))corresponds to the fouling thermal resistance.The effective tube diameter no longer decreases during the JJA months,and the average inner diameter of the 11 heat exchangers decreases from 0.0154 m to 0.0137 m,which is a reduction of approximately 11%.

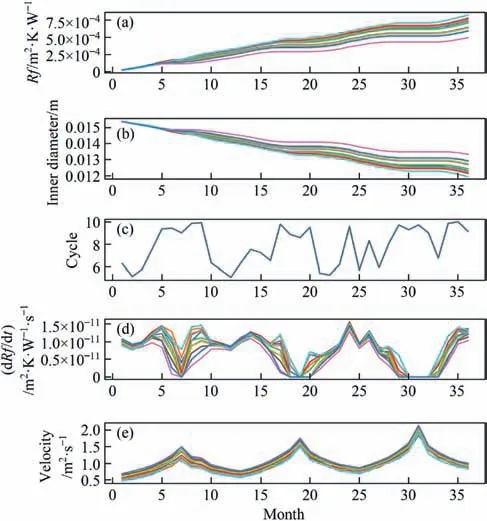
Fig.3.(a) Fouling thermal resistance,(b) inner diameter,(c) concentration cycle,(d) fouling rate and (e) flow velocity of the 11 heat exchangers in fouling case.

The trend and attribution of fouling rate and concentration cycle.The optimized concentration cycle varies between 5 and 10 over the three-year operation period(Fig.3(c)).The product of the concentration cycle and the initial ion concentration gives the actual ion concentration in the circulating water for each month.The optimized cycle is closer to its upper limit than its lower limit,indicating that the cost of water treatment dominates the selection of the cycle.The system tends to save water rather than inhibit fouling.This is related to the initial ion concentration setting,water treatment,and wastewater treatment costs.In Fig.3(d),the joint influence of fouling rate,temperature,flow velocity,and ion concentration(mainly cycle)reflects the trend of fouling rate variation.As temperature increases,the solubility of calcium carbonate decreases,and the calcium carbonate dissolved in the fluid begins to precipitate,forming a layer of deposit on the heat transfer surface,thus the fouling rate increases with temperature.The flow rate in Fig.3(e) shows seasonal oscillations,which corresponds to the thermodynamic effect of the heat exchanger and the hydraulic effect of fouling on the pipeline.The required cycle water flow rate increases with water temperature,so the optimal flow rate should show a seasonal oscillation that is related to water temperature.When the temperature increases,a larger cycle water flow rate is required to meet the heat transfer requirements,and a larger cycle water flow rate means an increase in flow rate,which will inhibit the fouling rate.However,the increase in flow rate compensates for the trend of increasing fouling rate caused by the temperature increase.In other words,the increase in environmental temperature promotes fouling to some extent,but it is not enough to completely compensate for the decrease in fouling rate caused by the high flow rate.The positive correlation trend of average flow rate over time is explained by fouling.Under long-term operation,the effective inner diameter decreases due to the accumulation of fouling layer,and the heat transfer effect is weakened.The joint effect of these two factors leads to an increase in the required cycle water flow rate,namely,an increase in inter-annual variability of flow rate,i.e.,an increase in annual average flow rate in long-term operation.Increased horizontal shear force accelerates the removal of calcium carbonate,causing particles to be carried away from the surface of the fouling layer,thereby reducing the fouling rate,which is macroscopically manifested as a stable or reduced thermal resistance.Therefore,the influence of flow rate will gradually increase in long-term operations until the fouling rate tends to zero and the fouling thermal resistance reaches its peak,i.e.asymptotic fouling resistance[23].Thus,in months with higher ambient temperatures(JJA in Fig.3(b)),the fouling rate is smaller.Compared with the first year,the seasonal cycle of flow rate in the second and third years shows a larger amplitude in Fig.3(e).In the warmer JJA months,there is a greater increase in water demand,while there is not much increase in flow rate during the winter months,implying that fouling may have a more significant impact during warmer seasons.

Differences in fouling among heat exchangers.The fouling rate varies among different heat exchangers and is related to properties of the heat flux,cooling water flow rate,wall temperature,and other factors.As shown in Fig.3(b)-(d),there are significant differences in fouling among the different heat exchangers.EX7 is the least prone to fouling,with an average fouling rate of 5.3 × 10-12m2∙K∙W-1∙s-1,and a fouling resistance of 5.0×10-4m2∙K∙W-1at the end of the third year.Its effective tube diameter only decreased by 13.4%.In contrast,EX10 is the most prone to fouling,with the highest average fouling rate of 8.8×10-12m2∙K∙W-1∙s-1among the 11 heat exchangers,which is 66% higher than EX7 and 20% higher than the overall average.Its fouling resistance at the end of the third year was 8.3×10-3m2∙K∙W-1,and its effective tube diameter decreased by 22.5% to 0.0119 m.The reason for the higher fouling rate in EX10 and lower fouling rate in EX7 is related to the removal rate of the fouling layer.The removal rate φrin EX7 is relatively high at 2.2×10-7kg∙m-2∙s-1,which results in a lower fouling rate despite a formation rate φdthat is slightly higher than the average among the 11 heat exchangers.On the other hand,the fouling rate in EX10 is highest due to a lower removal rate,despite not having the highest formation rate.During the three-year operating period,EX7 had the highest average flow rate at 1.14 m∙s-1,while EX10 had the lowest at 0.92 m∙s-1.The control of flow rate by branch valves played a dominant role in determining the removal rate and thus the fouling rate of different heat exchangers.

3.1.3.System operation comparison of fouling and non-fouling

Number of pumps,operation of valves,frequency of VFDs.The behavior of a system is affected not only by fouling and thermal effects but also by hydraulic effects,such as the number of pumps,valve operations,and frequency of VFD.Here,we analyze the system's operation under two scenarios: fouling and non-fouling,including the operation of CSPs,VSPs,and valve openings.Fig.4(a) and (c) compare the number of pumps under long-term operation in three different cases: fouling,non-fouling and Cycle 5.In the non-fouling case,where flow demand does not change annually,the number of pumps is always 2 or 3 (Fig.4 (a)).All three pumps are VSPs and installed with VFDs(Fig.4 (c)).In contrast,in the fouling case,the number of pumps increases from 2 to 3 in the first year to 2-4 in the third year.Only three of the four pumps have VFDs (Fig.4 (c)),with three VSPs and one CSP.The increase in annual flow demand requires more pumps to provide a larger flow.The total number of pumps and VFDs are similar in both scenarios,with one additional pump in fouling case,and three VFDs in both cases.The maximum and minimum values of the pump speed ratio k are 1.18 and 0.71,respectively,within the range of 0.7-1.3,with more pumps having k<1.The average resistance coefficient of the main pipeline valves is similar in both fouling and non-fouling cases,with slightly smaller resistance in fouling,indicating a more open overall valve.Fig.4 (b) shows that fouling is more severe,with the peak flow rate in July greater than in the non-fouling and Cycle 5 cases,indicating a greater effect of fouling on months with higher temperatures such as JJA (see Fig.5).

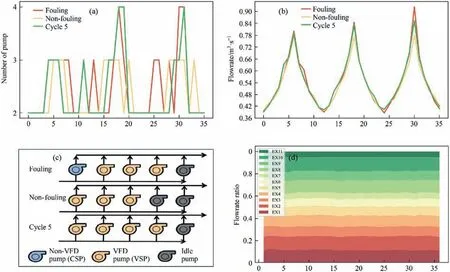
Fig.4.(a) Number of pumps,(b) water flow rate,(c) pump type of fouling,non-fouling and Cycle 5 three cases and (d) flow rate ratio of 11 exchangers in fouling.

Fig.5.(a) Fouling thermal resistance,(b) inner diameter,(c) fouling rate and (d) flow velocity comparison of fouling and Cycle 5.

Flow rate distribution differences in branches due to fouling.Fig.4(d)shows the flow rate ratio of 11 coolers in the fouling case.On average,EX1,EX2,EX8,and EX10 have a larger flow rate due to their property of exchanger (heat duty,number of tubes and area,etc.)and regulation by branch valves.The valve changes in EX1 and EX2 are greater,while EX7,which has the lowest fouling rate,has a smaller valve opening that remains almost fully open throughout the three-year operation period.Overall,the flow rate changes in the branches are not significant,which is related to the narrow range of the branch valve openings.

3.2.Comparison of case with variable and fixed concentration cycle

3.2.1.Economic performance comparison of fouling and Cycle 5

Fig.2 also presents the total cost and the cost breakdown of each component for both fixed and variable cycles,with a fixed ratio of 5.As expected,optimizing the cycle as a variable yield better economic benefit.The operation cost of pumps(green bar),the cost of wastewater treatment (milk green),and the cost of water supplementation (yellow) are slightly higher in Cycle 5 compared to fouling.The total cost for Cycle 5 is 1.73 × 106USD,with a total pump cost of 6.24 × 105USD and a total cooling tower cost of 1.09 × 106USD,which is 3.6% higher than fouling.Therefore,optimizing the cycle for each interval,compared to a fixed cycle,significantly improves the economic benefits of blowdown,water supplementation,and pump operation,leading to a 3.6%reduction in the total cost.

3.2.2.Fouling situation and trends of concentration cycle

The variation of concentration cycle reflects the trade-off between fouling and water treatment.As the concentration cycle increases,the concentration of dissolved substances also increases,which enhances the tendency of fouling.Higher concentration cycles can effectively reduce makeup water usage and promote water conservation,but they can lead to more severe fouling issues,requiring more frequent water treatment measures for prevention and removal of fouling.This,in turn,increases the risks of fouling and the cost of water treatment.On the other hand,lower concentration cycles can reduce the tendency of fouling but require more makeup water and water treatment to dilute the dissolved substances in the circulating water.Therefore,it is necessary to find a balance between fouling control and energy/water conservation through the cycle,ensuring lower flow velocities in the circulating water system,thereby achieving optimal economic benefits.

When the cycle is not fixed,it is possible to increase it during months with higher temperatures and larger flow rates to save water,while avoiding higher fouling rates.This approach is significantly better than the fixed cycle method.Here,we propose a formula to explain the effect of cycle variation on fouling rates.Ignoring other factors,fouling rate can be simplified as a function of temperature,flow rate,and ion concentration.The cycle determines the ion concentration in practical operation,which can be described by Eq.(47).Therefore,the variation in fouling rate can be explained by changes in temperature,flow rate,and concentration cycle.Here,we analyze the sensitivity of fouling rate to cycle,namely,the effect of changing the unit cycle on fouling rate.

Analysis of the formula for the calculation of precipitation rate φdin Eq.(32) shows that φdis approximately proportional to.Therefore,when the removal rate of calcium carbonate φris small,changes in cycle affect ion concentration,which further determines the rate of fouling formation dRf/dt.Flow rate affects φr,with a larger flow rate resulting in a larger φrand a lower rate of fouling formation.At this point,the sensitivity of fouling formation rate to cycle is low,and the cost of increasing cycle is also low.Therefore,the algorithm tends to increase cycle.In other words,in months with higher temperatures,the required amount of circulating water flow is larger,resulting in a higher flow rate and a tendency for the rate of fouling formation to approach 0,and thus a larger cycle in that month.When flow rate is dominant,changes in cycle have little effect on the rate of fouling formation,∂f/∂c ≈0,and increasing cycle can save water.This explains the seasonal peak of cycle in months with lower rates of fouling formation (JJA) in Fig.3(c).However,this tendency is also influenced by temperature and ion concentration,as well as the increased cost of water treatment associated with reducing cycle.When flow rate and temperature do not dominate the rate of fouling formation,the rate of fouling formation is approximately linearly positively correlated with cycle,i.e.,∂f/∂c ≈k,where k is a positive integer.This explains the linear relationship between cycle and rate of fouling formation in Fig.3(c) and (d) and the similar curve shape around the 25th month.In this case,increasing cycle promotes fouling formation,so it should be avoided as much as possible.However,the value of cycle is also influenced by water cost.In water-scarce or high-cost areas,a higher cycle can be chosen.Therefore,in months with larger demand of circulating water flow,i.e.,in warmer months such as summer,increasing cycle can save water while maintaining a lower rate of fouling formation.

This equation can also explain how to avoid fouling by controlling cycle under different temperature and flow rate conditions,and how to control fouling by adjusting flow rate under given temperature and cycle conditions.Establishing an accurate mathematical relationship between fouling and temperature,flow velocity,and cycle can be applied to optimize the design and operation of a circulating water plant,control fouling,and achieve the most efficient operation of the system.

3.2.3.System operation comparison of fouling and Cycle 5

Number of pumps,operation of valves,frequency of VFDs.In both fouling and Cycle 5,there was little difference in flow rate,the number of pumps and VFDs.Both had four pumps,and Cycle 5 had one more VFD than fouling,with four and three,respectively.The seasonal fluctuations in the number of pumps were also not significant (Fig.4 (a)).The monthly average cycle in fouling was 8.1,which was higher than that in Cycle 5.Thus,fouling case had a more severe long-term fouling problem.This can be seen that the flow rate in fouling was higher in July of the third year,with an increase of 12%,to 0.95 m3∙s-1,compared to 0.85 m3∙s-1in Cycle 5(Fig.4(b)).The range of pump speed ratio k in Cycle 5 was 0.7-1.1,slightly lower than the range of 0.71-1.18 in fouling.This may indicate that the algorithm was more inclined to reduce the frequency of pump operation in Cycle 5.

Flow rate distribution differences in branches due to fouling.In Cycle 5,similar to the fouling case,the valves of EX1 and EX7 were open to a greater degree.However,the valve of EX1 was slightly larger,leading to a 4%increase in its average flow rate compared to EX1 in fouling,while EX7's flow distribution decreased by 2%.The uneven flow rate distribution was partly due to differences in fouling impact among the heat exchangers [24].As fouling layers accumulate in the heat exchanger,the relative hydraulic resistance increases,resulting in a lower water flow rate,higher temperature,and increased fouling [24].In optimizing the flow rate,the algorithm adjusts the flow rate of heavily fouled heat exchangers by increasing the valve opening to compensate for the weakened heat transfer caused by fouling while inhibiting further fouling.However,it is challenging to quantitatively describe the contribution of these opposing trends to the flow rate.

4.Sensitivity Tests

To assess the robustness of the model,12 sensitivity analyses were conducted,including changes in the cycle and the inlet water temperature.The cycle varied from 2 to 10 in increments of 1 for a total of 9 groups,while the temperature range included 6-30°C(279.15-303.15 K),18-30°C (291.15-303.15 K),and 24-30°C(297.15-303.15 K),totaling 3 groups.When conducting sensitivity analyses with a fixed cycle,the water temperature was varied between 18 and 30°C(291.15-303.15 K),while the cycle was varied as the variable when analyzing the sensitivity to temperature.

4.1.Concentration cycle

4.1.1.Fixed concentration cycle

Optimum concentration cycle.Static changes in the cycle can have an impact on the heat transfer effect and heat exchanger fouling in long-term operation of circulating water systems.At the same time,the cycle is usually set as an isolated parameter in industrial operations to inhibit fouling and save circulating water consumption,ignoring its interaction with heat transfer and fouling.In order to verify the sensitivity of the model for a fixed cycle and to analyze the system operation and fouling at different cycles,nine sets of fixed cycles from 2 to 10 were set.To analyze the differences in system operation at static concentration multipliers,the economically optimal concentration multipliers and the corresponding heat exchanger network performance.

Fig.6 presents the total cost of system operation under nine cycles.Cycle 10 is excluded from the analysis due to incomplete heat duty caused by fouling(Fig.7).The results show that the total cost of the system decreases and then increases as the cycle increases,with a greater decrease in cost observed at higher cycles.The cost of pump operation gradually increases,while the cost of water supply and discharge also increases.As the cycle increases,the ion concentration also increases,resulting in lower water supply costs but a stronger fouling trend,making the circulating water more prone to fouling.Conversely,as the cycle decreases,the water consumption for makeup increases,and the ion concentration decreases,making it less prone to fouling,but increasing the cost of water supply and discharge treatment.The cycle represents the trade-off between fouling and water treatment in an operating cycle.However,as the cycle increases,the marginal benefit of water conservation decreases(Fig.6).In this case study,the optimal static cycle value is approximately between 4 and 6,and to obtain a more accurate value,additional cycles should be tested within this range.

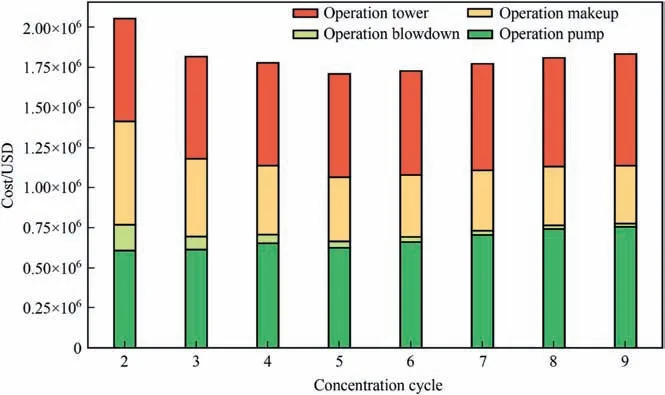
Fig.6.Pump and tower cost of nine concentration cycles.The sensitivity case Cycle 10 is omitted for its uncompleted heat duty because of fouling.

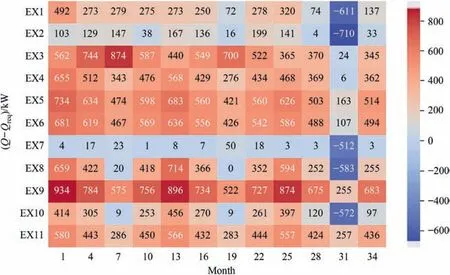
Fig.7.Difference between heat load and heat required for 11 heat exchangers at three month intervals starting from January.

Fouling and network performance variations in a concentrated water reuse system.The effects of cycle on fouling and network performance were investigated in a concentrated water reuse system.As the cycle increased,fouling became more severe and the annual variability of water demand increased,requiring greater flow rates to maintain heat transfer.The fouling rate displayed a clear pattern with cycle (Fig.8 (a)),increasing linearly in colder months but approaching zero in the three summer months of JJA,where flow velocity dominated.As the cycle increased,the seasonal variation of fouling thermal resistance became more pronounced (Fig.8 (b)).While the fouling resistance of Cycle 2 increased linearly,Cycle 9 experienced apparent stagnation in the three summer months,approaching asymptotic fouling resistance.In high-temperature months,flow velocity gradually became the dominant factor affecting fouling rate.It is worth noting that in Cycle 10,in July of the third year,five heat exchangers (EX1,EX2,EX7,EX8,and EX10) failed to meet their heat duty requirements(Fig.7).This was due to severe fouling,with thick fouling layers and high heat transfer coefficients on the water side causing significant interference with heat transfer.Increasing flow rates could no longer meet the heat transfer requirements,resulting in an inability to complete heat transfer tasks.Therefore,controlling the cycle and preventing severe fouling is necessary to ensure heat transfer requirements are met.

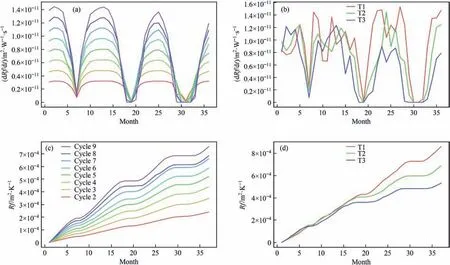
Fig.8.(a) Fouling rate,(b) fouling thermal resistance average of 11 exchangers from Cycle 2-Cycle 9,(c)fouling rate,(d)fouling thermal resistance of 11 exchangers from T1-T3.

Operational differences in the system.The monthly average flow rate in the nine cycle cases showed a small increase in water flow and little year-to-year variability,resulting in similar numbers of pumps and VSPs (approximately three to four) and variable frequency drives (VFDs) (Table 1).Despite the small differences in flow rates,fouling accumulation resulted in a clear increase in the average flow velocity from 0.87 m∙s-1in Cycle 2 to 1.00 m∙s-1in Cycle 5 and 1.09 m∙s-1in Cycle 9.The system pressure drop increased from an average of 226 kPa in Cycle 2 to a maximum of 257 kPa.The monthly average opening of the main pipeline and valves showed no significant differences over three years.However,EX1 and EX7 had difficulty meeting their heat duty requirements,and the valve opening of their respective branch lines was greater than that of other branch lines,distributing more flow.

4.2.Environment temperature

Based on the information provided,it appears that water temperature is a key factor affecting the flow rate and fouling in the circulating water system.Different geographic locations and seasonal temperature variations may result in significant differences in fouling and heat exchanger performance.To investigate the impact of seasonal temperature variations on the system,three different temperature differentials (T1,T2 and T3) were set,and the effects on fouling rate and heat transfer were analyzed.Fig.9 shows that as the average temperature increases and water demand increases,the total cost of the system also increases.Compared to T1,the total cost of T2 and T3 increased by 11.9% and 14.7%,respectively,with the operating costs of pumps showing a greater increase of 17%and 25%,and cooling tower operating costs increasing by 9% and 8%,respectively.

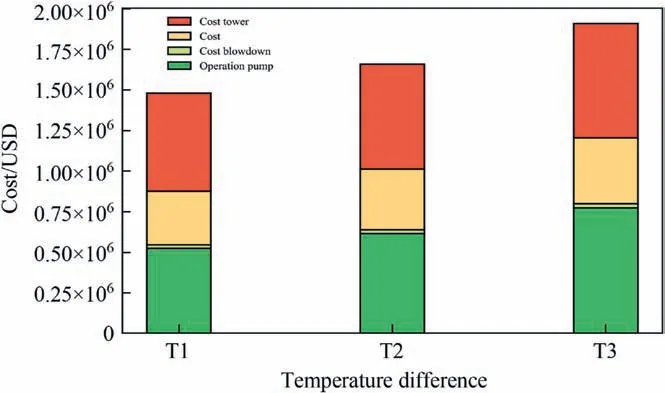
Fig.9.Pump and tower cost of three temperature differences.

The average fouling rates of 11 heat exchangers under three different temperature differentials exhibited three minima during the summer season (Fig.8 (c)).Interestingly,as the water temperature increased,the average fouling rate decreased,likely due to a more significant impact of water temperature on heat transfer.In the first 1.5 years,the difference in fouling thermal resistance was not significant (Fig.8 (d));however,over time,the difference between the fouling thermal resistance of the heat exchangers gradually became more apparent.After 18 months,the thermal resistance of T1 was only 17% higher than that of T3.Nevertheless,by 36 months,the Rf of T1 under its temperature differential(0.00086 m2∙K∙W-1) was nearly double that of T3(0.00053 m2∙K∙W-1).Following 18 months,the differences in fouling rates gradually increased (Fig.8 (c)).

Due to fouling,the seasonal amplitude of the average flow rate gradually increased,with T1 exhibiting a more significant increase(Fig.10).As the highest water temperature under the three temperature differentials was 30°C,the flow rate difference was not significant during this month.However,in the third year,the flow rate of T1 was significantly higher than that of T2 and T3,which was likely due to the more significant fouling effects and larger thermal resistance in T1.These findings suggest that,in warmer environments and seasons,the water circulation rate increases significantly to meet the heat transfer demands under high environmental temperatures,and the inhibitory effect of flow rate on fouling surpasses the promoting effect of temperature,resulting in a decrease in fouling rate.Additionally,large annual water temperature fluctuations may promote fouling.

Fig.10.Flow rate of T1,T2,and T3 during the three years operation.

5.Conclusions

This study proposes a mixed-integer nonlinear programming(MINLP) model considering the circulating water pump,pipes,dynamic concentration cycle,heat exchanger fouling,and variable frequency drive to optimize the configuration and operation of circulating water system.Sensitivity analysis of static concentration cycle and temperature is conducted,and the results demonstrate good sensitivity of the model,providing guidance for energyefficient optimization in the design and operation of circulating water systems.The following conclusions can be drawn.

(1) The proposed MINLP model optimizes the operation of the circulating water system by considering the interaction between the pump and piping system,fouling in the heat exchanger tube,and dynamic concentration cycle.The model obtains optimal operating parameters,including the concentration cycle,number of pumps,frequency of VFDs,and local resistance coefficient of valves,to minimize energy consumption and cost for different operating periods.On average,optimizing the concentration cycle can reduce total costs by approximately 3.6%.

(2) The concentration cycle fluctuates mainly between 5 and 10,indicating a system preference towards fouling rather than water conservation.This is influenced by initial ion concentration,makeup water,and water treatment costs.The economically optimal average monthly concentration cycle is 8.1.

(3) The interaction among cycle,temperature,and flow rate explains the trend of fouling rate.In warmer places and seasons,to meet the high heat exchange demand,the circulating water flow rate significantly increases,and the inhibition effect of flow rate on fouling exceeds the promotion effect of temperature,resulting in a decrease in fouling rate.In addition,larger inter-annual water temperature fluctuations may promote fouling.

(4) The concentration cycle represents the trade-off between fouling and water preservation.The dynamic optimization of concentration cycle has multiple benefits,such as fouling reduction,energy saving,and water conservation.However,as cycle increases,the marginal benefits of energy saving and water conservation decrease.In months with a small impact of cycle on fouling rate,including high-flow months with high environmental temperatures,water conservation can be achieved by increasing cycle while controlling the low level of fouling rate.

Declaration of Interests

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Yufei Wang reports financial support was provided by National Natural Science Foundation of China.

Acknowledgements

Financial support from the National Natural Science Foundation of China (22022816 and 22078358) are gratefully acknowledged.

Nomenclature

A the heat exchange area of the heat exchanger,m2

Ajparameter of the performance curve of pump j

Bjparameter of the performance curve of pump j

Cjparameter of the efficiency curve of pump j

cpheat capacity,J∙kg-1∙K-1

Djparameter of the efficiency curve of pump j

d inner diameter,m

Ejparameter of the efficiency curve of pump j

e roughness of the pipe,m

Fjparameter of the efficiency curve of pump j

g acceleration of gravity,kg∙m∙s-2

H supply head of pump,m

K overall heat transfer coefficient,W∙m-2∙K-1

k speed ratio of variable speed pump

kdconvective diffusion coefficient

krprecipitation rate coefficient

kspsolubility product,mol2∙L-2

l length,m

M mass flowrate,kg∙s-1

m number of heat exchange tubes

N number of tube passes

n sub-period month n

Q heat load of heat exchanger,W

R ratio of the smaller fluid heat capacity flow rate to the larger heat capacity flow rate of the heat exchanger

Re reynolds number

Rf fouling thermal resistance,m2∙K∙W-1

Sc schmidt number

T temperature,K

u velocity,m∙s-1

V flowrate,m3∙s-1

ΔP pressure drop,Pa

α convection transfer coefficient,W∙m-2∙K-1

ε heat transfer efficiency of heat exchanger

ζ local resistance coefficient of heat exchanger

η efficiency of pump

λ friction coefficient

ξ local resistance coefficient

πcconcentration cycle

ρ density of cooling water,kg∙m-3

φdformation rate,kg∙m-2∙s-1

φrremoval rate,kg∙m-2∙s-1

ψ deposition strength factor

ω 0-1varible,the opening of pump

Subscript

branch the branch of pipe

ex exchanger

i heat exchanger i

j pump j

t cooling tower

VFD variable frequency drive