基于功率动态分配与容量短期补偿的用户侧BESS复用策略

张圣祺，董静雯，王逸林，王 晛，张少华

（1.上海大学机电工程与自动化学院，上海市 200444；2.国网宁波市奉化区供电公司，浙江省 宁波市 315000）

0 引 言

近年来，风电光伏并网发电功率不断增长，电力系统常规电源调峰调频备用能力日益不足。此外，电力系统功率平衡和频率稳定还受到新能源汽车、高载能企业等负荷爆发式入网的威胁［1-2］。电池储能系统（battery energy storage system，BESS）得益于技术的快速发展，成为缓解电力电量不平衡的有效手段［3］。其中，由高载能企业所投建的用户侧BESS 电站已成为电力系统储能环节的重要组成部分［4］。相比于百兆瓦级的电源侧储能，用户侧BESS具有分布广泛、累积功率容量可观、投资分散等优势，是提升配电网内部灵活性［5］、实现新能源就地消纳［6］和助力“双碳”计划的关键。

用户侧BESS 除了作为备用电源外，还可跟随电力市场价格波动，通过峰谷套利降低用户购电支出［7-8］。然而，较高的建设维护成本和有限的峰谷电价差［9］，导致仅依靠峰谷套利无法提升用户侧BESS的经济性［10-11］。根据现阶段成熟市场的经验反馈，频率调节能够为用户侧BESS 提供更高的收益［12］。此外，2023 年10 月和11 月，广东省发展和改革委员会联合国家能源局南方监管局、内蒙古自治区能源局先后发布《南方（以广东起步）电力现货市场建设实施方案（试行）》［13］、《内蒙古自治区独立新型储能电站项目实施细则（暂行）》［14］。文件提出，建立“中长期+现货+辅助服务”的电力市场体系，配套容量补偿机制，促进储能电站有效回收投资成本。随着电力改革的深入和价格机制的完善，未来用户侧BESS 在调频辅助服务市场方面的经济性将进一步体现。考虑到日益增长的电网调频需求与调频市场提供的可观收益，用户侧BESS 面向峰谷套利和调频的复用模式成为提升其经济收益的重要发展方向。

上述复用模式兼顾了BESS 高能量密度和高功率密度的特性，最早被应用于BESS 功率容量规划的研究。文献［15］中BESS 参与能量和辅助服务市场，优化功率容量和替换周期。文献［16-17］分别基于时空联合优化方法和势函数重构法，实现复用模式下的BESS 规划。研究表明，复用模式能有效提高BESS 的经济收益，但基于历史数据的模拟运行不适用于实时调度。

由此可见，实现BESS 面向峰谷套利和调频复用的关键在于制定用于实时调度的BESS 功率复用策略。文献［18］将BESS 优先用于调频，当老化到一定程度后再参与峰谷套利。文献［19］利用电动汽车降低高峰时段电力需求，并在其余时段提供调频服务。显然，上述策略仅实现了对BESS 功率的分时复用。

针对BESS 功率在同时段的复用，部分策略预设了调度优先级。例如，文献［20］将BESS 功率优先用于频率调节，再根据用户侧负荷来决定调峰功率。相反，文献［21-22］则尽可能最大化调峰收益，再决定调频功率。然而电价存在波动，调度优先级无法跟随峰谷套利与调频收益的相对变化而改变。

于是，部分策略提出动态分配BESS 功率来提升经济收益。文献［23-24］以综合收益最大化为目标，通过划分3 个时间尺度，联合优化BESS 参与峰谷套利和调频运行，分配各场景功率。文献［25］建立了峰谷套利与调频联合优化框架，使用户用电支出降低了12%。然而，电网调频需求在上述策略中默认是已知量，完全忽略了其在实际中的随机性。

按照现有调度规则，BESS 需在调度周期前上报每个运行时段内参与调频市场的调差系数，表征可用调频功率，并在实时调度中始终以约定的调差系数持续响应频率偏差信号［26］。该功率更新周期与调频价格保持一致，电网可根据上报调差系数和调频价格，向BESS 结算调频服务费用。由于频率偏差信号的随机性，当出现所需调频功率大于可用调频功率时，BESS 可以通过优先满足调频功率，并延迟提供峰谷套利功率的方式避免功率越限。然而，BESS 容量越限在复用模式下却难以避免。调频不占用BESS 容量的理想情况下，会受到信号随机性和电池充/放电效率的影响，累积产生容量偏差。同时，峰谷套利所占用的BESS 容量又为刚性约束。为此，机会约束规划法［27-29］可以通过保守的BESS 充放电功率决策，间接降低容量越限风险。然而，即使对仅参与调频的BESS 采用较保守的决策，仍无法彻底避免容量越限。除上述问题外，考虑频率偏差信号随机性，会直接影响现有的动态分配BESS 功率复用策略中调差系数的取值，现阶段尚无研究提出有效的解决方案。

综上所述，为使复用策略更加符合实际工况，本文兼顾电价时变性和调频需求随机性，提出了基于功率动态分配与容量短期补偿相结合的BESS 峰谷套利与调频复用策略，实现了最大化BESS 日内收益的目标。该策略基于日前电价、调频价格与历史频率数据，通过分层求解形成以BESS 套利功率、调差系数、容量补偿系数为核心参数的调度结果，既能够有效提升BESS 收益，又能够避免调度周期内的容量越限。

1 面向峰谷套利与调频的BESS 复用策略

为匹配日前电价更新周期，策略将日内分为I个小时级时段，用i=1，2，…，I表示，间隔为Δt，更新套利功率与调差系数。选择介于峰谷套利和调频之间的分钟级时间尺度设置容量短期补偿周期，将i时段分为J个时段，用j=1，2，…，J表示，间隔为Δτ，更新容量补偿系数。

考虑到容量计算精度无须采用秒级数据，本文为简化模型假设频率偏差量Δfi，j在Δτ时段内保持不变，并与容量短期补偿周期一致。同时，将充/放电效率前置于频率偏差量中，如式（1）和式（2）所示。

式中:f（t）为秒级时间尺度电网频率；fnom为基准频率；Δfmax为频率偏差的最大值；Δfi，j，ave为Δτ时段内频率偏差量的平均值；ηc、ηd分别为BESS 充、放电效率。Δfi，j，ave∈［-1，1］，当偏差平均值大于1 时，取极限值1；当偏差平均值小于-1 时，取极限值-1。

BESS 面向峰谷套利和调频复用的实际充放电功率Pi，j，B为峰谷套利功率Pi，E、调频功率Pi，j，FR、补偿功率Pi，j，cmp三者之和。

式中:ri为调差系数，表征BESS 在时段i内的可用调频功率；Pi，j，cmp为时段i中分时段j内，BESS 因响应i时段中分时段0～k内频率偏差信号所需补偿的容量偏差；di，j为时段i中分时段j内容量补偿系数矩阵；Δfi为时段i中分时段j时段内频率偏差量矩阵。

式（3）—式（5）中，Pi，E受日前电价波动影响，在Δt时段内保持不变。Pi，j，FR以Δt时段内恒定的调差系数响应频率偏差信号。补偿功率Pi，j，cmp为不产生收益的BESS 预留功率，以Δτ为周期抵消BESS 参与调频所累积的容量偏差。

基于功率动态分配与容量短期补偿的BESS 复用策略可描述为以BESS 日内收益最大化为目标，以功率和容量为约束条件，求解核心参数Pi，E、ri、di，j的优化问题，如式（6）—式（9）所示，并记作OP0。由于功率分配与容量短期补偿在时间尺度上存在差异，OP0被拆解为2 个子策略分别求解，即功率动态分配子策略OP1和容量短期补偿子策略OP2。

功率动态分配子策略OP1基于日内电价和调频价格，通过预估调差系数r′i，实现BESS 功率在峰谷套利与调频之间的动态分配，并确定Pi，E。容量短期补偿子策略OP2则基于历史频率数据和套利约束，求解di，j并修正ri。

式中:V为日内I个时段峰谷套利和调频收益的总和；Pi，j，B≥0 时表示BESS 的充电功率，Pi，j，B＜0 时表示放电功率；ξ{·}函数在*事件成立时取1，反之取0；πi，E为日前电网售电价格，即BESS 参与电能买卖的价格；πi，FR为BESS 参与调频的价格，更新周期与πi，E保持一致；Si，j为BESS 在时段i中分时段j末的容量；Pmin、Pmax分别为BESS 充放电功率最小值、最大值；Smin、Smax分别为BESS 容量最小值、最大值，BESS 在实际运行中容量波动范围通常在10%～90%之间。

1.1 OP1模型

OP1用于确定BESS 的Pi，E，即用户侧BESS 在电价低谷时段所购入的电能，用于满足电价高峰时段的耗电需求。在小时级时间尺度内，可将OP0转化为如式（10）—式（15）所示的OP1，即已知电价波动曲线，以日内收益VE最大化为目标，Pi，E为决策变量的优化问题。由于OP1中仅涉及小时级时间尺度，故将Si，j记为Si，E。

考虑到峰谷套利价格的时变性，OP1通过预估调差系数r′i，使决策变量Pi，E的取值能够随着峰谷套利与调频收益的相对大小动态调整，从而实现BESS 功率在峰谷套利与调频之间的动态分配。在i时段内，Pi，j，FR受随机变量Δfi，j影响所带来的容量偏差最终会在OP2中被Pi，j，cmp抵消，即Pi，E是OP1中Pi，j，B在i时段内的平均值。式（10）在计算套利收益时采用Pi，E替代Pi，j，B。

式中:Sini、Sfin分别为BESS 在日内的起始、终止容量，可事先设置；α为BESS 仅参与调频时，调差系数与最大功率的比值，为经验系数。

在预估r′i时未考虑频率偏差量的随机性，为避免BESS 在调频服务中出现容量越限，ri的最终取值需通过OP2进行修正。

1.2 OP2模型

OP2用于在调度周期前基于历史调频数据确定用户侧BESS 在下个调度周期内的最大ri，以及为避免BESS 以ri响应频率偏差信号时出现容量越限所需的容量补偿系数矩阵Di。由于调频信号的随机性，在技术上避免容量越限、保障BESS 持续响应能力的同时，最大化ri以获得最大的经济收益，是OP2所解决的问题核心。

OP2需满足2 个必要条件:

1）BESS 应完全响应频率偏差。故将式（7）中Δfi，j统一取极值1 或-1，得到约束条件如式（16）所示，代入式（5）消去容量补偿功率Pi，j，cmp得到式（17），其中，Di是由i时段容量补偿系数矩阵di，j组成的矩阵，如式（18）所示。

2）为避免调频的随机性需求占用峰谷套利容量造成收益损失，新增约束条件，如式（19）所示，即BESS 充放电功率Pi，j，B曲线与时间轴所围面积不变。

OP2可描述为在i时段内，以调差系数ri最大化为目标，BESS 功率和容量不越限，且时段首尾容量不变为约束条件，求解ri以及合适的容量补偿系数矩阵Di的优化问题，如式（20）所示。此外，Pi，j，cmp对容量的调整仅针对前序频率偏差信号［Δfi，1，Δfi，2，…，Δfi，j-1］，不涉及当前时刻，确保容量补偿功率不会与当前时刻的调频功率抵消，从而使BESS失去调频效果。

图1 所示为BESS 复用策略及其分层求解架构示意图。

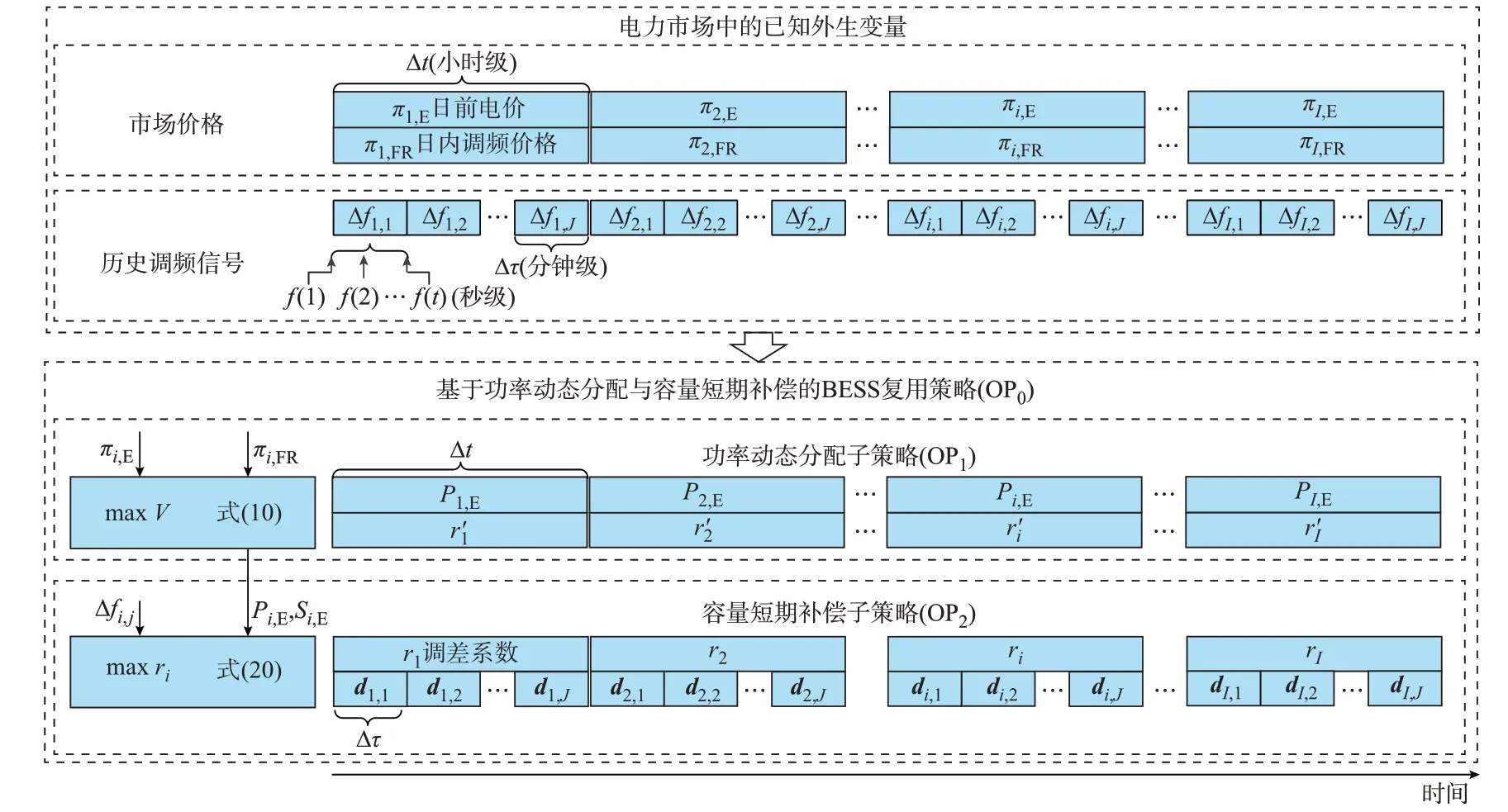
图1 BESS 复用策略及其分层求解架构示意图Fig.1 Schematic diagram of hierarchical solution architecture and multiplexing strategy for BESS

2 BESS 复用子策略参数求解方法

针对OP1采用动态规划作为求解方法，获得每个时段内的套利功率Pi，E与首尾时刻的BESS 容量Si，E。采用机会约束规划求解OP2，获得BESS 调差系数ri与容量补偿系数矩阵Di。OP1算法的求解过程如下:

步骤1:令i=I，ΔSi，E=Smin，Pi，E=Pmin；

步骤2:对∀Si，E∈{Smin，…，Smin+nΔS，…，Smax}，ΔSi，E=ΔSi，E+1；

步骤3:Pi，E=Pi，E+1；

步骤4:计算每个决策下储能当前阶段总收益Vi，E；

步骤5:计算当前时段i到最终时段（i=I）的累计收益；

步骤6:据累计收益大小更新当前容量状态下的最优决策；

步骤7:当Pi，E≥Pmax时，转步骤8，否则转步骤3；

步骤8:当ΔSi，E≥Smax时，转步骤9，并记录每个容量状态的最优决策，否则转步骤2；

步骤9:当i≤1 时，转步骤10，否则令i=i-1，转步骤2；

步骤10:令i=1；

步骤11:获取初始容量Sini；

步骤13:当i≥I时，结束，否则令i=i+1，转步骤11。

2.1 OP1参数求解方法

定义BESS 套利功率Pi，E为决策变量，Yi=［Si-1，E，πi，E］为状态变量，表示BESS 在i时段的状态，与i-1 时段终止时BESS 容量Si-1，E和该时段售电价格πi，E相关。BESS 容量被N等分，Si-1，E=Smin，…，Smin+nΔS，…，Smax，离散步长ΔS=（Smax-Smin）/N，n=1，2，…，N-1。BESS 容量状态转换公式如式（21）所示。

在i时段中遍历N+1 个容量状态，寻找并记录每个容量状态的最优决策。判断一个决策是否最优的依据是BESS 从当前时段i至最终时段I的累计收益大小。

同时，考虑到每个时段i的起始状态也是上一时段i-1 末的BESS 容量状态，由时段i-1 的起始BESS 容量与该时段的最优套利功率决定。由此递推可知，只需完成一次自前向后的最优解提取，即从时段1 的起始容量Sini开始，不断向后提取每时段的最优决策直到时段I为止，便可得到I个时段的Pi，E，与Si，E组成一天范围内的最优策略，也即OP1的解。

2.2 OP2参数求解方法

根据机会约束规划求解方法，首先将与随机变量Δfi，j相关的约束条件式（8）、式（9）、式（17）、式（19）改写为机会约束形式，如式（24）—式（29）所示。考虑到Δfi，j的随机性使得式（19）中Si，J未必能达到预设目标Si，E，在式（28）、式（29）中设置了允许的容量偏差范围。为便于表达，进一步将式（24）、式（25）统一成如式（30）所示的形式。

式中:Pr（·）为事件发生的概率；ϵ为给定的置信水平，取10-4～10-6；E为J阶单位矩阵；β为时刻i中分时段J内BESS 容量偏差占总容量的最大值；为与随机变量相乘的量组成的系数矩阵；bm是与随机变量无关的量组成的系数。

文献［30］中介绍的鲁棒优化方法来创建以上机会约束条件的安全近似。其思想是通过对频率偏差Δfi∈F的不确定性集F进行设计，确保式（30）始终成立，同时具有求解上的可行性。针对该不确定性集，要求约束式（24）—式（29）始终满足式（31）。

该方法的关键在于利用频率偏差信号的历史数据，通过基于向前偏差σi，j，f和向后偏差σi，j，b的不确定性集为ϵ确定最紧边界，进而将机会约束条件转化为确定等价类进行求解。但该方法仅适用于均值为零的随机变量，而实际频率偏差信号一般为非零平均信号。因此，需先将历史频率偏差信号进行白变换，得到均值为0 的变量Δfi，如式（32）所示。进一步利用式（32）、式（33）求取向前偏差与向后偏差，形成对角矩阵Q=diag[σi，1，f，…，σi，J，f]，R=diag[σi，1，b，σi，2，b，…，σi，J，b]。最后，结合求得的参数，可将机会约束转化为如式（35）所示的不等式约束［31］。至此，OP2中的机会约束条件经上述变换后，可转化成为一个不含随机变量的二阶锥问题，通过MATLAB 中的cvx 工具箱直接求解。

式中:W为将Δfi的协方差矩阵ΣΔfi取逆之后进行乔莱斯基分解后所得矩阵；为Δfi的平均值；sup（·）为上确界函数；E（·）为数学期望函数；θ为正实数，可以通过线性搜索并求解采样数据的经验平均值来近似代替期望值，从而找到最优值以获得上确界。

OP2算法的求解过程如下:

步骤1:基于历史调频信号，根据式(32)—式(34)计算集合参数矩阵W、Q、R；

步骤2:令i=1；

步骤3:获取OP1的调度结果Pi,E和Si,E；

步骤4:计算可用的储能资源，确定调频容量与功率约束，并改写机会约束式(24)—式(30)；

步骤5:利用集合参数重构约束式(35)，结合式(20)组成二阶锥问题；

步骤6:利用cvx 工具箱求解得到ri,Di；

步骤7:当i≥I时，结束，否则令i=i+1，转步骤3。

3 BESS 复用策略的仿真验证与分析

为验证基于功率动态分配与容量短期补偿的用户侧BESS 复用策略的可行性、优越性，在MATLAB 仿真环境下模拟BESS 参与峰谷套利与调频运行。设定用户侧BESS 额定功率为0.5 MW，额定容量、Smin、Smax分别为1、0.1、0.9 MW·h，日内起始和终止容量Sini=Sfin=0.5 MW·h，ηc、ηd分别为0.9、0.95。同时，设定日内时段数I为48，对应Δt为30 min，J为6，对应Δτ为5 min。

部分关键参数取值如下:基准频率fnom为50 Hz，频率偏差最大值Δfmax为0.2 Hz，系数α为0.7，β为0.05，置信水平ϵ=10-4。选取澳大利亚电网［32］2021年4 月至8 月某典型日日前电价数据，经货币换算后见图2（a）。频率偏差信号则根据该典型日频率数据并计及充放电效率所得，如图2（b）所示。该典型日日内调频价格均值约为30 元/（MW·h），波动范围约为-15～15 元/（MW·h）。为更直观的表现调频价格与日前电价的相对变化，及其对BESS 调度的影响，假设调频价格在日内为定值，故省略下标j，记为πFR。完全基于该典型日实际调频价格的OP0调度结果见附录A。

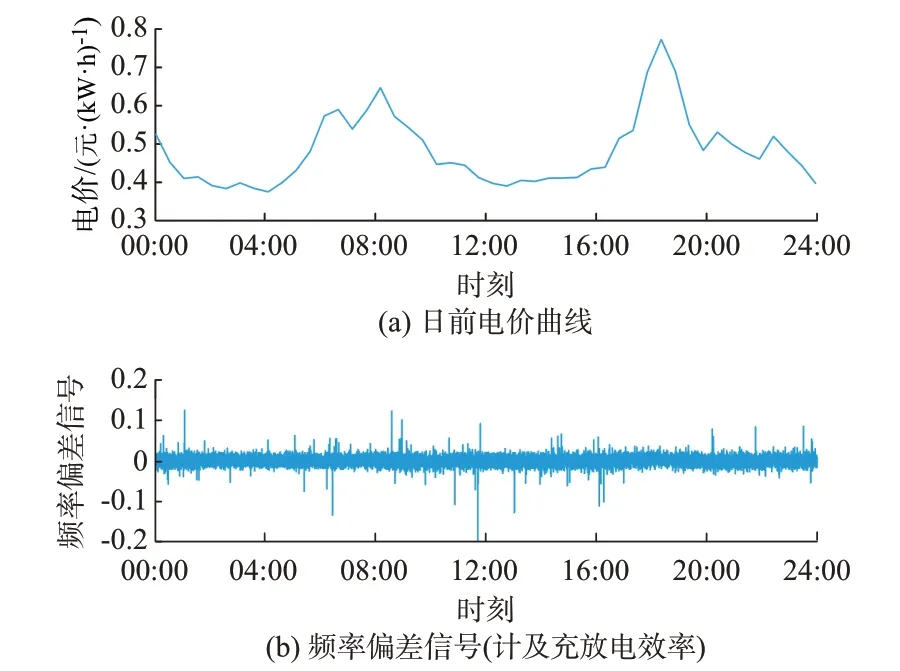
图2 日前电价曲线与频率偏差信号Fig.2 Curve of day-ahead electricity price and signals of frequency deviation

3.1 复用策略功率动态分配及验证

在上述仿真环境基础上，将日内调频价格πFR分别设置为15、30、45 元/（MW·h），开展对比仿真。图3 所示为不同调频价格下，BESS 套利功率Pi，E、调差系数ri、套利和调频占用容量百分比。

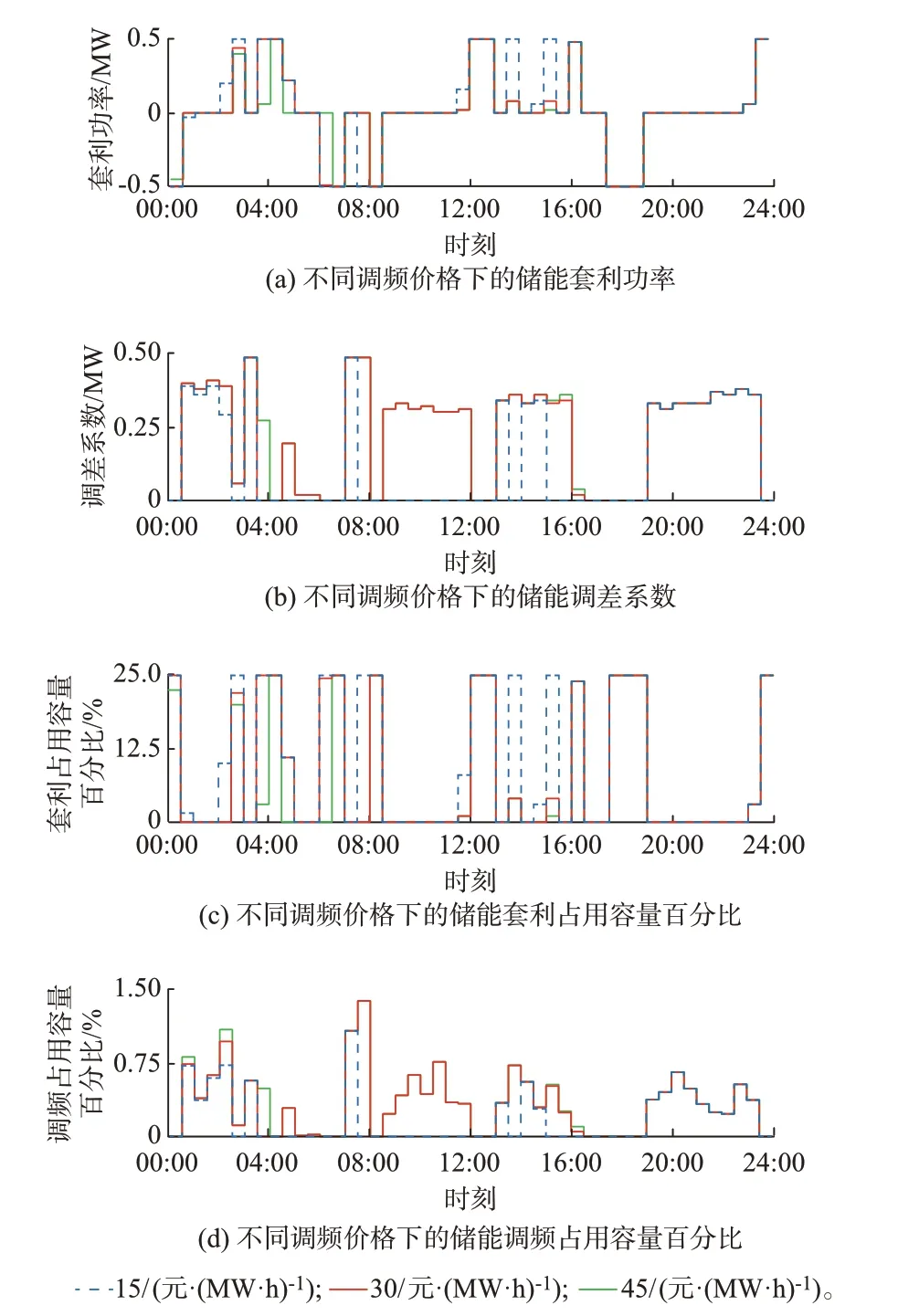
图3 不同调频价格下的BESS 运行参数曲线Fig.3 Curves of BESS operation parameters under different frequency regulation prices

以日内调频价格πFR=30 元/（MW·h）为例，BESS 峰谷套利功率变化曲线如图3（a）所示，具体数值见附录B 表B1。由图3（a）可见，BESS 在电价低谷时段02:30—05:00 和12:00—16:30 充电，电价高峰时段06:00—08:30 和17:30—19:00 放电。上述充放电行为符合套利功率Pi，E与日前电价呈明显相关性的特点。

BESS 参与调频的调差系数ri如图3（b）所示，具体数值见附录B 表B2。对应日前电价曲线，当处于电价高峰时期，即πi，E相对πFR较大时，BESS 大部分功率用于套利；而处于电价低谷时期，即πi，E相对πFR较小时，BESS 选择更多地参与调频服务和相对更大的调差系数。上述结果初步符合根据电价时变性动态分配BESS 功率的预设。

基于上述调度结果，BESS 响应频率偏差信号后，峰谷套利和调频所占用的容量百分比如图3（c）和图3（d）所示。日前电价低谷时段（13:30—14:00）、日前电价适中时段（00:30—01:00）、日前电价高峰时段（07:30—08:00），3 个典型时段的峰谷套利功率、调差系数和套利与调频占用容量百分比如表1所示。需注意，占用容量百分比是指该时段峰谷套利或调频所需的最大容量占BESS 额定容量的比值，非累计容量。

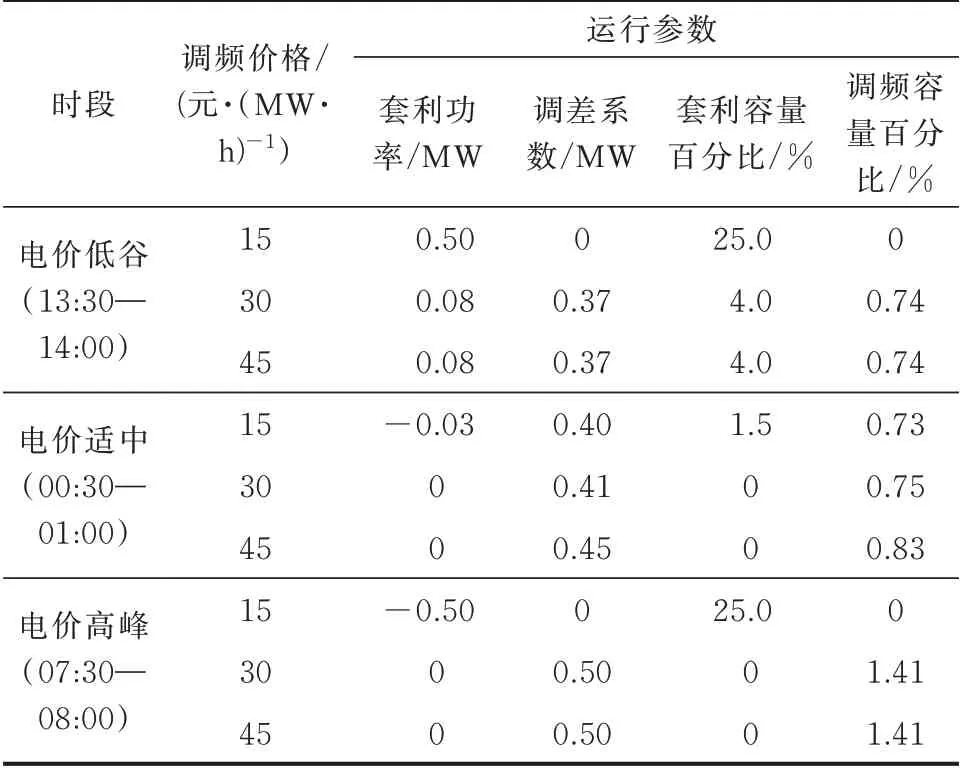
表1 不同调频价格下的BESS 运行参数Table 1 Operation parameters under different frequency regulation prices

在电价高峰时期，BESS 套利占用的容量百分比随着调频价格的增大逐渐从25%降为0，BESS功率逐步不倾向于峰谷套利，直至完全用于响应调频偏差信号。在电价低谷时期，有同样类似的情况。可见，OP0策略能够根据峰谷套利和调频收益的相对变化，实现BESS 功率的动态分配，并在容量占比上有所体现。

为进一步体现OP0策略能够实现对BESS 功率的动态分配，设置峰谷套利优先复用策略OPEA和调频优先复用策略OPFR。OPEA是指最大化BESS 峰谷套利收益后，叠加剩余资源参与调频收益；OPFR是指最大化调差系数后，叠加考虑调差系数约束的峰谷套利收益。不同调频价格下，基于OPEA和OPFR策略的BESS 套利和调频占用的容量百分比曲线见附录C。结果表明，OPEA和OPFR策略在不同调频价格下呈现相同的运行结果，即OPEA和OPFR策略无法跟随峰谷套利和调频收益的相对变化，动态调整BESS 资源分配。关于经济性的对比将在3.3节进一步展开分析。

3.2 容量短期补偿必要性分析

通过对比复用策略OP0与未包含容量短期补偿的OP′0复用策略，验证容量短期补偿的必要性。OP′0采用与OP0一致的Pi，E和ri计算方法，并设置Di=0。日内调频价格πFR=30 元/（MW·h）。

首先得到OP0策略中容量补偿系数矩阵Di在典型时段下的取值及调差系数。

00:00—00:30 时段OP0策略中容量补偿系数矩阵Di如式（36）所示，其对应的ri=0 MW，BESS 未参与调频，无需容量补偿。因此，Di为全零矩阵。

00:30—01:00 时段OP0策略中容量补偿系数矩阵Di如式（38）所示，其对应的ri=0.41 MW。

05:00—05:30 时段OP0策略中容量补偿系数矩阵Di如式（37）所示，其对应的ri=0.02 MW。

采用两种复用策略时，BESS 容量变化曲线如图4 所示。

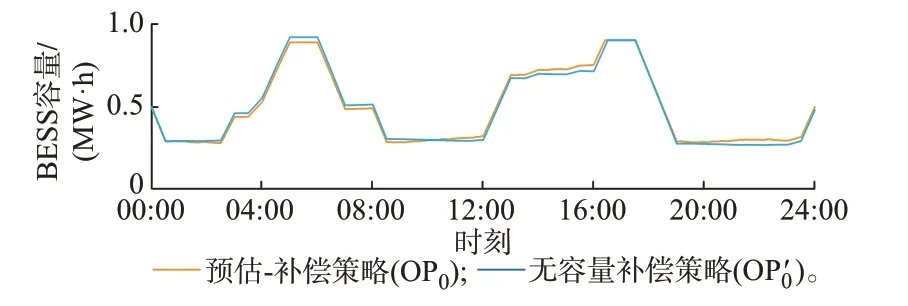
图4 BESS 采用两种复用策略时的容量曲线对比Fig.4 Comparison between capacity curves of BESS with two multiplexing strategies

对比仿真结果，OP′0策略在时段05:00—06:00中出现了容量越限，而该现象并未在OP0策略中发生。原因在于，容量短期补偿抵消了以固定调差系数完全跟踪频率偏差信号所产生的容量偏差，使得BESS 实际运行时的容量变化贴近功率动态分配子策略OP1的决策结果，彻底避免了容量越限问题。仿真结果表明，尽管容量补偿系数矩阵取值较小且以0 为主，但是在BESS 持续满足调频需求，避免容量越限中扮演了重要角色。因此，基于容量短期补偿的OP0策略具有在追求收益最大化的同时保障BESS 持续可用调频容量的能力。

3.3 复用策略经济优势分析

最后，通过仿真对比用户侧BESS 采用不同复用策略所获得的收益，以验证OP0在提高综合收益上的优越性。对比用户侧BESS 采用OP0、OPEA、OPFR和OP′0四种复用策略在不同调频价格πFR下的收益，结果如表2 所示。仿真结果表明，BESS 采用OP0的收益始终高于OPEA和OPFR。原因在于OP0能够根据峰谷套利和调频收益的相对变化，动态调整BESS 的功率分配。

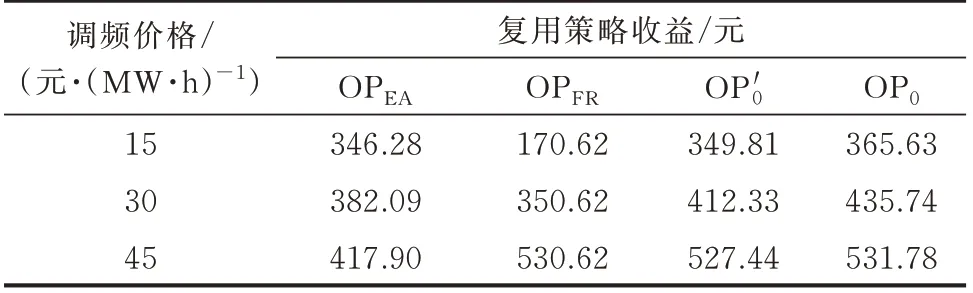
表2 4 种复用策略在不同调频价格下的收益对比Table 2 Comparison between profits with four multiplexing strategies under different frequency regulation prices

BESS 采用OP0的收益均高于采用OP′0的收益。收益的增加来源于OP0中参与调频的时段较OP′0更多，且每个时段调差系数的取值均大于等于OP′0，如图5 所示。原因在于:容量短期补偿抵消了频率偏差信号随机性所带来的容量偏差，使得BESS 在调频越限概率（置信水平ϵ）相同的情况下，能够提供更多的调频容量，获得更多收益。由此可见，基于功率动态分配与容量短期补偿的BESS 峰谷套利与调频复用策略在提高用户侧BESS 收益方面具有优越性。

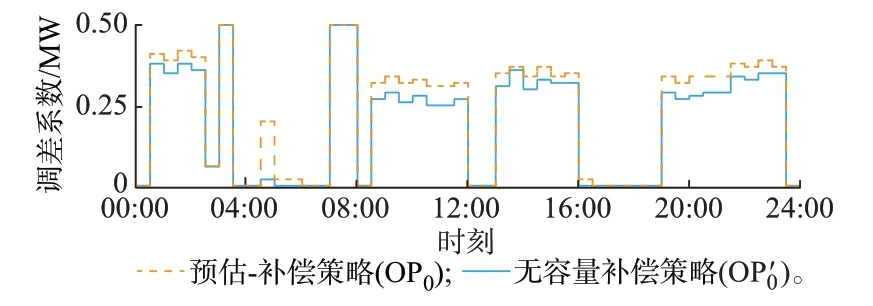
图5 OP0策略和OP′0 策略的调差系数对比Fig.5 Comparison between droop coefficients with OP0 strategy and OP′0 strategy

3.4 国内电力市场可行性分析

区别于国外成熟辅助服务市场，中国将调峰计费归于辅助服务。由于中国现货市场起步较晚，尚未能通过市场化手段达到削峰填谷的作用，故设置调峰补偿激励电力企业提供调峰服务。将OP0策略收益模型式（6）更新为式（39）后，同样适用于中国国内电力市场。设置削峰补偿单价πf=0.4 元/（kW·h），填谷补偿单价πg=0.5 元/（kW·h）［33］，调频价格按30 元/（MW·h）。OP0策略产生的调度结果如图6 所示。

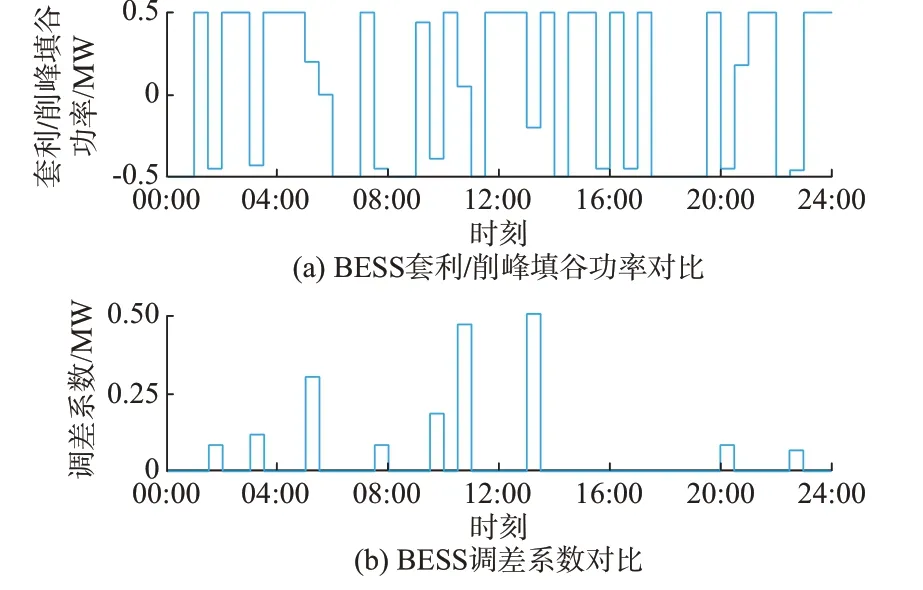
图6 基于OP0策略的BESS 套利功率和调差系数Fig.6 Arbitrage power and droop coefficients of BESS based on OP0 strategy

仿真结果表明，与3.1 节调度结果相比（见图3），考虑调峰补偿的OP0促使BESS 更多地参与峰谷套利，原因在于引入调峰补偿削弱了调频收益的相对竞争力。但随着中国电力现货市场改革的深入和辅助服务市场机制的不断完善，调峰补偿必然会退出历史舞台。本文讨论了峰谷套利和调频定价对BESS 调度的影响，对于利用市场手段引导BESS 资源动态分配，有重要的参考价值。

4 结语

为提高用户侧BESS 收益，实现BESS 资源的充分利用，本文针对其面向峰谷套利与调频复用提出了以套利功率、调差系数与容量补偿系数为核心参数的复用策略，并通过仿真验证了该调度策略具备以下优势:1）所提复用策略能够考虑峰谷套利价格的时变性，动态调整BESS 功率的分配；2）所提复用策略能够考虑调频需求的随机性，引入容量短期补偿，有效避免了BESS 运行中发生容量越限；3）所提复用策略通过功率动态分配和容量短期补偿的结合，显著提高了复用模式下BESS 的综合收益。

本文所述策略涉及BESS 运行时间尺度较短，尚未对BESS 充放电行为对其运行寿命的影响进行量化。未来，可以进一步研究计及电池老化成本的用户侧BESS 调度策略。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。