考虑用户出行成本预算的电力-交通耦合网络充电站定价策略

谢龙韬，谢仕炜，陈铠悦，张亚超，陈之栋

（福州大学电气工程与自动化学院，福建省 福州市 350108）

0 引言

随着中国新能源汽车发展战略的实施，电动汽车销售数量从2020 年的136.7 万辆增加到2022 年的688.7 万辆，占到了汽车市场销售总量的25%以上［1-2］。为适应电动汽车规模化的发展趋势，国务院办公厅发布的《关于进一步构建高质量充电基础设施体系的指导意见》［3］中指出，中国将于2030 年基本建成覆盖广泛、规模适度、结构合理、功能完善的高质量充电基础设施体系，来支撑电动汽车行业的发展，有效满足电动汽车用户的出行充电需求。随着电动汽车大规模普及，充电负荷的大量并网对电网的经济性、稳定性以及电能质量等方面都造成了严重的影响［4］。电动汽车充电站作为提供充电服务的设施载体，通过制定充电站充电价格，能对电动汽车的充电行为进行调控，从而实现负荷的有序充电，提高电网的经济性，其将对未来构建高质量充电基础设施体系起到关键作用［5］。

为制定有效的充电价格策略，需要关注电力-交通网络中的充电负荷分布情况。目前，电力交通领域已有不少文献对电力网与交通网融合的网络负荷分布特性进行了研究［6］。文献［7］表明网络的用户均衡状态能够有效描述电力-交通耦合网络的流量状态分布。文献［8］进一步将用户均衡问题转化为变分不等式问题，为求解电力-交通耦合网络用户均衡状态提供了有效的解决方案。

基于上述对于电力-交通耦合网络中用户充电行为的分析，对于充电站定价问题，文献［9］以无线充电技术为背景，研究了电网经济运行情况下的能源价格制定方法。文献［10］考虑存在一个独立的系统管理者，建立双层充电价格优化模型，通过电力网和交通网的协同运行，实现系统的最优运行。文献［11］以充电站运营商利益最大化为目标，提出了电动汽车充电站的定价机制。文献［12］为实现耦合网络资源的有效利用，提出了一种电动汽车充电价格补贴的方法。文献［13］从全局决策者的角度，以系统最优运行为目标，提出了电力-交通耦合网络的协同定价策略。文献［14］进一步考虑了混合需求不确定性，提出了电力-交通耦合网络的定价策略。文献［15］考虑了多个充电站运营商竞价的情况，建立了充电站定价非合作博弈模型。文献［16］通过变分不等式对网络的用户均衡状态进行描述，通过不动点映射的方法获得充电站充电定价方案。

上述研究通常是从价格制定者的角度出发，分析定价问题的有效性。然而，当前充电定价策略相关研究中，通常是将用户的出行需求视作常数，少有考虑到实际用户需求和行为对价格策略造成的影响。实际中，交通网出行用户具有一定心理预期，当交通拥堵、充电成本升高等因素导致出行实际成本大于用户预期的出行成本时，用户出行意愿可能发生变化，从而改变网络整体的出行充电需求。显然，忽略用户出行行为和需求变化前提下的定价策略将不符合实际情况，导致定价策略的有效性较低［5-16］。此外，现有研究对于电力-交通耦合网络充电站的定价问题，所构建模型通常存在非凸非线性约束［15-16］，传统的优化方法难以适用［14］。

基于现有研究所存在的不足，本文提出了一种考虑用户出行成本预算（travel cost budget，TCB）的充电站定价模型。首先，建立了考虑用户出行成本预算的电力-交通耦合网络充电站定价模型，利用交通网用户均衡与变分不等式的等价性，将定价问题等效为一类含有变分不等式约束的优化问题（optimization problem with variational inequality constraint，OPVIC）。其次，利用模型变量的可分离性，设计了一种交替迭代算法对等效问题进行求解。最后，采用56 节点配电网和28 节点交通网进行仿真，验证了问题建模与算法求解的有效性。

1 含电动汽车的交通网络建模

本文采用有向图GT(NT，A)来表示含电动汽车充电站的交通网络拓扑结构。其中，NT为交通网的节点集合，充电站的节点集合记为NCS⊂NT，A=Ac⋃Ar为交通网的路段集合，Ac为充电路段集合，Ar为通用路段集合。

考虑交通网络中所有用户从源节点出发前往终节点，其中电动汽车用户需经过一个充电站进行充电。为描述上述静态交通网络的车流量分布，本文进行了如下定义:将存在出行需求的用户按是否存在充电需求进行划分，将有充电需求的电动汽车归为电动汽车用户，记作用户e∈E，将无充电需求的电动汽车以及非电动汽车归为非电动汽车用户，记作用户g∈G，令交通网所有类型用户集合为U={E，G}；而对应用户的出行需求起点-终点（origindestination，O-D）对集合记为(i，j)∈Wu=We⋃Wg（代表用户从节点i去往节点j），其中，Wu、We、Wg分别为用户u、e、g的需求O-D 对集合；用户相应需求O-D 对w的可选择出行路径集合记作Kw。

1.1 考虑用户出行成本预算的交通流模型

在实际的城市交通网中，用户出行的需求很大程度受到出行所需成本的影响。当交通路况受到车流量影响而产生拥堵时，用户个体的出行成本也随之升高；考虑对于部分受出行成本影响的出行需求，当出行成本高于用户所能接受的最大预算时，用户将改变或放弃出行计划，进而使得交通网整体的出行需求产生改变。为了有效刻画上述现象，本节引入用户出行成本预算的概念，即通过出行成本预算来反映用户出行成本对于出行计划的影响［17］，从而为实际用户的出行提供参考。出行成本预算的具体定义如下:

定义1:交通网络中任意需求O-D 对w之间，用户u能够容忍的最大出行成本为用户出行成本预算，记作Cu，w。

根据定义1 可知，出行成本预算Cu，w反映了用户最高所能接受的出行成本，即当用户u在需求O-D 对w之间的所有行驶路径中最小的出行成本cu，w，min超过Cu，w时，用户则放弃出行计划。

为方便建模，考虑在有向图GT(NT，A)的基础上进行拓展，定义包含虚拟路径的交通网络为GT(NT，A ⋃Z)，其中，Z=Ze⋃Zg表示虚拟路径的集合，Ze为用户e的虚拟路径集合，Zg为用户g的虚拟路径集合。同时，在不失模型有效性的前提下，对模型进行简化处理，将交通网络中所有用户出行视为受出行成本预算影响的变化需求。在所有需求O-D 对之间建立一条虚拟的通行路径以表征出行成本预算的影响机理，具体示意图如图1 所示。

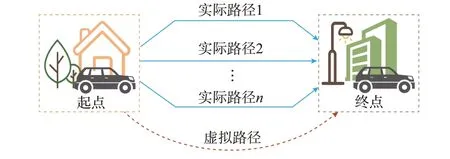
图1 含虚拟路径的交通网Fig.1 Transportation network with virtual paths

定义用户u在需求O-D 对w之间虚拟路径上的流量为Hu，w，其大小与用户u在需求O-D 对w之间选择不出行的用户数量相对应，虚拟路径流量越大，意味着选择不出行的用户数量越多。根据文献［17］，出行成本预算Cu，w可通过下述美国联邦公路局（Bureau of Public Road，BPR）函数进行表示:

式中:w0为用户出行时间的成本折算系数；Tu，w和yu，w分别为用户u关于需求O-D 对w的出行时间预算和虚拟路径容量参数。

从式（1）可以看出，用户对应需求O-D 对的不出行数量越多，用户的出行成本预算越高。yu，w较小的情况下，用户的出行预算受不出行用户数量影响显著；反之，则不显著。而用户的出行时间预算Tu，w大小由用户需求O-D 对距离的远近所决定，同时，由于用户e存在充电需求，其出行预算中应涵盖充电费用，Tu，w表达式为:

式中:κ为修正系数；|Kw|为路径集合Kw的总段数；为无车流情况下自由行驶路段a所花费的时间；λCS为无车流量情况下充电站的充电价格；EB为用户的固定充电量；和为路段a与实际路径k的关联矩阵元素。用户e的可行路径k经过路段a则有=1；反之=0。用户g同理。

基于上述框架，建立考虑用户出行成本预算的交通流数学模型如下。

1）路段行驶时间函数

式中:ta(xa)为通行路段a所花费的时间；xa为路段a的车流量；ya为路段a的容量；R 为函数的形状参数；yn为充电站n的极限容量。

2）路段流量

式中:he，k和hg，k分别为用户e和g选择可行路径k的车流量。

3）流量等式约束

式中:hu，k∈{he，k，hg，k}；qu，w为用户u关于需求O-D 对w的总出行需求。

4）个体出行成本函数

式中:ca(xa)为通行路段a所需成本；γa，n为路段a与充电站n的耦合关系系数（γa，n=1 代表路段a经过充电站n，反之不经过）；λn为充电站n的充电价格；cu，k为用户u选择路径k所需要的总出行成本。

式（3）为一般路段和充电路段所需的时间成本函数，分别用BPR 函数以及排队充电函数进行描述；式（4）为路段流量和路径流量之间的关系；式（5）表示出行用户和不出行用户数量总和应等于用户总出行需求量；式（6）表示所有路段的流量必须非负；式（7）和式（8）描述了用户实际出行成本同交通网流量之间的函数关系。

1.2 考虑出行成本预算的静态用户均衡描述

根据Wardrop 原理，交通网中用户以自身出发成本最低选择出行方案，网络最终将达到用户均衡的状态［8］。在用户均衡状态下，任意需求对之间的所有被使用路径的行驶费用相等，且为所有路径中的行驶费用最小值。需指出，对于需求对之间虚拟路径中的用户而言，同样满足用户均衡的原则。综上，含电动汽车的交通用户均衡状态可通过如下逻辑关系式进行描述:

式（9）和式（10）表示用户将选择成本最小的路径出行，且用户无法通过改变此时的出行路径来减少自身的出行费用；式（11）和式（12）代表当实际最小出行费用等于出行成本预算时，用户会选择虚拟路径（即采取不出行策略），进而体现用户出行成本预算对于实际网络静态用户均衡的影响。为了方便建模求解，将上述逻辑表达式等价为如下非线性互补约束:

对于式（13）和式（14），当第k条路径的出行流量大于0 时，则该条路径k的出行费用与最小出行费用相等，而路径k的用户流量等于0 时，路径k的成本一定大于或等于最小出行费用，符合用户均衡的定义；式（15）和式（16）则说明网络的最小出行成本不得超过用户的出行成本预算，当虚拟路径流量大于0 时，实际出行成本等于用户出行成本预算，结果符合上述逻辑表达式。

然而，非线性互补约束难以直接求解，通常的解法是引入二进制变量进行松弛［7］，但这一方法并不适合于大规模均衡问题的求解。鉴于变分不等式与非线性互补约束有着良好的等价性，处理过程无须引入整数变量，故将非线性互补约束式（13）—式（16）转化为变分不等式问题［13］:

式中:H=[hu，k，Hu，w]T为实际路段以及虚拟路段的用户出行车流分布；F(H*，λ)=[cu，k，Cu，w]T为用户的出行成本以及出行成本预算；λ为用户出行的充电价格；H*代表最终用户均衡状态下的用户出行车流分布；ΩT={H|DH=Q，H∈R+}为用户出行车流分布H的可行域集合，其中，D和Q为常系数矩阵，R+为正实数域。

2 含充电负荷的配电网模型

为描述辐射状配电网模型，可通过有向图GE(N，L)进行表示，其中L 为线路的集合，N 为配电网节点集合。考虑到电力网与交通网通过电动汽车充电站节点进行耦合，且充电站节点集合NCS属于电力网节点，即NCS⊂N，交通流量xa与充电负荷之间存在的线性映射关系可表示为如下等式约束:

为了满足发电要求，配电网的任意节点须满足功率潮流平衡的等式约束:

对于辐射状配电网的任意线路两点之间的电压降约束，可通过下列等式进行描述:

线路功率、电压以及电流三者之间的关系为含二次线性项的等式约束，为了方便求解处理，将原来的等式约束松弛为二阶锥不等式约束:

考虑到电网的安全稳定运行、电能质量要求以及配电网发电机组的发电能力，配电网的相关变量还需满足以下约束条件:

最终，含充电负荷的配电网最优潮流整体模型可表述为如下优化问题:

式中:αn、βn、β0均为发电成本系数为平衡节点注入的有功功率；π为功率削减惩罚系数。

在配电网中，一般采用节点边际价格（locational marginal price，LMP）作为充电站售电价格［6，14］，其等价为有功平衡方程式（20）的拉格朗日对偶变量λ。

为了方便说明，将二阶锥松弛后的最优潮流模型写为如下矩阵形式:

式中:A、B、Γ、E、Λ、Φ、G、K均为常系数矩阵；ξ、φ、τ为常数向量；X=[]为决策变量，代表了配电网的发电策略，(λ，X)构成了电力-交通网络综合定价策略集。

3 充电定价策略的OPVIC 模型

配电网有功平衡约束中包含电动汽车充电负荷，其由交通用户均衡子问题界定。结合上文，可将充电站充电定价问题写成如下紧凑形式:

上述问题是OPVIC［18-19］，该问题存在非凸非线性约束，难以通过一般求解器进行求解。为此，本文采用变量分离的思想，将电网的发电定价策略(λ，X)和用户车流分布H分为两组变量。在电网充电价格λ以及发电策略给定的情况下，将问题式（30）转化为关于变量H的变分不等式问题进行求解；在用户车流分布H给定情况下，问题为带有二阶锥不等式约束的优化问题，可通过一般求解器进行求解。故针对上述OPVIC，本章设计如下交替迭代算法进行求解。

1）算法1:OPVIC 交替迭代算法

步骤1:初始化。设置电网发电定价策略(λ(0)，X(0))，记录迭代次数d=0 并开始迭代。

步骤2:求解考虑出行成本预算的交通网用户均衡问题。在给定电网发电定价策略(λ(d)，X(d))的情 况 下，通过算法 2 求解变分不等式VI{F(H，λ(d))，ΩT}，输出求得的用户车流分布H(d+1)。

步骤3:获得充电站最优充电定价策略。在给定交通网用户车流分布H(d+1)的情况下，根据节点充电负荷需求，求解配电网最优潮流问题，输出充电站电价λ(d+1)。

考虑到实际求解电力-交通网络充电站定价问题中，存在交通用户出行时间横跨多个电力系统调度周期的情况，可根据跨越的调度周期，对充电负荷的时空分布进行划分。然后，执行算法步骤3，输出对应调度周期内的各个充电站的最优充电价格，将充电价格提供给对应时段下途经该充电站进行充电的用户。通过上述改进方案，便可解决实际运用中用户出行横跨多个电网调度周期的问题。限于本文篇幅和侧重点，仅从理论上对方案的有效性进行说明。

由于优化问题所涉及变量均为连续变量且有界，根据布劳威尔不动点定理［20］可知，算法1 具有收敛性，且存在至少一个解。

需指出，步骤2 在电网定价策略给定的情况下求解考虑出行成本预算的交通网用户均衡问题，其涉及了变分不等式问题式（17）的计算。根据文献［21］，采用如下外梯度算法求解变分不等式问题，可获得交通网络的有效均衡解。

2）算法2:外梯度算法

步骤1:选定初始迭代点H(0)∈ΩT，选择每次迭代步长0 ＜α＜1，记初始迭代次数η=0。

步骤2:根据充电站给出的充电价格λ(d+1)，计算此时的F(H(η))，获得在可行域ΩT上的预测投影点

需指出的是，算法1 和算法2 中的ε1和ε2均为算 法 的 迭 代 收 敛 误 差 ；PΩT(H(η))=代表在可行域ΩT中进行投影，寻找最靠近H(η)的解。通过选取合适的迭代步长α，使得外梯度函数F(H) 在可行域ΩT满足Lipschitz 连续时，算法具有收敛性，即其中，L为常数，满足0 ＜L＜1。

4 算例分析

4.1 算例介绍

本文采用SCE 56 节点的配电网与TN 28 节点的交通网作为测试算例，对电网充电站充电定价策略的有效性进行分析，其结构如图2 所示。模型中涉及的仿真所需参数和仿真结果均已共享。仿真求解流程基于MALTAB+YALMIP 平台，算法中涉及的优化问题均通过调用Gurobi 求解器进行求解。

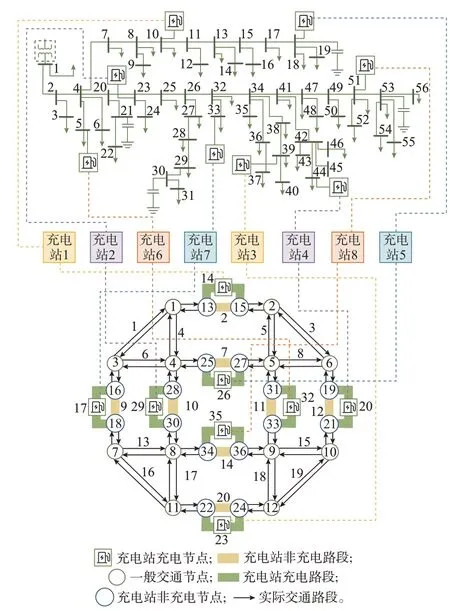
图2 电力-交通耦合网络测试算例Fig.2 Test case of power-transportation coupling network

4.2 求解分析

为验证算法1 求解OPVIC 的有效性，图3 给出了算法求解的误差收敛曲线图。从图3 可知，OPVIC 交替迭代算法在迭代至5 次时，迭代误差ε1满足了1×10-5的收敛要求；但由于路段流量持续变化，充电站价格发生了较大的变化波动。直到12 次迭代后，迭代误差ε1降低至1×10-5以下，在之后迭代过程中，误差无明显变化。因此，在算法迭代至12 次后，电力-交通耦合网络达到了用户均衡状态，此时充电站充电价格为最优定价策略。

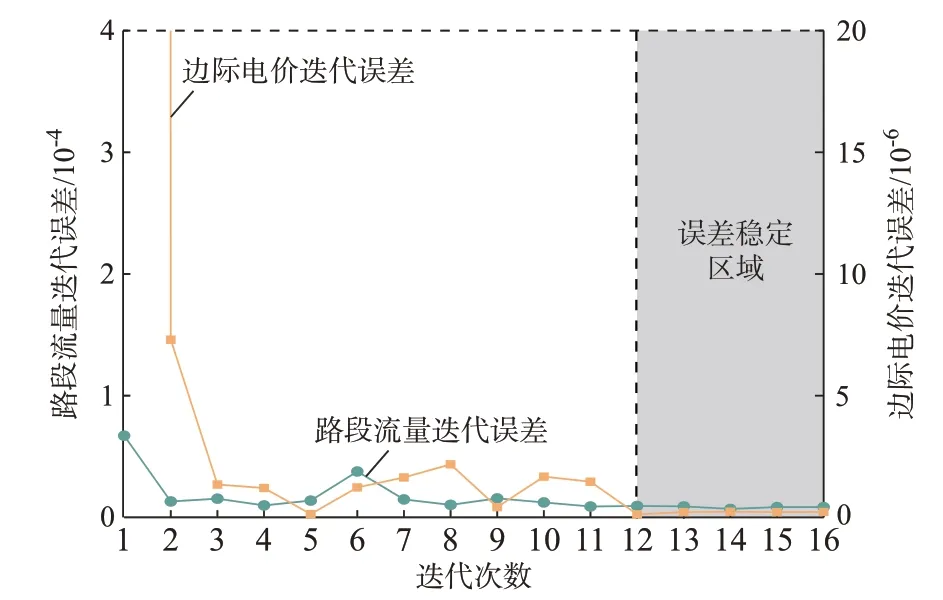
图3 交替迭代算法误差曲线Fig.3 Error curves of alternating iteration algorithm

为测试外梯度算法能否对变分不等式问题进行有效求解，图4 给出了交替迭代算法第1 次迭代时外梯度算法的误差曲线图。从图4 的迭代结果中可以看出，算法2（内层）第1 次迭代时间最长，收敛时间需300 s（误差降低至10-5以下），而后续迭代时间迅速降低，到达第3 次时，算法收敛只花费了3.34 s，并在之后迭代时间无较大变化。出现上述结果的主要原因是一开始的初始迭代点H(0)相距最优解H*(λ(0))较远，因而搜寻当前最优解所需的时间较长；而后续外梯度算法选取上一次迭代所求得的解H*(λ(d))作为初始点，迭代前后充电站价格策略λ(d)→λ(d+1)的变化较小。因此，初始迭代点H*(λ(d))与此时最优解H*(λ(d+1))的距离较近，从而使得算法能够在较短的时间内收敛。综上所述，外梯度算法的求解效率与选取初始迭代点和最优解之间的距离有关。通过选取合适的初始迭代点，外梯度算法能够在合理的时间内对变分不等式问题进行有效求解。

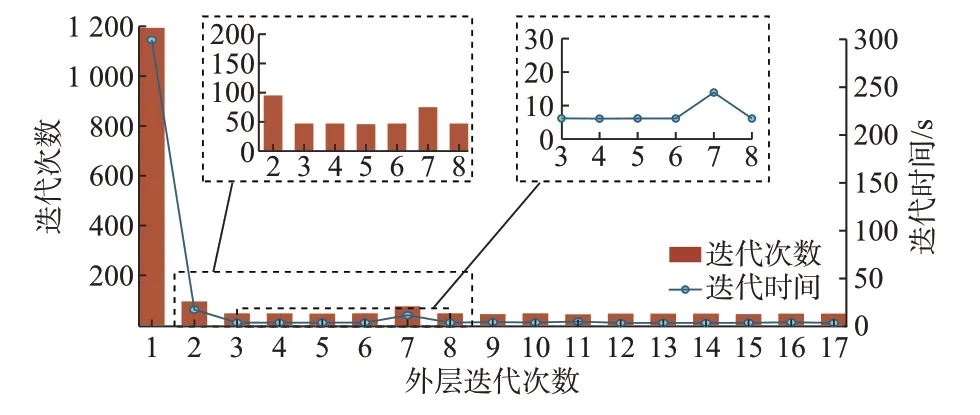
图4 外梯度算法迭代误差曲线Fig.4 Iteration error curve of external gradient algorithm

4.3 仿真结果分析

为验证交通网是否达到用户均衡状态，图5 给出了不同类型用户的部分需求O-D 对的路径流量以及对应的出行成本，并将实际出行成本与预算绘制折线进行对比。图中:黄色代表实际路径流量及对应出行成本，绿色为虚拟路径流量以及出行成本预算。仿真结果表明，流量不为0 路径的出行成本为所有可行路径中的最小值，并与用户出行成本预算相等；而对于出行成本不为最小值的路径，路段流量均为0。仿真结果符合1.2 节所定义的考虑用户出行成本预算的交通网用户均衡状态。

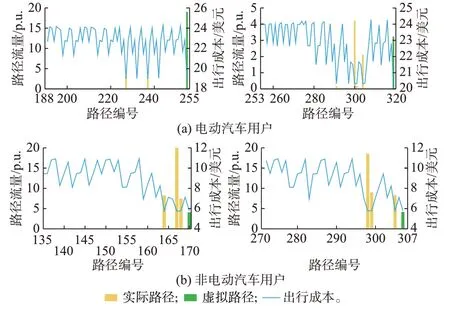
图5 部分需求O-D 对路径流量与出行成本分布Fig.5 Distribution of path traffic flow and travel costs for some demand O-D pairs

为体现出行成本预算对于交通网络用户均衡状态的影响，本文选取不同的修正系数κ=0.8～1.0，对用户出行时间预算Tu，w进行修正，并给出不同出行成本预算下的电力-交通网络实际出行需求数量对比结果，如图6 所示。

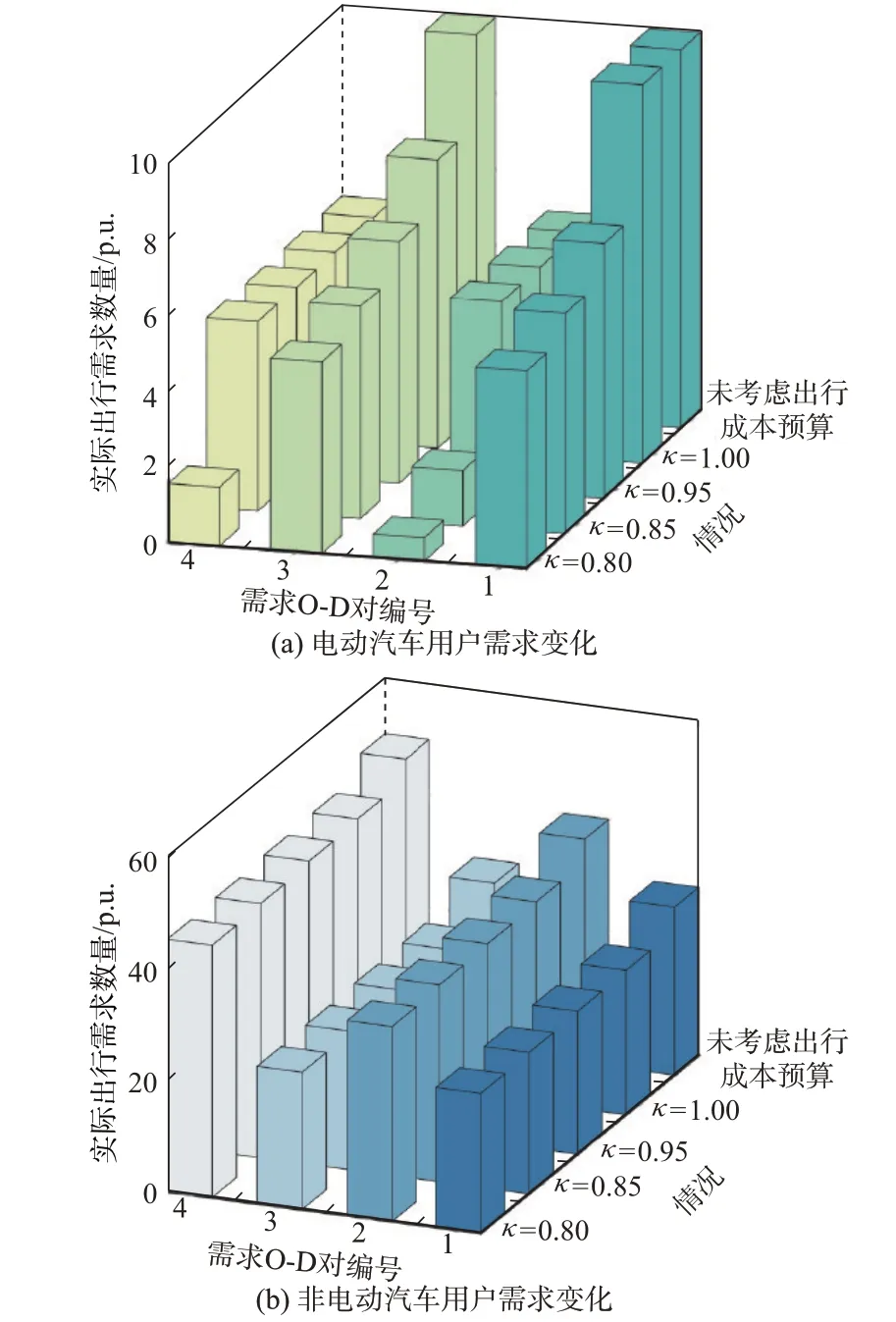
图6 不同修正系数下的实际出行需求数量对比Fig.6 Comparison of actual traveling demand numbers with different correction factors

由图6（a）和（b）的结果可知:1）当预算成本较大时（κ=1.00 时），考虑出行成本预算与未考虑出行成本预算方案的出行需求数量相同；2）在预算成本较小的情况下，随κ的减少，电动汽车用户部分需求O-D 对的出行需求显著降低，而非电动汽车用户的出行需求降低均不明显。该现象的主要原因是电动汽车用户存在额外充电成本，使得出行成本远大于非电动汽车用户，用户预算低的情况下，交通的拥堵更容易使得电动汽车用户选择不出行。上述结果表明，电动汽车和非电动汽车用户的实际出行数量均受出行成本预算的大小影响，且出行需求大致与预算成本成正比。因此，合理估计用户的出行成本预算能够更有效预测交通网中的用户实际出行需求量，进而预测各个充电站的充电负荷，对充电站定价具有重要意义。

表1 给出了各个充电站在不同修正系数κ下的充电价格。其中，未考虑出行成本预算方案的充电价格高于考虑出行成本预算方案。修正系数κ越小，充电站的充电价格则越高。该现象主要原因为考虑出行成本预算后，出行需求有所减少，充电站的充电负荷低于未考虑出行成本预算的情况，充电价格相对降低。通过考虑出行成本预算，能够更好地对充电站的实际充电负荷进行预测，从而使得充电站能够在确保配电网经济稳定运行的同时，提供更低的充电价格，满足出行用户的充电需求。

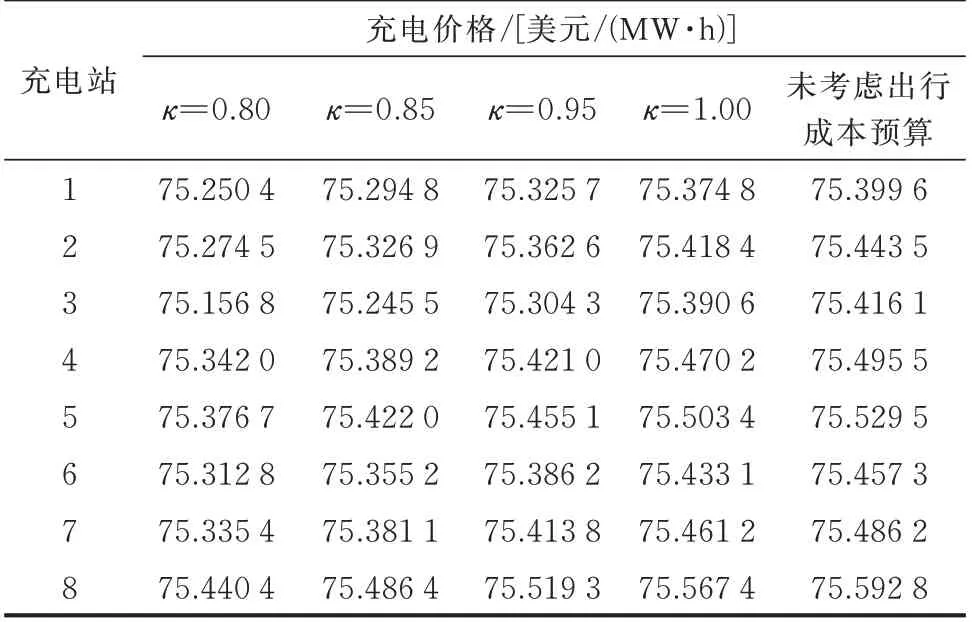
表1 充电价格对比Table 1 Comparison of charging prices

4.4 灵敏度分析

本文所考虑的用户出行成本预算的函数表达式中，修正系数κ和虚拟路径容量参数yu，w分别反映了用户的出行意愿和需求受出行数量的影响程度。为分析参数对于模型结果的影响程度，仿真采用不同的模型参数，对充电站充电定价问题进行求解。

图7 给出了不同参数下，充电站充电价格的变化规律。从结果中可以看出，修正系数κ越大，虚拟路径容量参数越小，则充电站的电价越大。其中，电价受到修正系数κ的影响较为显著。κ=0.85～0.95的范围内，修正系数κ与电价呈近似线性正相关的关系，而后修正系数超过0.95 后，充电站电价的上升速率减缓，这是由于在κ=0.95～1.0 情况下，用户拥有充足的出行成本预算，使得实际出行需求与充电站负荷的变化不明显，进而导致充电价格没有出现较大波动。相比于修正系数，充电站电价对于不同的虚拟路径容量参数的灵敏度较低。在κ=0.8～0.9 的范围内，充电站与虚拟路径容量负相关；而在κ=0.9～1.0 时，对于不同的虚拟路径容量，充电站电价基本无变化。其主要原因是出行需求较小时，虚拟路径容量小的情况下，用户拥有更多的出行成本预算，充电需求相比虚拟路径容量大的情况更多，充电价格也因此增加较为明显；当出行需求较大时，虚拟路径流量少，虚拟路径容量的大小对于用户出行成本预算影响相对较弱，充电价格变化不明显。通过灵敏度分析的结果可以得知:充电站的充电价格受到用户的出行意愿影响较大；在实际路段出行数量少的情况下，充电价格还会受到出行数量的影响，定价策略有所改变。

5 结语

本文充分考虑用户出行成本预算对出行决策的影响，建立了考虑用户出行成本预算的电力-交通耦合网络充电站充电定价模型。相比于传统的电力-交通网络定价模型，本文充分考虑用户出行成本预算对充电定价策略的影响，能够更准确地对实际网络中的充电站负荷进行预测。

本文基于变分不等式框架，将充电站定价问题转化归纳为OPVIC，并根据OPVIC 的特性，设计OPVIC 交替迭代算法以及外梯度算法对问题进行求解。仿真采用56 节点配电网和28 节点交通网的耦合网络进行测试，仿真结果表明所提交替迭代算法能够对系统级别的耦合网络中充电站定价问题进行快速求解。同时，仿真设置了多个方案进行结果对比，发现考虑出行成本预算的定价方案相较于传统模型方案，能够为用户提供更低的充电价格，降低用户充电成本。最后，通过不同参数下的仿真结果可知，用户出行成本预算对于充电价格的制定结果影响显著，验证了考虑用户出行成本预算对充电站定价的必要性。

未来的工作将基于本文所提的考虑用户出行成本预算的充电定价策略，研究用户出行需求随时间变化的动态响应。引入微分变分不等式，结合本文所提算法，对时域空间下的动态电力交通网用户均衡模型进行分析，求解获得电力-交通耦合网络中充电站的实时动态定价策略，进而更为精确地调控充电负荷分布，进一步提高电网经济性。

本文算例仿真相关参数和仿真结果已共享，可在本刊网站支撑数据处下载(http://www.aeps-info.com/aeps/article/abstract/20230628010）。