考虑负荷空间均衡和充电站合作博弈的快速充电定价机制

2024-04-22戴朝华叶圣永

电力系统自动化 2024年7期

杨帅，戴朝华，郭爱，叶圣永

（1.西南交通大学电气工程学院，四川省成都市 611756；2.国网四川省电力公司经济技术研究院，四川省成都市 610041）

0 引言

电动汽车（electric vehicle，EV）作为交通领域可持续发展的重要组成部分，已被认为是解决能源危机和温室气体排放的重要发展方向［1］。为了能在短时间内为用户提供充电服务，满足用户出行的快速充电需求，快速充电技术正在逐渐取代传统的慢速充电模式，而由于用户出行的不确定性，规模化快速充电负荷呈现出更为明显的冲击性。时间维度上，会加剧电网高峰时段供电压力，给安全稳定配电造成极大的消极作用；空间维度上，会造成用户充电拥堵和电网调度困难等问题［1-7］。

围绕减轻规模化充电负荷入网影响的问题，目前已经取得了一些研究成果。文献［8-11］提出以电网分时电价为基础，网侧最小化电网负荷方差，EV用户侧最小化用电成本，建立充电调度模型，实现了对电网基础负荷曲线削峰填谷的效果。文献［12］考虑了充电负荷时空特性和用户出行时间成本，以最小化用户充电成本为目标实现负荷曲线削峰填谷，并为车主提供最佳的充电站选择和充电策略。文献［13］考虑用户充电过程中“电网-充电站-用户”多个主体，用双层博弈模型描述充电站竞价过程和用户最佳充电策略选择过程，能够有效平衡EV 用户、充电站和配电网三者之间的经济利益。

基于传统分时电价和用户特性得到的引导策略对电网的充电负荷有一定的均衡作用，证明通过改变用户充电成本实现有序充电引导是可行的。但对于采用快速充电的用户，其理想充电时间安排较为紧凑，使得上述基于分时电价的引导策略并不适用。另一方面，传统分时电价促使用户错峰用电，是在时间维度上的充电引导，不能解决充电负荷在空间上的不均衡性。为此，文献［14］提出了配电网供电电压偏差指标，建立用户充电位置决策模型，通过合理改变充电站电价引导EV 用户在空间上有序充电。文献［15］基于源-荷互动思想提出考虑负荷均衡和弹性响应的快速充电定价策略，能够有效提升充电桩利用率以及配电网负荷时空均衡性。文献［16］提出综合考虑时间、充电费用、路况、荷电情况等因素的充电决策优化模型，为EV 用户提供最佳充电时段及最低充电成本的决策，可缓解充电拥堵，改善路-电耦合网络整体运行状况。

当前快速充电站（fast charging station，FCS）多数为第三方承包商，且同一区域内可含有多个充电站承包商，上述研究虽然考虑了EV 用户、充电站运营商和配电网三者之间的耦合关系，但是对于不同充电站承包商之间的相互作用缺乏考虑。通过改变电价均衡空间维度的快速充电负荷，即使可以保证运营商总体效益不变，也可能会导致部分充电站效益增加而其他充电站效益减少的情况。因此，目前缺乏有效定价策略来统筹区域内所有第三方充电站，在满足电网、各充电站和EV 用户多方利益的前提下实现快速充电负荷的有序引导。

综上所述，本文提出考虑负荷空间均衡和充电站合作博弈的快速充电动态定价机制。首先，利用路网模型和速度-流量模型对EV 时空快速充电负荷进行建模。其次，考虑排队时间、距离、价格、吸引度等因素对用户选择快速充电站时的影响，以计及用户偏好的充电站选择模型模拟用户的充电站决策行为。然后，提出合作博弈模式下的快速充电站动态定价策略，以配电网运营商（distribution system operator，DSO）统筹区域内快速充电站组成合作联盟，使快速充电站之间以节点负荷均衡性为目标，通过充电电价进行博弈，得到各快速充电站营业电价，并通过Shapley 值法对合作联盟剩余收益进行分配。最后，以成都某地区为例进行仿真，采用负荷空间分布的均衡性、用户排队时间和充电站收益为指标，验证所提快速充电站定价引导策略的有效性。

1 合作博弈模式下快速充电站动态定价策略框架

电力体制化改革背景下，鼓励第三方运营商单独承包充电站，向电网购电再提供给EV 用户并收取服务费，DSO 负责配电网侧的运营规划，可与各充电站进行友好互动，促进需求侧主体之间的良性竞争，提高电网与用户之间电能交易的效率［17］。DSO 辖区内同时包含有若干第三方快速充电站和慢速充电站，快速充电站建造成本较高，充电速度较快，位于商业区、办公区等公共区域，为有需要充电的EV 用户提供充电服务，而慢速充电站充电功率较小，所需充电时间较长，主要位于各小区停车场，为小区用户在未出行时间提供充电服务，每个慢速充电站服务用户较为固定。

本文所提快速充电站动态定价机制，针对快速充电站节点负荷均衡性进行研究，建立在DSO 与快速充电站信息实时交互的基础上，由DSO 负责每个充电站服务费的定价。具体框架如图1 所示，各快速充电站将每个充电桩的使用情况、当前时段被占用的充电桩预计空出时间等信息上传至DSO［18］。EV 用户通过DSO 提供的用户交互界面发出充电需求，并设置充电偏好，如绕路意愿大于排队意愿，或偏重价格因素。DSO 统计同一时段内用户充电需求信息（地点、荷电状态（state of charge，SOC）和偏好等）后，以节点负荷均衡为目标、快速充电站为参与者、电价为策略展开合作博弈，博弈达到均衡后向用户提供充电站选择结果和向充电站下发充电服务费的定价。

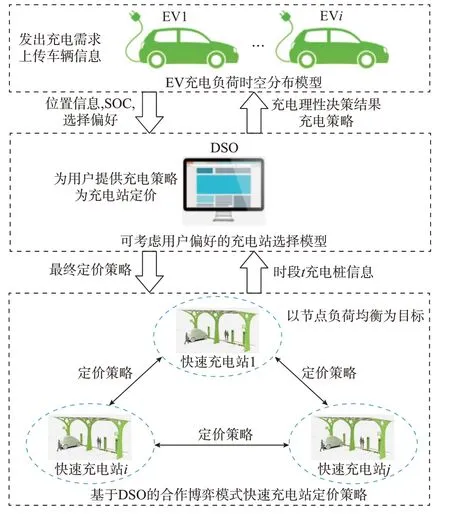
图1 动态定价机制框架Fig.1 Framework of dynamic pricing mechanism

对所提动态定价机制做出如下假设:

1）参加调度的用户完全信任由DSO 交互界面给出的充电决策建议，所提充电站选择模型会做出最利于用户的充电选择决策；

2）DSO 以不会低于单独营业时的收益为条件与充电站签订合约，保证充电桩与DSO 实时通信，上传充电桩使用状态和下发博弈后的充电定价；

3）认为DSO 具有担负整个博弈计算过程的能力，统筹快速充电站实现的负荷空间均衡，且决定各充电站的充电定价。

DSO 令拥堵充电站与其周围若干充电站组成合作联盟，区域内各合作联盟独立定价，对合作联盟区域内用户提供博弈定价结果。对区域外的用户提供初始分时电价，合作联盟外边缘充电站的用户不会因为合作联盟内充电站价格降低而改变充电站选择，造成出现新的负荷不均衡情况。DSO 不会干涉用户的参与意愿，只是通过降低愿意绕路用户的充电成本和不愿意绕路用户的排队时间来吸引尽可能多的用户参与调度。

2 EV 充电负荷时空分布模型

2.1 动态路-网模型

城市交通路网模型可表示为G={O，P，D，B}，其中，O={1，2，…，Nd}为路网节点集合，Nd为节点总数；P={(m，n)}为路网中的支路集合，道路等级分为主干道和次干道；B为道路饱和度集合，B中元素bm，n，t表示t时刻路段(m，n)之间的道路饱和度；D为道路邻接矩阵。当路段(m，n)∈P，D内元素Dm，n=Dn，m=lm，n，其中，lm，n为节点m到n的距离；当m=n，Dm，n=Dn，m=0；否则，Dm，n=Dn，m=inf，表示两节点并不直接相连，需要经过其他节点才能实现通勤。

2.2 出行起讫点(origin-destination，OD)矩阵

OD 分析法主要是描述用户在已知出发地的情况下，根据OD 矩阵转移概率随机生成目的地［19］。滴滴平台盖亚开发数据计划公布了成都地区2016年11 月的用户订单轨迹数据，包含每个订单的出发时刻、结束时刻、出发地经纬度和目的地经纬度，滴滴乘客的出行需求概率应该与私人EV 用户出行概率大致相同，可用滴滴乘客出行概率刻画EV 用户转移概率。

将用户日常活跃区域分为5 个功能区:住宅区（residence）、文化教育区（science，education，culture）、工作区（companies）、商业娱乐区（business，entertainment）、日常事务区（medical，sports，social）、其他。将一天分为7 个时间段:07:00—09:00（上班高峰期）、09:00—12:00（工作高峰期）、12:00—14:00（午休）、14:00—17:00（工作高峰期）、17:00—19:00（下班高峰期）、19:00—23:00（晚间娱乐）、23:00—次日07:00（夜间休息）。

提取盖亚开发数据中某一天的所有订单数据共24 388 条，将订单数据输入高德开放平台进行一一逆地理编码，提取结果中订单起始地与目的地所属的功能区。对逆地理编码得到的数据进行初步处理，剔除不属于5 个功能区的目的地与出发地（高速路口等地），将所有数据按照时段进行分类，再按照出发地进行分类，即可计算时段t从功能区qa出发去往某个功能区qb的概率gqa，qb，t，如式（1）所示。

式中:Bqa，qb，t为时段t内出发地为功能区qa、目的地为功能区qb的行程数；Nq为划分的功能区数。

2.3 速度-流量模型

已知EV 用户出行起点与终点，需要再通过模拟具体行程得到EV 耗电量和所花时间。汽车道路行驶速度与道路容量和道路饱和度有关，引入速度-流量模型［20］（见式（2）），刻画EV 行驶过程中的实时速度。

式中:vm，n，t为时段t内车辆在路段(m，n)上的行驶速度；v0，m，n为路段的零流速度；ε、μ、σ为自适应系数，与路段的道路等级有关。道路饱和度bm，n，t为此时段道路流量与道路通行能力的比值。本文道路数据参考文献［21］。

2.4 Floyd 最短路径算法

出行过程中EV 用户通常选择行驶起点与终点之间最近的一条道路，利用Floyd 算法［22］将所有可行路径进行距离比较，可得到最短路径。行程花费时间ΔT和所耗电量ΔSc分别如式（3）和式（4）所示。

式中:dm，n为地点m和n之间的距离；m，n∈Ω，其中，Ω为由出发地到目的地的最短路径需要经过的节点集合；NΩ为所需要经过的节点总数；ΔTk为第k段路程需要花费的时间，每个路段行驶时间之和为行驶总时间；dm，n，min为由地点m到地点n的最短距离；ΔE为单位千米耗电量。

3 计及用户偏好的充电站选择决策模型

充电站选择决策模型研究中，大部分趋向于选择路程最少或者时间成本最低的充电站进行充电，现实情况中不同的消费者对于充电站的喜好可能会不一样，同一消费者在不同的时间对于充电站的需求侧重也可能不同。综合考虑EV 用户产生充电需求后对充电站选择时的影响因素所建立的模型更加贴合实际［23］。本文首先分析影响EV 用户充电决策因素，通过改进Huff 模型整合多重因素模拟EV 用户对于充电站的理性决策行为。

3.1 EV 用户充电站选择行为分析

用户在出行过程中充电的流程如附录A 图A1所示，在t1时刻做出充电决策后行驶至充电站，时间为t2，花费时间t2-t1，影响t2-t1大小的是充电站的距离和行驶所需时间。到达充电站后，若没有空位，需在排队时间结束后开始充电至车主理想SOC，花费时间t4-t2，则充电站的排队时间和充电桩充电功率是需要考虑的因素，与其相关的是充电站的规模和充电桩利用率。另外，EV 充电过程用户需要处于等待状态，若充电站或其附近有相应休息室，商业广场等设施则会加大对EV 用户的吸引度。最后，充电成本也是用户关心的重要问题，充电站对于服务费的定价也会影响EV 用户的充电站决策行为。

3.2 EV 用户充电站选择决策模型

Huff 模型利用商圈吸引力大小描述用户对于商圈的选择概率大小［24］。本文定义充电站对于用户吸引力效用U受到充电站空闲率、距离和价格等因素的影响，用户可根据自身需求对影响因素设置不同权重进行充电站的选择决策。用Ui，j，t表示时段t内充电站j对于用户i的吸引力效用，基于权重的Huff 模型如式（5）所示。

式中:α、β、γ、η为权重系数。

Ds，i，j为用户i到充电站j的距离比例，距离越近，Ds，i，j越大，如式（6）所示。

式中:Nc为车辆耗电至用户最低理想SOC 内能到达的充电站数量。

Tp，j，t为时段t在充电站j充电需要等待的时间比例，表达式见式（7）。相关研究表明，相比于排队充电，用户更趋向于绕路充电，充电排队时间的增加会使用户对于充电站的选择概率大幅度减小。

式中:Tpai，j，t为用户在时段t选择充电站j需要经过的排队时间。

Pr，j，t为时段t内充电站j的价格比例，与充电站所收取的服务费有关，表达式如下:

式中:Se，j，t为时段t充电站j所收取的服务费，单位为元/（kW·h）。

Ax，j为充电站j的额外吸引力指标，取决于充电站附近的配套设施，有无休息室、商场等。在DSO统一调控的智能用电市场中，可以通过不断地采集用户数据得到贴合实际情况的权重系数α、β、γ、η。若对于不同因素的偏好，例如，时间较为空余更看重价格，或者不愿绕路更看重距离，都可以根据DSO交互界面给出的建议调整偏好因素的权重系数，利用选择决策模型做出考虑用户意愿的理性决策。

在对EV 用户充电站选择理性决策时，应满足以下约束条件。

1）充电等待时间约束

排队时间内用户需要等待挪车，时间不能空出，所以用户对于较长排队时间忍耐性较小，对用户充电行为理性决策后选择的充电站j排队时间应小于排队时间约束Tpai，max。排队时间过长且选择不愿绕路选项的用户可能会放弃充电或选择回家充电，可描述如下:

2）剩余里程约束

当EV 发出充电需求后，需要在剩余SOC 到达用户最低理想SOC 值（取0.1）之前能到达的充电站之间进行选择，所以用户到达可选充电站时SOC 应大于0.1，如式（10）所示:

式中:S0为用户发出充电需求时的剩余SOC；Eev为EV 电池容量。

4 合作博弈模式下的快速充电动态定价策略

某些地段人流量较高，充电高峰期充电站的排队时间较久，部分用户会选择绕路充电，其余不愿绕路充电的用户可能会选择缩短行程，取消充电，导致充电负荷空间不均衡较高和用户充电满意度较低。通过DSO 协调统筹区域内充电站组成合作联盟，令不同利益主体的充电站相互合作以引导EV 用户空间有序充电，可提高充电站收益和用户充电满意度。合作博弈为具有约束和合作协议的博弈，假设集体和个体理性，个体之间组成联盟获得额外的利益，使个体能得到比单独营业时更多的利益［25］。

充电站选择决策模型中，充电电价可作为需求侧响应的引导变量，以DSO 作为快速充电站充电服务费的统一调控平台，通过协作调节充电站之间的快速充电价格，可以吸引更多用户在充电站拥堵的时候选择绕路充电，避免充电需求较多的节点充电站出现拥堵情况，容纳更多的用户充电，从而增加充电站整体营业利润，提高充电站利用率。

4.1 合作联盟

以参与人、策略集、目标函数和特征函数为所提合作博弈模型的4 个要素，定义为(F，Pe，f1，u)，其中，F为合作博弈参与者集合；Pe为策略集；f1为联盟目标函数，是联盟中个体合作博弈的目标；u为联盟特征函数，是合作联盟博弈后的收益。合作博弈相关定义如下。

1）具体的参与者与策略集

参与者集合F={F1，F2，…，FNc}，其中，F1表示序号为 1 的充电站；策略集Pe={Pe，1，Pe，2，…，Pe，Nc}，其中，Pe，1={Pe，1，1，Pe，1，2，…，Pe，1，t，…，Pe，1，96}表示充电站1 一天的定价策略，Pe，1，t表示时段t充电站1 的快速充电定价。本文以15 min 为一个时间段，一天分为96 个时间段，DSO负责合作博弈计算，可以支撑以15 min 为一次的调整周期。

2）合作联盟稳定约束

保持合作联盟的稳定需要满足以下两个条件:

a）集体理性:合作联盟整体收益必须大于每个充电站单独经营时所获得的利益之和，即

式中:uj为合作联盟里的充电站j获得的总收益；xj为充电站j单独营业时获得的收益。

b）个体理性:合作联盟中的每个个体所分配到的收益必须大于单独经营所获得的个体利益，即

4.2 目标函数及特征函数

额外的利益促使充电站之间达成合作联盟，由DSO 统筹下的合作博弈直接目标是提升区域内充电站的节点的负荷均衡度，以此提高充电站利用率均衡度，缓解充电站排队情况，为更多的用户提供充电服务。

4.2.1 目标函数和约束条件

式中:f1，t为时段t内充电站充电负荷集合ls，t的方差；ls，1，t表示编号为1 的充电站在时间段t提供给EV 用户的电能；var（·）表示求方差函数。

DSO 在对充电站定价时应满足以下约束条件:

1）充电电价约束

电价的改变应处于合理范围之内，如式（14）所示。

式中:Pe，j，t为时段t充电站j的充电定价；Pe，min为充电站定价最低值，为保证充电的运行成本，最低值应高于DSO 发布的电能分时电价；Pe，max为充电站定价最高值。

2）用户平均充电成本约束

电价改变过程中，用户平均充电成本不能发生太大变化，成本过小会使合作联盟因为收益降低而无法保持稳定，成本过高影响用户充电响应度。具体约束如下:

式中:Ce，t为时段t内EV 用户的平均充电成本；Ce，min为用户最低充电成本；Ce，max为用户最高充电成本。本文设置用户平均充电成本不超过合作博弈之前的1.05。

3）总售电量约束

DSO 对各充电站电价进行调整，应使充电站容纳更多的EV 用户进行充电。因此，调节后DSO 所提供的总电量应不低于调整前，有

式中:Ej、E′j分别为充电电价调整前后充电站j一天内提供的充电电量。

4.2.2 特征函数

合作博弈的核心涉及合作联盟额外收益的分配，定义个体收益函数即特征函数如下:

式中:vs为合作联盟总体收益；Pg，j，t为电网在时段t售电给充电站j的电价；Ep，j，t为充电站j在时段t接待的充电负荷。

4.3 基于Shapley 值的合作增益分配模型

Shapley 值分配法［26］以某利益主体（本文中为充电站）对联盟的边际贡献价值作为增益分配的衡量标准。为综合衡量某利益主体在各种加入位次下的边际贡献价值，构造分配权重系数Ws，j（见式（18）），该系数表示主体j加入联盟应分配到的边际增益占比［27］。

式中:|S|表示包含个体j的联盟S的个体数；N为整个合作联盟所包含个体数，即充电站数量Nc；(|S|-1)!表示某主体最后一个加入联盟S的所有排列数目；(N-|S|)!表示某主体第1 个加入联盟S的所有排列数目。

按照上述权重对边际收益u(S)-u(S-{i})进行分配，得到每个个体在合作博弈之后所得的收益:

式中:S-{i}为联盟集合S除去个体j后的剩余联盟；Xj为个体j所获收益，将基于Shapley 值分配所得个体收益作为合作联盟个体最终收益。

Shapley 值利益分配强调个体参加合作与未参加合作所产生的收益区别。博弈过程中，拥堵充电站抬高自身电价，将过多或超过容量的用户引流到空闲充电站；空闲充电站在这个过程中降低自身电价，提供空闲充电桩为通过博弈引流的用户服务。这样，保证了两种充电站在此过程中的贡献值，使得在分配时两种充电站的合作能保证获得不小于单独营业时的收益。

4.4 合作博弈模式下的快速充电站动态定价策略实现步骤

合作博弈均衡存在性证明见附录B，以时段t内各快速充电站定价过程为例说明所提动态定价策略的具体实现步骤，如图2 所示。

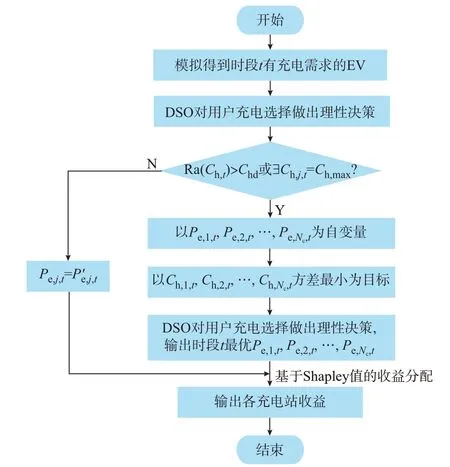
图2 快速充电定价机制流程图Fig.2 Flow chart of fast charging pricing mechanism

步骤1:模拟得到时段t需要充电的EV 集合，EV 通过DSO 交互界面提交剩余SOC、所处位置和充电选择偏好，由DSO 为每位EV 做出初始充电决策。

步骤2:统计时段t每个充电站的充电桩占用数Ch，t={Ch，1，t，Ch，2，t，…，Ch，Nc，t}，其中，Ch，1，t表示时段t充电站1 内充电站的占用数。若所有充电站的充电桩均有空闲（占用数小于充电桩总数Ch，max），且充电站充电桩占用数集合的极差Ra(Ch，t)小于允许值Chd，则以初始分时电价P′e，j，t为充电站电价并结束定价过程；否则，利用本文所提动态定价策略进行定价。

步骤3:DSO 对时段t内各充电站电价展开合作博弈求解，以时段t各充电站的电价为自变量，通过充电决策模型对充电站节点负荷集合的方差展开寻优。

步骤4:博弈达到均衡后得到的时段t各充电站最优电价作为此时段的充电站电价。

步骤5:重复步骤1 至4，完成一天的充电站定价。

步骤6:模拟结束后输出充电站一天的各时段电价，利用Shapley 值法对合作博弈得到的额外收益进行分配。

5 算例分析

5.1 仿真数据

假设中国成都某DSO 控制区域包含5 个快速充电站，1 500 辆日常活动EV，区域结构如图3 所示。图中:快速充电站所属节点为正方形图标，其中，节点3 为风景名胜区，节点14 为某大型广场，人流量较其他节点大。每个节点所属功能区如图3 所示。为使计算变得简便，假设所有EV 车型均为比亚迪海豹标准续航版，电池容量Cp为61.4 kW·h，最大行驶里程Xmax为550 km，快速充电功率设置为60 kW，单位公里耗电量为0.165 （kW·h）/km，充电桩效率设置为0.95，SOC 达到0.3 或者不足以完成下一行程任务时的用户发出充电需求。

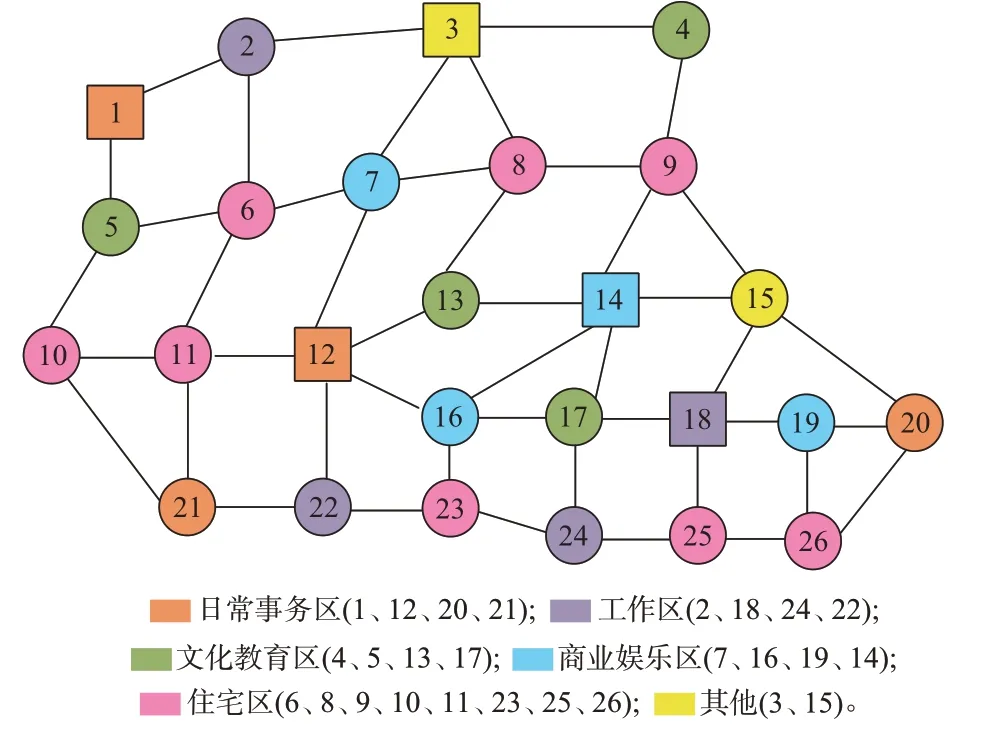
图3 区域节点示意图Fig.3 Schematic diagram of regional nodes

EV 出行时刻、出发SOC 等参数通过概率函数随机拟合得到，出行时刻符合N（7.25，0.92）的正态分布，回家时刻符合N（19.55，2.06）的正态分布，出发SOC 符合U（0.5～0.95）的均匀分布。设置充电期望SOC 为0.95，默认一天中EV 最多完成一次充电行为，则当EV 出现充电需求后，记录其SOC、当前时刻和当前位置后停止模拟，进入充电站选择步骤。

充电站初始电价以DSO 根据基础负荷曲线发布的分时电价为基础，可对EV 充电起到时间维度上的引导作用，成都某地区一天内的分时电价如表1 所示。

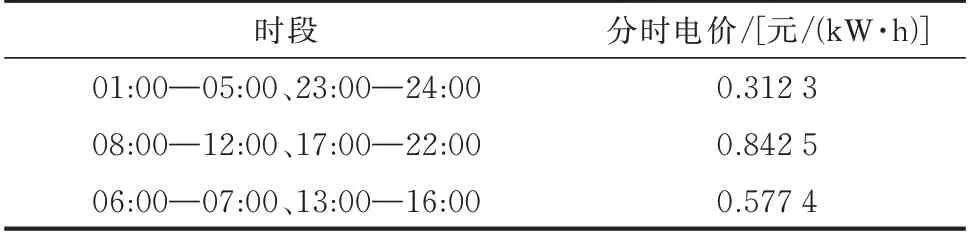
表1 成都某地区分时电价Table 1 Time-of-use electricity price for a region in Chengdu, China

设置充电站选择模型的权重系数初值α、β、γ、η分别为0.25、0.25、0.2、0.3。为验证本文所提充电站定价策略的有效性，设置如下2 种仿真场景用以对比。

场景1（引导前）:充电站作为独立的个体运营。模拟EV 用户一天行程，在产生充电需求后仅基于分时电价对充电行为进行引导。当用户不愿意绕路充电而选择的充电站排队时间又较长，可能会放弃充电。

场景2（引导后）:运用所提合作博弈模式下的快速充电动态定价策略对EV 进行充电引导。

5.2 仿真结果

5.2.1 充电站选择模型参数选取

距离、排队时间、吸引度和价格在充电站选择模型中的权重系数α、β、γ、η无法脱离实际给出确定的取值，可以证明的是权重系数的合理变动不会影响本文所提快速充电引导策略的有效性。根据不同用户偏好设置4 种权重系数组合以对比说明。如表2所示，组合1 为初值，组合2 所有用户对于距离因素的权重减小到0.15，用户对于绕路充电意愿加强；组合3 所有用户对于排队时间权重减小到0.15，用户对于排队时间忍耐度增加；组合4 所有用户对于价格差价权重减小到0.2，用户对于价格差价吸引力减小。

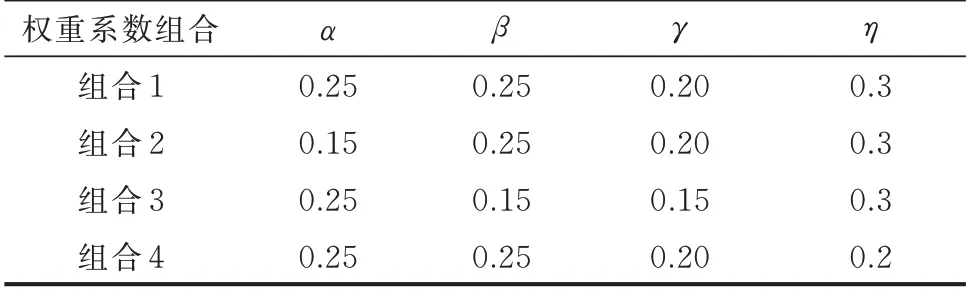
表2 4 种权重系数组合Table 2 Four combinations of weighting coefficients

充电站日接待量的不同可以反映充电负荷的均衡度，4 种不同偏好的权重系数组合下的各充电站日接待量如附录A 图A2 所示，引导后4 种权重系数组合下的充电站接待量波动性均大大减小。具体地，用充电站日接待量集合的方差刻画充电负荷空间引导效果，如图4 所示，4 种权重系数组合下的充电站日接待量集合方差在引导后（红色折线）均跌落至引导前（蓝色折线）的11%以内，说明所提定价策略在不同用户偏好情境下都能实现有序充电引导。

4 种权重系数组合下充电站与用户收益如附录A 表A1 所示，引导后EV 人均成本均处于约束范围之内，在用户有侧重偏好的情况下，引导后的EV 人均成本比组合1 高，说明对于存在用户偏好的情况需要更大的价格差价来实现有序引导。

5.2.2 EV 用户满意度对比

3.1 节中分析了用户出行中的快速充电流程，认为充电成本、充电时间和排队时间是影响用户充电满意度的重要因素，本算例中各充电站的充电功率相同，为EV 提供充电服务所需时间没有差异。

1）成本对比

如表3 所示，充电站达成合作联盟后整体获利增加356.6 元，为未引导时的4.1%，主要来自引导后的充电站吸引了之前由于排队时间长、绕路远而放弃充电的用户（电量低于阈值但足以支撑到达下一目的地），在EV 用户人均基本成本不变的情况下增加了电网和充电站的收益。

表3 快速充电站与EV 用户收益Table 3 Benefits of fast charging stations and EV users

基于Shapley 值对合作联盟收益进行分配，如图5 所示，合作联盟收益的分配占比取决于个体对于合作联盟的边际贡献，合作联盟的剩余收益来源于为更多的用户提供了充电服务。在未进行充电引导时，这些用户选择了人流量较多的充电站2 和4进行充电，由于需要等待的时间过长并且不愿意绕路而暂缓了充电计划。当充电站2 和4 与其余比较空余的充电站协同调节充电服务费时，拥堵区域充电站价格上升而其他区域充电站价格下降，这会增加上述用户绕路充电的意愿，所以充电站2 和4 对于合作联盟的边际贡献大于其他充电站，占比65.9%。合作联盟个体收益增加3.4%～5.6%，满足个体理性和集体理性2 个稳定条件，证明本文所提合作博弈模式的充电站定价策略能有效增加充电站收益。

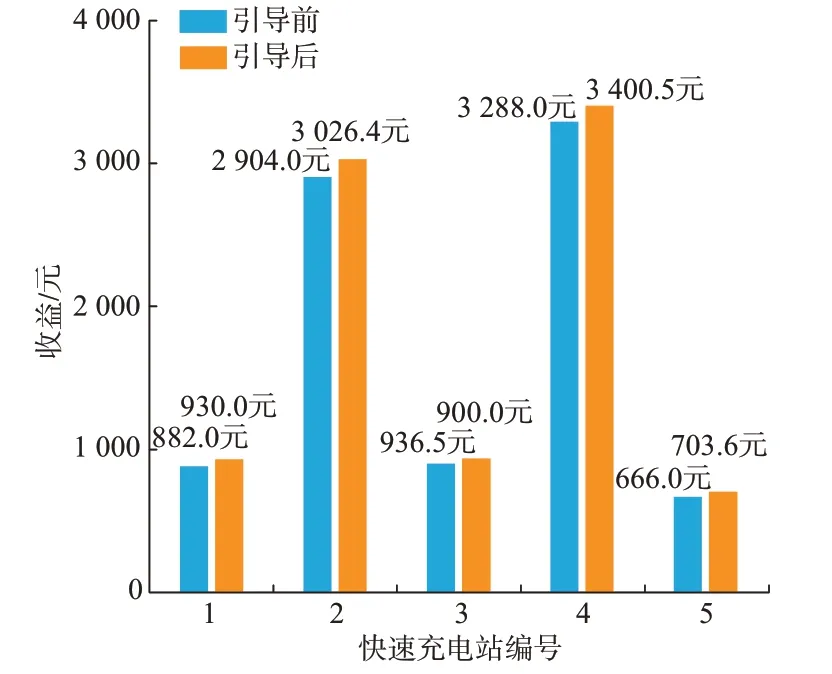
图5 基于Shapley 值的收益分配Fig.5 Distribution of benefits based on Shapley values

2）排队时间对比

充电站平均排队时间指所有选择该充电站的用户排队时间的均值。如图6 所示，图6（a）为充电站2各时段内的用户平均排队时间对比，需要排队的时间集中在10:00—14:00 之间，平均排队时间为8.50 min，充电引导后充电站2 的平均排队时间减少到1.56 min，拥堵情况得到缓解。图6（b）为充电站4各时段内的用户平均排队时间对比，充电站4 位于商业中心地区，人流量较大，09:00—17:00 都需要排队，平均排队时间为10.13 min，充电引导后平均排队时间为1.58 min，大部分时间段不再需要排队。从图中可以得出，部分用户通过改进Huff 模型权衡对价格、排队时间、绕路距离的综合考虑，选择了价格更低，充电桩空闲位置更多的充电站。

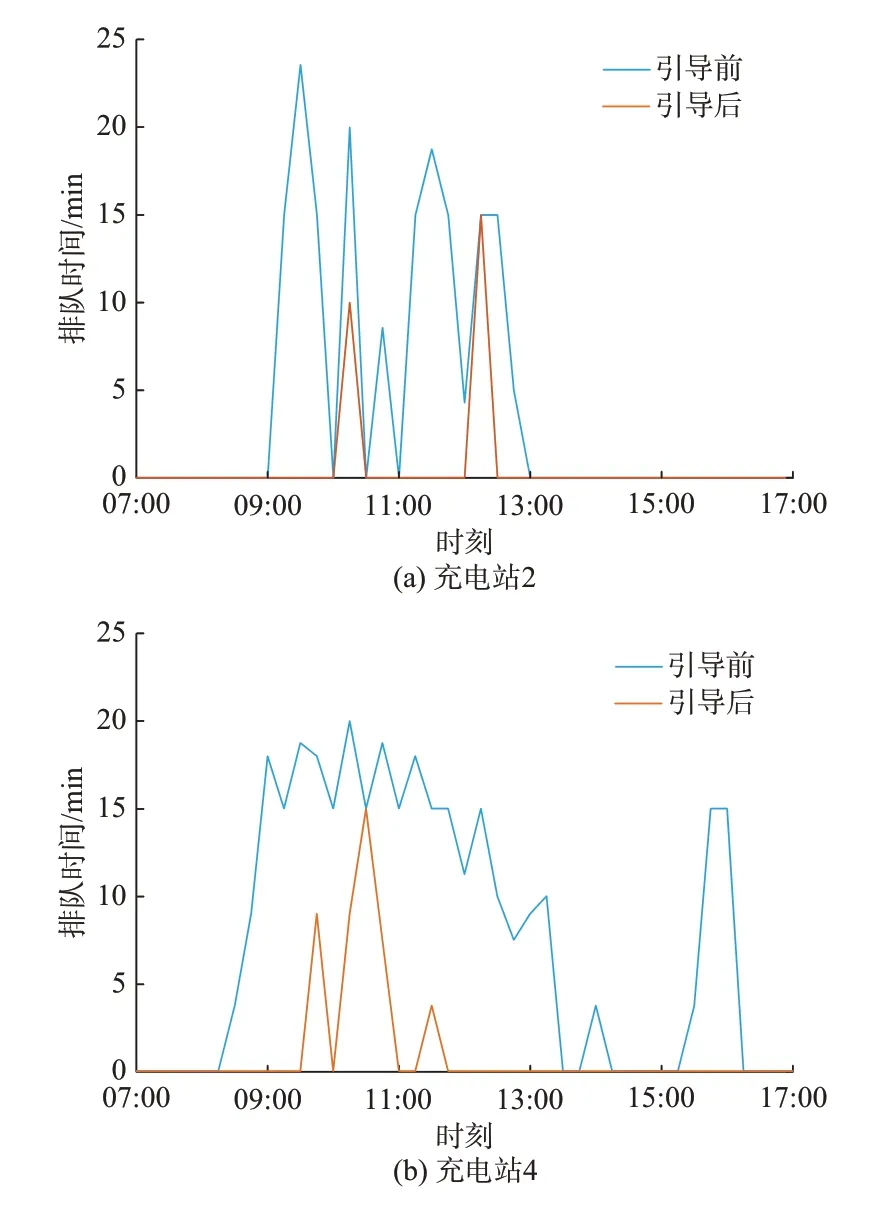
图6 平均排队时间对比Fig.6 Comparison of average queuing time

峰值时刻各充电站定价结果如附录A 图A3 所示，红色和黑色直线分别为充电站2、4 在该时段未引导的充电站定价，由于地段不同，充电站2、4 初始定价较其余充电站高。从图A3 可以看出，人流量峰值时段充电站2、4 电能定价均高于初始电价，充电站1、3、5 大部分时段处于定价初值之下，在电价允许范围内，通过电价差引导了用户空间有序充电，实现负荷空间均衡。

应用所提快速充电定价机制使用户充电成本基本不变的情况下，减小了用户的排队时间。其中，部分用户在价格引导下选择绕路，到邻近空闲充电站进行充电，降低了充电成本和排队时间，其余用户用略微增加的充电成本换取在不需要绕路的情况下减少充电排队时间。对比于引导前的充电拥堵情况，两种用户充电满意度都得到提高。

5.2.3 网侧负荷均衡性对比

为具体研究所提的动态定价机制对于快速充电负荷空间均衡的引导效果，定义时段t充电桩利用率均衡度δt，其为研究时段内充电桩的利用率方差，如式（20）所示。

式中:φj，t为充电站利用率；φav，t为充电站平均利用率。

如图7 所示，引导后的充电桩利用率方差大幅度减小。每时段的平均利用率方差从7.73 降到了1.02，降幅86.8%。

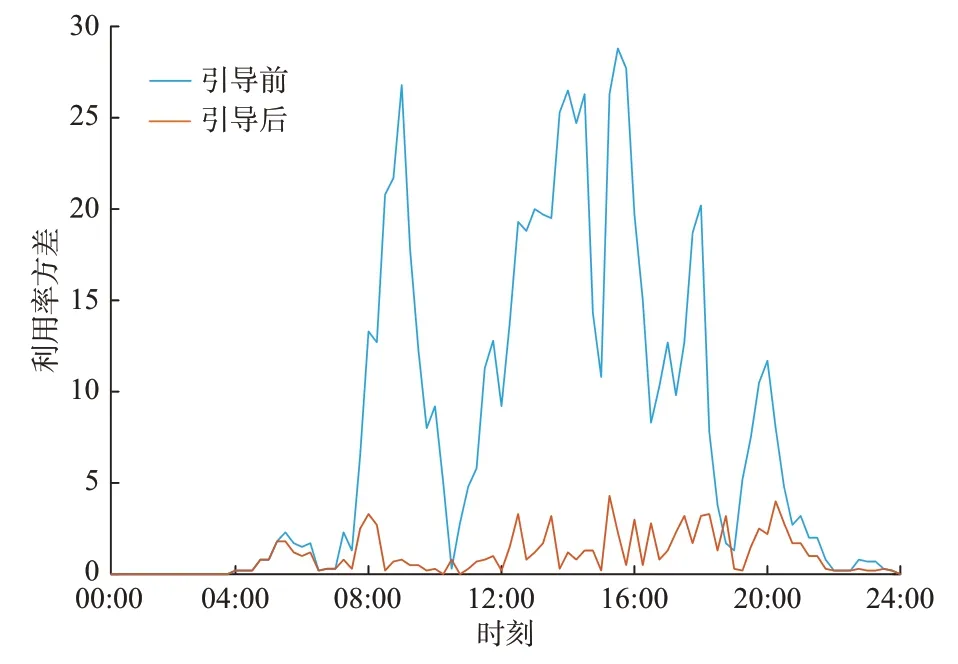
图7 充电引导前后利用率方差对比Fig.7 Comparison of utilization rate variance before and after charging guidance

附录A 图A4 给出了引导前、后的快速充电负荷时空分布对比。可以看出，电价引导前，同一时段不同节点的快速充电负荷有明显波动，引导后，节点之间负荷波动性明显降低，负荷分布更加均衡。负荷高峰期充电站2 和4 的满载运行时段减小，可降低配电网的运行压力，提高电能质量。表明本文所提充电站定价策略有效引导了快速充电负荷的空间分布，提升了充电桩利用率和配电网负荷的均衡性。