基于动态哈夫模型及双边匹配的电动汽车充电引导策略

2024-04-22王建祥李玉璟聂晓波向文旭

电力系统自动化 2024年7期

苏粟，王建祥，王磊，李玉璟，聂晓波，向文旭

（1.北京交通大学电气工程学院，北京市 100044；2.中交机电工程局有限公司，北京市 100012）

0 引言

随着全球环保意识的提升，电动汽车作为一种低碳、环保的交通工具得到广泛重视和推广［1-2］。随着中国电动汽车数量迅速增长［3］，作为新基建七大领域之一的充电桩也在加快建设［4］。当前，很多车主会选择在在线地图软件和充电桩应用程序等充电站聚合平台寻找附近的公共充电站进行充电，但在充电站选择时具有随机性和盲目性［5］。同时，对上述应用程序的调研发现，现有充电站推荐平台缺乏个性化充电站推荐策略，且由于推荐过程缺乏用户反馈，充电桩推荐难以确保供需一一对应［6］，这在降低用户充电服务体验的同时，导致充电站收益下降。因此，充电站聚合平台需要对用户进行充电引导。

众多学者从不同角度对电动汽车充电引导问题进行了研究。文献［7］为实现对路网、充电站和电网的协同优化，提出基于第三代前景理论的电动汽车充电引导策略。文献［8］以充电负荷均衡、交通流量均衡、用户成本低为目标，提出一种计及用户出行成本的主从博弈模型对用户进行充电引导。文献［9］建立了包含车辆、充电站、交通网和电网的多目标优化模型，能够在毫秒级响应充电请求的同时有效缩短电动汽车充电时间。然而，以上引导方式均是对所有用户的无差别引导，没有充分考虑不同用户的个性化需求。

文献［10］提出一种基于冲突消解的链式充电桩推荐算法，综合考虑了电动汽车用户在距离、充电时间和充电价格等多方面的需求，以及充电桩利用率的均衡需求。文献［11］综合考虑了电动汽车用户和充电站双方的利益，以电动汽车用户能耗小、充电费用低、充电站等待时长短为目标，提出了充电桩预约和最佳路径推荐方法。文献［12］以充电站利用率均衡和电动汽车用户出行时长最短为目标，提出了为预约用户合理分配充电时段的策略，以降低用户的出行时长和成本。然而，上述研究中的模型建立和算例分析中缺少实测数据，降低了所提策略的准确性、稳定性和可解释性。

文献［13-14］均使用双边匹配策略对用户进行充电引导，能够保证用户与被推荐充电桩一一对应。其中，文献［13］考虑用户对距离、行驶时长和充电费用的偏好程度，兼顾用户和充电站双方利益，使用双边匹配策略为用户提供充电引导。文献［14］在文献［13］的基础上，更全面地考虑了匹配双方的偏好值，且对用户进行分类，满足用户个性化需求。然而，文献［14］求解双边匹配模型所使用的改进延迟接受算法具有偏向性，对先选方（用户）更有利，且偏向性难以调整，灵活性差；算法的时间复杂度高，耗时近似与充电桩数的平方成正比，难以适用于大规模充电网络；此外，虽然每一轮次的匹配结果具有稳定性，但因一天中需要匹配多次，而各匹配轮次相互影响，匹配结果不再具备稳定性，整体匹配结果也并非全局最优。

为解决上述问题，本文提出了动态哈夫模型与双边匹配相结合的电动汽车充电引导策略。首先，获取了研究区域内各充电站客流数据和用户的充电记录数据，并进行了大数据挖掘，以分析用户充电站选择偏好和充电行为特征。然后，根据各充电站的吸引力及用户前往各充电站所需的行驶时间，通过动态哈夫模型确定各充电站被访问的概率，并生成不同区域的充电站推荐列表，每经过一定时间间隔或充电站推荐列表中出现无可用充电桩的充电站时，更新推荐列表。最后，结合前景理论和双边匹配策略，以电动汽车用户和充电站双方的满意度最大化为目标，提出了电动汽车-充电站双边匹配策略。

1 电动汽车用户群体充电行为分析

1.1 数据源及数据处理

本文通过在线地图［15-16］获取了中国四川省成都市二环内及邻近区域的公共快速充电站基本信息，并获取了2023 年2 月各充电站不同时段的平均空闲桩位数以计算各站点客流，用以分析电动汽车用户的充电站选择行为。数据的详细描述及处理流程见附录A。

为进一步了解用户的充电需求、充电行为特征及车辆特征，本文获取了区域内某典型快速充电站2022 年9 月至2023 年2 月的3 万余条充电订单数据和300 余万条充电桩详情数据进行数据挖掘。所获取数据不涉及用户隐私，不同用户通过用户唯一标识进行区分。所选充电站的详细信息及数据处理流程见附录B。

1.2 用户充电站选择行为分析

结合充电站基本信息和客流数据，本节分析充电站规模及充电价格对用户充电选择行为的影响。

根据各充电站客流确定各充电站的客流占比，并用百分位数表示各充电站内快速充电桩数在所有充电站中的升序排位。百分位数的计算流程见附录A。不同规模充电站的访问频率如图1（a）所示。结果表明，有约60%的充电行为发生在规模最大的30%的站点，电动汽车用户群体偏好选择大规模充电站。用百分位数表示不同时段各充电站充电价格（含电费、服务费）在所有充电站中的升序排位。结合该时段充电站客流，确定用户选择充电站点的价格百分位数，如图1（b）所示。结果表明，有约75%的充电行为发生在价格最低的50%的站点，电动汽车用户群体偏向选择充电价格低的充电站点。此外，约86%的充电行为发生在免收停车费的充电站，进一步说明了电动汽车用户的价格敏感性。

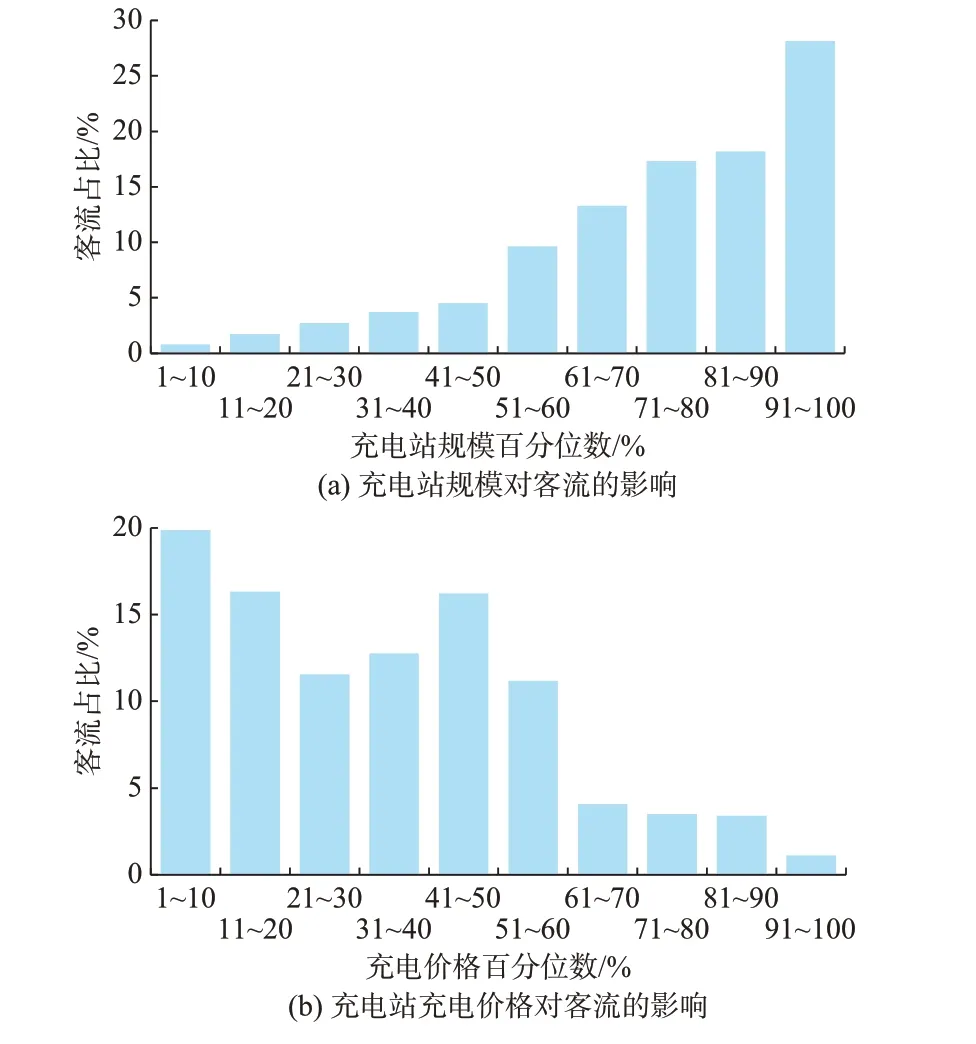
图1 充电站客流分析Fig.1 Analysis of passenger flow at charging stations

充电站评分（满分5 分）对用户的充电站选择也有显著影响，有约82%的充电行为发生在评分4 分及以上的站点。

1.3 用户充电行为描述

为全面描述用户充电行为，本文选取充电起始荷电状态（state of charge，SOC）、充电结束SOC、充电开始时间、充电结束时间、充电量、充电费用作为电动汽车用户充电特征一级标签。一级标签的数据可直接从充电订单数据（见附录B 表B1）中获取，数据分布如附录C 图C1 所示。

选取充电时长、电池容量、平均功率、充电结束后占用时长作为电动汽车用户充电特征二级标签，计算公式如式（1）—式（4）所示，数据分布如附录C图C2 所示。

式中:tc为电动汽车充电持续时间；te为充电结束时间；ts为充电开始时间；Cb为电池容量；Cw为充电量；Se为充电结束时的SOC；Ss为充电开始时的SOC；Pw为充电过程中的平均功率；tz为电动汽车充电结束后占用时长；tl为电动汽车充电结束后离开时间。

2 充电站推荐列表生成

2.1 动态哈夫模型

哈夫模型［17-18］是一种用于预测和分析消费者行为的地理空间模型，其核心思想在于消费者前往各购物中心的概率，取决于购物中心规模对消费者的吸引力及消费者前往购物中心的旅行时间。本文针对充电站选择场景对其进行改进，提出动态哈夫模型。在模型中，充电站吸引力是时变的，可用式（5）表示不同区域电动汽车用户前往各充电站的概率。

2.2 充电站吸引力

用户选择充电站时，主要受充电站规模、充电价格的影响［2］，也不同程度受充电站品牌、配套设施、周边环境等多种因素影响［19］。本文引入充电桩数量、充电价格、停车费用和充电站评分等因素，以描述各充电站吸引力。

不同用户对各因素的偏好具有异质性［2］，但用户群体对各因素的偏好具有一致性。结合1.2 节的充电选择行为分析，同时考虑到各因素的相关性（详见附录A 表A2），本文对充电站吸引力定义如下:

式中:pvc

ks为各权重取值；为充电站各指标在所有充电站中的百分位数（取值0 到100）；τso为模型参数，取两类充电站客流占比为1∶4 时的百分位数作为τso的值；η为各指标的吸引力权重，充电桩数目、充电站评分按升序排列，充电价格按降序排列。收取停车费用时取值为1，否则为η。

式（7）根据充电站特定指标的排位，将充电站分为两类。理论上对各指标进行组合，可将充电站分为16 类，但由于各指标间存在相关性，最终仅存在11 类充电站。其中，数目占比最高的5 类充电站如表1 所示。

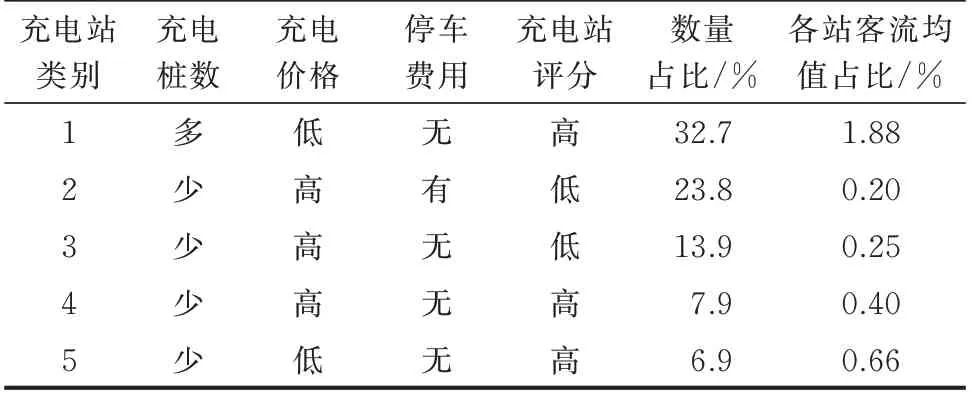
表1 各类充电站数目占比与客流占比Table 1 Percentage of number of charging stations by type and percentage of passenger flow

表1 中，数量占比最高的5 类充电站约占总充电站数的85%，而客流量约占总客流量的78%，具有代表性。由于总是存在2 类充电站仅在某一类指标的类别上存在差异，可以根据各类别充电站客流均值占比的比例确定η的值。对比类别1 和类别5 可知，充电桩数目多的吸引力权重为2.83，同理可知充电价格低、停车费用无、充电站评分高的吸引力权重分别为1.66、1.23、1.63。

2.3 电动汽车用户前往充电站的通行时间

鉴于电动汽车用户在行驶中产生充电需求，且充电站通常在主路附近，本节在建立交通网与充电站网耦合模型的基础上，提出了“主路—小路—充电站”的充电行驶模式，旨在确定用户从所在路段末端节点前往充电站的行驶时间，作为动态哈夫模型中的通行时间。交通网与充电站网络耦合模型如图2所示，可用式（8）、式（9）表示。

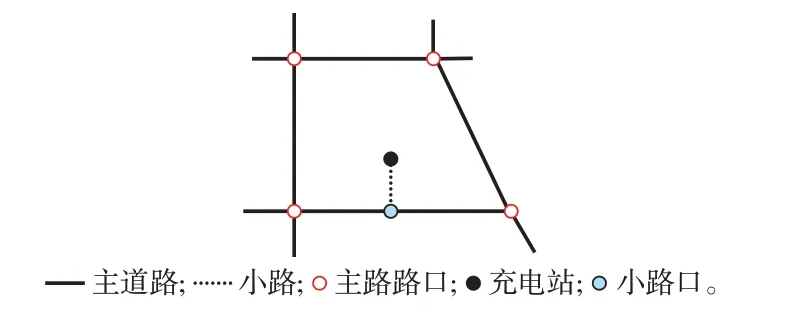
图2 交通网与充电站网络耦合模型示意图Fig.2 Schematic diagram of coupling model of transportation network and charging station network

式中:VBI为主路网中的大路口集合；表示第i个大路口；NBI为大路口个数；VSI为充电站所在小路与主道路连接的小路口集合；表示第j个小路口；NSI为小路口个数；Vcs为充电站集合。

式中:RnIr为连接两个大路口的道路集合；RIr为连接小路口与大路口的道路集合；Rr为当前区域内所有主道路集合；Rsr为连接小路口和充电站的小路集合；表示从路口到路口的有向道路。

通过实时地图接口［16］可以获得用户从所在道路末端节点前往充电站的耗时。但实际上，所获取的时长只是充电行驶模式中主路部分的行驶时长，记为，而不包含小路行驶部分的行驶时长。考虑到实际道路和充电站位置的复杂性，通过式（10）近似计算小路部分的行驶时长，对前往充电站的总耗时进行修正。电动汽车用户从各路网节点前往各充电站节点的充电行驶总时长如式（11）所示。

2.4 充电站推荐列表生成流程

根据充电站密度、充电请求频次以及道路通行速度变化速度等因素，共同确定充电站推荐列表生成时间间隔τg。每经过一个时间间隔τg或充电站推荐列表中出现所有充电桩均被占用的充电站时，针对各路网节点进行一次充电站推荐列表生成。生成流程如下:

1）获取路网和充电站网络数据；

2）依据2.2 节，计算各充电站吸引力；

3）依据2.3 节，计算各路网节点到各充电站的通行时间；

4）依据2.1 节，计算各路网节点被各充电站服务的概率；

5）对于每一个路网节点，取服务概率排名前l的当前有可用充电桩的充电站，生成充电站推荐列表。

3 电动汽车-充电站双边匹配策略

3.1 基于前景理论的偏好量化

当电动汽车用户产生沿途充电需求时，需首先确定其所在道路和行进方向，再获取相应区域的充电站推荐列表，从中选择最适合的充电站进行推荐。根据电动汽车用户群体的历史充电记录数据，得到充电前总时间、充电价格、充电站评分等3 个方面的期望均值，记为期望均值矩阵O=[o1，1，o1，2，o1，3]。根据用户、道路、充电站三方状态得到用户前往推荐列表中各充电站的期望值矩阵M。矩阵中各元素的计算方式如下:

式中:α表示推荐列表中的充电站编号，α=1，2，…，l；mα，1、mα，2、mα，3分别为前往充电站α的总行驶及等待时间、充电价格估计值、充电站评分；tap、tα，s、tα，ar、tα，e、tα，l分别为用户充电请求、到达充电站α、开始充电、结束充电、离开充电站时段；ct，α为t时段电动汽车充电站α的充电量；rt，α为t时段电动汽车充电站α的充电价格单价为向上取整符号；cpk，α为充电站α的每小时停车费用；Sc，α为充电站α的评分。

电动汽车充电站根据用户历史数据，得到对电动汽车用户的充电费用、总占用时长等2 个方面的期望均值，记为期望均值矩阵P=[p1，1，p1，2]。根据当前状态得到对各电动汽车用户的期望值矩阵N，矩阵中各元素的计算方式如下:

式中:nα，1和nα，2分别为电动汽车用户在充电站α的预计充电费用和预计充电桩占用时长。

根据期望值矩阵和期望均值矩阵，得到用户方和充电站方的标准决策偏差矩阵Q及R。标准决策偏差矩阵中各元素的计算方式如下:

交通领域的许多研究表明，人在做出行为决策时表现出有限理性［20］。同样，电动汽车用户在选择充电站时也表现出有限理性［21-22］。本文使用前景理论［23］量化用户不同充电选择行为的价值。用户更关注每次选择的主观价值E(xbias)，而非决策结果的客观价值xbias。前景理论公式中，主观价值的计算方式如下:

式中:xbias为实际值和参照点的差值，代表真实价值；λ1、λ2为风险偏好参数，分别取值为0.88、0.88；λ3为损失规避参数，取值为2.25。

根据前景理论公式、标准决策偏差矩阵Q和R，计算充电站和电动汽车用户双方的价值矩阵，分别记为A、B。矩阵中各元素计算方式如下:

根据电动汽车用户偏好确定对3 个评价指标的权重，并将权重向量转变为标准化向量wu=[]，电动汽车充电站对用户充电费用和占用时长的权重标准化向量为wcs=[]。根据价值矩阵和权重向量，得到综合价值向量A～、B～。向量中各元素计算方式如下:

3.2 双边匹配模型求解

式中:xα为0-1 变量，为0 表示用户不与充电站α匹配，为1 表示用户与充电站α匹配；wsat为引导效果满意度。各约束使得每个电动汽车用户能够匹配到一个电动汽车充电站。

上述模型能够求解出电动汽车用户应前往的最佳充电站。如果用户接受充电引导，则将相应充电站的充电桩分配给用户，并为用户预留充电桩。

模型的具体求解步骤如下:

1）根据用户位置，获取相应区域的充电站推荐列表；

4）用户与推荐列表中的第g个充电站成功匹配，本次匹配的引导效果满意度记为。

4 算例分析

4.1 算例数据

基于第1 章用户充电行为分析，利用所提的充电站推荐列表生成模型及电动汽车-充电站双边匹配策略，搭建含用户-道路-充电站的电动汽车充电仿真系统。

研究区域为中国成都市核心区，区域面积约为62 km2，共含155 个主要道路节点和514 条道路（同一道路不同方向视为2 条），道路总长度为348.88 km。该区域内设有101 个公共快速充电站，共有1 580 个快速充电桩，充电桩覆盖率为25.5个/km2。路网布局及充电站位置见附录A图A2。

根据充电站客流调研数据，将每天充电的电动汽车数目设置为11 500 辆。通过蒙特卡洛抽样的方式，从附录B 表B1 所示的充电订单记录中抽取用户唯一标识，并根据1.3 节方法得到各用户的充电特征标签ts、Ss、Se、Cb、Pw、tz。将充电站推荐列表中的充电站数l设为25，将充电站推荐列表生成时间间隔τg设置为5 min。基于公平原则，将用户方满意度占比wuser设置为0.5；电动汽车用户对各评价指标的权重分布均设置为U（0，1）；充电站对用户充电费用和对用户占用时长的偏好均设置为0.5。

在为接受引导的电动汽车用户预留充电桩的前提下，对比以下策略以验证本文策略的有效性:

策略1:用户不接受引导（即不为用户预留充电桩），并直接前往距离最近的有空闲充电桩的充电站充电；

策略2:用户接受引导，并前往充电站推荐列表中第1 个空闲充电站充电；

本文策略:用户接受引导，并前往充电站推荐列表结合双边匹配策略推荐的充电站充电。

4.2 不同策略的效果评估

4.2.1 引导效果

不同策略的引导效果如表2 所示。由于用户提出充电请求与到达充电站存在时间差，在到达充电站后原本空闲的充电站可能不再具备空闲充电桩。因此，不进行充电引导时，用户的排队等待概率较高，而本文策略则显著降低了用户的排队概率。与其他各策略相比，本文策略显著降低了用户充电总费用，使得用户前往了评分更高的站点，并提升了充电站每小时收益。由于本文策略综合考虑了不同用户对充电前耗时、充电费用、充电站评分等多方面的需求，使得用户的单次充电前总时间比策略2 长了1.342 min，但单次充电总费用（含充电费和停车费）下降了1.903 元。若用户出行的时间成本取较高值35.31 元/h［14］，则与策略2 相比，用户单次充电的总支出下降了3.63%。

表2 不同推荐策略的对比Table 2 Comparison of different recommendation strategies

依据用户的评价指标权重标准化向量，使用K均值聚类将用户分为时间敏感型、价格敏感型及服务敏感型3 类。各类用户的聚类中心分别为［0.53，0.24，0.24］，［0.23，0.51，0.23］，［0.24，0.25，0.53］。

各类用户充电前总时间、充电总费用、充电站评分差异如表3 所示。可以看到，各类用户的个性化需求均得到满足。

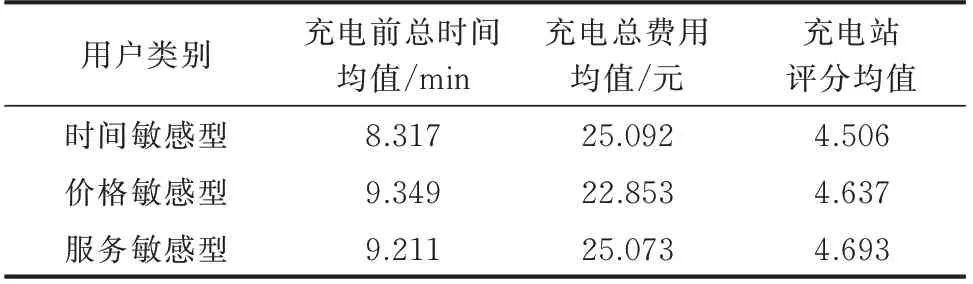
表3 各类用户关键指标分析Table 3 Analysis of key indicators of various users

本文策略不仅使得充电站时间利用率有所提升，而且保证了各充电站功率利用率的均衡。功率利用率定义为充电站当前输出功率与理论最大输出功率的比值。快速充电时，充电速度主要受制于用户车辆。因此，将充电站当前输出功率定义为当前站点接入的车辆的平均充电功率Pw之和。图3 展示了使用本文策略后，一天中各充电站的功率利用率。可以看出，各时段充电站网络的输出功率整体均衡，用户既没有集中在小规模的站点充电，也没有使得大规模站点的充电站功率利用率过低。

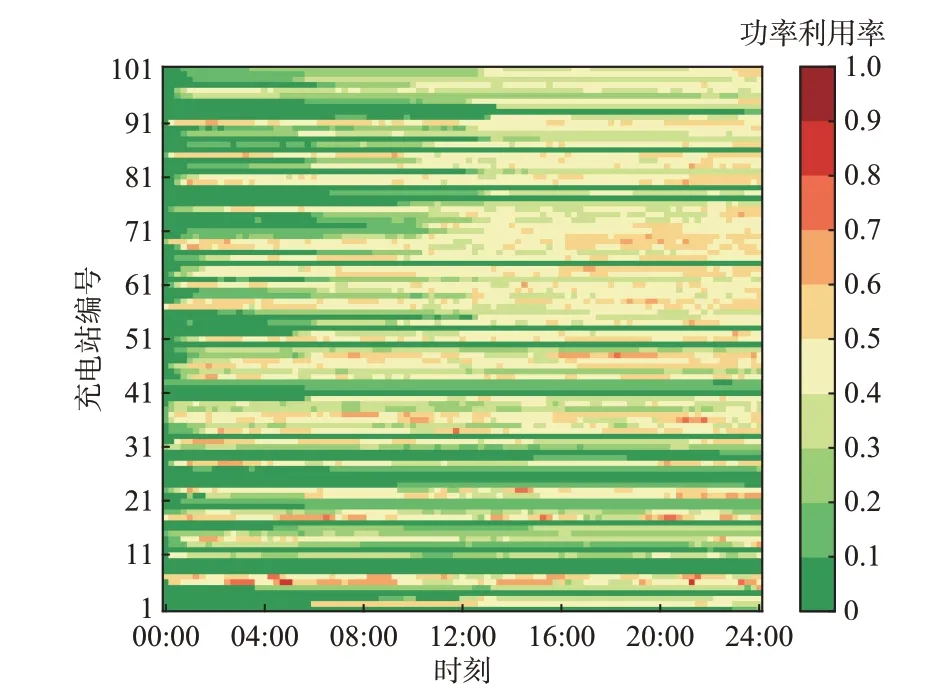
图3 各充电站功率利用率Fig.3 Power utilization rate of each charging station

4.2.2 响应耗时

本节主要分析不同充电请求频次下，引导策略的响应速度。当充电请求分别为1、10、50、100、400次/min 时，引导策略响应一次充电引导的平均耗时分别为0.410、0.347、0.344、0.354、0.340 ms。与文献［9］基于强化学习的引导策略相比，响应时间缩短了约92%。与同样使用双边匹配模型的文献［14］相比，本文匹配模型的算法时间复杂度与充电站推荐列表中的充电站数目成正比，显著优于文献［14］（时间复杂度与充电桩数目的平方成正比）。因此，充电站规模相同时本文模型的匹配耗时更短。

4.3 参数敏感性分析

4.3.1 推荐列表中充电站数目对仿真的影响

充电站推荐列表中，充电站数目l的取值会影响本文策略的推荐效果和推荐系统的响应时长。l值越大，搜索范围越广，越能够找到符合当前用户个体预期的充电站。但是，当前用户的充电站选择改变了充电桩的可用性，影响了后续一段时间内其他用户的充电站选择。因此，增大l值也更容易导致一个更适合未来用户的充电桩被预先分配给当前用户，从而影响整体引导效果的全局最优性。基于公平原则，通过一天中所有充电引导的满意度wsat均值，对整体引导效果进行评估。一天中的整体引导效果与充电站数目关系如图4 所示。

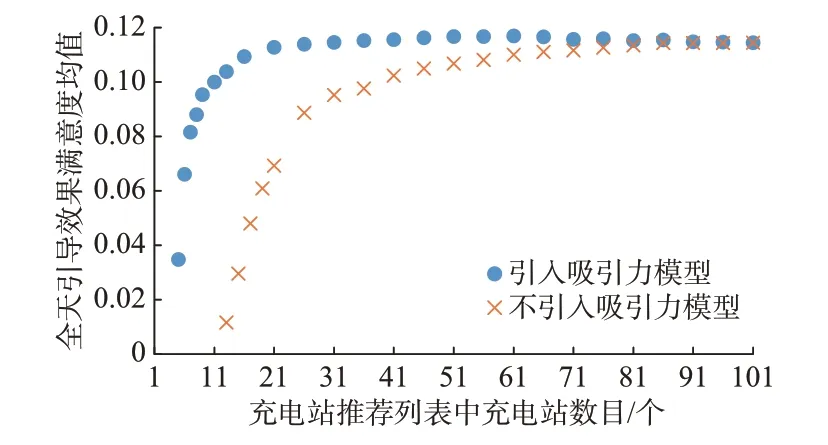
图4 充电站推荐列表中充电站个数对满意度的影响Fig.4 Effect of number of charging stations in the recommended list of charging stations on satisfaction

从图中可以看出，在未引入充电站吸引力模型（各充电站吸引力均为1）时，随着搜索范围的扩大，用户的个性化需求逐渐得到满足。因此，整体引导效果随着推荐列表中充电站数目的增加，先快速增加再缓慢增加；充电站列表中的充电站数目达到91后，再增加充电站数目，整体引导效果才基本不变。引入充电吸引力模型后，在充电站数目达到25 后整体引导效果就基本稳定。原因如下:引入吸引力模型后，综合考虑了充电站吸引力和用户前往充电站的通行时间这2 个指标，使可供匹配的候选充电站的选择更合理。因此，吸引力模型的引入使得在推荐列表中充电站较少时，引导效果优于不引入吸引力模型。引入充电吸引力模型后，在充电站数目达到61 个后，继续增加充电站数目，整体引导效果略有下降，原因如下:由于列表中已有大量较为合理的候选充电站，充电站数目进一步增多对引导效果提升较小；同时，更多的更适合未来用户的充电桩被预先分配给当前用户，造成引导效果陷入局部最优。上述分析同时说明，与匹配前仅考虑距离的充电站预筛选［14］相比，引入吸引力模型对充电站进行预筛选，可以使得整体引导效果更优。

4.3.2 用户方满意度占比对仿真的影响

本节讨论使用本文策略对用户进行引导时，用户方满意度占比wuser的变化对仿真的影响。将wuser取为0.5 时的各指标值设置为基准值（各指标具体值见表2），wuser取不同值时各指标的标幺值如图5所示。

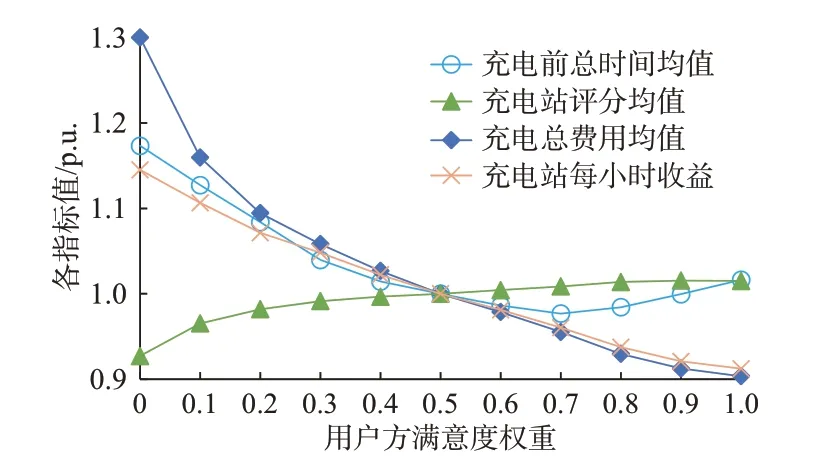
图5 各指标随用户方满意度权重变化趋势Fig.5 Trend of each indicator changing with weight of user-side satisfaction

图5 表明，随着用户方权重wuser的增大，充电总费用逐渐下降，且由于停车费用减少，下降速率略小于充电站每小时收益，同时，所推荐充电站评分逐渐增加；wuser增大到0.7 后，继续增大wuser时的充电前总时间标幺值反而略有上升，原因是用户更加期望前往高分、低价充电站充电，导致行驶时间有所增加。降低用户方权重wuser，可增加充电站每小时收益，但也会增加用户支出的充电费用。