车联网环境下电动汽车主动充电引导模型

袁晓冬，甘海庆，王明深，滕欣元，阮文骏，龙 寰

（1.国网江苏省电力有限公司电力科学研究院，江苏省 南京市 211103；2.国网江苏省电力有限公司，江苏省 南京市 210024；3.东南大学电气工程学院，江苏省 南京市 210096）

0 引言

近年来，电动汽车的销售规模不断扩大，受到中国政府部门、能源企业以及汽车制造商的关注［1-2］。相比于传统燃油汽车，电动汽车具有绿色经济的优势［3］。同时，由于具有负荷和电源双重性质，电动汽车也可参与电网辅助服务以支撑电网稳定控制［4］。电动汽车用户行为习惯、各类型电动汽车保有量的变化、电动汽车类型［5］以及充电站选址等因素会导致电动汽车堆积在某一个或某些特定的充电站，特别是在充电行为高峰期［6-7］。因此，国内外对电动汽车充电路径规划、选站策略这一课题展开了深入研究。

在电动汽车路径规划方面，由于电动汽车出行路径、驾驶需求等会影响交通侧道路的顺畅程度，交通信息会影响电动汽车充电路径选择［8］。同时，随着城市化进程和交通路网的大力发展，全局搜索算法在计算速度上无法适应实际场景的需求［9］。在减小无用搜索方面，文献［10］指出了A*算法的平均搜索节点比静态Dijkstra 算法减少50%以上。在城市路网场景下，由于路网节点较多，交通状态变化迅速，基于动态路网的路径规划问题成为研究热点［11-12］。文献［13］提出了一种以平均道路速度为权重的定向交通网络模型，旨在通过交通网调度最小化给定车辆数的充电时间并提高充电效率。但该文献将城市路网不同部分的通行速度简化为不随时间变化的平均值，未考虑实际路网存在的因转弯、拥堵等情况造成的动态时间消耗。文献［14］提出了一种车辆通过车联网通信向智能交通系统传递基本信息，进而利用智能交通系统寻找最优充电站的调度方法。在实验部分，该文献将所有车辆在道路上的行驶速度均设为相同值进行仿真，同样未考虑在实际路网中行驶时存在的不可控因素造成的时间损耗。文献［15］提出了一种结合了灰狼优化算法和旗鱼优化算法的灰色旗鱼优化算法，通过智能交通系统的调度提高交通效率，进而优化充电调度。在案例仿真部分，该文献设定电动汽车的速度为恒定值，并以此推算出不同车辆密度下在一定空间范围内电动汽车前往最近充电站的平均距离，进而判断所提出的算法是否有效缩短了电动汽车前往充电站的通行时间。由此可见，现有相关文献虽使用了动态路径规划方法，但在路网建模方面较为粗糙，通行时长常定义为与道路长度相关的线性函数。在实际城市路网中，由于存在大量红绿灯、交通堵塞等情况，简单地将路网建模为线性模型将与实际情况产生较大的偏差，亟须在路径规划阶段精细化路网的建模以符合实际城市路网场景。

在电动汽车充电站等待时间预测，特别是短期预测方面现有研究较少。在车联网背景下，文献［16］权衡时间感知公平性和电动汽车整体等待时间，提出了一个双目标充放电调度模型。文献［17］提出了一种基于时空图卷积网络的电动汽车充电站运行状态预测模型，通过预测电动汽车充电站使用情况来预测电动汽车充电等待时间。文献［18］提出了一种公共充电站占用率预测模型，对电动汽车用户等待时间进行预测。但是以上研究中均采用统计方式得到数据指标，忽视了电动汽车到站的随机性和周边交通路网的实时变化性。文献［19］介绍了一种考虑“路-车-源-荷”多重不确定性因素的交通网与配电网概率联合流分析方法，在考虑拥堵效应下电动汽车的等待时间时，将等待时间与电动汽车在该充电站的平均排队时间相关联而建立关系式。文献［20］表明，以单一车辆为例，用户的充电时间受当日或近期的出行规划影响较大。文献［21］以电动出租车为研究对象，对充电站排队系统内的车辆到达间隔时间和充电时长进行了统计分析，建立了M/G/k 排队论模型，提高了充电站排队系统的服务能力。但在车联网背景下，利用网联的充电站实时数据可以更有效地处理用户的短时倾向，预测充电等待时长的时变分布，为电动汽车主动充电引导提供依据。

针对上述问题，本文提出了一种车联网环境下的电动汽车主动充电引导方案。基于改进A*路径规划算法，求解实时路网状态下电动汽车充电路径时间花费；基于深度置信网络（deep belief network，DBN）模型，预测充电站的电动汽车短时到达率，采用排队论M/G/k 模型，完成电动汽车充电等待时间短时预测，实现电动汽车主动充电引导。

1 电动汽车主动充电引导架构

本文提出的车联网环境下的电动汽车主动充电引导方法从用户角度出发，目标是最小化用户的时间成本，如式（1）所示。

式中:Ttotal为电动汽车用户充电综合时长；Troad为电动汽车路径行驶时长；Twait为电动汽车充电站排队等待时间。

电动汽车主动充电引导方法架构如图1 所示。当用户发出充电需求指令，标定出发点O和备选充电站集合D，对所有备选充电站di∈D，根据改进A*算法进行初次路径规划，获取车辆到达备选充电站di的预计路径行驶总时长troad，i。以时间、物理环境量、di周边实时交通状态量、di车辆历史到达量为输入，基于DBN 预测电动汽车到达量λi，选取历史充电服务时长分布，确定di的M/G/k 排队论模型，以当前充电站状态和troad，i为初始化状态，基于蒙特卡洛（Monte-Carlo，MC）采样预测troad，i时间后备选充电站di的充电等待时间twait，i。计算总时间成本ttotal，i，拥有最小ttotal，i的充电站为最优备选充电站dbest，其到达路径标记为最优路径pbest。电动汽车沿推荐最优路径pbest行驶，在从节点Vi移动到下一个节点Vi+1前完成如下工作:

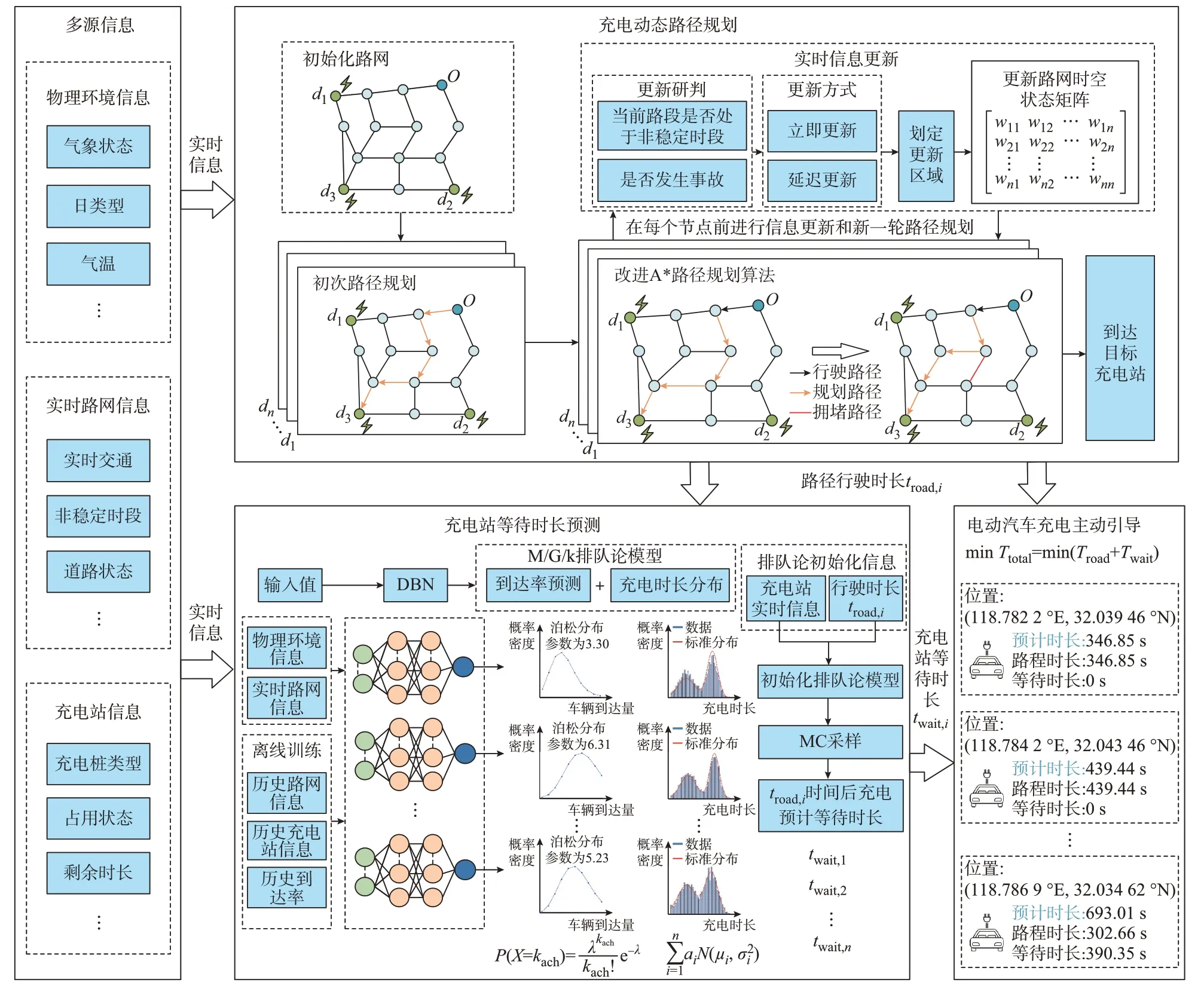
图1 车联网环境下电动汽车主动充电引导方法架构Fig.1 Architecture of active charging guidance method for electric vehicles based on Internet of vehicles

1）以当前节点Vi和目标充电站di两点连线外扩x距离所组成的矩形为标准，划定路网状态更新区域A，根据区域内的道路是否处于非稳定时段、是否发生事故，决定路网信息的更新方式，更新路网时空状态矩阵W；

2）使用改进A*算法，求解下一个节点Vi+1至终点di的预计通行时间troad，i和路径pi；

3）基于DBN 预测电动汽车到达量λi，选取历史充电服务时长分布，确定di的M/G/k 排队论模型，以当前充电站状态和troad，i为初始化状态，基于MC采样预测troad，i时间后备选充电站di的充电等待时间twait，i；

4）计算总时间成本ttotal，i，选择最小ttotal，i的充电站为最优备选充电站dbest，其到达路径标记为最优路径pbest。

车辆按照最优路径pbest向最优备选充电站dbest前进，直至到达。

2 电动汽车充电动态路径规划

2.1 时变路网建模

本文所研究的城市路网区域包含M条道路、N个道路节点，可用式（2）所示的图论G=（V，E，W）方式描述。

式中:节点V表示N个道路节点，即路口；边E表示交通图G中的M条城市道路。

城市交通的状态通常由交通流量、速度和密集度衡量［22］，但在本文的设定中，电动汽车主动充电引导方案以时间为导向，故将道路通行时长作为路网时空状态矩阵W的元素，如式（3）所示。

式中:Eij为0-1 变量，其值取1 表示节点Vi与节点Vj存在直连道路，否则其值取0；tij、lij、vij分别为道路（Vi，Vj）的通行时长、长度和平均车速。

由于城市路网较为密集，矩阵W的更新将占用大量的时间和计算资源，故有必要减少矩阵W的更新范围和频率。在更新范围方面，将更新区域A限定为以电动汽车当前节点Vi与目标充电站di两点为对角线所组成的矩形长宽分别外扩x距离的矩形，仅对更新区域A内的路网情况进行更新；在更新频率方面，通过引入道路车速不稳定时间段和交通事故状态量实现。

2.1.1 道路车速不稳定时间段

通过对已有城市交通流量速度的分析，由于早晚高峰的存在，同一条道路的通行速度在一天内呈现周期性，传统将道路通行时长简单定义为一个关于道路长度的线性函数的方式在城市场景下并不适用。因此，为了降低更新频率，引入道路车速不稳定时间段的概念。

基于市内各道路平均行驶速度数据集，以10 min 为间隔，根据式（4）计算某道路日平均行驶速度的变化，根据式（5）计算平均速度变化率。

式中:T为天数；vt，n为第n天时段t某道路的通行速度；为该道路时段t的平均通行速度；vt，tr为平均通行速度变化率，在本文中，将|vt，tr|＞0.15 的时段设定为某道路的车速不稳定时间段，其余时间段为车速稳定时段。因此，对于G内的不同道路（Vi，Vj），定义有不稳定时段集合={T1，T2，…，Tn}。

在更新矩阵W时，对于更新区域A内的某道路（Vi，Vj），当时段t处于不稳定时段，矩阵W以1 min的频率更新；当时段t处于稳定时段，矩阵W以10 min的频率更新。

2.1.2 交通事故状态量

对于图G中的每一条道路（Vi，Vj）设置交通事故状态标记位，默认为0，当发生事故时标记1，事故处理完毕标记为2，当标记为2 后5 min 变换为0。在更新矩阵W时，对于更新区域A内的某道路（Vi，Vj），当为1 或2 时，按1 min 的频率更新与道路（Vi，Vj）的首节点Vi和尾节点Vj直接相连的路网，以保证获取路网最新信息。

2.2 基于改进A*算法的动态路径规划

相比于静态路径规划Dijkstra 算法，A*算法依靠在决策函数F（·）中加入预估项H（·）以规避搜索明显对最优路径结果不产生影响的道路，提高搜索效率［23］。具体地，当电动汽车所在道路的后驱节点，即下一节点为Vi时，A*算法的决策函数如式（6）所示。

式中:F（i）为决策函数，其值越小，搜索优先级越高；G（i）为已知项，在传统A*算法中即为起点到后驱节点Vi消耗的总时间代价，在城市道路中，由于红绿灯广泛存在，故本文引入红绿灯机制，对已知项G（i）进行改进；H（i）为预估项，表示后驱节点Vi到终点的预计时间代价。

图2 展示了本文对A*算法的2 种改进。针对已知项G（i），在城市道路中，由于红绿灯广泛存在，故本文引入红绿灯机制，对已知项G（i）进行改进，将红绿灯等待时间设置为节点权值，加入到已有项G（i）中。在城市路途，特别是短程旅途中，红绿灯等待时间将成为路径总耗时的重要组成部分，不可忽略不计。为此，在路径规划的初始化阶段，为图G内的每一条道路（Vi，Vj）的后驱路口节点Vi初始化红绿灯等待时间字典。

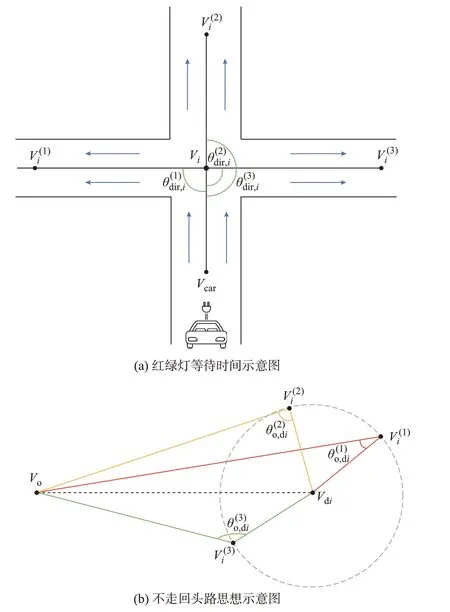
图2 A*算法的改进Fig.2 Improvement of A* algorithm

如图2（a）所示，在通过后驱节点Vi向终点探索路径时，Vi有直连节点Vdir，i={}。根据式（7），将Vi、∈Vdir，i（u=1，2，3）、车所处节点Vcar由经纬度坐标系转换为笛卡尔坐标系。

式中:Vi，xyz为节点Vi的笛卡尔坐标；Vi，x、Vi，y、Vi，z为节点Vi的笛卡尔坐标系参数；R为地球半径；Vi，lat和Vi，lon分别为节点Vi的纬度和经度参数。

式中:Vcar，xyz、分别为节点Vcar、的笛卡尔坐标。

将红绿灯等待时间计入此条探索路径的已有项Gnew（）中，参与A*算法后续更新，如式（11）所示。

式中:WEi，u为节点Vi到节点V(u)i所耗费的通行时长；tLight为根据夹角θ(u)dir，i从红绿灯等待时间字典t(Vi，Vj)Light中选取的等待时长。

针对预估项H（i），传统A*算法采用当前点到目标点的欧氏几何距离作为预估项，但在实际生活中，车主大多会倾向于选择调头较少的路径，即不走回头路。因此，本文在欧氏距离的基础上加入回头路惩罚项。

如图2（b）所示，在距离终点Vdi有相同欧氏距离的3 个点中，车主更倾向于选择或以避免调头行为。因此，本文将节点Vi的预估项H（i）定义为式（12）。

式中:si为节点Vi到终点Vdi的欧氏距离；vavg为电动汽车平均行驶速度；为起点Vo、节点、终点Vdi所构成的夹角，可由式（7）—式（10）计算得出；ω为惩罚系数。

基于改进A*算法的动态路径规划算法流程如图3 所示。

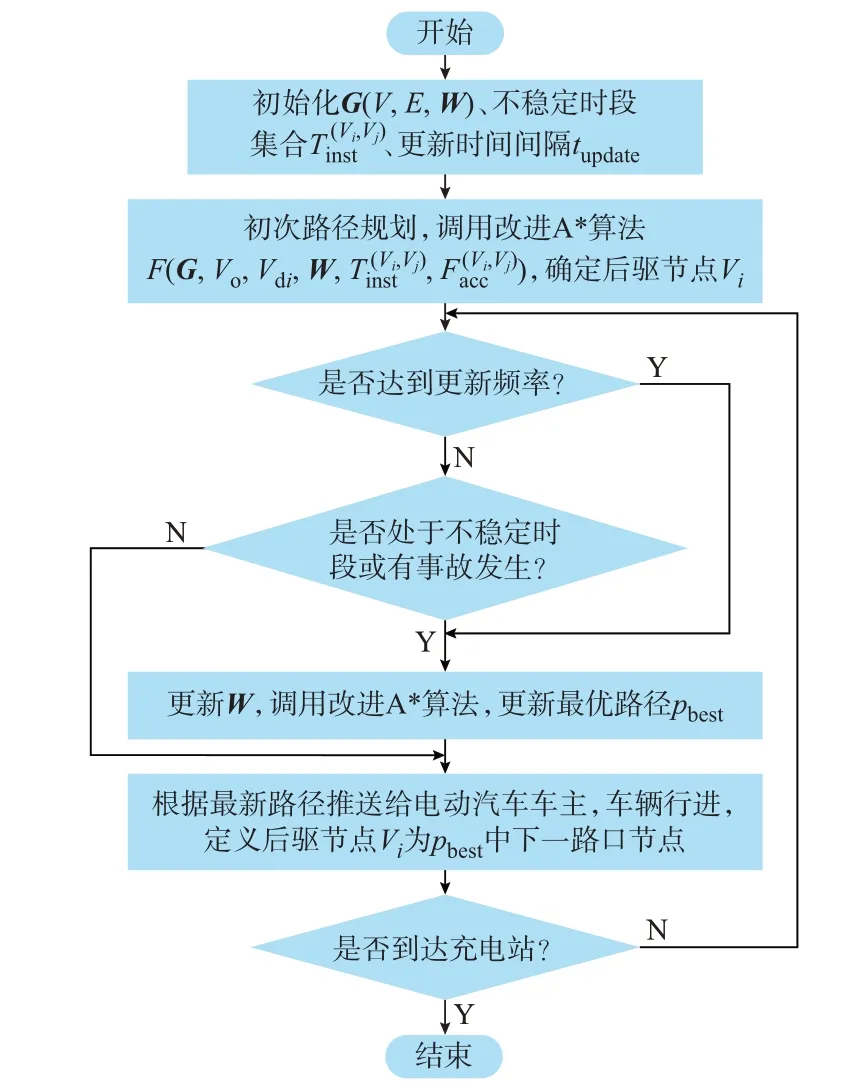
图3 基于改进A*算法的动态路径规划算法流程Fig.3 Flow chart of dynamic path planning algorithm based on improved A* algorithm

3 充电站等待时间预测

电动汽车充电方式分为快充和慢充，慢充大多在午夜进行，充电时长为7～10 h，对充电引导的需求不大［24］。因此，本文仅考虑城市内电动汽车选用快充桩进行快充的充电引导场景。电动汽车在充电站的充电行为满足排队模型，在此排队系统中，服务台数目为站内快充桩数目k，队列容量大小为∞，服务规程为单一队列先到先服务。因此，需要确定电动汽车到达和服务时长的数学特征以确定排队模型的具体类型。本文通过历史数据分析充电站到达车辆数据分布和电动汽车充电时长分布，确定排队模型为M/G/k。

3.1 充电站到达车辆数据分布

本文对某城市中心区域5 个电动汽车充电站06:00—21:00 的历史数据进行解析，以20 min 为单位统计到达车辆数，每天每站共计45 段数据。利用Kolmogorov-Smirnov 检验（K-S 检验）确定数据是否服从如式（14）所示的泊松分布。

式中:X为随机变量；λ为单位时间内随机事件的平均发生次数，即车辆到达率。

检验结果表明p-value 均大于0.05，不拒绝原假设，即可以认为充电站到达车辆数服从泊松分布。到达车辆数泊松分布部分K-S 检验结果见表1。

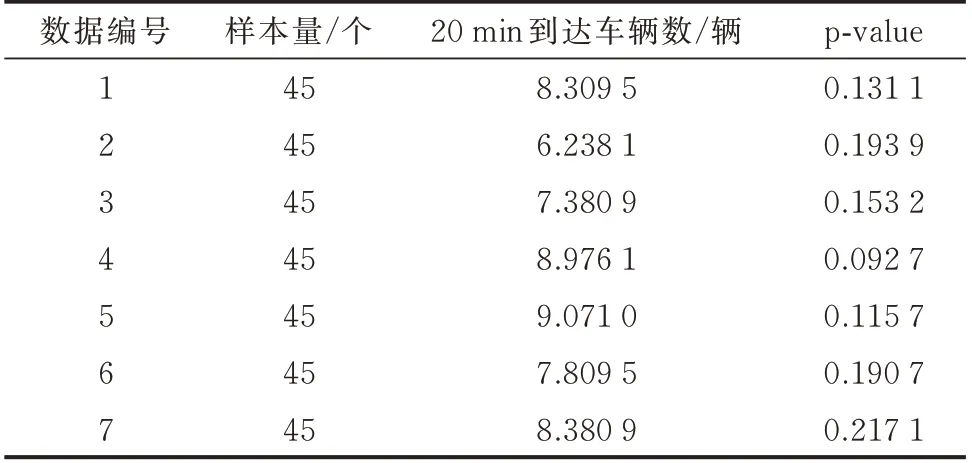
表1 到达车辆数泊松分布部分K-S 检验结果Table 1 Partial K-S test results for Poisson distribution of numbers of arriving vehicles

3.2 基于DBN 的电动汽车到达量预测

根据历史数据可以发现，在相同日类型下，电动汽车到达量的变化趋势相似［25］，考虑到电动汽车用户充电行为的随机性和实时性，鉴于神经网络模型在非线性建模、噪声容错、泛化能力等方面的突出优势，本文采用基于DBN 的单位时间电动汽车到达量短期预测模型。

本文选取的模型输入特征为历史车辆到达情况、时间、气象情况、环境温度、日类型、交通状况等6 类，数据需经矢量化处理和归一化处理。输入层数据包括预测时段前3 个时段、前3 日同时段、前3 个同一类型日（工作日/节假日）同时段的所有特征。输出为t时段的电动汽车到达量预测值λ。

DBN 模型的输入层和输出层之间由r个受限玻尔兹曼机（restricted Boltzmann machine，RBM）和1 个全连接层堆叠而成，分为无监督预训练和有监督微调2 个阶段［26］，如图4 所示。

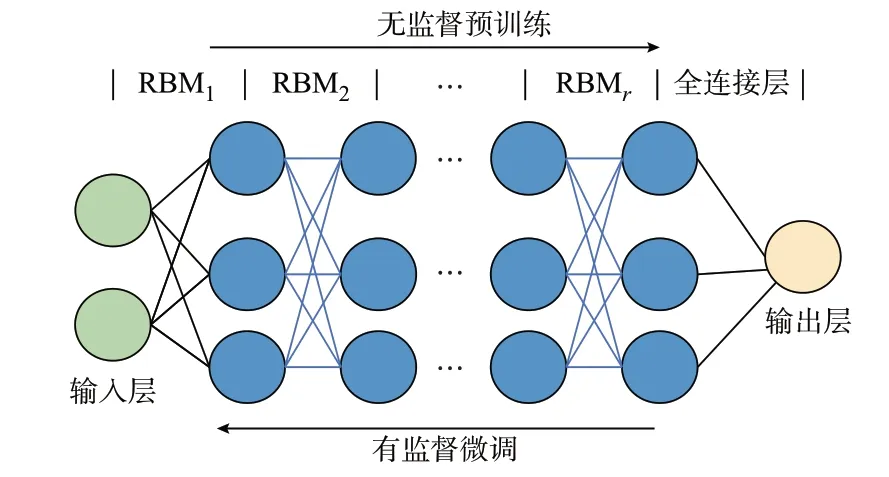
图4 DBN 结构示意图Fig.4 Schematic diagram of DBN structure

在无监督预训练阶段，RBM 采用最大似然估计的方式训练，期望获得最小能量，其参数优化目标函数如下:

式中:Ts为样本数；J（·）为RBM 的能量函数；参数θ=(a，b，Wpar)，其中，a为可视层参数，b为隐含层参数，Wpar为可视层和隐含层之间的权重矩阵；h为隐含层表示在特定样本ts下的可视层的状态。利用对比散度算法求解最优参数。

在有监督微调阶段，基于交叉熵构建损失函数，并构建RBM 优化目标函数，如式（16）所示。

本文选用平均绝对误差（mean absolute error，MAE）和均方根误差（root mean square error，RMSE）作为评价指标。

3.3 电动汽车充电时长分布

在此排队模型中，服务时长即为电动汽车在充电站的充电时长。本文对上文所述的5 个充电站相同观测时段内的电动汽车充电时长数据进行分析。

由图5 可知，以充电站为划分依据，所选站的电动汽车充电时长显然不服从于已有文献所指出的负指数分布、正态分布或伽马分布［27-29］，而近似服从于式（17）所述的混合高斯分布。

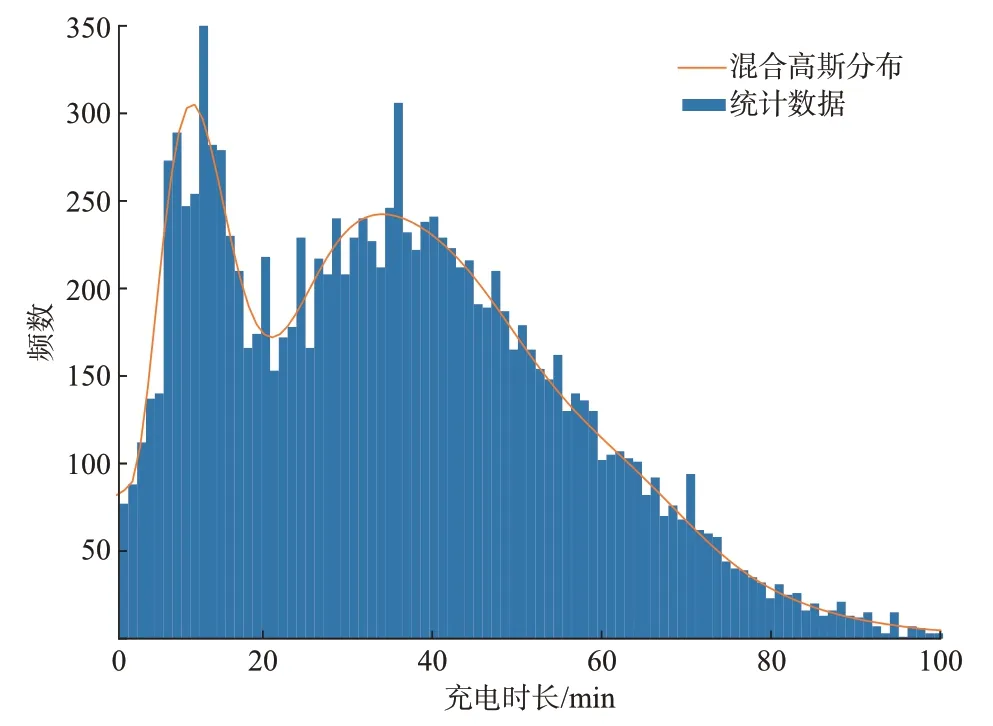
图5 充电站1 中充电时长统计分布Fig.5 Statistical distribution of charging duration at charging station 1

式中:Tch为充电时长分布；NG为高斯分布组件数；ai为混合高斯分布的权重；N（μi，）为标准高斯分布，其中，μi为均值，为方差。基于同一充电站同一时段的电动汽车充电时长历史数据，通过计算混合高斯模型的贝叶斯信息准则（Bayesian information criterion，BIC）并与其他模型进行比较，以此来评估模型的拟合优度，较低的BIC 值通常表示更好的模型。因此，选择BIC 值最小的模型，确定高斯分布的数量，对于每一个高斯分布组件，获取其权重ai、均值μi和方差σ2i，得到充电站i电动汽车充电时长分布。

3.4 电动汽车充电站等待时间预测

基于以上分析，本文所研究的电动汽车在充电站充电符合M/G/k 排队模型。由于M/G/k 排队论问题暂无解析解，故本文采用MC 采样的方法获取电动汽车充电等待时间的短期预测。

对于目标充电站di，首先构建单队列排队模型，接着以车联网获取的充电桩实时信息初始化模型，通过DBN 获取当前时段的车辆到达率λi，t，将其代入式（14）获得当前时段t的电动汽车到达量分布Pi，t，结合电动汽车充电时长分布Tch，i，通过MC 采样获取troad，i后（即车辆到达后）的电动汽车充电站平均等待时长，以此作为twait，i。具体步骤如下:

1）建立了k个队列用于仿真充电站中的k个充电桩，根据桩当前的状态（剩余充电时间）初始化k个队列，如果桩未被占用，则存入0；

2）根据3.2 节和3.3 节所得的分布，采样得出未来时间troad，i内车辆到达的时间点和充电时长；

3）以先来先服务的模式模拟未来时间troad，i内车辆到达和排队的情况（即优先选择队伍等待时间较短的队伍进行等待），记录下时间troad，i后车辆的等待时间；

4）循环足够多次取平均值（即电动汽车充电站平均等待时长）作为twait，i。

4 实例分析

本文选取中国南京市中心区域城市路段进行实例分析，地图数据来源于开源平台OpenStreetMap，并通过开源地理信息系统QGIS 进行处理，其中，共有149 个路口节点、233 条道路、5 个充电站节点，见附录A 图A1。本文的计算环境为单个16 核CPU（3.80 GHz AMD Ryzen7 5700G with Radeon Graphics），集成开发环境为PyCharm。

4.1 基于改进A*算法的动态路径规划

为了验证动态路网状态信息对路径规划结果的影响，将本文设计的基于改进A*算法的动态路径规划算法与静态Dijkstra 算法进行比较，结果如图6所示。

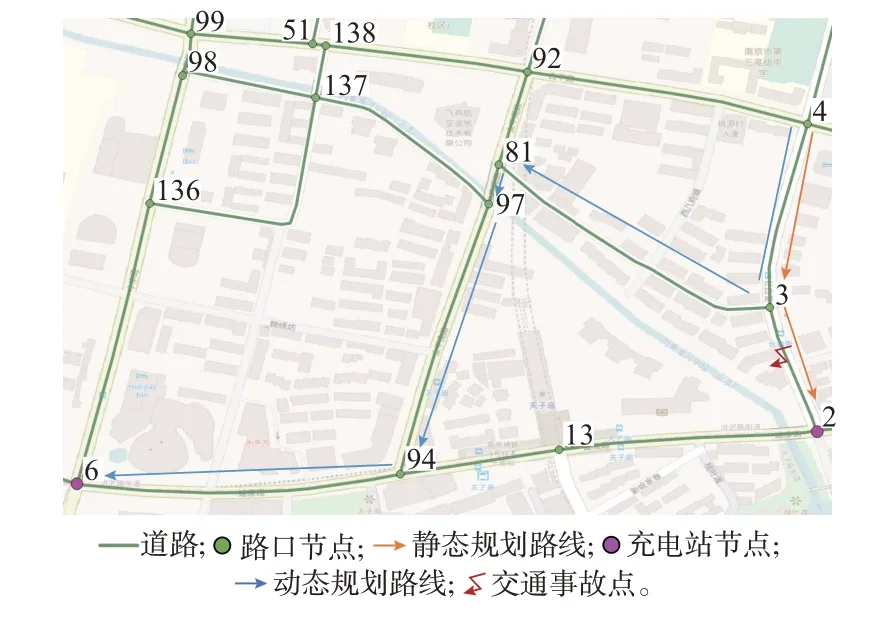
图6 基于改进A*算法的动态路径规划算法与静态Dijkstra 算法结果比较Fig.6 Result comparison between dynamic path planning algorithm based on improved A* algorithm and static Dijkstra algorithm

设定案例的电动汽车起始点为节点4，范围内有2 个充电站，分别在节点2 和节点6。初始动态算法与静态算法的规划路径均为［4，3，2］，在40 s 后，网联数据检测到节点3-节点2 路段发生事故，通行速度放缓，此时车辆正行驶在节点4-节点3 的路段上，动态算法开始更新路网时空状态矩阵W，并重新基于改进A*算法再次进行路径规划，耗时25 ms，规划出新路线［4，3，81，97，94，6］，虽然选择了路程较长的路径，但是成功绕过拥堵路段。动态规划路线路径行驶时间为429.2 s，静态规划算法路径行驶时间为496.8 s。结果表明，本文提出的基于改进A*算法的动态路径规划算法可以实现车辆实时引导，规避交通拥堵路段，实现最小化通行时间。

为了验证改进A*算法的高效性，在区域内使用Dijkstra 算法和改进A*算法，并在求解过程中进一步使用小根堆数据结构进行优化，分别随机进行5 000 次路径规划，计算耗时结果如表2 所示。结果表明，改进A*算法由于增加了方向性限制，减少了无效的空间搜索，较Dijkstra 全局静态路径规划算法计算效率提高了73.67%，采用小根堆结构的改进A*算法将寻找F（·）最小值的时间复杂度从O（n）下降为O（logn），故其计算效率进一步提高。由上述2 个实验可以表明，基于改进A*算法的动态路径规划可以满足城市导航所需的高效性和及时性需求。

表2 区域内随机5 000 次路径规划不同算法计算时间Table 2 Calculation time of different algorithms for 5 000 random path planning within region

4.2 基于DBN 的电动汽车到达量预测

采用充电站1 于2021 年5 月至2022 年2 月的实际运行数据，以及期间的气象、温度、类型日、交通数据，经矢量化和归一化处理后，作为输入数据。分别用本文所述DBN 模型、随机森林（random tree，RF）模型、支持向量机（support vector machine，SVM）模型、决策树（decision tree，DT）模型获取预测结果，如表3 所示。结果表明，DBN 相比于其他3 种算法，其MAE 和RMSE 均较低，且误差可以接受，该算法可深入挖掘车辆到达率与输入特征间的关系，精度相对较高，可以用于预测电动汽车充电站的到达率。

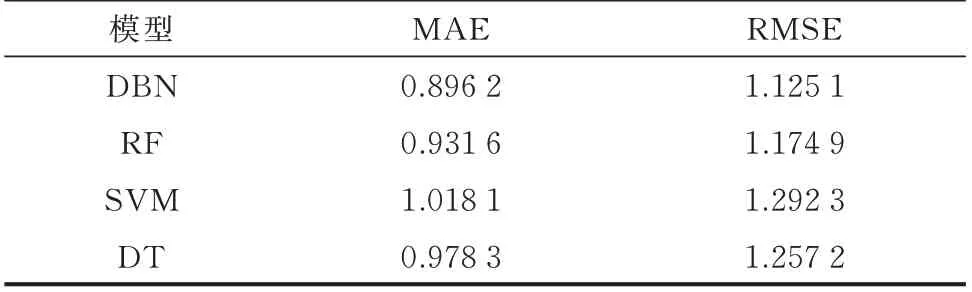
表3 不同预测算法性能比较Table 3 Performance comparison of different prediction algorithms

4.3 电动汽车主动充电引导算例

为了验证本文所提主动充电引导模型的有效性，本实验取一典型日的交通状况、气象状况、温度状况，在区域内随机生成900 辆有充电需求的电动汽车，分别按本文所述主动充电引导方案和静态路径充电引导方案（以下简称“静态引导”）进行实验，其中，静态引导采用Dijkstra 最短路径静态路径规划算法，选取路程最近的充电站进行充电引导。统计所有电动汽车路径行驶总时长∑troad、充电站排队等待时间总时长∑twait和电动汽车用户充电总综合时长∑ttotal。下降率按式（18）计算所得，实验结果如表4 所示。

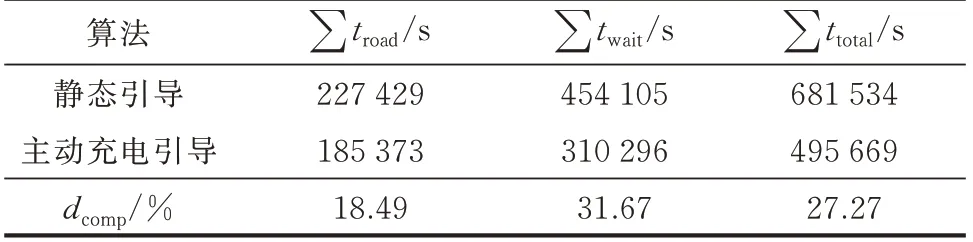
表4 主动充电引导算法与静态引导算法充电结果对比Table 4 Charging results of active charging guidance algorithm and static guidance algorithm

式中:dcomp为下降率；tsta为采用静态方法进行引导的时间；tpaper为采用本文方法进行引导的时间。

表4 结果表明，本文所提主动充电引导方案在减少路途时间以及减少充电站等待时间方面都效果显著。路径行驶时长下降18.49%，充电站排队等待时间下降31.67%，充电综合时长下降27.27%，验证了本文所提电动汽车主动充电引导方案在车联网及城市路网背景下的有效性。

在以上实验的基础上，计算区域内5 个充电站的等待车辆数量和充电站充电桩使用率。如图7（a）所示，在采用静态算法引导时，由于充电需求和规划因素，充电站1 和充电站3 聚集大量车辆，使得这2 个站的充电等待时间较长；采用本文主动充电引导方法后，电动汽车被主动引导至其余充电站，各充电站等待车辆数均处于低位。如图7（b）所示，主动充电引导方法的对应整点时刻充电桩占用率明显高于基于静态算法的引导充电方法，改善了基于静态算法的引导充电导致的充电站使用率不平衡问题，该区域15:00—16:00 时段充电站的平均利用率由69.50%提升至89.47%，论证了本文所提车联网环境下电动汽车主动充电引导方案可以提高充电桩的利用率。

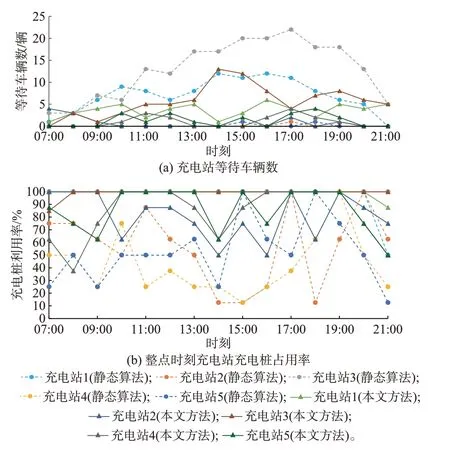
图7 5 个充电站的等待车辆数量和充电桩占用率实验结果Fig.7 Test results of number of waiting vehicles and utilization rate of charging piles at five charging stations

5 结语

本文利用车联网环境下电动汽车动态信息，提出了一种基于改进A*路径规划与排队论的电动汽车主动充电引导模型。融入红绿灯等待时间和不走回头路思想，改进城市路径规划A*算法中的已有项G（·）和估算项H（·），利用实际路网状态信息更新路网时空状态矩阵，求解电动汽车充电路程花费时间，确保电动汽车在到达下一个节点前获取最优规划行驶路径。确定充电站到达车辆数以及电动汽车充电时长分布，基于DBN 预测电动汽车到达量，确定更新策略，采用排队论M/G/k 模型，利用MC 采样预测短时间内电动汽车充电等待时间。根据电动汽车充电路程花费时间和电动汽车充电等待时间，提出电动汽车主动充电引导方法。本文创新和贡献如下:

1）改进A*算法并应用于城市场景下的动态路径规划，在车联网环境下，确保电动汽车行驶路径最优，并验证了其准确性。

2）基于DBN 算法预测充电站车辆到达量，充电站等待时长短时预测采用M/G/k 模型具有普适性。

3）提出了用户视角下考虑路径行驶时间和充电站等待时长的主动充电引导方案，并验证了其高效性。

在本文研究中，对于价格因素对电动汽车车主选站的影响考虑得并不充分，且只为用户给出了一个最优充电站和其匹配的最优充电路径，未给出后备方案。未来，可将深度强化学习算法引入路径规划中，使其更为高效；通过增加价格因素，以系统最优和用户均衡为目标对电动汽车用户的充电需求进行分配，进一步减少用户的充电成本，提高充电站的利用率。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。