计及多重不确定性的规模化电动汽车接入配电网调度方法

李金鹏，冯 华，陈晓刚，章寒冰，占震滨，许银亮

（1.清华大学深圳国际研究生院，广东省 深圳市 518000；2.国网浙江省电力有限公司丽水供电公司，浙江省 丽水市 323000；3.国网浙江省电力有限公司，浙江省 杭州市 310027；4.国网浙江省电力有限公司电力科学研究院，浙江省 杭州市 310014）

0 引言

截至2023 年6 月底，中国电动汽车（EV）保有量已经超过1 200 万辆，大规模接入电网的EV 若不进行合理调度，将对电网安全运营带来严峻挑战［1］。同时，EV 作为一种具有时空和容量高度灵活性的负荷，具有很大的调节潜力，可以作为灵活性资源为配电网提供辅助服务并带来安全效益，增强电力系统管控不确定性风险的能力。

单辆EV 调节能力有限，无法参与电力市场，EV 聚合商作为EV 与配电网的中间体，能够管理EV 充放电和电力市场交易，与配电网进行互动［2］。通过建立EV 聚合模型，便于从整体角度分析EV 集群的可调节潜力，减少模型中的变量个数，降低模型复杂度与EV 数量的关联［3］。EV 接入和离开充电站的时间、充电需求、渗透率日益增加的光伏/风电等可再生能源、电网中的非灵活性负荷等均存在着不确定性，如何处理不确定性是EV 并网充放电调度研究中的关键性问题［4］。

现有处理不确定性的经典方法包括随机优化（SO）［5-6］、鲁棒优化（RO）［7-8］、机会约束［9-10］等。其中，SO 一般以目标函数的数学期望为目标，如文献［11］考虑了EV 到达/离开时间、非灵活性负荷、市场价格的随机性，最大化配电网和EV 聚合商利益的期望值。然而，SO 往往需要场景驱动，复杂度与场景的数量高度相关，场景过少可能导致对随机性的刻画不准确，场景过多则带来很大的计算负担。与SO 不同，RO 关注可能出现的最坏情况，如文献［12］考虑随机的可再生能源出力和负荷，通过强对偶理论和列与约束生成算法来转化和求解两阶段RO 问题。与SO 问题相比，RO 复杂度与场景的个数关联较低，但由于最坏的情况在实际中可能以很低的概率出现，这种方法可能过于保守。此外，由于SO 和RO 均未将风险系数考虑在建模中，无法直观地管理系统风险。

为解决SO 和RO 方法存在的问题并平衡经济成本与系统安全，分布式鲁棒机会约束（distributionally robust chance constraint，DRCC）模型受到越来越多的关注［13］。文献［14］通过建立DRCC 模型处理了非灵活性负荷、可再生能源出力、市场价格等不确定性因素。文献［15］采用机会约束限制电压、功率等范围以确保配电网在一定概率下安全运行。文献［16］采用DRCC 模型对EV 的可调空间进行建模。然而，上述研究中的多个机会约束是独立的，忽视了机会约束之间可能存在的关联，同时在单一机会约束的风险参数选择上具有一定主观性，如文献［15-16］均对每条约束取相同的风险等级。为此，有必要联合考虑机会约束，将问题建模为分布式鲁棒联合机会约束（distributionally robust joint chance constraint，DRJCC）模型。然而，DRJCC 模型是隐式的，难以求解，经典的Bonferroni 近似（Bonferroni approximation，BA）方法直接将联合约束转化为独立约束，并根据Bonferroni 不等式预先分配独立约束的风险等级，这可能导致模型过于保守。为降低模型保守性，文献［17］提出最优Bonferroni 近似（optimized Bonferroni approximation，OBA）方法用于近似机会约束问题，这种方法在满足Bonferroni不等式的前提下将独立约束的风险等级也视为变量进行优化，可以降低模型的保守性。进一步地，文献［18］将OBA 方法求解DRJCC 问题应用到考虑不确定性的潮流问题中，提出了基于多项式展开近似、连续凸近似等方法，并对比了不同近似方法的表现。尽管对采用OBA 方法求解的DRJCC 模型已有了初步的研究，但其应用在大规模EV 接入配电网的调度研究中尚且罕见。为此，本文在大规模EV 接入配电网的调度问题中建立了DRJCC 模型，联合考虑了节点电压、线路功率、备用需求，并采用OBA 的方法求解。与相关研究相比，本文的主要贡献如下:

1）为高效处理多重随机性下EV 接入配电网的调度问题，建立了DRJCC 模型，算例表明所提模型缓解了SO 模型求解时间长［19］、RO 的模型过于保守等问题［20］。

2）为处理难以求解的联合机会约束模型，提出一种OBA 方法，将风险等级也视为决策变量，将问题转化成混合整数二次规划模型，降低了模型的保守性，与预先确定风险等级的方法［14-16］相比，在满足可靠度要求的前提下降低约6.5%的成本。

3）所提模型将节点电压、支路功率、备用需求等综合考虑作为联合机会约束建模，能够通过设定系统整体风险等级参数以直观管理系统风险，并便于平衡系统运营成本和可靠度。

1 EV 接入配电网的DRJCC 模型

本文考虑的多重不确定性包含除EV 充电负荷外的净负荷的不确定性和EV 负荷的不确定性两个维度，净负荷和充电负荷的不确定性分别影响配电网和充电站的备用需求。将不确定性分为净负荷和充电负荷两类考虑的原因主要有:净负荷与EV 负荷可能具有不同的分布特性，分开建模便于对概率分布进行拟合；配电网和EV 充电站属于不同主体，分开建模能够使风险等级的物理意义更为明确，例如，配电网侧电压/功率越限风险、配电网侧备用不足风险、充电站侧备用不足风险等。

1.1 目标函数

目标函数如式（1）所示，为最小化充电站与配电网的总成本，包括从上级电网购买电能和备用的成本、配电网所辖分布式发电机组的发电和备用成本、充电站的充电成本和向EV 用户支付的放电补贴成本。

1.2 EV 聚合能量可行域约束

2）EV 能量约束

式中:Ei，t为t时刻节点i处EV 的能量；分别为节点i处EV 的充、放电效率；Δt为时间间隔；底标“-”表示对应变量的下限。

3）能量可行域的上下限

4）充电桩聚合的功率与能量约束

关于聚合的具体过程详见附录A。

1.3 配电网潮流约束

1）节点注入的有功、无功功率

2）支路上的有功、无功功率

式中:Vi，t、θi，t分别为t时刻节点i处电压幅值、相角。

3）从上级电网购电的容量约束

4）削峰约束

式中:B为所有节点集合；Mp为调度前负荷的峰值；β为削峰百分比。电压、功率的幅值约束在1.5 节中写为联合机会约束的形式。

1.4 备用市场约束

1）从上级电网购买和从发电机组发出的备用约束

2）备用的供需平衡约束

1.5 联合机会约束

节点电压、支路功率、备用需求的联合机会约束如式（19）所示。

式中:Ut、Vt分别为t时刻净负荷和充电需求总偏差的随机变量；ΔVi，t、ΔPij，t、ΔQij，t分别为t时刻节点i电压、支路ij有功功率和无功功率的偏差。式（19）意味着在t时刻由净负荷和充电负荷不确定性引起的备用需求和电压、功率的波动需要被同时以不低于1-ϵt的概率联合满足，其中，ϵt为t时刻系统整体的风险等级。

2 DRJCC 模型求解

2.1 随机变量概率分布的拟合

由式（8）—式（11）可得如式（20）所示矩阵形式，其中下标0 表示与上级电网相连的参考节点，下标c表示除参考节点以外的节点，有N-1 个。

式中:Pc，t、Qc，t、θc，t、Vc，t分别为节点c的有功、无功功率注入、电压相角、电压幅值的向量；BE=其中，B1，c和B2，c分别为B1和B2去除第1 行和第1 列的子矩阵；B1，0和B2，0分别为由B1和B2第1 列的第2 至第N个元素构成的向量；V0、θ0分别为参考节点的电压幅值和相角。

由式（20）可知，净负荷带来的误差导致电压幅值和相角的变化可以表示为:

式中:ξPl，nett为净负荷的误差；Δ 表示对应变量的变化量。

由式（21）知，电压幅值的灵敏度可写为节点净负荷变化的线性函数，即ΔVc，t=LV(ξPtl，net)。线路的有功和无功潮流变化为:

式中:Lij为长度为N的行向量，其中第i个元素为1，第j个元素为-1，其他元素为0；LP(·)、LQ(·)分别为有功和无功功率的灵敏度线性函数［21］。

Ut为t时刻系统除充电需求以外的净负荷的偏差值，可由光伏、风电出力和净负荷的偏差值叠加得到，Vt为t时刻充电需求的偏差值，可以通过对所有充电站t时刻下充电需求的偏差值［22］求和得到，由于Ut和Vt是解耦的，无须建立Ut和Vt的联合概率分布模型。

优化模型的求解中，需要已知ΔVi，t、ΔPij，t、ΔQij，t、Ut、Vt等随机变量概率分布的离散值，由于上述变量是通过随机变量ξx变换得到的，且这些变换是线性、离散、一对一的，可以先通过对ξx的历史数据进行对应的变换，生成ΔVi，t、ΔPij，t、ΔQij，t、Ut、Vt的数据样本，再通过高斯混合模型（Gaussian mixed model，GMM）拟合上述随机变量，其通式可表示为［23］:

由于联合机会约束式（19）是隐式的，上述模型难以求解。因此，提出基于BA 和OBA 方法的两个模型以求解上述问题。

2.2 基于BA 方法的模型求解

BA 方法将联合机会约束式（19）转化为独立约束式（25）—式（31）以便求解。其中，独立约束的风险等级ϵi，t满足Bonferroni 不等式，即般地，令各个风险等级相等，如式（32）所示，其中，n为式（19）中机会约束的个数。

式（19）与式（25）—式（32）的等价关系证明见附录B。 式（25）— 式（31）可转化为式（33）—式（39）。

至此，联合机会约束被转化成独立的线性约束，模型变为可解的凸问题。基于BA 方法求解的DRJCC 模型（下文简称BA 模型）的紧凑形式为:

2.3 基于OBA 方法近似的模型求解

上述BA 模型虽然能够给出联合机会约束的线性转换形式，但由于预先确定风险系数ϵi，t，导致模型过于保守。与BA 模型预先确定风险系数不同，提出一种基于OBA 方法的模型，将风险系数也视为决策变量，以减少模型的保守性。引入二元变量满足式（41），K为控制精度的参数，式（42）为Bonferroni 不等式，对应BA 模型中的式（32）。

式（43）为电压机会约束的转化形式，对应式（33）。

类似地，式（44）和式（45）为有功和无功功率的机会约束转化形式，分别对应式（34）和式（35）。

式（46）为应对净负荷随机性的向上备用机会约束转化形式，对应式（28）。

与上述证明过程类似，式（47）对应式（29）、式（48）对应式（30）、式（49）对应式（31）。

至此，联合机会约束被转化为独立的混合整数线性约束，可用商业求解器求解。基于OBA 方法求解的DRJCC 模型（下文简称OBA 模型）的紧凑形式见式（50），式（50）所示是混合整数二次规划问题，可以通过常见的商业求解器求解。

式中:X表示与BA 模型相同的决策变量，另须注意OBA 模型中需要优化的变量还包括风险等级ϵi，t。

3 算例分析

本章首先在修改的IEEE 33 节点系统上验证了所提模型的有效性，进而在修改的IEEE 123 节点系统上验证了所提模型对更大系统和更多EV 接入的可扩展性。下述算例均是在带有i5-12500 处理器和8 GB 内存的个人电脑上进行的，算法采用MATLAB 的YALMIP 工具箱构建，采用商业求解器Gurobi 10.0 求解。模型参数见附录C。

3.1 IEEE 33 节点系统验证结果

本节研究的IEEE 33 节点配电系统辖有3 个分布式发电机组、1 座光伏发电站和1 座风力发电站，有2 089 辆EV 通过4 个充电站接入配电网。具体的连接方式与网络结构见附录D 图D1。随机变量Ut、Vt的分布和GMM 拟合结果如图1 所示，可见GMM能够精准地拟合随机变量的分布。

图1 随机变量的分布和GMM 拟合结果
Fig.1 Distribution and GMM fitting results of random variables

3.1.1 所提模型对经济性和可靠度的平衡

将所提模型与经典的SO［24］和RO［25］进行对比，以验证模型平衡成本与系统风险的能力。其中，SO模型采用的是场景驱动的SO 模型，最小化多个场景中的期望成本，RO 模型中随机变量的不确定集与所提模型采用的不确定集相同。表1 给出了不同模型的运营成本、可靠度、求解时间等信息，其中，风险等级通过20 次独立的蒙特卡洛模拟得到，每次蒙特卡洛模拟均生成1 000 个场景，可靠度Re定义为这些场景下联合机会约束式（19）被满足的概率，表1 中列出了20 次蒙特卡洛模拟可靠度的均值Re，avg、最小值Re，min、最大值Re，max。

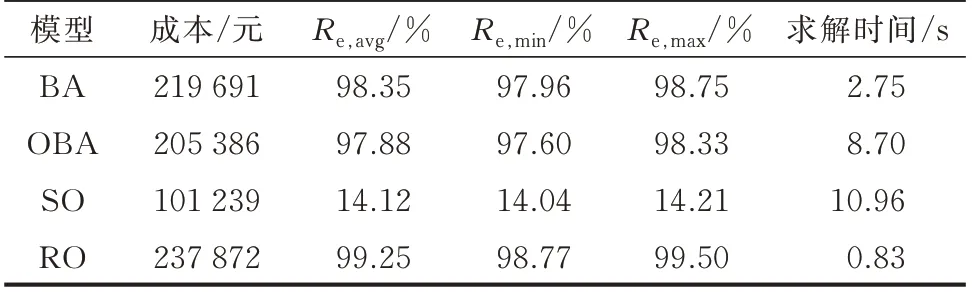
表1 不同模型的成本、可靠度和求解时间（ϵt=0.05）Table 1 Cost, reliability and solving time of different models with ϵt=0.05

由表1 结果可知，SO 模型的成本最低，但其可靠度无法满足95%的要求，且求解时间最长。RO模型的可靠度最高，但过于保守，可靠度显著高于要求值。相比RO 和SO，所提BA 模型和OBA 模型能够更好地平衡成本和可靠度。另外，所提模型能够通过调整参数ϵt控制整体风险，在实际应用时具有更大的灵活性。图2 展示了调整参数ϵt对模型的成本和可靠度的影响。

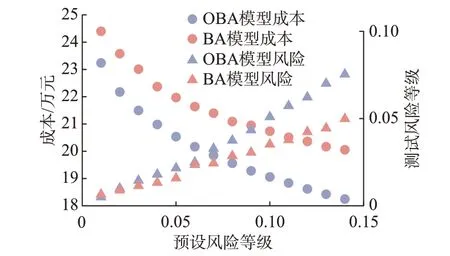
图2 不同预设风险等级ϵt 下模型的成本和可靠度Fig.2 Cost and reliability of models with different preset risk level ϵt

图2 结果表明，当预设风险等级较低时，与BA模型相比，OBA 模型能够进一步降低保守性，同时满足可靠度要求；当预设风险等级较高时，OBA 模型成本降低更加明显。这是由于OBA 模型将风险等级也视为决策变量进行优化，使得模型灵活度更高，能够以更为经济的方式满足可靠度的要求。

图3 展示了OBA 模型和BA 模型的备用结果，对比可知两个模型的总备用容量并没有显著差距，但备用的分配却有较大差异，这表明OBA 模型能够充分利用电价的时间差异性、随机变量的分布特性、多个约束之间的成本和可靠度的敏感性差异等作出更合理的决策。更为具体的讨论可参考附录E。

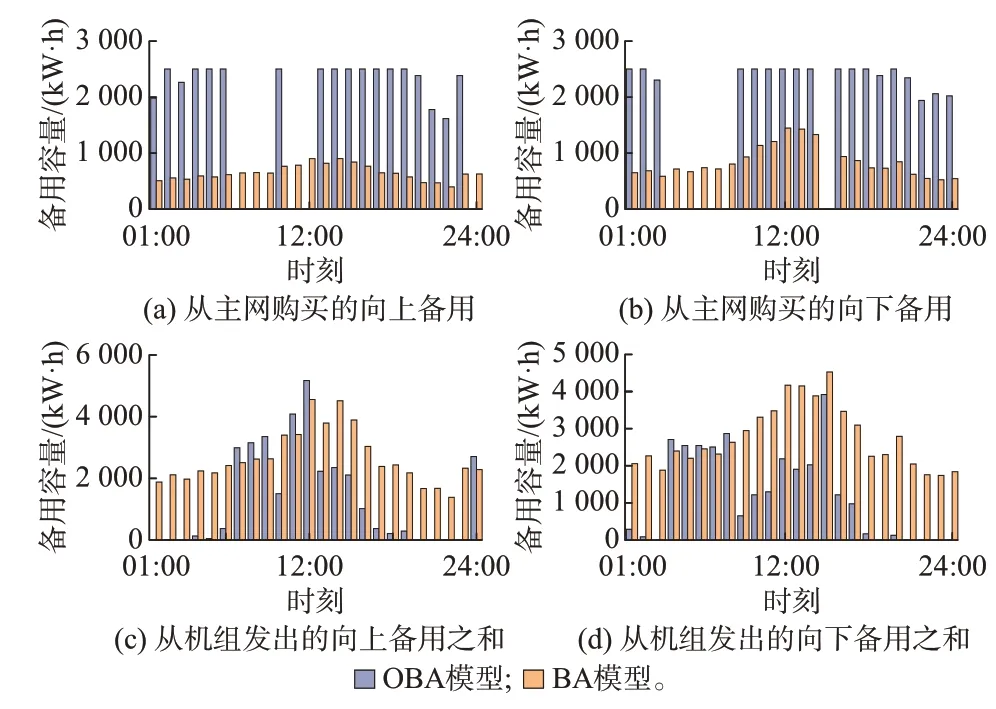
图3 OBA 模型和BA 模型求解得到的备用结果Fig.3 Reserve results solved by OBA and BA models

3.1.2 所提模型的充电曲线优化和负荷削减能力

图4 展示了连接在节点22 的充电站采用所提的BA 和OBA 模型与即来即充模型的能量可行域以及相应的充电曲线。从图中可以看出，即来即充曲线与能量可行域上界几乎重合，然而由于上界考虑了放电的可能性，比即来即充策略的范围更大。同时，BA 和OBA 模型的充电曲线十分相近，这是由于BA 和OBA 模型的区别在于备用分配和电压、功率流的约束上下限不同，因而会影响发电机组的策略，进而影响充电策略，但这一影响较小。与即来即充策略相比，OBA 与BA 模型的充电策略在中午和晚上的高峰电价时期充电曲线更为平缓，甚至出现放电的现象以获取额外的收益。在24:00 时刻处，可行域边界、3 个模型的充电曲线均收敛至同一位置，表明所提模型的聚合过程能够保证结果满足充电需求。

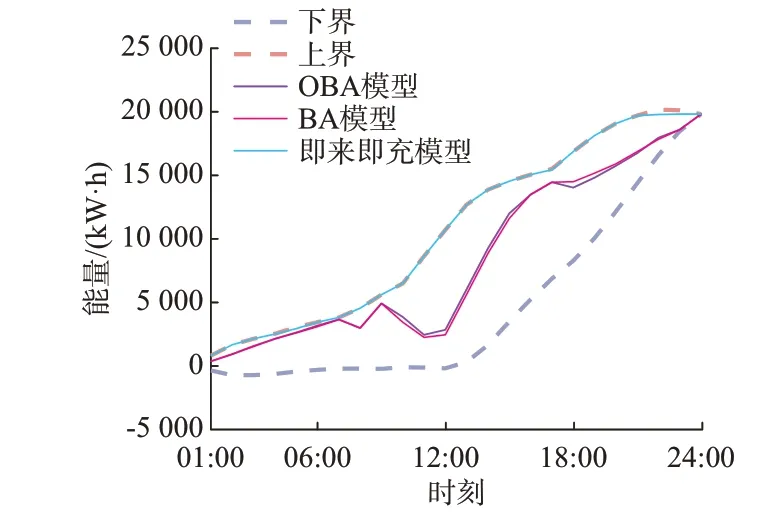
图4 OBA、BA 和即来即充模型的充电曲线Fig.4 Charging energy curves of OBA, BA and immediate charging models

对式（13）中的调峰参数β进行敏感性分析，结果见图5。可见所提模型能够利用EV 集群的灵活性满足不同的调峰需求，同时能够避免峰值电价时段的高峰负荷以降低成本。

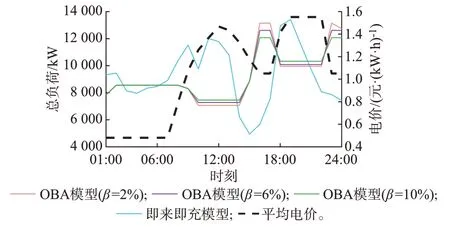
图5 不同削峰深度得到的总负荷曲线Fig.5 Total load curves obtained under different peak-shaving depth

3.2 IEEE 123 节点系统验证结果

本节研究的IEEE 123 节点配电系统辖有9 个分布式发电机组、3 座光伏发电站和3 座风力发电站，有4 404 辆EV 通过10 个充电站接入配电网。具体的连接方式与网络结构见附录D 图D2。

表2 列出了不同模型在IEEE 123 节点系统上的成本、可靠度和计算时间，其结果特征与表1 一致，表明尽管系统规模增长，所提模型仍能够较好地平衡成本和可靠度。对比表1 与表2 的模型求解时间可知，相较SO 模型，所提BA 和OBA 模型求解时间增长均较为平缓，表明所提模型对更大电力系统具有良好可扩展性。

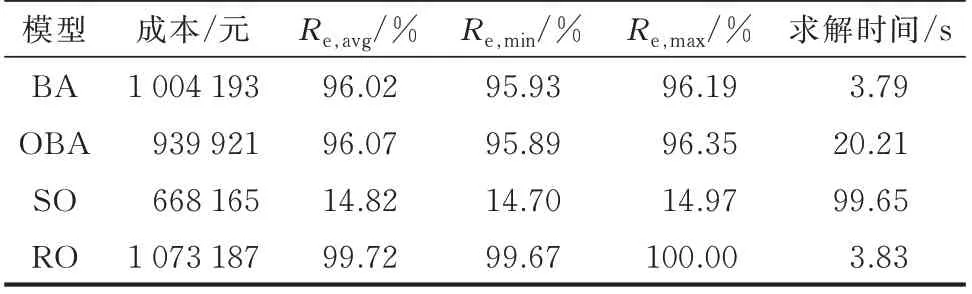
表2 IEEE 123 节点系统上不同模型的成本、可靠度和求解时间（ϵt=0.05）Table 2 Cost, reliability and solving time of different models with ϵt=0.05 on IEEE 123-bus system

表3 列出了模型在不同数量的EV 接入后的表现，结果表明计算时间随EV 数量增加较为缓慢，验证了模型对EV 数量有良好的可扩展性以及应对大规模EV 接入的潜力。

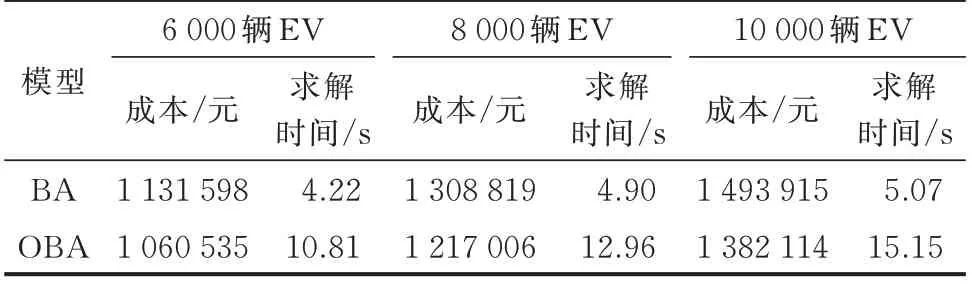
表3 IEEE 123 节点系统上不同数量EV 的结果Table 3 Results for different numbers of EVs on IEEE 123-bus system

4 结语

本文将考虑辅助市场的EV-配电网充放电调度问题建模为DRJCC 模型，以平衡运营成本和可靠性并克服经典SO 和RO 的缺点。然后，基于OBA 方法，将无法求解的联合机会约束转化为混合整数二次规划模型求解，与BA 方法不同的是，风险等级也被视为决策变量进行优化，降低了模型的保守性。最后，通过算例验证了模型平衡成本和风险的有效性、对EV 数量和更大电力系统的可扩展性。

本文研究未考虑拟合得到的随机变量概率分布与真实分布之间可能存在的偏差。未来，将进一步研究基于模糊概率分布的分布式鲁棒优化模型，并增加对光伏、风电、负荷、EV 充电行为等多维不确定因素之间的相关性研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。