基于动态自适应图神经网络的电动汽车充电负荷预测

张延宇，张智铭，刘春阳，张西镚，周 毅

（1.河南大学人工智能学院，河南省 郑州市 450046；2.河南省车联网协同技术国际联合实验室，河南省 郑州市 450046）

0 引言

在实施“碳达峰·碳中和”的目标背景下，电动汽车（electric vehicle，EV）作为一种使用可再生能源的交通工具，是推动国家能源清洁转型的重要方式之一［1］。然而，大规模EV 的无序接入造成所在区域电网负荷出现高波动性和高随机性等特点［2］，将会对电网造成潜在危险［3］。同时，给用电负荷预测任务带来了新挑战。对EV 充电站负荷进行精准预测不仅是研究电网负荷规划任务的基础［4］，而且是对EV进行充电引导的前提，对推动充电设施规划具有重要意义［5］。

目前，EV 充电负荷预测的方法主要分为基于统计学习的方法和基于机器学习（machine learning，ML）的方法［6］。统计学习方法主要利用统计分析技术对EV 充放电的历史数据进行建模和分析，预测未来的充电负荷［7］。文献［8］在考虑路网与电网之间的信息交互以及用户心理的基础上，预测了充电负荷的时空分布。文献［9］通过分析用户驾驶规律，采用蒙特卡洛模拟法建立了规模化EV 充电需求模型。文献［10］基于用户充电偏好、充电功率、充电位置等统计数据，建立了典型用户的概率出行模型。以上方法便于理解和实现，但普遍受到数据质量与样本数量的限制，充电负荷预测的精度难以保证。

随着人工智能（artificial intelligence，AI）技术的快速发展，ML 方法在充电负荷预测任务中应用日趋广泛［4］。文献［11］将卷积神经网络与长短期记忆模型结合，用于提取负荷数据的空间特征与时间特征以提高短期负荷预测精度。文献［12］利用长短期记忆神经网络和支持向量机等模型进行子序列充电需求预测，并通过堆叠集成学习策略综合考虑各模型预测的结果。文献［13］利用可学习的空间邻接矩阵构建图WaveNet 充电负荷预测框架。文献［14］利用小波分解提取可再生能源时序与频域信息，结合双向长短期记忆网络模型和注意力机制挖掘深层数据信息。文献［15］将图卷积网络与门控循环单元（gate recurrent unit，GRU）相结合，从而预测充电站的可用性。这些模型考虑到了不同充电站之间充电负荷的复杂时空依赖性，但是并未考虑不同充电站充电负荷波动大小对负荷预测精度的影响。实际上，大部分充电站的负荷波动较小，只有少数充电站负荷剧烈的波动才会影响电网平稳运行。

现有方法在捕获充电站负荷数据的长时序时间相关性（即输出与输入之间的长期依赖耦合关系）和空间相关性方面还存在不足，不利于提升长时序充电负荷的预测精度。文献［16］采用混合长短期记忆神经网络，单步预测精度可达99.99%，但预测步数增加至6 步时，精度下降至81.87%。基于此，本文提出一种基于数据驱动的自适应相关图模型，对隐藏在充电站负荷数据中的时空依赖性进行建模；然后，将自适应时空相关图与多头注意力机制相结合，使模型更关注于稀疏的重要充电站，以精准捕获其对负荷预测任务的影响；接着，利用图神经网络挖掘潜在的动态空间特性；最后，利用并行的多层时间卷积网络以扩大时间维度信息的感受范围，通过全连接层输出预测结果。

1 动态图神经网络的充电负荷预测框架

1.1 EV 充电负荷预测任务问题定义

本文使用图G=(Vg，Eg)表示充电站的图结构，其中，Vg为充电站节点集合；Eg为充电站之间边的集合。边的权重为2 个充电站负荷之间的相关强度。任意时刻t需要预测的充电站负荷参数都可以被视为图信号Xt∈Rd×L，其中，R为实数矩阵；d为节点数目；L为预测的充电站参数种类。本文只考虑预测未来的充电站负荷大小，故L=1。给定M个历史图信号Xt-M+1:t∈Rd×L×M，EV 充电负荷预测问题旨在学习函数f，从而预测未来T个时间步长的图信号Xt+1:t+T。

1.2 自适应相关图

由于实际中充电站分布具有稀疏性，少量重要充电站的波动对电网存在潜在威胁。站与站之间的连接随时间动态变化，仅通过静态的邻接信息并不能体现出充电站之间潜在的动态空间依赖关系。

式中:ν为波动的大小；Xt+1、Xt分别为第t+1、t时刻的充电站负荷参数。

图1 为50 个充电站第0 天到第11 天，即连续12 天的真实负荷数据热度图。7 号与8 号充电站在随时间变化的过程中，负荷量较高且ν变化剧烈。17 号充电站在第4 天到第5 天的ν也会对电网造成较大影响，而大多数充电站负载量随时间变化较为平稳，对电网的影响较小。

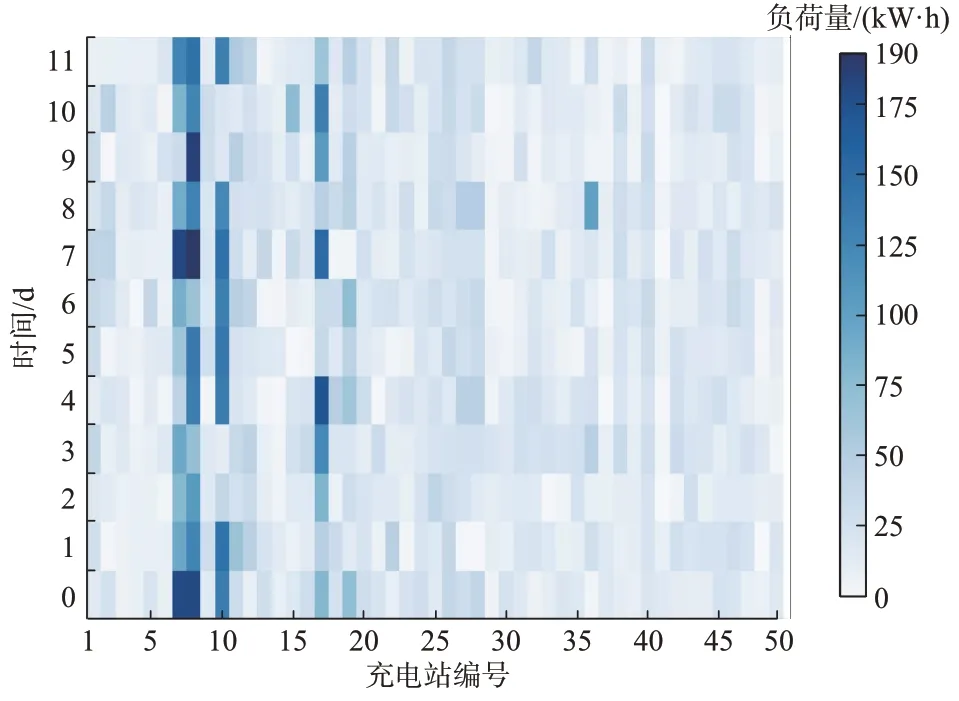
图1 充电站负荷数据热度图Fig.1 Heatmap of charging station load data

为了挖掘稀疏重要节点的潜在空间特征，本文采用可学习的自适应邻接矩阵学习充电站之间的空间依赖关系。通过随机梯度下降法，模型自动学习每个充电站在空间与其他充电站之间的连接权重。

式中:E1、E2为可学习参数；d为节点数目；归一化指数函数softmax(·)、线性整流函数（rectified linear unit，ReLU）Re LU(·)为激活函数；Rd×Pa为d行Pa列的矩阵；Pa为节点嵌入的超参数。为了捕获重要节点的动态变化，本文在自适应邻接矩阵的基础上，选取每行权重最大的值，并通过设置超参数Ps 用来选取每天中重要节点的数量，建立自适应相关图矩阵，并将其余节点全部设置为0。空间注意力层如附录A 图A1 所示。本文将作为多头注意力机制的先验知识输入，并作为空间注意力层的值V，通过学习空间维度充电站分布对时间维度负荷信息的影响以动态调整模型参数。同时，设置一个可学习的参数Wm，j，以控制空间维度对时间维度信息的影响。

1.3 动态自适应图神经网络充电负荷预测框架

基于动态自适应图神经网络的充电站负荷预测算法框架如图2 所示。框架由4 部分构成，分别为数据处理层、充电负荷信息时空关联特征提取层、充电负荷信息时空卷积层和输出结果层。

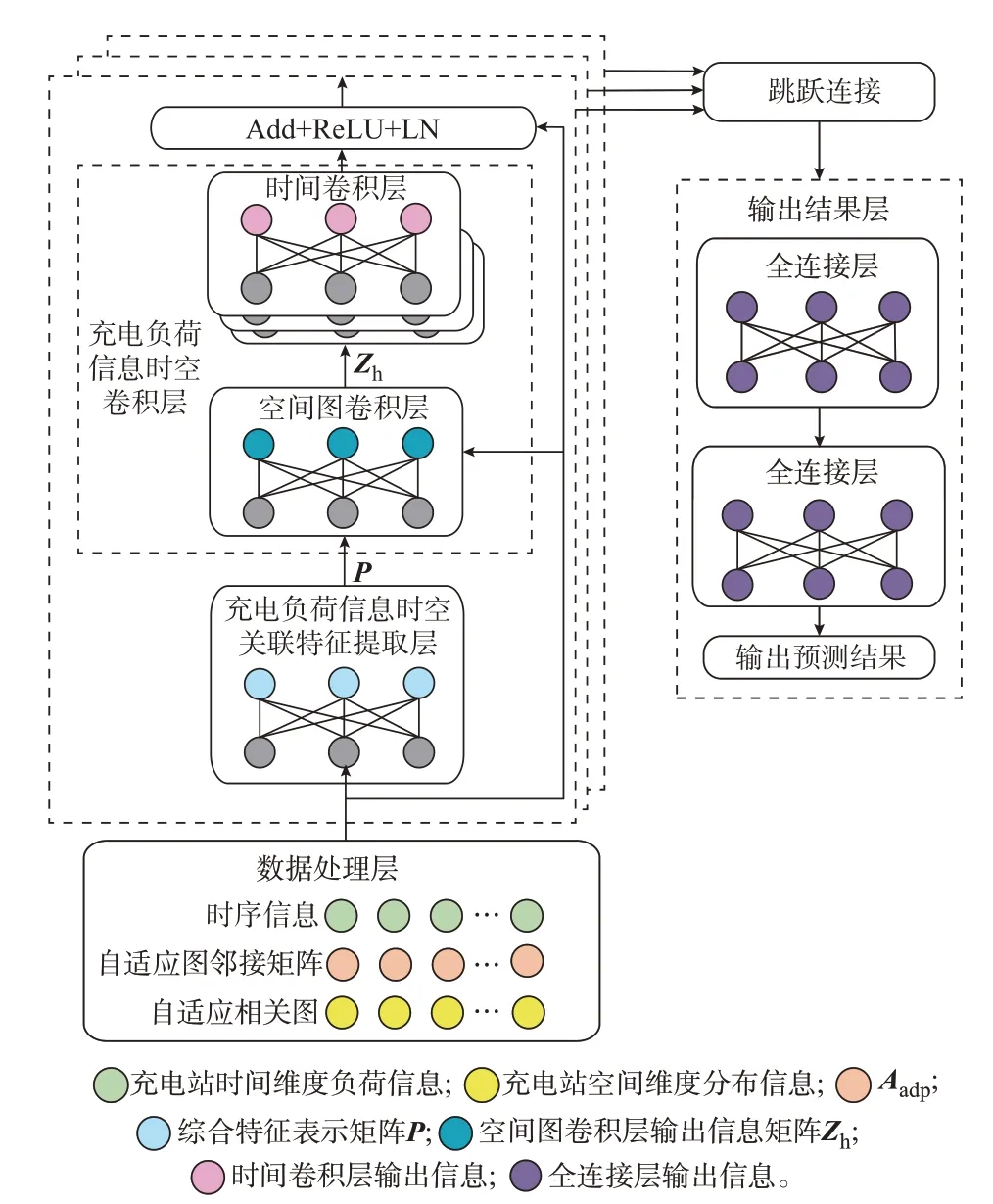
图2 基于动态图神经网络的充电负荷预测框架Fig.2 Framework of electric vehicle charging load prediction based on dynamic graph neural network

数据处理层的时序信息由充电站负荷量构成，自适应图邻接矩阵通过算法自动学习获得，表示不同充电站负荷之间的空间相关性，自适应相关图用于刻画重要的少数波动节点。通过多头注意力构成的时空关联特征提取层，将充电负荷历史数据转换为具有时空关联性的综合特征表示。充电负荷时空卷积层由空间图卷积层和时间卷积层组成，用于综合考虑时间和空间之间的关联性。将时空特征提取层的输出相加（addition，Add）、经过激活函数Re LU(·)并取自然对数（natural logarithm，LN）进行整合输入到下一层网络中。将多层网络通过跳跃连接以获取不同时间层上的空间依赖关系，最后，经过2 个全连接层输出预测结果。

2 充电站负荷信息时空关联特征提取层

2.1 多头注意力机制

多头注意力机制可以有效提取负荷序列信息之间的依赖关系，广泛应用于深度学习领域［17］。在充电负荷预测任务中，利用该方法能够有效捕获充电负荷的变化趋势等多种不同的重要特征，生成更全面的充电负荷特征表达式［18］。多头注意力机制的并行化处理能力为解决充电负荷任务的动态时空变化以及长时序任务的特征信息提取，提供了有效的解决方案［19］。

注意力机制模型见附录A 图A2。将输入信息X线性映射为查询矩阵Q、键矩阵K、值矩阵V。

式中:Wq、Wk、Wv分别为用于映射查询、键、值的权重矩阵。通过学习这些权重矩阵，模型可以根据任务的需求，自适应地调整输入序列不同映射空间中的表示。将Q与K进行点积操作并除以计算注意力得分，以衡量查询对于键的注意程度。

式中:dk为矩阵K的维度；Iatt(·)为计算注意力权重矩阵的函数。

多头注意力机制为获取不同子空间的特征信息Bhead，r，将输入序列映射R次，如式（6）所示。

式中:Wq，r、Wk，r、Wv，r分别为第r个头的查询、键、值的权重矩阵，均为可学习的参数。

然后，通过将所有的输出Bhead，r拼接在一起以聚合不同子空间的特征信息矩阵O，如式（7）所示。

通过多个注意力头的并行计算捕获充电负荷信息在不同时间尺度上的相关性，从而捕获EV 充电负荷的短时间尺度突变和长时间尺度上的周期性波动趋势。

2.2 基于多头注意力机制的时空关联特征提取层

不同于传统负荷预测模型直接将充电负荷的时间序列信息输入模型，本文构建基于多头注意力机制的时空关联特征提取层。在时间注意力层中，利用多头注意力机制建立长时序之间的耦合关系，每个注意力头分别捕获不同子空间的信息，以提高模型的表达能力。

设X为多头注意力模块的输入，对于每层的注意力，都有独立的权重矩阵进行线性变换。对于第l层，根据式（4）定义以下参数:XWq，l=Ql，XWk，l=Kl，XWv，l=Vl。根据式（5）计算第l层的注意力，如式（8）所示。

式中:Ql、Kl、Vl分别为第l层的查询、键和值矩阵；Al、Al-1分别为l层、l-1 层的注意力得分，其关系如式（9）所示。

为缓解梯度消失问题，以及信息更好地在网络中传递与更新，本文利用剩余注意力的概念，在保留本层计算出的注意力权重的基础上［20］，加入上层特征A l-1，以提升特征的表达能力和模型的训练效果。

为获取不同子空间信息，将Ql、Kl、Vl分别映射R次，然后，通过式（6）计算每个注意力头的值，如式（10）所示。

根据式（7）得到将每个注意力头合并后的输出O。将输出结果O与原始输入X相加并经过一个全连接层后，输出zs，并进行层归一化，得到z～s如式（11）所示。

式中:μs、σs分别为该层的均值、方差；⊙为哈达玛积；γ、β分别为缩放、平移的参数向量；ε为较小常数，防止分母为0。

试验地设在贵州省威宁县雪山镇雪山村，地理位置E 104°17′，N 26°52′，海拔1 937 m，年平均气温为10.8℃，极端最高气温为31.5℃，极端最低气温为-7.1℃，最热月平均气温17.1℃，最冷月平均气温3.5℃，≥0℃年积温3 645℃，年降水量859.4 mm，降水多集中在5～9月，占全年降水量的80 %。无霜期202.4 d，年日照时数1 635.2 h，相对湿度79%，供试土壤(0～30 cm)的理化性质为有机质5.71 g/kg，碱解氮36.65 mg/kg，速效磷21.87 mg/kg，速效钾104.17 mg/kg，pH 7.3。

充电负荷信息时空关联特征提取层如图3 所示。

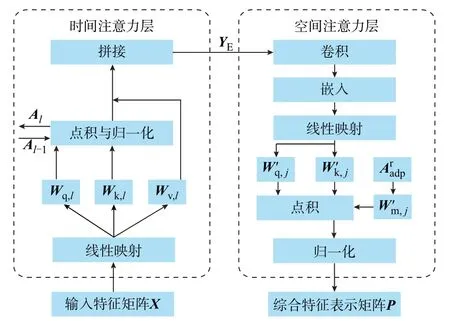
图3 充电负荷信息时空关联特征提取层Fig.3 Spatiotemporal correlation feature extraction layer for charging load information

式中:P为动态综合特征表示矩阵。

3 充电负荷信息时空卷积层

3.1 空间特征卷积网络

传统的图卷积网络一般采用预定义的静态图结构，但面对稀疏度较高的充电站分布时，传统的邻接矩阵无法有效地捕获到充电站之间的空间依赖关系，导致充电负荷预测模型不准确。为了更好地捕捉充电站之间的空间依赖关系，将自适应邻接矩阵与切比雪夫多项式图卷积网络结合。利用自适应邻接矩阵动态地学习节点之间的依赖关系，切比雪夫多项式图卷积通过在多项式中增加时间步长的方式，对动态图结构进行建模与学习，更好地挖掘节点之间的特征信息［21］。

k阶切比雪夫多项式Tk参数化的切比雪夫卷积核如式（15）所示。

式中:Λ为对角矩阵；θk为多项式系数；K为切比雪夫多项式的最高阶数。

对于综合特征表示矩阵P，应用切比雪夫卷积核的过程如式（16）所示。

式中:U为由图G的拉普拉斯矩阵的特征向量组成的矩阵；Zh为第h层时间序列信息矩阵。

3.2 时间特征卷积网络

传统时间卷积由于卷积核大小的限制，针对充电负荷预测任务，只能捕获固定长度的时间序列信息，限制了对不同时间尺度信息的捕获能力。设输入的时间序列信息矩阵为Zh，卷积核为Γ∈R1×S×L×2L，通过卷积核提取的信息为=，在时间维度捕获的信息为=φ(E)⊙σ(F)。式中:为门控单元操作后得到的卷积核；φ(·)为激活函数；E、F分别为负荷时间序列的前半部分、后半部分。其卷积核通常只能捕获单个局部的时序信息，无法充分捕获时间维度的充电站负荷信息。针对这一问题，本文采用多尺度因果卷积模型［21］，见附录A 图A3。利用多个不同卷积核的门控卷积单元，并行处理时序信息。首先，通过不同卷积核对输入信息进行卷积操作，将输出结果进行池化后，得到多个不同的聚合特征ϒi。将不同卷积核中获得的特征拼接起来，得到多层门控卷积单元，从而捕获不同维度的时间特征信息。为了防止信息的丢失，再将拼接后的特征信息与初始输入信息相加，然后经过激活函数后，输出Zout，h，如式（17）所示。

4 算例分析

4.1 数据分析与处理

为验证本文所提算法的性能，利用Dundee 数据集［22］与Palo Alto 数据集［23］中的EV 充电负荷数据集进行算法验证，这2 个数据集分别包含50 个充电站与35 个充电站。附录A 表A1 为各算法运行效率。附录A 图A4 是从Dundee 数据集中任意选取的3 个充电站的负荷曲线。在数据处理阶段，首先，通过归一化处理将数据缩放到0 到1 范围；其次，将原始数据中超出3 倍标准差的异常数据点剔除。选择数据集中的全部数据，按照6∶2∶2 分为训练集、验证集和测试集。

设置多头注意力的头数H=3。输入长度为12 d 的历史负荷数据，预测未来12 d 的负荷数据。堆叠3 个时空层，节点嵌入E1、E2大小设置为10，并对其进行随机初始化，切比雪夫多项式的K设置为3。时间卷积层维度分别设置为3、5、7，扩散步骤设置为3，学习率设置为0.001。模型在2 个数据集上分别训练3 000 轮，其中，在1 000 轮和2 000 轮时，对学习率进行动态调整分别再乘0.9，批量大小为32。

4.2 算例结果分析

为了验证本文所提算法的有效性，将其预测结果与2 种传统时间序列预测算法和3 种基于深度学习的基准算法进行了对比。其中，3 种深度学习算法分别为循环扩散卷积神经网络（diffusion convolutional recurrent neural network，DCRNN）算法［24］，图WaveNet 算法［25］和自适应时空图神经网络（adaptive spatio-temporal graph neural network，Ada-STNet）［17］算法。采用统一优化函数，以验证本文算法的有效性。在Dundee 数据集上随机选取一个充电站的12 d 负荷数据进行预测，如图4 所示。

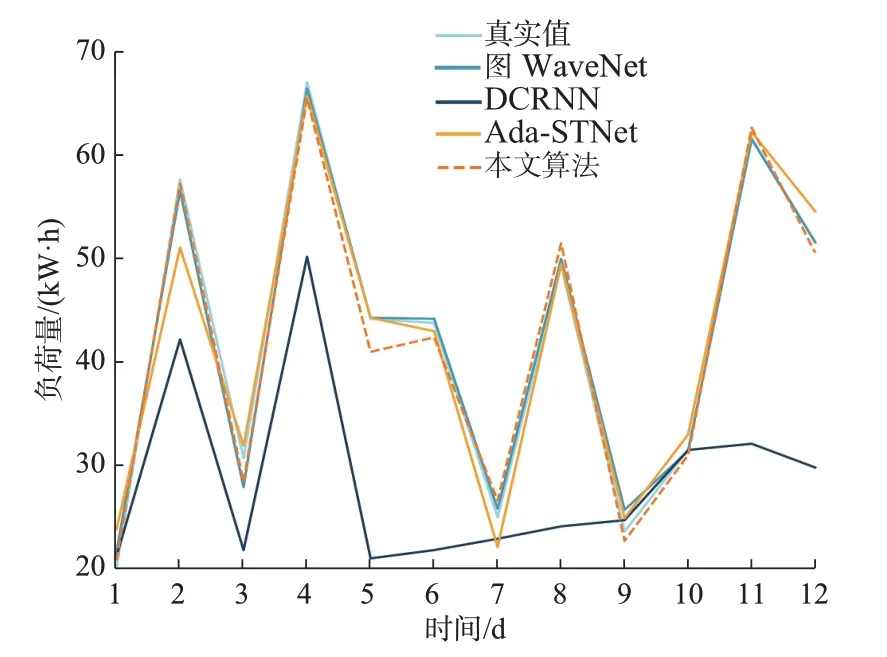
图4 Dundee 数据集预测结果Fig.4 Prediction results on Dundee dataset

由图4 可以看出，DCRNN 算法相较于其余3 种算法，由于难以建立长时序之间的耦合关系，模型预测效果与真实值之间的误差随时间的增加越来越大。对于本文算法，在9～11 d 期间，负荷量在23.5 kW·h至61.6 kW·h 之间连续波动。本文算法对于较大的波动感知能力相较于其余3 种算法更强，预测结果最为精准。这验证了多头注意力机制与时空相关图结合针对长时序任务以及对于重要节点捕获的有效性。

如附录A 图A5 所示，在Palo Alto 数据集上，图WaveNet 虽然在Dundee 数据集表现较好，但随着数据量的增大，导致时空复杂性提高，预测精度在Palo Alto 数据集有明显下降，本文算法依旧可以捕获到较大波动趋势。在7 d 时负荷从23.5 kW·h 突变为91.3 kW·h，本文算法相较于其余算法依旧可以达到最接近的预测值。

为验证本文算法可以有效捕获少数重要节点的波动情况，将波动分为4 种情况进行实验验证，分别为:0 ≤ν＜1、1 ≤ν＜2、2 ≤ν＜3、ν≥3，对于每种波动情况选取不同充电站，用筛选出的6 个位置进行预测，如附录A 图A6 至图A9 所示。在附录A 图A9 第5 组数据中，即使ν≥30，本文算法依旧可以达到最低误差7.60%。对于0 ≤ν＜1 的情况，本文算法的每个点的预测误差值相较于其余算法大多数可以保持最低。

将所有波动情况进行评估并取平均值，如图5所示，将较于其余算法随着波动的增加本文算法的误差率保持相对平稳，能够精准预测较大波动的负荷变化情况。对于图WaveNet 算法，3 倍以上波动的预测误差达到了30%以上，而本文算法依旧可以保持在15%以内。Ada-STNet 算法虽然在2 ≤ν＜3 与ν≥3 这2 种情况下预测误差相较于1 ≤ν＜2的情况有所下降，但依旧高于本文算法的预测误差。

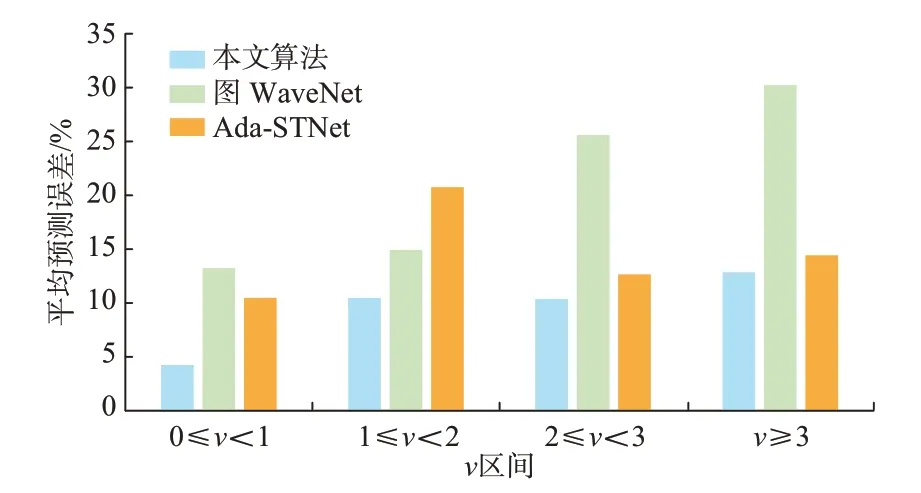
图5 波动点预测误差Fig.5 Prediction error at fluctuation points

如附录A 图A10 所示，任意选取一组数据用热度图表示输入网络的初始负载情况。附录A 图A11反映出初始随机赋予的时空关联性综合特征的权重。经过第1 次时空关联特征提取层后的输出情况如附录A 图A12。第1 次迭代后可能受到初始权重的影响，模型重点关注于23 号充电站，但再次迭代后，如附录A 图A13 所示，模型不再重点关注23 号充电站，模型更关注于1 号充电站与5 号充电站，也与真实输入情况有一定的相似性。结合上述实验说明了自适应相关图与多头注意力机制的结合使模型可以有效地捕获少数重要节点的波动情况。

为了进一步验证本文所提出算法的有效性，以所有充电站预测结果的平均绝对误差（mean absolute error，MAE）IMAE、平均绝对百分比误差（mean absolute percentage error，MAPE）IMAPE、均方根误差（root mean square error，RMSE）IRMSE为评价标准，将本文算法与多种基准算法进行了对比，如表1 和表2 所示。表中:“本文算法-A”表示多头注意力机制中不加入自适应相关图的预测模型。

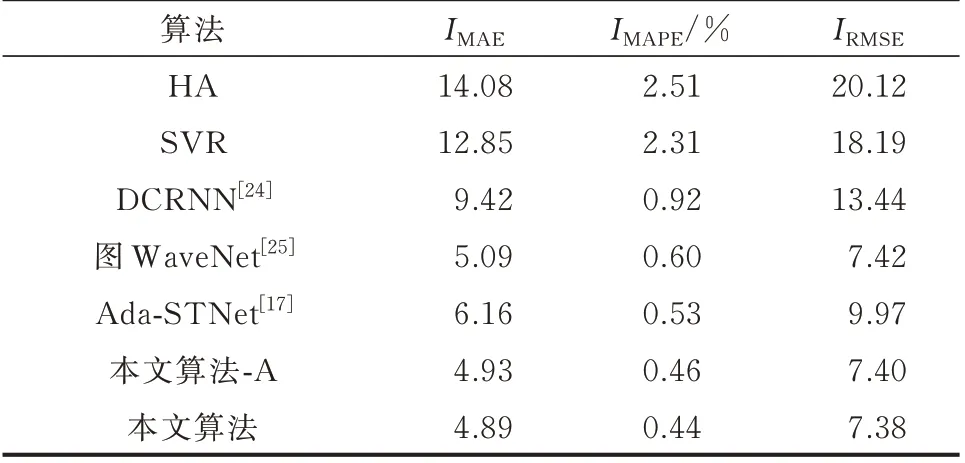
表1 Palo Alto 数据集预测误差对比Table 1 Comparison of prediction error on Palo Alto dataset

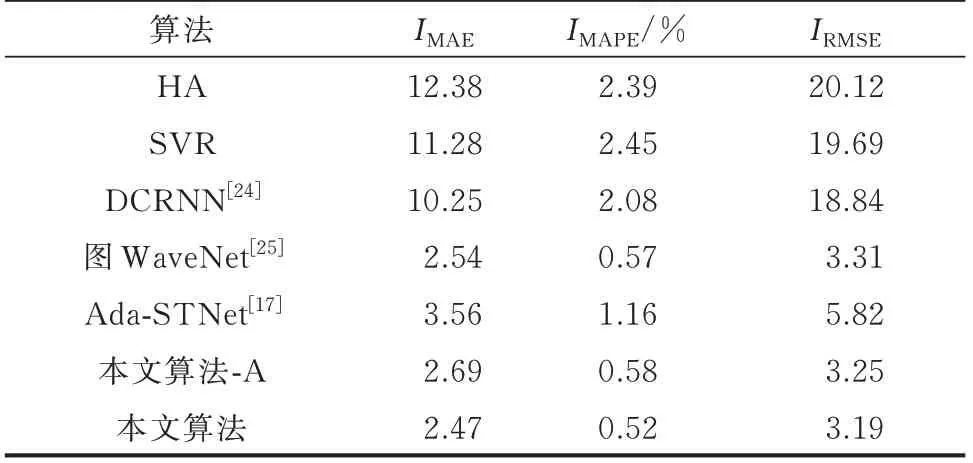
表2 Dundee 数据集预测误差对比Table 2 Comparison of prediction error on Dundee dataset

在以IMAE指标下，统计学方法的历史平均（historical average，HA）法与ML 方法的支持向量回归（support vector regression，SVR）法误差相对较高，可能是2 种方法通常假设充电负荷数据具有平稳性，无法充分捕获到充电负荷的复杂性与时空特性。对于DCRNN 算法，可能在处理噪声和波动性方面的能力相对较弱，无法准确预测充电负荷，从而出现较大的误差。然而，通过引入多头注意力机制与自适应相关图结合的方式，本文算法能够有效地捕获少数重要充电站之间的空间依赖关系，从而提高预测的准确性。与现有的先进方法，如Ada-STNet 和图WaveNet 进行对比，本文算法在Dundee数据集与Palo Alto 数据集上的IMAE分别为4.89 与2.47，相较于其他算法误差均为最低。相对于Ada-STNet，本文算法通过加入自适应相关图等创新机制，更好地利用了节点属性来引导优化图结构，并通过时空卷积框架来捕获复杂的时空关联性。相对于图WaveNet，自适应相关图结合多头注意力机制能够更好地建模充电负荷的动态特征。这些改进使得本文算法在2 个数据集上都取得了较低的预测误差，证明了其在充电负荷预测任务中的有效性。

为了进一步验证模型中加入自适应相关图模块的有效性，进行了消融实验。加入自适应相关图模块后，在2 个数据集上无论是哪个评价指标，本文算法都得到了提升。以Dundee 数据集上IMAE指标为例，加入自适应相关图模块后，本文算法的预测误差又降低了8.18%。消融实验结果表明，通过自适应相关图与多头注意力机制的有效结合，模型能够更准确地捕捉充电负荷数据中的时空关联性和动态特征，从而提升预测性能。同时，研究了超参数Ps的取值对预测精度的影响，结果如附录A 表A2 所示。实验结果表明，随着Ps取值的不断增加，预测精度逐步下降，证明了自适应相关图通过关注少数重要节点可以有效提升算法的预测精度。

5 结语

针对具有复杂时空耦合特性的EV 充电负荷预测任务，本文通过将自适应相关图与多头注意力机制结合的方式，生成了负荷数据的综合时空特征表达式，使模型能够捕获具有高波动性的少数关键充电站节点。利用切比雪夫多项式图卷积与多尺度时间卷积层，通过多种层级特征提取，学习不同子空间中的时空信息，可以有效挖掘充电站的动态时空特征，捕获到长时序之间的耦合关系，从而提高充电负荷预测的准确性与稳定性。

在2 个真实数据集上的实验表明，本文所提算法在面对负荷数据的较大波动和较长时序任务预测时，仍然能够得到令人满意的预测结果，并且算法的稳定性和鲁棒性强。后续工作将研究极端天气和突发状况对负荷预测精度的影响，并以负荷预测结果为基础，研究充电基础设施的最优规划问题。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。