基于岭回归改进规范变量分析的微震事件实时判识

程健，石林松，骆意，周天白，杨凌凯

（1.煤炭科学研究总院，北京 100013；2.煤炭科学研究总院有限公司 矿山大数据研究院，北京 100013；3.天地科技股份有限公司，北京 100013；4.煤炭智能开采与岩层控制全国重点实验室，北京 100013）

0 引言

加速煤矿智能化发展，建设数字化、智能化矿山和绿色煤炭工业新体系，实现煤炭资源的安全开发利用，是我国煤炭工业新时期高质量发展的战略任务[1]。随着我国煤矿采深逐年增加，各类安全监测系统已成为保障煤炭安全生产的重要组成部分。其中微震监测系统作为一种区域性、实时、连续的监测系统，可对各类震动信号进行实时采集分析，广泛应用在煤矿安全监测领域[2]。

在微震监测中，微震事件判识是一项重要的基础工作，也是进一步开展震源位置与震级能量分析等工作的基石。众多学者依据微震特性进行微震事件判识研究，形成了震源参数分析、震动波波速层析成像技术等理论[3]。文献[4]基于数据驱动思路，对离线微震监测数据进行特征提取，并对特征数据进行半监督非平衡学习，解决了不平衡微震数据集的识别问题。文献[5]利用流形学习的非线性降维思想，提出了一种流形嵌入过采样方法，为有机结合流形学习与过采样的非平衡数据模式分类方法提供了框架，对于较大规模的非平衡微震数据有稳定的分类效果。在现场应用中，以动载应力集中系数[6]等指标辅助的监测方式是主流，如KJ768 监测系统、ARAMIS 监测系统，其通过对近期数据的统计划定阈值，进而判断微震事件危险等级[7]。文献[8]通过分析微震数据时空演化规律，认为综合分析微震历史事件平均数、平均释放能量、地震参数等可提升微震事件预测精度。

实际工程数据中存在大量干扰信号和噪声，导致微震事件实时判别易产生错误结果，主要原因是常规的微震监测技术大多基于单物理量变化规律而开发[9]。因此，充分融合多通道微震信号，得到准确且鲁棒的分析结果，是微震事件实时判识的关键。状态监测与判识方法可对多通道信息进行融合分析，从系统稳定性的角度为多通道微震信号融合分析提供了可能[10]。其核心原理是采用多元统计分析与数据挖掘方法，对传感器采集信号进行分析并挖掘潜隐空间信息，得到系统稳定性的度量[11]。常用的状态监测与判识方法包括主成分分析（Principal Components Analysis，PCA）[12]、偏最小二乘（Partial Least Squares，PLS）方法[13]、规范变量分析（Canonical Variate Analysis，CVA）[14]，其中CVA 对时序数据的处理效果较好，更适用于动态数据场景[15]。为进一步提高CVA 的信号处理能力，有学者对其进行改进，提出了多模块方法和核函数方法等[16-20]，通过高维空间分类对非线性数据进行有效挖掘，但抗噪声干扰能力仍较差。对此，文献[21-23]将稀疏化建模引入CVA，以应对噪声干扰。鉴于多通道微震监测信号具有强自相关性和互相关性[4]，上述方法用于微震事件判识时存在误判情况。本文采用稀疏化建模中的岭回归方法改进CVA，通过模拟实验和实际微震监测数据验证了该方法的有效性。

1 CVA 与稀疏化建模原理

CVA 通过最大化2 个变量集间的相关度，实现对高维数据的降维[24]。其优势在于通过处理数据之间的相关性来提高数据的辨识度，有利于提高训练模型的监测效果。

设给定2 组向量x∈Rm和y∈Rn，m，n为向量维度，x和y的协方差矩阵分别为 Σxx和 Σyy，互协方差矩阵为 Σxy，矩阵J∈Rm×m和L∈Rn×n满足以下条件：

式中：I为前个对角元素为1、其余对角元素均为0 的对角矩阵，=rank(Σxx)；I为前个对角元素为1、其余对角元素均为0 的对角矩阵，=rank(Σyy)；D为规范相关系数矩阵；ωi为规范相关系数，i=1，2，…，r，r为规范相关系数矩阵D的秩。

设存在向量c，d，其中c=Jx，其协方差矩阵Σcc=JΣxxJT=I，d=Ly，其协方差矩阵Σdd=LΣyyLT=I，c和d之间的互协方差矩阵为规范相关系数矩阵D，即 Σcd=D=diag(ω1,ω2,···,ωr,0,0,···,0)。

c和d的相关程度可由规范相关系数表示。映射矩阵J，L及规范相关系数矩阵D可通过奇异值分解方法计算：

CVA 将过去和未来的信息分离，在特定时刻t（t∈{K+1,K+2,···,N-K+1}，K为观测长度，N为观测样本数），包含过去信息的向量pt与包含未来信息的向量ft分别为

通过将过去信息和未来信息构造为过去与未来矩阵并应用于CVA 中，可得到样本估计下的状态空间模型。由于煤矿微震监测信号包含大量噪声干扰，所以信号估计模型的输出值与实际值存在偏差。可采用稀疏化建模降低噪声信号干扰，以获得更准确的估计模型。稀疏化建模通过降低干扰信息和噪声在估计模型中的权重，有效保留微震监测数据中的重要信息。岭回归是一种可用于共线性数据的有偏估计回归方法，是经典的稀疏化建模方法之一。其通过在损失函数中加入正则项，使回归系数接近0，从而实现稀疏化，避免过拟合现象，提升模型泛化能力，对含强噪声、大干扰数据的拟合性能优于常见的最小二乘法。

2 岭回归改进CVA

2.1 岭回归改进CVA 原理

微震监测系统包含多通道监测信号，实现对不同区域的实时监测。利用微震监测信号时间序列构建pt和ft，组合为过去信息矩阵X和未来信息矩阵Y：

CVA 目标函数为

式中u，v分别为U和V的列向量。

采用岭回归算法改进CVA 的损失函数，得到新的损失函数：

式中 λ1,λ2为收缩参数。

式（8）可等价为

构造Lagrange 函数并简化，得

式中 β1，β2为Lagrange 乘子。

对u，v分别求偏导，并令导数为0，即

求解式（11），得

式中I为单位矩阵。

上述模型的伪代码如下。

2.2 岭回归改进CVA 判识方法

依据Hotelling-T2检验定理计算统计量和。

式中：k为选取的规范变量空间维数，本文中k=K；Fα(·)为F 统计检验函数；α为置信度；q为剩余空间维数，本文指噪声空间维数。

根据岭回归改进CVA 得到的u中前k行元素组成的向量uk和后q行元素组成的向量uq计算监测量

3 实验验证

通过模拟实验及基于实际微震监测数据的实验验证岭回归改进CVA 的有效性和正确性。

3.1 评价指标

采用平均准确率CAC、误报率RFP、漏报率RFN和错误率RE作为数据判识评价指标，取多次实验的平均值。

式中：TP 为将异常点判识为异常点的个数；TN 为将正常点判断为正常点的个数；FP 为将正常点判识为异常点的个数；FN 为将异常点判识为正常点的个数。

3.2 模拟实验

采用文献[25]中的模拟数据构造方法，验证岭回归改进CVA 的判识效果。用于训练的每个正常数据集包含2 500 个观测数据、16 个特征，每个测试集包含2 500 个观测数据、16 个特征。每个数据集均在没有异常波动的情况下开始生成，测试集在第1 500 次观测后触发异常波动。每个数据集分为A、B两部分，特征个数分别为3、13，特征生成规则如下。

式中：g1（t）—g13（t）为白噪声序列，可自行设置均值和方差；θ为故障系数，用于改变测试集数据的波动程度。

设置正常数据集中 θ=0，测试集中t=1 500 之前θ=0，之后 θ≠0。令t0为数据波动开始时刻，即t0=1 500，则 θ设置规则为

模拟数据集生成方法：①预先生成白噪声序列g1（t）—g13（t），其均值为0，方差自行设置。②从{1,-1}中随机生成观测数据A。③利用A生成数据B，其中t=1 500 时刻改变故障系数 θ，构造波动数据。训练集和测试集数据分别如图1（a）和图1（b）所示，其中8，9，16 号通道分别为A1，A2，A3，其他通道依次为B1—B13，3，12，13，14，15 号通道在t=1 500 时刻之后因θ 改变而发生波动，红色部分为t=1 500～2 500时刻。

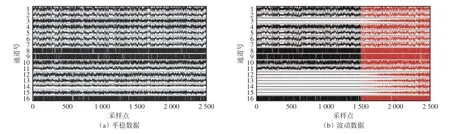
图1 训练集与测试集数据Fig.1 Data in training set and testing set

经多次实验验证，式（12）中包含的4 个可调参数λ1,λ2,β1,β2均设置为1，置信度 α=99%。

生成9 组不同噪声方差下的数据，每组噪声方差下分别采用CVA 和岭回归改进CVA 进行3 次判识实验，结果如图2 所示。可看出随着噪声方差由5×10-6增大至 5×10-2，岭回归改进CVA 的判识准确率较CVA 提升了0.6%～5.4%，误报率和漏报率之和较CVA 降低了4.8%～17.3%。可见岭回归改进CVA 具有较好的鲁棒性，在噪声干扰下具有较高的异常判识准确率。

图2 模拟数据实验结果Fig.2 Experiment results by simulation data

3.3 基于实际微震监测数据的实验

采用煤矿微震实际监测数据验证岭回归改进CVA 的应用效果。微震监测数据由波兰SOS 微震监测系统采集，每个数据集包含20 个通道监测数据，每个通道数据包含10 240 个采样点。实验中使用的微震信号测试集包含3 组平稳状态数据集（测试集1，2，3）和3 组波动状态数据集（测试集4，5，6）。以测试集4 为例进行判识，其各通道微震监测数据如图3 所示。

图3 微震监测数据Fig.3 Monitored microseismic data

通过岭回归改进CVA 融合分析测试集4 中20 个通道的微震监测信号，采用99%置信度，设置λ1,λ2,β1,β2均为1。微震判识结果如图4 所示，蓝色线代表融合分析的监测量，红色线代表统计量，若大于，则判断该时刻发生微震信号波动，即发生微震事件。从图3 可看出，20 个通道未全部监测到微震信号波动，但由于多通道信号间的相关关系已发生改变，经岭回归改进CVA 融合分析的结果反映出微震监测信号处于波动状态，验证了岭回归改进CVA 具备微震事件实时判识功能。

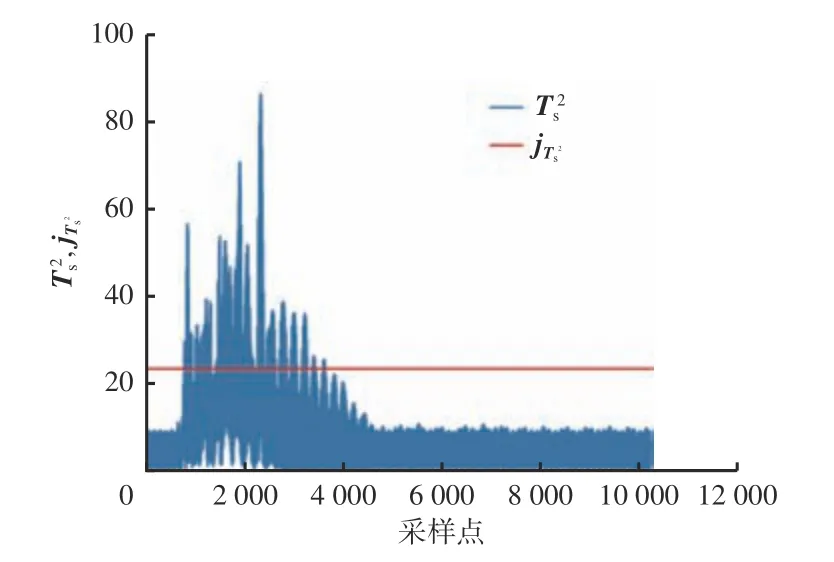
图4 微震监测数据融合分析统计结果Fig.4 Statistics of fusion analysis of monitored microseismic data

采用6 个测试集对岭回归改进CVA 与CVA 的判识性能进行验证，结果见表1。可看出岭回归改进CVA 的平均准确率为97.14%，较CVA 高2.39%，误报率与漏报率之和较CVA 降低了0.07%。

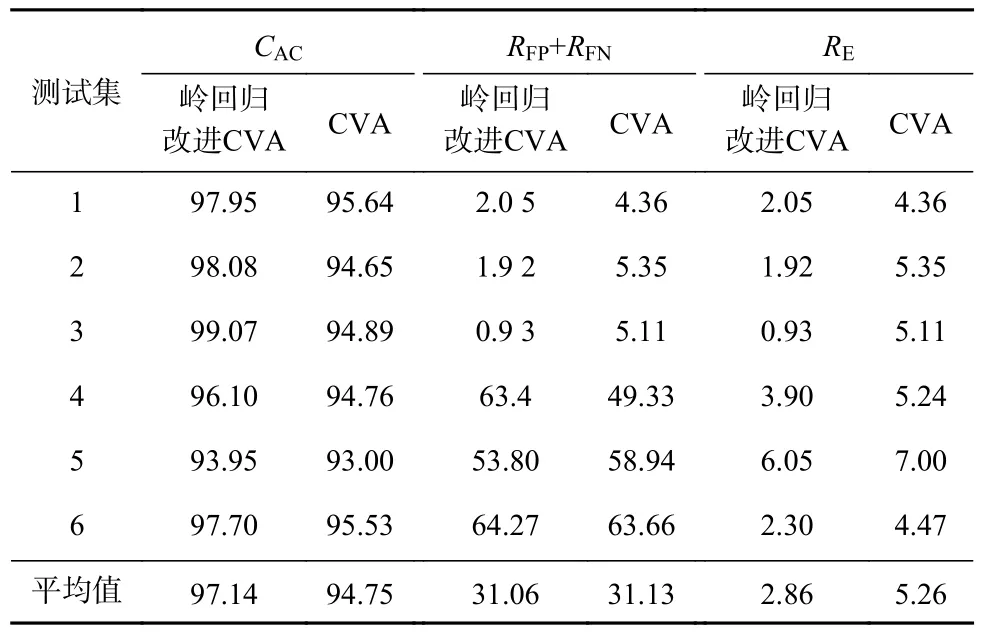
表1 微震数据实验结果Table 1 Experiment results by microseismic data %

4 结论

1）针对含有噪声和干扰信号的煤矿微震监测信号，采用岭回归改进CVA 对多通道微震信号进行融合分析，进而实时判识微震事件。

2）采用模拟数据和实际微震监测数据对岭回归改进CVA 进行实验验证，结果表明，对于含噪声和干扰信号的微震监测数据，岭回归改进CVA 较CVA 具有更优的判识能力。

3）下一步将针对噪声环境，构造基于信噪比改变通道信号权重的稀疏化模型，以优化岭回归改进CVA 对多通道微震信号的自主筛选能力。