水力喷砂射孔喷嘴研究
2024-04-22王世强王星刘景超郝宙正张玺亮
王世强,王星,刘景超,郝宙正,张玺亮
(中海油能源发展股份有限公司 工程技术分公司,天津 300452)
0 引言
水力喷砂射孔技术是20世纪90年代末发展起来的,目前国外应用比较广泛的技术,与常规的聚能弹射孔技术相比,流体喷砂射孔技术不存在压实带,而且射孔的孔径大、穿透深,被广泛应用于低孔低渗油气藏的开采。水力喷砂射孔的主要技术原理是:含砂(磨料)的流体通过地面加压设备和井下喷砂射孔喷嘴将高压流体的压力势能转化为流体动能,使喷嘴出口的流体达到每秒上百米甚至几百米的速度,同时带动磨料射向套管,高速运动的磨料撞击套管壁后形成微切削作用,逐渐射穿套管、水泥环后,水射流冲击地层,形成纺锤状的通道,最终达到增大地层泄流面积的目的[1-2]。
因此,喷砂射孔喷嘴是整个射孔技术的关键所在,在同样的地面设备条件下,好的喷嘴可以更好地将流体压力势能转化为动能,提高喷嘴出口流体及砂粒的横向速度,增强穿透套管能力。同时,喷嘴自身须具有良好的耐冲蚀性,以保证井下喷砂射孔的作业寿命。
1 喷嘴参数计算
描述射流喷嘴特征的基本参数主要有流体压力、功率、流速、流量、反冲力等动力学参数[3]。
如图1所示,对于连续射流模型,在射流喷嘴入口和出口处两点利用伯努利方程和连续性方程,假设壁面光滑,忽略沿程阻力及高度差,可得出如下关系式:
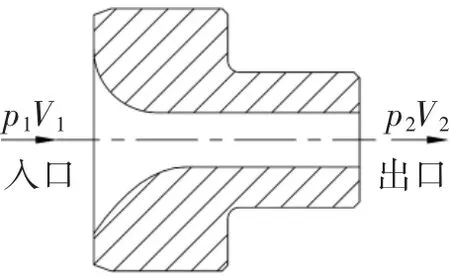
图1 喷嘴内截面示意图
式中:p1、p2分别为喷嘴入口和出口处的静压力,V1、V2分别为喷嘴入口和出口处的平均流速[4]。

由于喷嘴流道为圆管型结构,则有,并假设ρ1=ρ2,则由式(1)和式(2)可得
由于高压射流过程中,p1>>p2,d2/d1<<1,同时将ρ=998 kg/m3代入式(1)~式(3),最后得出流体射流流速简化表达式:
式中:Vt为射流流速,m/s;p为喷嘴入口压力,MPa;qt为射流流量,L/min;d为喷嘴出口直径,mm。
由式(4)和式(5)得出的是理论流量和流速,通过喷嘴的实际流速v和流量q要比该值小。
当射流流量和喷嘴入口压力确定后,就可以计算喷嘴的射流功率:
将式(5)代入整理可得
式中,P为射流功率,W。
2 喷嘴结构优化
根据收缩段形式的不同,目前常见的成熟喷砂射孔喷嘴有锥直型、圆弧型、抛物线型3种,如图2~图4所示。

图2 锥直型喷嘴
图3 圆弧型喷嘴
图4 抛物线型喷嘴
在相同的工作参数下,判断喷嘴性能好坏的参数为砂粒出口速度和冲蚀率:砂粒出口速度越高,喷嘴的切割性能越强;冲蚀率越低,喷嘴使用寿命越长。
2.1 喷嘴切割性能分析
2.1.1 求解控制[5]
1)求解器的选择。
选用二维稳态隐式求解器,湍流方程采用标准k-ε模型,欧拉两相流模型,SIMPLE算法,动量方程采用二阶迎风格式,体积分数采用一阶迎风格式。
2)边界条件的设定。
a.入口边界条件。入口为速度入口,速度大小为15.8 m/s,入口流量为197 L/min,砂粒体积分数为0.08,砂粒直径为0.3 mm。考虑液体相的湍动能,则入口湍流强度可表示为
式中:u′为湍流脉动速度,m/s;uavg为平均速度,m/s;ReDH为根据流体水力直径DH计算得到的雷诺数。
由于喷嘴入口为圆,所以流体力直径DH即为圆的直径。
b.出口边界条件。出口为压力出口,大小为1个标准大气压,压力p=101325 Pa。
c.壁面边界条件。喷嘴壁面上液相满足无滑移条件,喷嘴上颗粒相满足滑移条件,计算域近壁区采用壁面函数处理,壁面处u、k、ε为零,不考虑内壁的摩擦[6-7]。
3)物料属性的设定。
液相:密度为998.2 kg/m3,动力黏度为0.001 003 kg/s[8]。
固相:固相选用石榴石,颗粒直径为0.3 mm,密度为3.50 g/mm3,动力黏度为8×10-4kg/s。
2.1.2 物理模型的建立
图5给出的是锥直型喷嘴的二维模型及网格划分,喷嘴具体的特征尺寸如图6所示。

图5 锥直型喷嘴二维模型
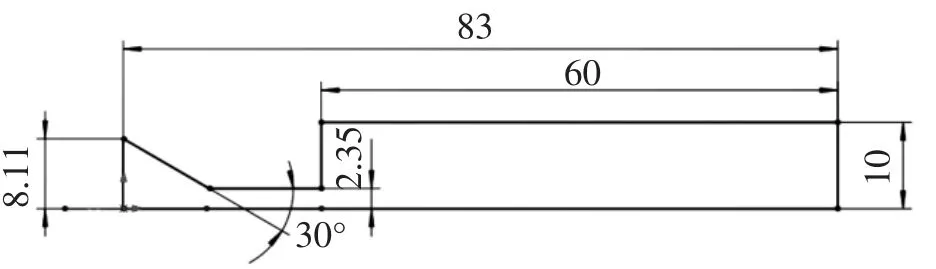
图6 锥直型喷嘴结构尺寸
喷嘴后方长60 mm、宽10 mm为喷嘴出口后的流体区域,模拟砂粒出喷嘴后在流体中运动状态[9-10](如图7)。

图7 锥直型喷嘴内外流场流体速度分布云图
2.1.3 求解结果
从图8可以看出,流体的最大速度出现在距出口12 mm处,为188 m/s;砂粒的最大速度出现在喷嘴外7 mm处,为161 m/s。
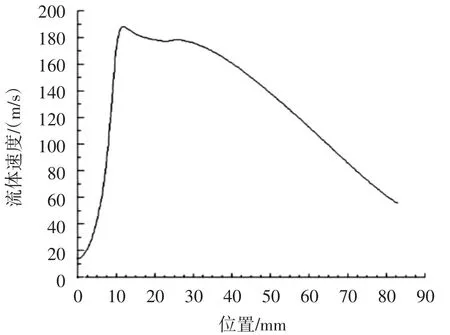
图8 锥直型喷嘴中心线位置与流体速度曲线
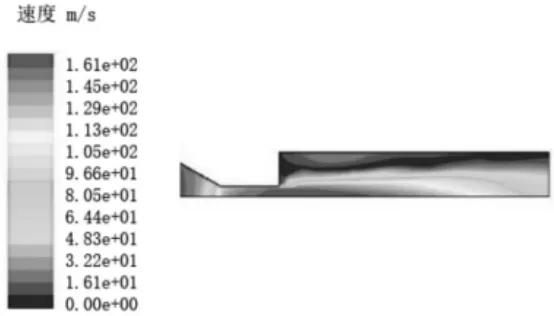
图9 锥直型喷嘴内外砂粒速度分布云图
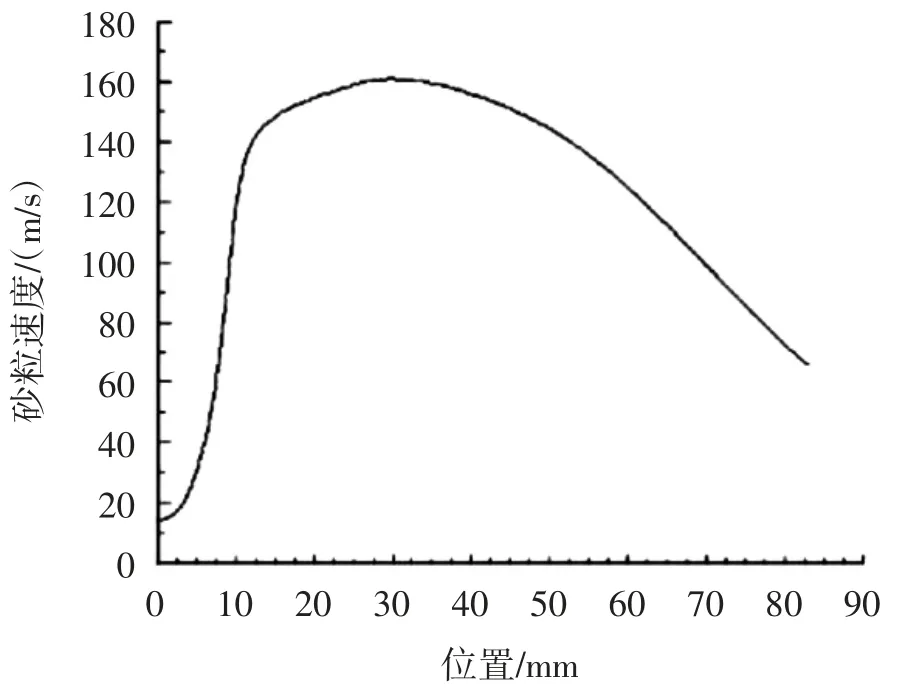
图10 锥直型喷嘴中心线位置与砂粒速度曲线
同样完成圆弧型喷嘴和抛物线型喷嘴后,整理数据如表1所示。
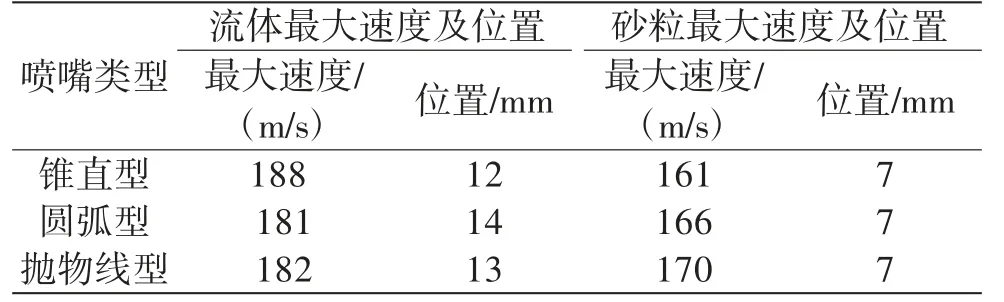
表1 喷嘴流体及砂粒速度
2.1.4 小结
1)由以上分析可知,流体和砂粒在喷嘴内外的速度分布规律基本相同,流体或砂粒经过喷嘴收缩段时进行急剧加速,经过圆柱段时速度相对稳定,而到达喷嘴外部后,由于与环境介质进行碰撞,发生能量交换,速度逐渐衰减,并出现向轴线衰减的趋势。
2)流体和砂粒经过喷嘴收缩段时同时被加速,但流体速度始终大于砂粒速度,进入喷嘴圆柱段后,流体带动砂粒持续加速,两者速度不断接近。达到喷嘴出口后,由于与周围环境发生了强烈的热量和质量交换,会形成一个核心区,此时砂粒还会加速一段距离,达到最大速度之后,速度会逐渐变小,由于砂粒密度高、质量大,速度衰减相对较慢。
3)抛物线形喷嘴砂粒出口速度最大,有利于砂粒射流切割。
2.2 喷嘴耐冲蚀性分析
2.2.1 物理模型
3种形状喷嘴的三维模型通过对二维内流场的旋转得到,如图11、图12所示。

图11 圆弧型喷嘴流场三维模型
图12 抛物线型喷嘴流场三维模型
2.2.2 求解器设置
1)边界条件。
采用离散相模型进行冲蚀分析,颗粒砂比为8%,喷嘴入口流量为197 L/min。根据流量计算可得管道内的颗粒的粒子质量流量为0.38 kg/s,颗粒由入口处均匀地射入喷嘴内。出口相对压强为0 Pa。
2)模型设定。
计算为稳态,计算域类型为流体域,即液相与颗粒相混合模型。流体域为液态的流体,流体属性为连续流体。砂粒密度为3500 kg/m3,颗粒直径为0.3 mm,参考压力为0.101 MPa。
3)求解设定[11]。
求解采用DPM模型,其中对流项的离散格式采用高阶离散格式,湍流方程的离散格式采用一阶迎风格式。收敛平均残差目标为1.0×10-4。
2.2.3 求解结果
由图13、图14可知:1)由于锥直型喷嘴入口与圆柱加速段连接处不平滑,冲蚀集中发生在该位置,且冲蚀情况比另两种喷嘴严重很多;2)圆弧型和抛物线型喷嘴入口曲线过渡非常平滑,冲蚀多发生在入口曲线的外部;3)抛物线型喷嘴的冲蚀率最低,砂粒射流中使用的时间最长。

图13 锥直型喷嘴冲蚀云图

图14 圆弧形喷嘴冲蚀云图
2.3 喷嘴结构优选
根据对不同喷嘴的分析,得到不同喷嘴的性能数据,如表2所示。

表2 不同喷嘴的性能
由表2可知:1)锥直型喷嘴虽然流体的速度最大,但砂粒加速不完全、出口速度最小,且冲蚀最严重;2)圆弧型与抛物线型砂粒最大速度相当,但抛物线型喷嘴的冲蚀率更小;3)喷嘴结构应采用抛物线型。
3 喷嘴切割套管试验
3.1 试验目的
检验所选用抛物线型喷嘴的射流切割性能及耐冲蚀性。对射流切割喷嘴的现场切割要求为:必须保证在射穿套管及地层的同时具有良好的耐冲蚀性,即在砂粒射流冲击下能保证长时间孔径不扩大。
3.2 试验设备
喷枪1支,喷嘴1支,打砂泵1台,混砂罐1个,加流体罐1个,控制台1套,试验箱1个,试验工装1套,如图15~图17所示[12]。

图15 喷枪

图16 喷嘴

图17 试验装置
3.3 试验步骤
1)检查流体罐流体量是否充足、设备是否正常;2)准备200 kg石英石(80~100目),放到加砂罐旁;3)连接管线与喷枪,将5-1/2 in套管及管线固定在流体槽内(如图17);4)检查管线,确认一切正常后起泵;5)缓慢增加泵速至泵压为5 MPa;6)按照8%砂比往混砂罐中加砂,观察设备及磨料出口是否正常;7)将泵压升至8 MPa,根据排量调整加砂量,确保砂比不变;8)时刻观察被切套管,记录套管切透时间;9)套管切割穿孔后停止加砂,继续运行1 min后停泵;10)拆卸试验工装,将喷枪及套管取出;11)测量相关数据并做记录。
3.4 试验结果
整理套管冲蚀试验数据,如表3所示。
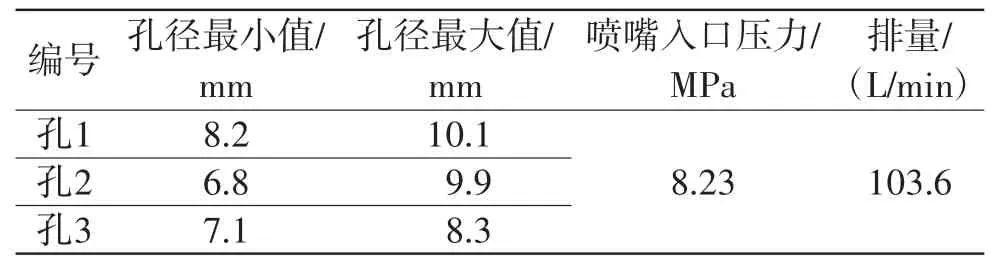
表3 射孔尺寸数据
通过表3可以看出,3个套管射孔的孔径最小值为6.8 mm,孔径最大值为10.1 mm,平均最小孔径为7.4 mm,平均最大孔径为9.4 mm。最终射孔形态接近完整圆形,满足现场使用要求。
由图18可知,喷嘴初始直径为4.42 mm;由图19可知,试验结束后喷嘴直径为4.42 mm。说明经过砂粒冲蚀后喷嘴的直径没有变化,喷嘴具有良好的耐冲蚀性。

图18 测量喷嘴初始直径

图19 测量射孔后喷嘴直径
同时,由图19可以看出,喷嘴附近喷枪表面受流体反溅严重,出现明显冲蚀凹坑,需要对喷枪表面进行硬化或者喷涂耐磨涂层处理。
4 结论
1)水力喷砂射孔选用抛物线型喷嘴,该类型喷嘴具有良好的砂粒加速性能和耐冲蚀性;
2)经过试验,该喷嘴满足水力喷砂射孔作业需求;
3)试验过程中喷枪本体反溅冲蚀现象严重,需要对喷枪进行表面耐磨处理。
