一种基于稳定性图的车铣复合机床切削稳定性研究及优化
2024-04-22曾梦玮肖夏宋冬梅刘雪垠
曾梦玮,肖夏,宋冬梅,刘雪垠
(四川省机械研究设计院(集团)有限公司,成都 610063)
0 引言
随着微型零件在航空航天、国防工业、医疗设备、核工业等领域的广泛应用,对零件的加工质量要求也越来越高。车铣复合加工技术以其速度快、精度高、复合性强等特点,在微零件制造中得到了广泛的应用。困扰于车铣组合加工中的一个严重问题就是颤振。
颤振是机床切削过程中切削刀具与工件之间产生的一种强烈相对振动现象。切削过程中出现的颤振影响了工件的加工精度和表面粗糙度,限制了切削效率,同时也会对刀具构成损坏,降低了机床的使用寿命。目前,针对切削过程中的抖振现象已有了广泛的研究[1],如Altitans等[2]提出的一种颤振稳定域分析方法,可以获得更精确的稳定域曲线;为了简化稳定域曲线的计算,李忠群[3]提出了一种构建颤振稳定域曲线的简单方法;刘冰冰等[4]构建了临界轴向切削深度和主轴速度之间的车铣稳定性图。
智能化微型零件车铣机床具有X1、Y1、X2、Y2、Z1、Z4、X4共7个直线轴,是一种多轴多刀高效加工机床。在上述研究中,稳定性图很少应用于多轴车铣复合加工中心。本文对基于稳定性图的高效车铣机床的切削稳定性进行了研究,研究结果为提高微型结构件的加工精度和表面质量提供了理论支撑。
1 构建动态数学模型
智能化微车铣机床的总体结构可分为3部分:车削主轴部分、回转主轴部分和中间刀具部分。机床利用主轴S1和后主轴S2的交替运动,通过刀具进给实现车铣组合加工功能。具体机床结构如图1(a)所示。由于机床的3个部分是独立的,因此机床可分为两个独立的加工环,包括车削主轴加工环和回转主轴加工环。刀具与加工零件之间为相对运动,工具和工件系统都可以被认为是弹簧阻尼系统,通过在三维空间坐标上建立工件和刀具的弹簧阻尼系统,可以将车铣机床的模型简化为质量弹簧阻尼(MSD)多自由度振动系统。图1(b)显示了由弹簧阻尼系统建立的车削主轴加工链和车削主轴加工链条,整个系统是一个多自由度振动系统。

图1 智能化车铣机床结构图
车削加工是一种刀具与工件正交布置的结构,它构成了刀具与工件的三维质量弹簧阻尼系统(MSD)[5]。为了构建合理的数值动力学模型,在所有方向上使用平均铣削力,刀具的振动模型可以表示为:
式中:mx、cx、kx、my、cy、ky、mz、cz和kz分别表示机床在X、Y和Z方向上的模态质量、模态阻尼和模态刚度;εx、εy、εz分别表示刀具在X、Y和Z方向上的位移分量;FTx、FTy和FTz分别表示X、Y和Z方向上的铣削分量。
对式(1)进行拉普拉斯变换,获得拉普拉斯域的车铣动力学模型,因此机床的刀具与工件系统的传递函数为
传递函数方程(2)是获得系统传递函数的基础,并为锤击试验方法获得系统传递功能提供了理论基础。
2 构建颤振数学模型
建立基于动态切片厚度的颤振数学模型是研究切削稳定性、切削参数选择和优化的基础[6]。以正交轨迹车铣过程中第i齿的切削轨迹为研究对象,车铣的车削区域如图2阴影区域所示。其中φi是第i号齿的切削角,φs是切入角,φe是切出角,b(φi)是切削角为φi时的切削宽度。切削过程中作用在齿i上的切削力为Fi,Fit和Fir分别为切向切削力分量和径向切削力分量。
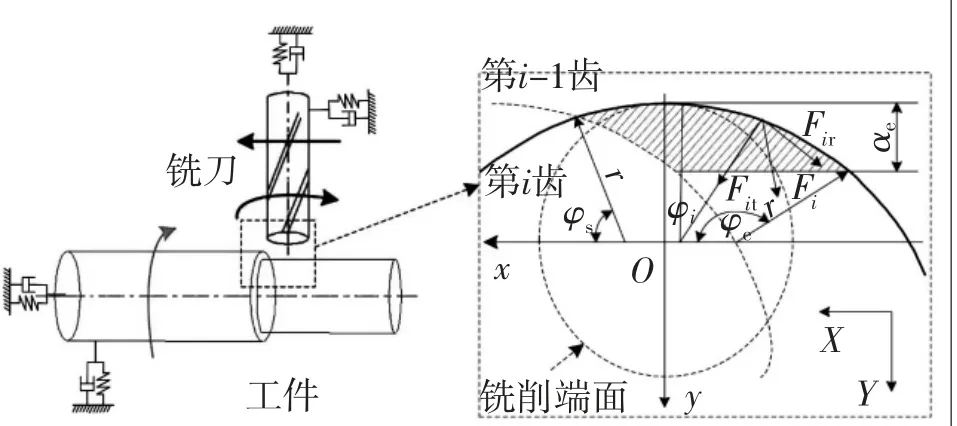
图2 车铣复合加工模型
结合图2的车铣加工模型,构建了第i齿的切削力Fi沿x轴投影的分力Fix。
根据再生颤振理论,当在t时刻对刀具施加位移指令时,会形成相应的切削厚度,称为静态切削厚度;受切削力F的影响,信号指令的给定位移和实际位移之间的差异称为动态切削厚度。切削力引起的齿与工件的振动会在工件上引起波纹,当下一个齿通过该波纹时,将创建新的波纹表面,因此动态切削厚度不仅跟当前齿的位移量相关,还取决于前一个齿的位移量。因此刀具的运动方程可以表示为下面的延迟微分方程:
式中:z为铣刀齿数,nt为铣刀速度。
假设xp(t)是理想条件下刀具的x方向位移,ξ(t)是扰动引起的位移,刀具的运动可以表示为x(t)=xp(t)+ξ(t)。由于理想状态可以表示为ξ(t)=0,因此可以得到振动位移ξ的延迟微分方程:
将式(3)转换为振动频率ω和黏滞阻尼比ζ的模态形式为:
3 构建稳定性图
为了避免车铣加工过程中的颤振,本文构建了一种微型零件车铣机床的稳定性图。稳定性图为切削深度和主轴速度之间的相互关系,包括稳定区和颤振区。在车削铣削系统中,由于刀具和工件的尺寸较小,刀具材料的刚度比工件材料的刚度高,这使得在工件系统上更容易发生颤振。正交车铣中的颤振现象是一种再生颤振[7],图3(a)显示了构建颤振稳定域曲线的简单方法,图3(b)是锤击实验过程的流程图。本文采用锤击试验方法,得到了刀具与工件系统的传递函数。本文采用锤击试验的方法得到了刀具与工件系统的传递函数,将传递函数的实部引入临界极限切削公式中[8],可以获得不同颤振频率下的临界切削深度值,并通过拟合曲线获得了样条速度和切削深度的稳定性图。
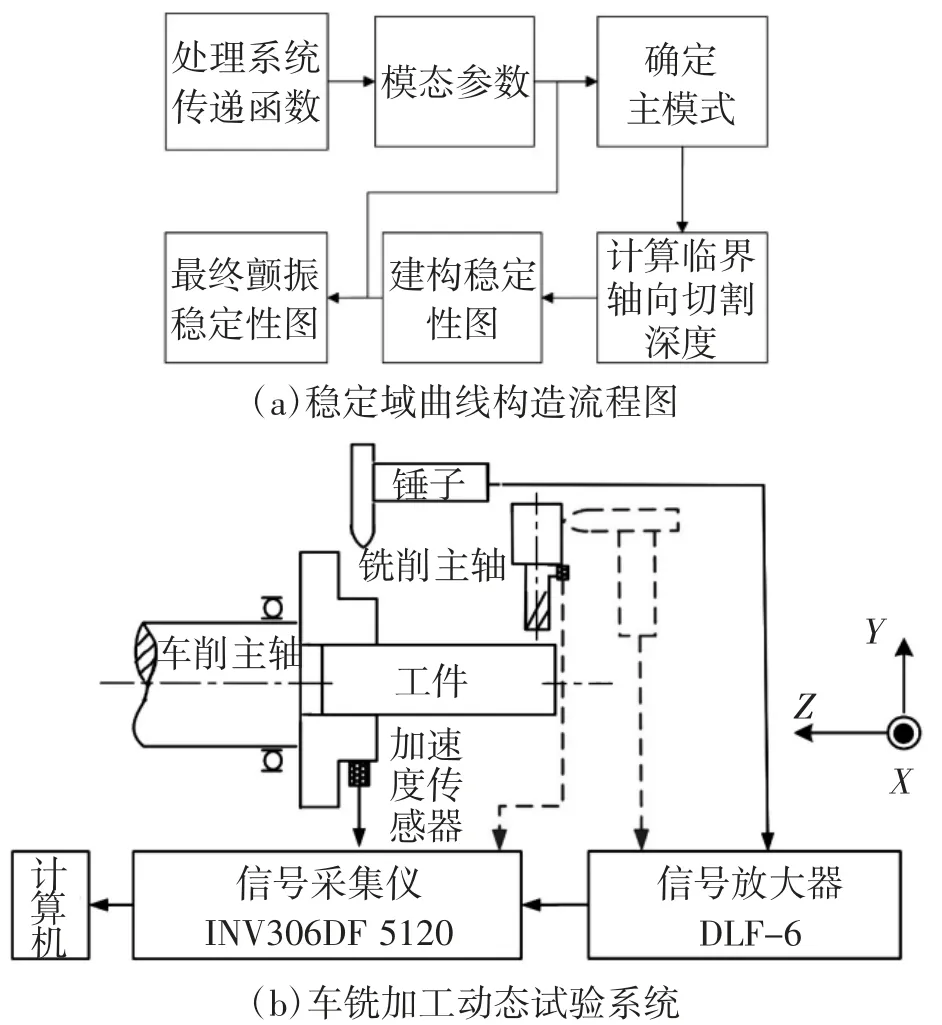
图3 稳定性图的构造流程
图4是微型零件车削和铣削稳定性的测试和测试装置,实验在一台智能化车铣机床上进行,使用一台硬质合金车刀和一台齿数z为2的ϕ2 mm硬质合金立铣刀。实验测试系统包括INV9828加速度传感器、DLF-6电压滤波集成放大器、INV3018C智能信号采集仪、计算机、YFF-1-1单向力传感器等。该实验在车削主轴、回转主轴、铣削主轴1、铣削主轴2、回转主轴1和回转主轴2上进行,以获得每个关键部件的颤振频率响应函数。

图4 锤击试验装置
根据极限轴向临界切削深度公式,对主轴模块、后主轴模块和高频铣削模块进行加工。图5为主轴车铣过程的稳定性图,包括主轴车铣平台1和主轴车铣平台2;图6为回转主轴车铣过程的稳定性图,包括回转主轴车铣平台1和回转主轴车铣平台2;图7为高频铣削过程的稳定性图。
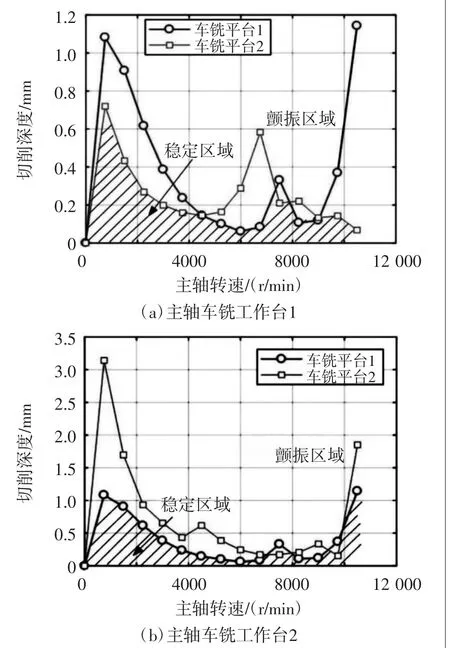
图5 主轴车铣过程稳定性图
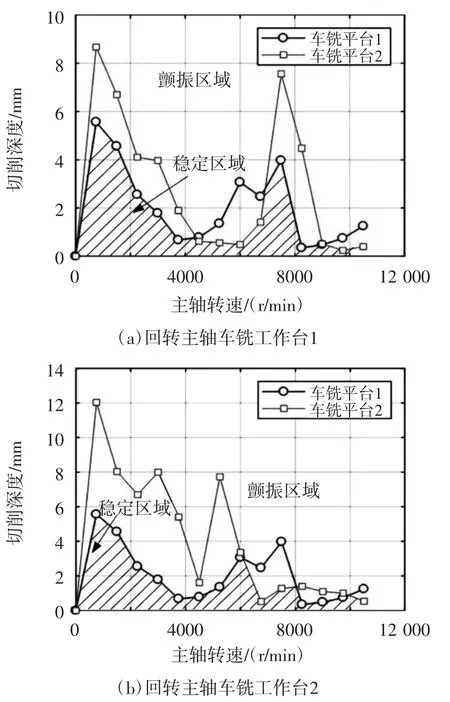
图6 回转车铣过程稳定性图
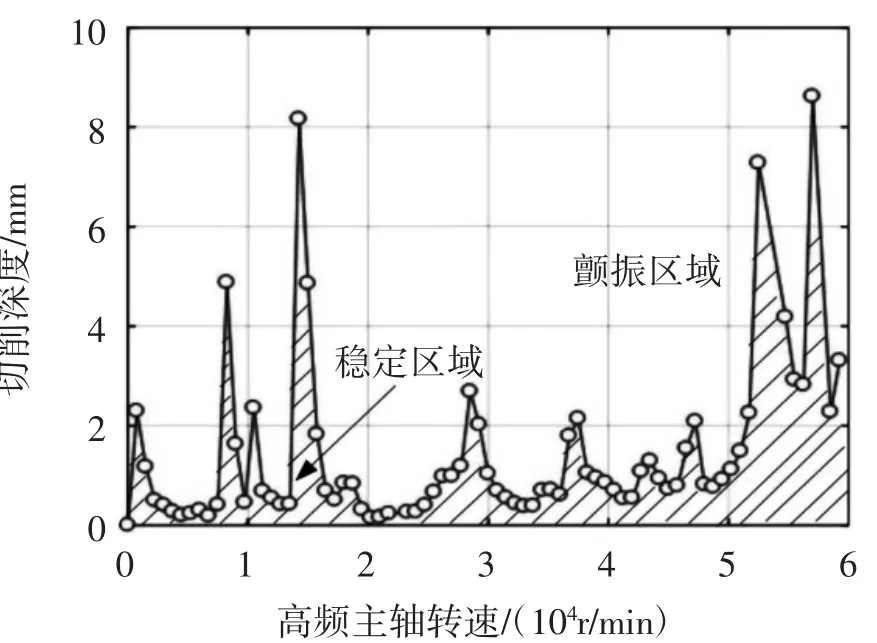
图7 高频铣削过程的稳定性图
图5(a)为主轴车铣工作台1的稳定性图,主轴车铣稳定性图由车削稳定性图和铣削稳定性图组合而成。车铣过程的稳定区域是曲线交点的下部(即阴影区域),如果加工台1选择这个稳定区域的切削参数来车削零件,就可以避免颤振的发生,同理可以选择图5(b)中稳定区的切削参数,以避免在车铣过程中发生抖振。
图6为回转主轴车铣过程的稳定性图,同理,回转车铣稳定性图由回转车削稳定性图和回转铣削稳定性图组合而成。回转主轴车铣加工的稳定区域为曲线交点的下部(即阴影区域),选择图6稳定区切削参数,可避免车铣过程中的抖振。
图7显示了高频铣削过程的稳定性图。可以看出,在稳定区切削参数的选择,可以用于切割微型零件。
4 结论
1)本文建立了一种微型零件车铣机床的动力学模型。结合机床多轴、多刀具的加工特点,构建了高效微车铣床多自由度振动动力学数学模型,为传递函数的计算提供了理论依据。
2)本文建立了一种基于切削厚度的微车铣颤振数学模型,并基于动态切削厚度,建立了微车铣削颤振数学模型,得到了颤振中的振动频率ω和黏滞阻尼比ζ,为切削稳定性图的研究提供了理论依据。
3)构建了高效微车铣机床的稳定性图。通过试验锤击法,得到了高效车铣机床各关键部件的传递函数,构建了车削主轴车铣稳定性图、回转主轴车铣稳定性图和高频铣削稳定性图,研究结果对指导和优化微零件车削加工工艺提供了理论支撑。
