一种小型激光跟踪测量系统的研制

顾超伟, 缪东晶, 严利平, 刘 洋, 李建双

(1.浙江理工大学 纳米测量技术实验室，浙江 杭州 310018；2.中国计量科学研究院，北京 100029)

1 引 言

大型工艺设备如飞机机身、船舶壳体、铁路车辆等,其生产制造的质量均需要通过大尺寸测量技术提供保证[1,2]。为了满足各类大型设备测量需求,目前已有的大尺寸坐标测量系统主要有激光跟踪测量系统、近景摄影测量系统、室内空间测量定位系统等[3]。其中激光跟踪测量系统是一种可以实现对目标进行动态跟踪与坐标测量的系统,具有精度高、量程大、速度快等优点,因此广泛应用于现代大型装备制造中[4～7]。

国外对激光跟踪测量系统的研究起步较早,技术发展相对成熟并且早已有成型的产品投入到市场中。国内从1996年沈飞集团首次引入激光跟踪仪开始[8],逐步开展了激光跟踪仪的研究。1999年清华大学刘永东等设计了三站激光跟踪坐标测量系统,实现了平面运动目标坐标的跟踪测量[9];2003年天津大学李杏华等设计了基于多边法的四路激光跟踪干涉柔性测量系统[10],开展了跟踪测试实验,跟踪速度为0.4 m/s;2007年四川大学谢驰等设计的激光跟踪仪[11],利用同轴光路双频干涉测量尾数计算距离,采用CCD器件作为光斑位置反馈单元,该系统实现了20 m范围内测长精度为±(40+1.5×10-6L)μm;2012年天津大学张亚娟设计了一种单站式跟踪仪,该系统可实现在3.2 m的范围内对目标以0.5 m/s的速度进行跟踪[12];2015年哈尔滨工业大张逸飞、吴婷等设计了基于双频干涉量的跟踪仪[13,14],跟踪距离范围0.3～10 m,最大跟踪速度0.9 m/s;2016年中国科学院董登峰、周维虎等设计了基于干涉测距的激光跟踪仪[15],该系统跟踪测距范围可达41.7 m,跟踪速度可达2 m/s;2020年北京工业大学宋辉旭提出了一种以固定标准球为反射装置的二维回转轴系结构,分析了二维回转轴系回转误差,有效抑制了轴系回转误差对系统测距精度的影响[16];2021年哈尔滨工业大学王红智设计了一种基于相位式测距的跟踪仪[17],该系统在11 m的跟踪范围内跟踪角速度可达126.81°/s;2021年中图仪器股份有限公司上市的GTS激光跟踪仪,在大尺度空间测量工业科学仪器中具有高精度和重要性,同时具有μm级别精度。因此,国内虽然对激光跟踪测量系统的研究起步相对较晚,但近几年也逐步有产品投入到市场中。通过对当前市场上的激光跟踪测量系统的结构与功能分析,可以发现当前激光跟踪测量系统正越来越往小型化、高集成、便携式的方向发展。

为了设计一种体积更小、重量更轻、便携性良好的激光跟踪测量系统,本文首先从激光跟踪测量系统理论基础入手,分析了系统整体工作原理与跟踪控制关键参数,设计了系统的机械结构、光学模块以及跟踪控制模块,开发了三维可视化测量软件,最后通过实验测试验证系统跟踪稳定性、位移分辨力、跟踪速度、跟踪距离测量范围以及三维测量软件功能。

2 激光跟踪测量系统理论分析

2.1 激光跟踪测量系统工作原理

激光跟踪测量系统通过驱动水平和俯仰电机来实现对目标的跟踪,通过角度编码器与测距仪实现对目标偏摆角度与跟踪距离的测量,通过上位机对偏摆角度与跟踪距离进行解算来得到目标的三维坐标。图1所示为激光跟踪测量系统的工作原理图,其中PSD(position sensitive detector)为位置敏感探测器,BS为分光镜,MH、MV分别为水平和俯仰步进电机,DH、DV分别为水平与俯仰步进电机的驱动器。

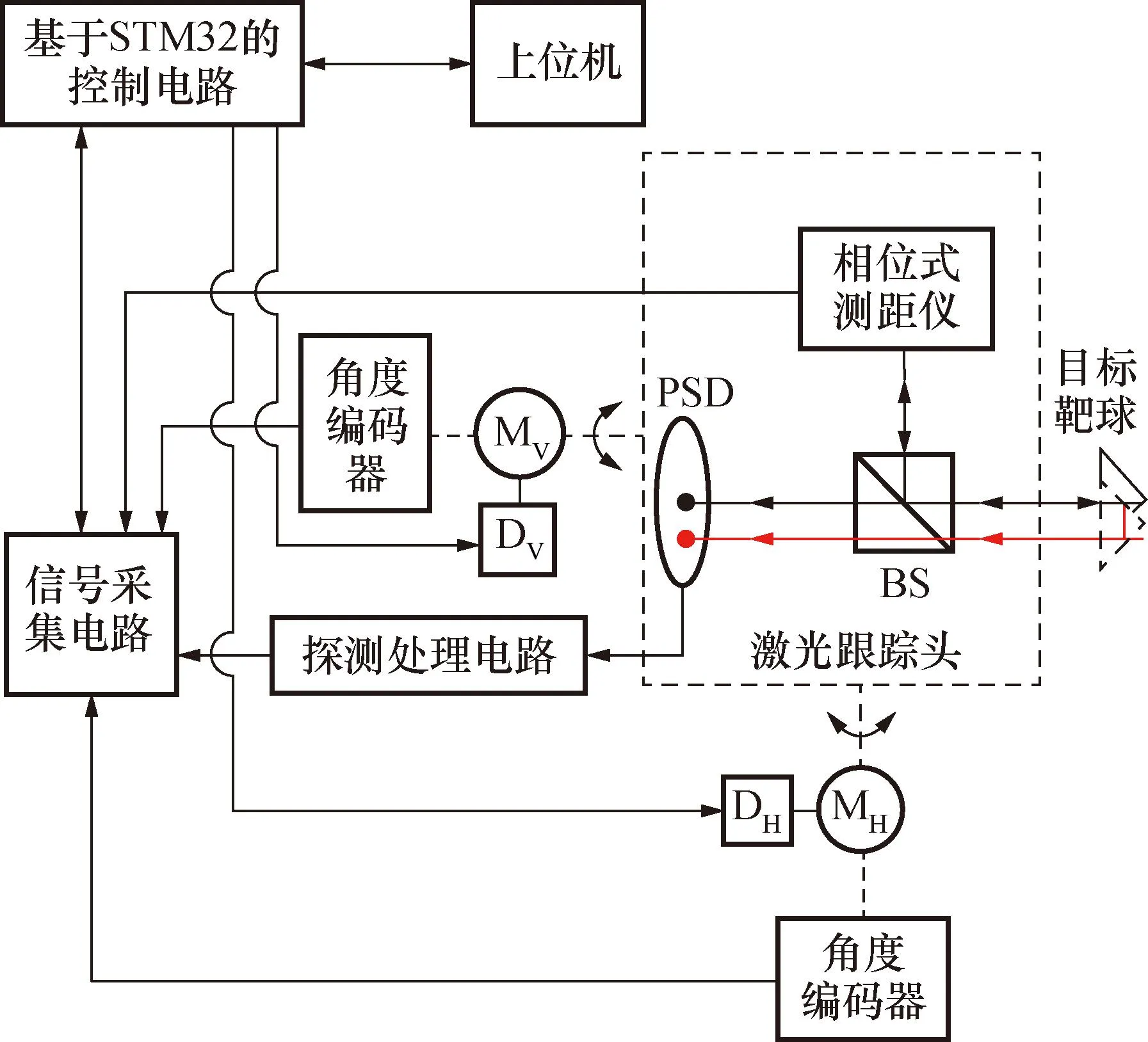
图1 激光跟踪测量系统工作原理图Fig.1 Principle of laser tracking measurement system

首先,相位式测距仪中发出的光束经BS反射到目标靶球,经目标靶球反射后的光束平行于原光束返回到BS上,BS将返回的光束分成2束,其中1束反射回至相位式测距仪进行跟踪目标靶球距离的测量,另外1束透射BS后入射至PSD表面,进行激光偏离目标靶球中心位置量的精密探测,探测信号处理电路将PSD探测到的电流信号先进行电流信号至电压信号的转换,然后再进行信号放大处理。信号采集电路同步采集PSD位置偏移电压、测距值以及水平和俯仰角度值,然后传输至基于STM32的控制电路。控制电路进行数据处理与脉冲信号的生成,并将生成的脉冲信号传输至驱动器,随后驱动器驱动二维电机旋转,进而使PSD位置偏移量趋近于0,完成对目标靶球的跟踪控制。最后,上位机根据接收的偏摆角度值与测距值来进行目标三维坐标值的解算。

系统的三维空间坐标的测量方式为球坐标测量,其基本原理主要为:由相位式测距仪测得目标至系统的距离L,由角度编码器测出跟踪目标的水平角θ和俯仰角φ,再通过球坐标与直角坐标转换关系式(1)获得目标的空间直角坐标(x,y,z)。

(1)

2.2 系统跟踪控制关键参数分析

为提高系统的跟踪控制性能,必须对系统在跟踪过程中的所有关键参数进行数学分析。图2所示为系统在水平方向跟踪时的参数分析模型,P1位置处激光正好位于靶球中心位置,目标靶球移动dT(dT小于系统脱靶距离)到达了下一个位置P2,此时PSD位移探测值为dP。跟踪控制模块每隔周期T采集1次dP的值,因此为了提高跟踪速率要求系统在时间T之内完成当前dP重新为0的跟踪工作。上述过程中,dT、靶球偏摆角θ、系统至靶球的距离L之间的关系为:

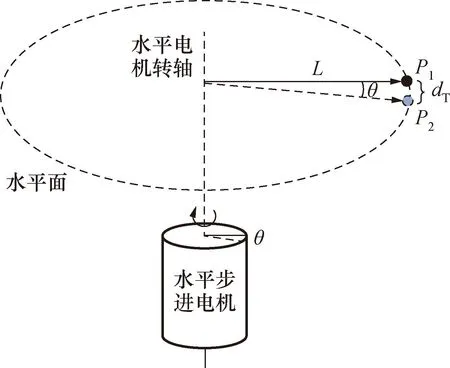
图2 参数分析模型Fig.2 Parameter analysis model

dT=θ·L

(2)

步进电机步距角与步进脉冲频率分别为Δθ、fh,假设系统在PSD信号采集周期T内刚好完成跟踪,则在这一过程中步进电机一共会收到的脉冲数M为:

(3)

由于θ=M·Δθ,因此结合式(2), 式(3)可以得出步进电机的驱动频率fh为:

(4)

在本系统中dP与dT存在着固定的数学比例关系

dP=k·dT

(5)

式中k为偏差比例系数。因此此时驱动频率可以表示为:

(6)

跟踪速度vh为:

(7)

跟踪加速度ah为:

(8)

上述vh、ah均为系统在理想状态下的速度、加速度值;在实际的跟踪过程中,由于受到电机延时与机械阻力等因素的影响,系统无法按实现理想情况下进行跟踪控制。因此,为了提高系统的跟踪控制性能,在控制系统中引入了PID控制,其数学表达式为:

(9)

式中:dPID为经过PID控制后的PSD的输出量;kp称为比例增益;ki为积分常数;kd为微分常数;Δe(k)=e(k)-e(k-1)为微分项,e(k)为输入偏差。经实验测试发现,相比于未加入PID控制时的跟踪情况,加入PID控制后的系统的跟踪性能会有显著的提高。

3 系统各部分设计与实现

3.1 机械结构设计与实现

图3所示为系统结构图,系统在机械设计上采用了光机电一体化的集成设计方式,这种设计方式将光学模块、机械结构、电路控制模块集成一体,实现了系统的结构紧凑性和内部系统与外界环境的独立性,不仅可以减小系统体积、提高便携性,还可以减小外界因素对系统内部的干扰。

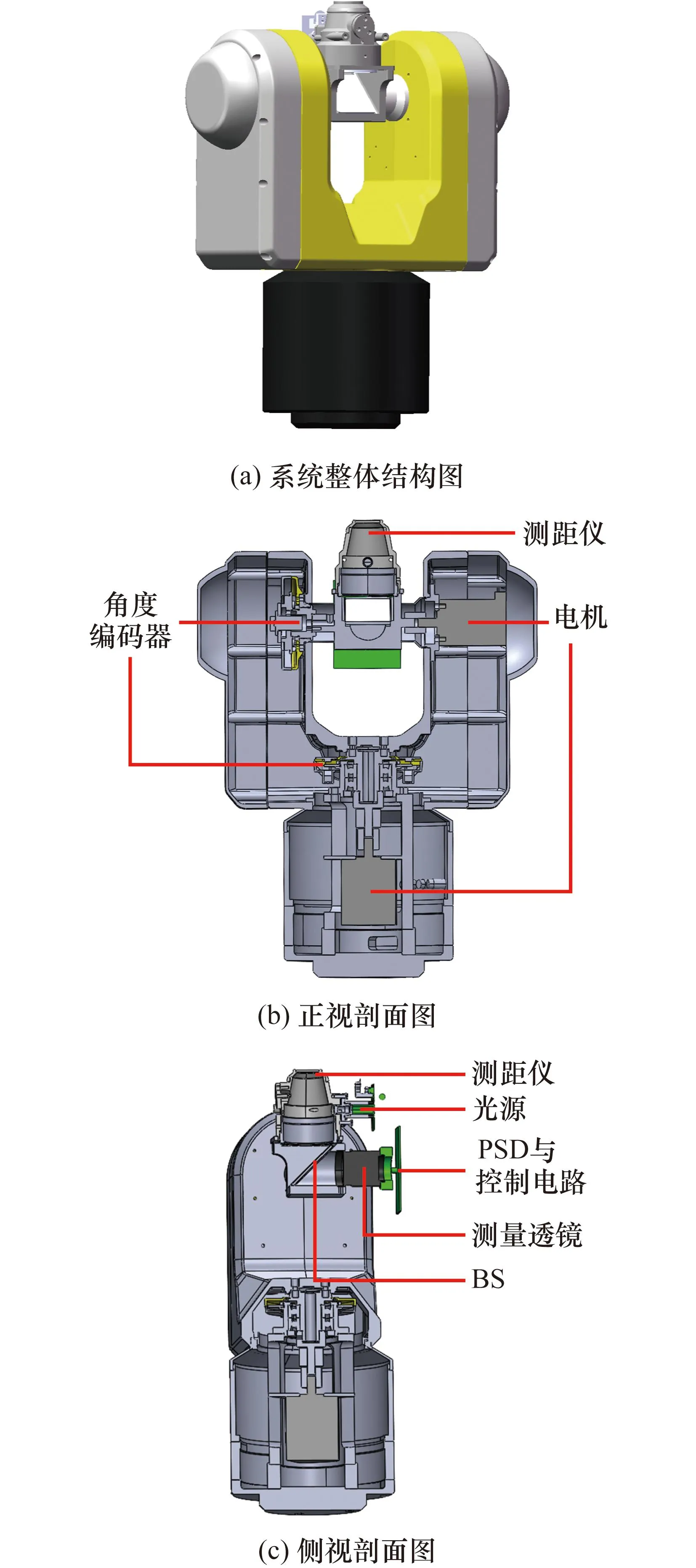
图3 光机电一体化结构图Fig.3 Opto-mechatronics structure diagram

图3(b)为激光跟踪测量系统的正视剖面图。测距仪置于跟踪头的顶端,测量光从此处射出并参与目标的跟踪与测量。角度编码器分别与水平和俯仰旋转轴系同轴连接,实现对系统的水平和俯仰方向偏摆角度的测量。为了实现系统的快速跟踪和保证跟踪控制精度,水平与俯仰轴系分别同轴连接了一个电机,并由各自的驱动器进行驱动运转。

图3(c)为激光跟踪测量系统的侧视剖面图,由图可知,在跟踪头的机械结构设计上,本系统将光学模块以及电路控制模块等整体集装起来置于空间二维旋转跟踪头上。该方式首先减少了光学器件的使用,减小了光路中测量光能量的损耗,降低了系统制造成本;其次该方式使得跟踪头在俯仰方向转动的角度更大,可以增大系统的俯仰方向测角范围;最后,该方式使内部光路与外界环境产生了隔离,有效减小了外部环境因素的干扰。

图4为系统的样机图。表1为该样机的体积与重量及系统的测角范围测试结果,由表1可知,与国内现有集成度与测角范围最高的其他商用跟踪仪相比,该系统在体积上、重量上、角度测量范围上均具有一定优势。

表1 参数测试结果与对比Tab.1 Parameter test results and comparison

3.2 光学模块设计与分析

光学模块主要功能为实现跟踪目标的距离测量以及跟踪目标偏差量的采集。图5所示为激光跟踪测量系统的跟踪测量光路图,其中P1、P2分别为目标靶球的初始位置与移动后的位置,dT为P1与P2之间的距离、d为返回光束的偏移距离,dP为PSD表面光斑偏移距离。光路工作原理为:

图5 跟踪测量光路图Fig.5 Tracking and measuring optical path diagram

目标靶球的位置偏差量在光路中被转换为PSD表面光斑的位置偏移量,PSD通过将光斑能量转换为4个电极的电流输出来探测光斑位置偏移量。由于电流信号微弱不易被采集,因此需要通过探测信号处理电路进行电流至电压信号的转换以及电压信号的放大处理。

PSD是整个光学模块中尺寸最小的光学器件,其尺寸的大小决定了跟踪过程中目标靶球允许的最大偏差量。如果将目标靶球反射回来的光直接入射到PSD表面,那么系统进行远距离的跟踪测量时,入射到PSD表面的光斑尺寸与PSD的尺寸将十分相近,目标靶球的最大偏差量将会大幅减小,严重影响系统的跟踪控制性能。

为增大跟踪过程中目标靶球允许的最大偏差量,在图5光路中的PSD前方增加了一个测量透镜。从目标靶球反射回来的激光光束在经过测量透镜后进行汇聚,PSD表面的光斑尺寸也随之变小,目标靶球允许的最大偏差量也因此得到大幅提高。

图5中,d与dT之间的关系为:

d=2dT

(10)

靶球的偏移距离dT与PSD表面光斑位置偏移值dP具有的数学关系:

dP=k0·d

(11)

式中:k0为比例常数,由测量透镜的焦距以及测量透镜摆放PSD的距离决定。结合式(5)、式(10)、式(11)可知,

dP=k·dT=2k0·dT

(12)

为测试PSD位置偏移量与目标偏差量之间的偏差比例系数k、目标靶球允许的最大偏差量、PSD线性区间范围,本文进行了系统的PSD标定实验,如图6所示。通过水平位移台来移动目标靶球,使测量激光在靶球中心位置[-6 mm,6 mm]范围内以1 mm为步长进行步进运动,目标靶球距离控制在系统常规作业距离5 m的范围之内。记录上述运动过程中的PSD位置偏移值,并对PSD的位置偏移值进行重复性分析,然后将PSD的位置偏移信息绘成曲线,得出线性区间,最后再将线性区间进行直线拟合,得到目标靶球允许的最大偏差量、最大线性误差以及偏差比例系数k。

图6 PSD标定实验Fig.6 PSD calibration experiment

水平方向的PSD标定实验数据分析曲线如图7所示。图7(a)为标定过程中的数据曲线,dPx1、dPx2和dPy1、dPy2分别代表2次重复标定过程中PSD水平与俯仰方向的偏移值,标定过程中俯仰方向的PSD偏移值趋于0且基本不变,说明系统摆放平面与目标运动平面基本平行。

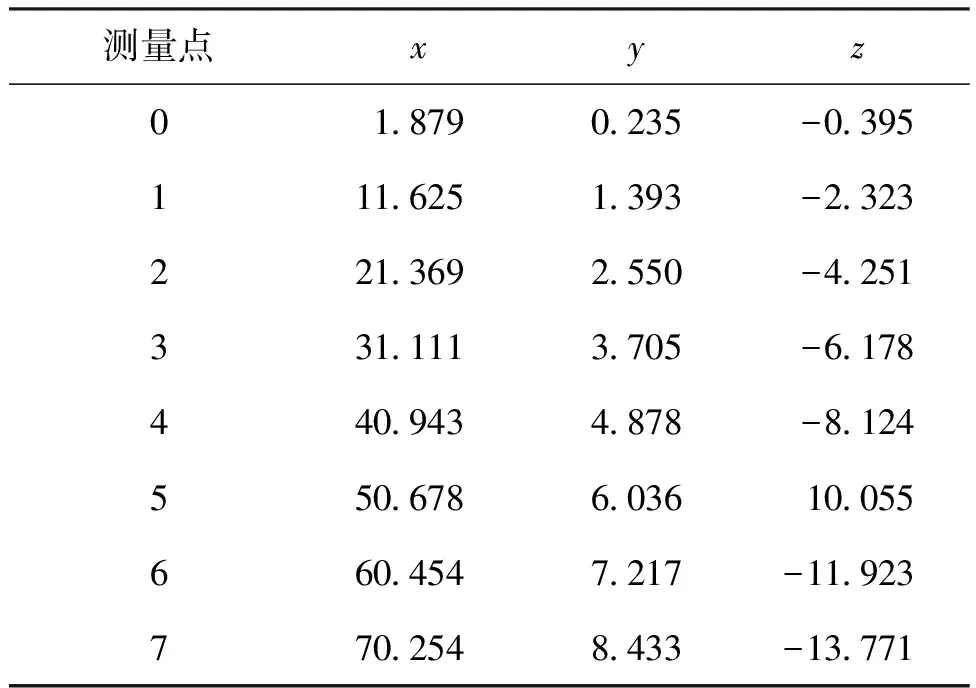
表2 跟踪距离范围测试Tab.2 Tracking range test m

图7 水平方向PSD标定实验数据分析Fig.7 Analysis of horizontal PSD calibration experiment data

为验证实验数据的重复性,对图7(a)中的数据进行了重复性分析,实验结果如图7(b)所示,图中sPx、sPy分别为水平与俯仰方向的PSD重复性标准差值,实验结果显示系统重复性误差为3.5 μm,系统具有较好的重复性。

从图7(a)中可以发现,当激光在目标靶球中心位置附近±3 mm区间内运动时,PSD的光斑偏移值变化范围为(-800 μm,800 μm),具有明显的线性。将这段区间内的数据单独进行直线拟合分析,结果如图7(c)所示,其中dPx、dFx分别代表PSD水平方向的偏移量及其直线拟合值。实验结果显示,偏差比例系数k=274,说明在PSD水平方向线性区间内目标靶球每移动1 mm,PSD偏移量则将会变化 274 μm,线性区间内的非线性误差不超过40 μm;经测试,相比于未加测量透镜,目标靶球允许的最大偏差量增大了3倍。PSD俯仰方向结果与水平方向一致,在此处不再详细赘述。

3.3 跟踪控制模块设计与分析

跟踪控制模块主要负责PSD位置偏移信号与测距信号的采集,然后根据这些信号来生成电机驱动信号,从而来控制电机运转进而实现对目标的跟踪。图8所示为激光跟踪测量系统的跟踪控制模块原理框图。首先信号采集电路采集PSD水平和俯仰方向的位置偏移电压dPx、dPy与目标距离L,随后STM32的控制电路基于这些数据进行频率分别为fh、fv的脉冲生成,驱动器接收脉冲信号后驱动水平和俯仰电机进行二维旋转,实现对目标的跟踪。

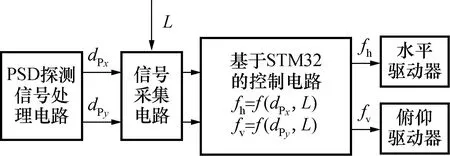
图8 控制模块原理框图Fig.8 Control system block diagram

基于STM32的控制电路是跟踪控制模块的核心部分,其跟踪控制算法的设计是系统能否实现高效快速跟踪的关键,为了实现系统的快速跟踪且保证系统的跟踪精度,设计了如图9所示的跟踪控制算法的流程图。

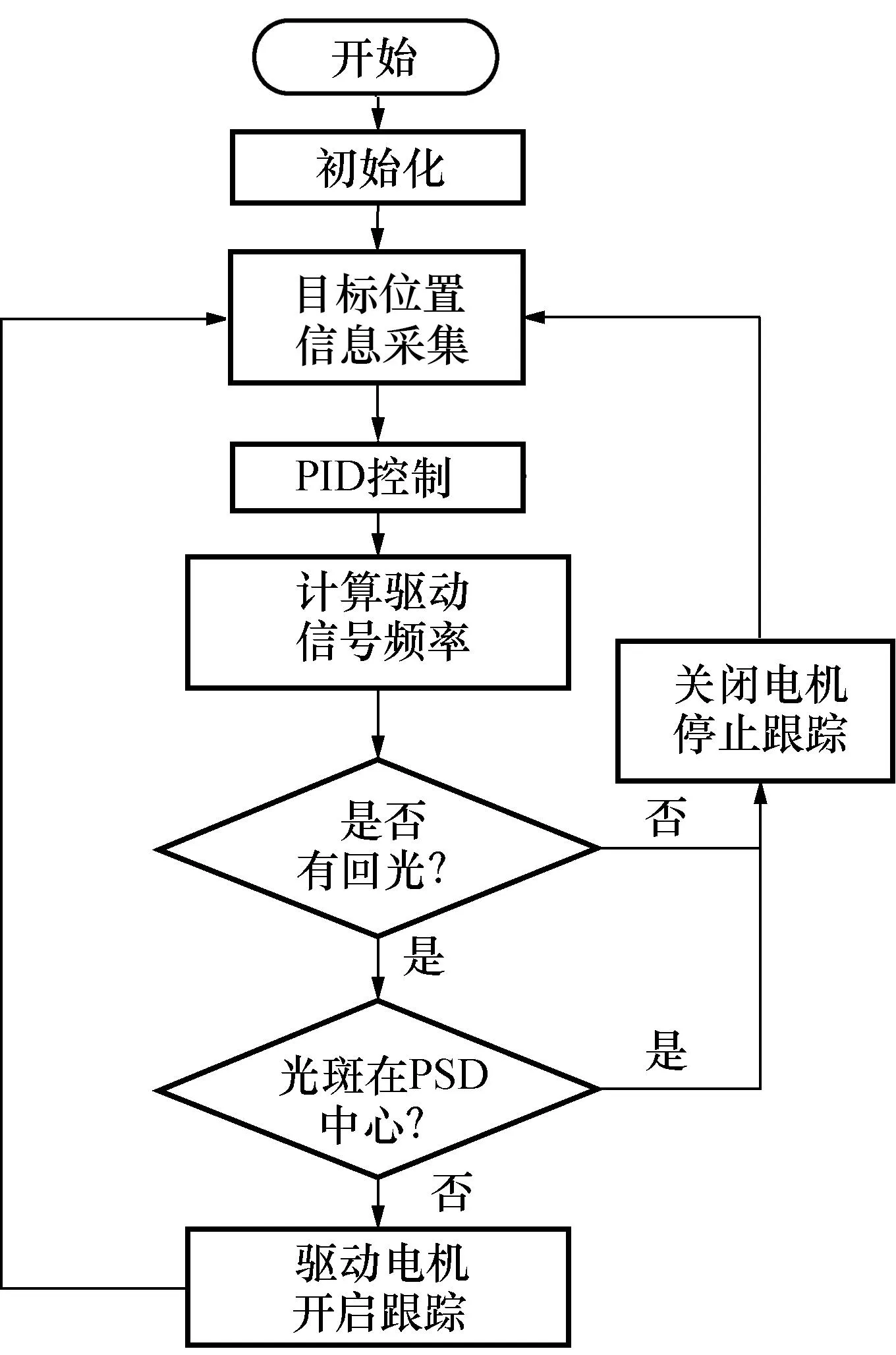
图9 跟踪控制算法流程图Fig.9 Flow chart of tracking control algorithm

算法原理主要为:在初始化阶段主要完成测距值、电机使能状态、控制时钟及频率值、PID控制参数、串口信息、AD采集功能等的初始化,为后续跟踪控制做好准备;在开始跟踪后,电路根据采集到的PSD位置偏移电压值与目标距离值进行驱动信号频率的生成,分别通过判断测量光是否有回光和光斑是否在PSD中心位置来决定是否开启电机进行跟踪;如果测量激光没有回光或者是光斑在PSD中心位置则关闭电机停止跟踪,则使系统保持在原位不动,反之则驱动电机进行运动,使PSD光斑保持在PSD的中心位置,从而来实现对目标靶球的跟踪。

3.4 三维可视化测量软件开发

三维可视化测量软件主要功能为用户端对跟踪目标的坐标测量、三维动态显示和跟踪运动仿真。系统采用面向对象编程的C Sharp(C#)程序设计语言,选用稳定性与兼容性强的.NET Framework 4.8作为基础开发框架,结合Open CASCADE Technology (OCC)三维几何建模库进行了软件的开发。图10所示为软件的功能设计图。

图10 测量软件功能结构Fig.10 Measure software functional structure

测量软件通过串口协议和下位机进行通信,通过C# 语言,基于.NET Framework 进行开发,在三维显示与建模方面,采用OCC几何建模库与C++语言实现模型与测量结果的三维动态显示与操作,并将算法封装成DLL文件;上位机通过调用各个DLL库提供的功能接口,完成三维可视化测量软件的整体开发。

4 实验验证与结果分析

4.1 跟踪稳定性测试

为评定激光跟踪测量系统的稳定性,进行了系统在静止过程中PSD位置偏移量变化范围测试。首先将测量光对准目标靶球的中心位置并保持靶球与系统的位置静止不动,目标靶球距离控制在系统常规作业距离5 m的范围之内,持续10 s;然后将10 s内PSD的偏移值记录并绘制成曲线,实验结果如图11所示。由实验结果可知,系统在静止时,PSD位置偏移量稳定在0 μm上下,PSD自身会产生20 μm左右的偏移量。

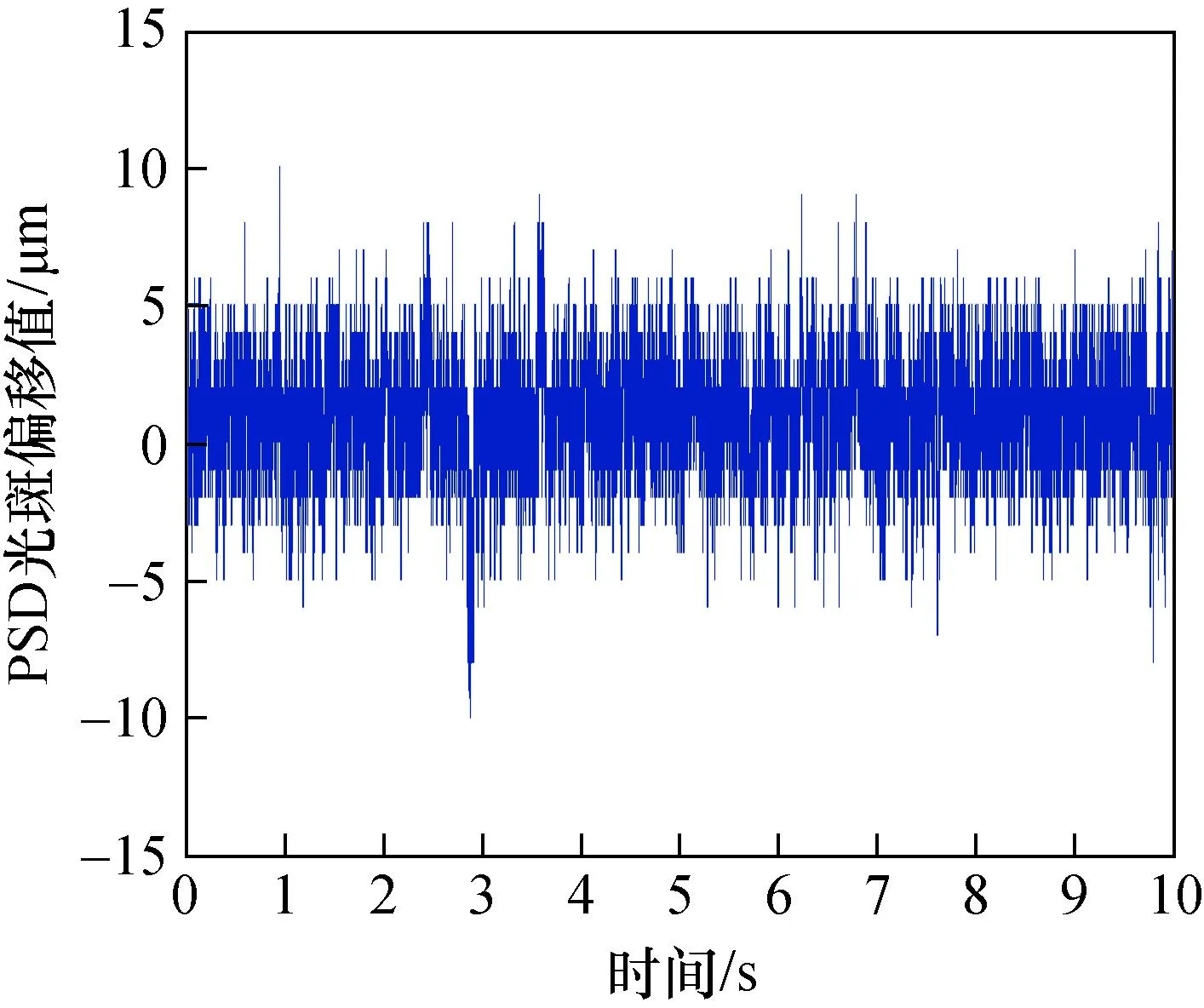
图11 系统跟踪稳定性测试Fig.11 System tracking stability test

4.2 位移分辨力测试

为测试系统的位移分辨力,利用精度不低于 1 μm 大理石气浮位移导轨进行了系统的位移分辨力测试实验。首先将激光光束固定在目标靶球中心位置,目标靶球距离仍然控制在系统常规作业距离5 m的范围之内,然后分别连续进行20 μm与40 μm的步进运动,运动时间持续10 s且步进间隔为1 s,实验结果如下图12所示。根据图像中的曲线阶梯变化是否明显来得出系统位移分辨力,由实验结果可知,在位移导轨进行40 μm的步进运动时,台阶效果明显,因此系统的位移分辨力可以达到40 μm以上。

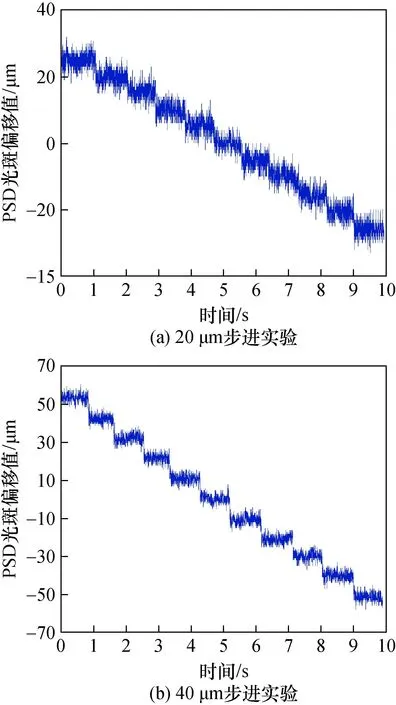
图12 位移分辨力测试实验Fig.12 Displacement resolution test experiment

4.3 跟踪测量性能测试

4.3.1 跟踪速度测试

实验主要依托ABB公司IRB2600型机械臂来带动靶球分别以不同速度、加速度、轨迹进行运动,从而来测试系统的跟踪性能各项指标。实验中所使用机械臂工作范围为1.65 m,负载能力达到20 kg,重复定位精度0.04 mm,重复路径精度达到0.13 mm。

实验场景如图13所示,使用Robotstudio软件对机械臂进行编程控制,使目标靶球分别在点A1与A2之间进行水平方向的轨迹长度为1 m的直线运动、点B1与B2之间进行俯仰方向的轨迹长度为 1 m 的直线运动、点C1与C2之间进行45°方向的轨迹长度为1.4 m的直线运动。选取的点与系统的距离为系统常规作业距离5 m,运动轨迹包含了水平轨迹、俯仰轨迹、45°方向轨迹,因此,可以全面地测量激光跟踪测量系统的跟踪性能。

图13 跟踪性能测试实验Fig.13 Track performance test experiments

图14所示为系统在进行跟踪测试时的跟踪速度曲线图,其中vx、vy、vxy分别代表水平方向、俯仰方向、45°方向的运动轨迹的跟踪速度,由于在运动中机械臂需要通过减速调整关节来保持运动姿态,因此运动速度曲线也存在轻微起伏。实验结果显示,系统在水平方向具有最高速度与加速度,分别为480 mm/s与506 mm/s。由于当前样机跟踪头重量配置不平衡,重心偏移俯仰轴,轴系也未进行垂直标定,系统在俯仰方向与45°方向的跟踪性能均小于水平方向。

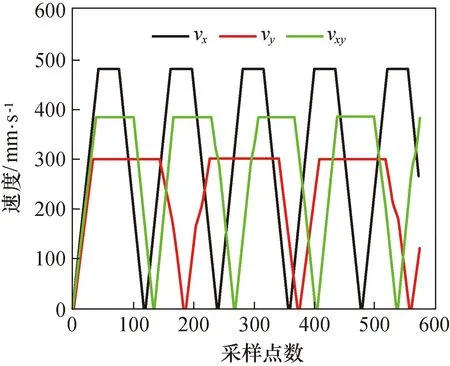
图14 跟踪速度曲线Fig.14 Tracking velocity

4.3.2 跟踪距离范围测试

为测试系统的跟踪测量范围,在中国计量科学研究院几何计量科学研究所大尺寸计量研究室的80 m室内长标准装置实验室进行了跟踪距离范围测试实验。80 m室内长标准装置具有自动控制的运行平台装置与干涉测距功能,其测量精度达到0.1 μm。

图15为系统跟踪距离测量范围测试实验现场图,将系统样机固定在80 m长导轨上的平台上,靶球固定在气浮移动平台上,为了保证靶球在移动过程中系统一直在跟踪,将系统摆放在靶球移动的直线路径的一侧。控制平台由近向远步进运动,每次步进距离约10 m,直至系统出现了断光。

图15 跟踪距离范围测试Fig.15 Tracking range test

表2所示为步进实验的坐标测量结果,由实验结果可知,当测量距离>70.152 m时出现了断光,无法进行跟踪,因此系统跟踪测量距离范围不小于70 m。

4.3.3 三维可视化测量软件功能验证

三维可视化测量软件是系统的重要组成部分,本文进行了软件的功能验证。测量软件的工作界面如图16所示,图中,数据区主要负责测量信息的显示与测量指令的发送,菜单区主要负责三维模型的动态操作与数据处理,三维显示区主要负责系统跟踪动作的三维显示。本测量软件不仅可以实现对目标角度、距离、坐标的测量与存储,还可以实现对跟踪过程进行三维动态显示。

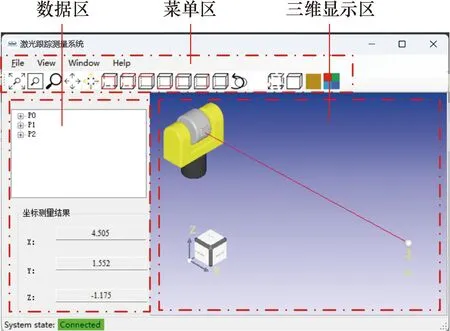
图16 三维可视化测量软件Fig.16 3D visual measurement software

5 结 论

研制出一种体积小、重量轻、便携式的小型激光跟踪测量系统。采用光机电一体化集成设计方式,实现了系统体积与质量的减小,抗干扰能力的提高以及俯仰角度测量范围的增大。通过优化基于PSD的目标偏差量采集部分光路,实现目标靶球允许最大偏差量的增大。完成了系统跟踪控制模块的设计、跟踪控制算法与三维可视化测量软件的开发。通过实验对系统的各项功能与参数进行测试,实验结果显示,系统跟踪稳定性与位移分辨力分别为 20 μm 和40 μm、跟踪速度最高可达480 mm/s、跟踪加速度最高可达506 mm/s2、跟踪距离范围不小于70 m、具有三维坐标测量与三维可视化功能。

相比现有跟踪仪,本文研制的激光跟踪测量系统在体积、重量以及测角范围方面均具有一定优势。该系统跟踪测量性能良好,可应用于大尺寸测量中运动目标的动态跟踪与动态坐标测量当中,具有良好的应用前景。后续将在测量精度、测量软件功能、轴系机械误差等方面进一步提高与改进,将应用领域扩展到航空航天、国防军事设备等其他高尖端领域。