Stress-corrosion coupled damage localization induced by secondary phases in bio-degradable Mg alloys: phase-field modeling

Cho Xie ,Shijie Bi ,Xio Liu ,Minghu Zhng ,Jinke Du

a The Faculty of Mechanical Engineering and Mechanics, Ningbo University, Ningbo 315211, P. R. China

b Key Laboratory of High Temperature Wear Resistant Materials Preparation Technology of Hunan Province, Hunan University of Science and Technology,Xiangtan 411201, P. R. China

Abstract In this study,a phase-field scheme that rigorously obeys conservation laws and irreversible thermodynamics is developed for modeling stress-corrosion coupled damage (SCCD).The coupling constitutive relationships of the deformation,phase-field damage,mass transfer,and electrostatic field are derived from the entropy inequality.The SCCD localization induced by secondary phases in Mg is numerically simulated using the implicit iterative algorithm of the self-defined finite elements.The quantitative evaluation of the SCCD of a C-ring is in good agreement with the experimental results.To capture the damage localization,a micro-galvanic corrosion domain is defined,and the buffering effect on charge migration is explored.Three cases are investigated to reveal the effect of localization on corrosion acceleration and provide guidance for the design for resistance to SCCD at the crystal scale.

Key words: Phase field;Mg alloys;Stress-corrosion coupled damage;Damage localization;Finite element method.

1.Introduction

With the increasing demand for high quality in health and medicine,intelligent health-promotion technologies have attracted extensive attention.In recent years,Mg alloys have been highly acclaimed as a new generation of biological transplantation materials,because of their significant advantages,such as their mechanical properties which are similar to those of human bone tissue [1,2],good biocompatibility[3],and degradability [4].However,its major drawbacks include a weak corrosion resistance[5]and a tradeoff[6]among its corrosion rate,strength,fatigue durability,plasticity,and physiological toxicity.Currently,the prevalently used coating technology cannot effectively protect materials during deformations,especially large deformations or cyclic deformations.Microcracks tend to appear at sharp corners and interfaces,thus becoming the starting point for local damage [6].In addition,the trial-and-error method of alloying is inefficient.If toxic elements are introduced into products,it is extremely difficult to have them approved by the drug administration department for clinical applications [7].

Crystal-structure based modulation of resistance to stresscorrosion coupled damage (SCCD) is a promising method of overcoming the barrier to the biomedical applications of Mg alloys [8,9].At present,the related studies are still at the preliminary stage of conception and experimental explorations;the high cost of in vivo tests and the difficulty of conducting experiments at small scales result in a lack of data,and the existing empirical correlation models of the corrosion rate and microstructural parameters [10–12]are roughly based on the data fitting of a large number of experiments and a simple multiple-effect linear superposition or weighted average,which cannot objectively and accurately reflect the multiphysical field coupling and multi-scale effects.The absence of low-cost and reliable physical simulation methods limits the accuracy of the quantitative design of biodegradable Mg alloys.Therefore,it is imperative to clarify the mechanisms of SCCD and establish a multi-physical field and multi-scale modeling framework.

The development of SCCD models is hindered by the complexity of materials background and the difficult numerical processing of the multi-physical fields.Recently,some numerical methods,such as the extended finite element method[13],arbitrary Lagrangian Euler method technology [14],and peridynamics [15],have been developed to simulate the moving boundary problems of corrosion.Owing to the inability of the abovementioned methods to handle arbitrary threedimensional geometries,cumbersome implementations,and high computational costs,the related applications are limited.In the phase-field paradigm,the moving boundary equation at the interface is replaced by a differential equation that describes the evolution of the phase-field order parameterϕ.Therefore,the sharp boundary is replaced by a diffusive boundary,which allows for avoiding the explicit processing of the interface conditions.At present,the phase-field method is widely employed for fractures [16–18],fatigue damage[19,20],hydrogen-assisted crack propagation [21–23],corrosion [24–26],and stress corrosion cracking [9,27,28].However,some models are thermodynamically inconsistent,and in some studies,plastic deformations are only linked to the passivation film damage[9],while the mechanical energy driving damage is ignored.The coexistence and interaction of the mechanical damage and degradation during the stress corrosion and corrosion fatigue of biodegradable Mg alloys servicing in the physiological environment are nonnegligible[29].In addition,owing to the mechanical mismatch and electric potential difference,the secondary phases usually result in the damage localization based on the interfacial debonding and galvanic corrosion [13,30]under stress-corrosion coupled loading.The damage localization can significantly influence the damage rate and path,which is clearly different from uniform damage.The insights into the localization formation and development are of great importance to predicting the damage evolution of multiscale structures.However,at present,the majority of galvanic models are based on the electric current density boundary condition characterized by the polarization curves or the test values of the scanning vibrating electrode technique [30–32].This Neumann type boundary condition is valid for the macro-galvanic corrosion,while it is unreasonable for the localized micro-galvanic corrosion in the metals containing secondary phases.The simulation results [30]cannot capture the experimental phenomenon [11]that multiple small pits originated from secondary phases,grew with corrosion proceeding,coalesced with each other,and showed through-thickness progress.Because the rapid evolution and non-uniform distribution of electric current densities in the vicinity of secondary phases are clear,the Neumann boundary condition based on the macroscale surface tests cannot well describe the local charge migration activities in the adjacent area of the secondary phases no matter it is applied on the outer boundaries of the matrix or the secondary-phase interfaces.Therefore,the coupling model of the electric field and stress corrosion in the vicinity of secondary phases is required to be improved to accurately describe the local electrochemical activities.The effects of size,fraction,shape,distribution,electric potential difference,area ratio of the anode to cathode,hardness,elasticity constant,and interfacial energy of the secondary phases based on nontoxic elements on the polarization behavior,damage rate,and path need to be clarified.These mechanisms are important for modulating the corrosion resistance of Mg alloys [5,33,34].

The quantitative crystal design based on the secondary phases of non-toxic elements is a promising method for modulating the corrosion resistance of multi-scale structures under multi-physical fields,and is expected to overcome the existing barrier that is difficult to be overcome using the existing coating technologies and the trial-and-error methods of alloying.In the current study,a phase-field modeling scheme that rigorously complies with the conservation laws and irreversible thermodynamics is established to describe the electrochemomechanical damage,and a local corrosion domain is defined to simulate the local galvanic effect on charge migration and damage localization.

2.Methodology

In this study,the virtual work equation for the deformationdamage (phase field) -mass transfer-electric field coupled framework is first constructed.Mechanical,chemical,and electrical potential energies are then introduced into the Helmholtz free energy.Subsequently,the constitutive equations are derived from the entropy inequality and the weak forms of the governing equations are obtained by substituting constitutive relationships into the virtual work equation.Finally,the multi-physics field dynamic evolution process is numerically solved using finite element discretization and the Newton-Rapson iterative implicit algorithm.

2.1. Theoretical framework of SCCD

2.1.1.Virtual work equation

The current study is aimed at investigating the coupling behaviors of the mechanical and electrochemical fields of biodegradable Mg alloys servicing in the physiological environment based on a phase-field approach.

Considering the conservation of momentum and moment of momentum,phase-field equation for a nonconservative damage field,conservation of mass,and the Gauss theorem for an electrostatic field,generalized equilibrium equations and generalized force boundary conditions can be obtained as follows:

whereσis the stress tensor,Tis the surface force,andnis the surface normal unit vector;Lis the interfacial kinetic coefficient,the negative damage driving forceωand the negative damage fluxζconjugate to the phase fieldϕand phase-field gradient ∇ϕ,respectively,andfis the phase-field microtraction;cis the dimensionless concentration of Mg ions,csolidis the concentration of atoms in Mg metal,Jis the flux defined by a Neumann-type boundary condition,andqis the incoming concentration flux;Dis the electric displacement vector,pis the free charge quantity,andkis the ratio of current density to electrical conductivity.

Following the work [35]for defining the scalar fieldη,the component changes in the kinematics are determined as follows:

Therefore,from the kinematic point of view,the regionΩcan be described by the displacementu,phase-field order parameterϕ,chemical displacementη,and electric potentialφ.The set of virtual fields is denoted as(δu,δϕ,δη,δφ),and the virtual work equation for the coupled system at small deformations is obtained by considering the arbitrariness of the virtual fields:

Operating the upper equation and utilizing Gauss’ divergence theorem yield:

whereε=(∇u+u∇) is the strain tensor for small deformations that can be decomposed into the elastic partεeand plastic partεp,andE=-∇φis the electric field vector.

The details of the coupling systems are presented in(Fig.1): (1) mechanical energy and chemical potential cooperatively drive the corrosion/damage evolution process (L(σ),ω(σ,c),andζ(c));(2)the corrosion/damage of metals results in degradation of the mechanical stiffness(σ=(h(ϕ)+κ));(3) the ion transport is dominated by the concentration and electric potential (J(ϕ,φ));(4) degradation ions,as free charges,affect the electric field distribution (p(c)).Constitutive relationships can be built based on the coupling behaviors.

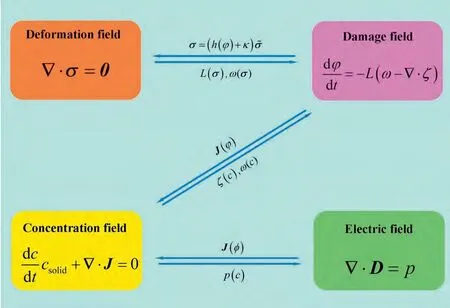
Fig.1.Schematic of multi-physical field coupling.

2.1.2.Dissipated energy rate

Based on the energy conservation law and principal of entropy increment,the dissipated energy rate associated with the irreversible SCCD can be obtained by assuming an isothermal process in the following inequality:

whereris the entropy production rate per unit volume,θis the temperature in Kelvin,extis the power of external work,Φ(εe,ϕ,∇ϕ,c,φ,∇φ,ξ) is the Helmholtz free energy per unit volume,whereinξrepresents the internal variable of plastic deformations,and ˙Φis its rate.

According to the virtual work equation and replacing the virtual fields(δu,δϕ,δη,δφ) by the realizable velocity fields(,,μ,),the inequality can be rewritten as:

2.1.3.Constitutive theory

The total Helmholtz free energy density can be decomposed into mechanical,electrochemical,and interfacial components.The functional form of free energy of each system is defined to derive the thermodynamically consistent constitutive relationships.

The mechanical free energy densityΦMfor the intact configuration is decomposed into elasticΦeand plasticΦpcomponents,both of which are degraded by the phase field,

Here,the degradation functionh1(ϕ) characterizing the transition from the intact solid (ϕ=1) to the damaged phase(ϕ=0) is defined as follows:

It satisfies the conditions thath1(ϕ=0)=0 andh1(ϕ=1)=1.

The elastic strain energy density for the intact configuration is defined as a function of the elastic strainεeand the linear elastic stiffness tensorCin the usual manner,

While the plastic strain energy density for the intact solid is incrementally computed from the plastic strain tensorεpand the stress tensor for the intact configurationas,

whereΦp=is the plastic work for the intact configuration,which is defined as the internal variableξ.

Finally,the isotropic yield and the associated flow rule are applied.Material work hardening is defined by assuming a power-law hardening behavior

whereEis the Young’s modulus,is the equivalent stress for intact configuration,is the accumulative plastic strain,σyis the yield stress,andNis the strain hardening exponent(0 ≤N≤1).

In the corrosion system,the electrochemical free energy densityΦECcan be decomposed into its chemical and electric counterparts:

For anodic dissolution,the chemical free energy densityΦchcan be further decomposed into the energy associated with the material composition and double-well potential energy [24],such that

wherewis the height of the double-well potentialg(ϕ)=ϕ2(1 -ϕ)2.To satisfy the electrochemical requirements,h2(ϕ)=-2ϕ3+3ϕ2.Following the model[36],a free energy density curvatureAis defined,and is assumed to be similar for the solid and liquid phases,cSe=csolid/csolid=1 is the normalized equilibrium concentration for the solid,andcLe=csat/csolidis the normalized equilibrium concentration for the liquid phase,whereincsatis the saturation concentration in the liquid phase.

The electric free energy densityΦelecan be decomposed into the component associated with the free charges and that associated with the electric field distribution:

where the parametersz,F,andEεare the charge number,Faraday constant,and dielectric constant,respectively.

In addition,the interfacial free energy densityΦIis defined as a function of the phase-field order parameter and its gradient as follows:

whereGcis the surface energy density,lcis the interfacial characteristic thickness,andksis related to the energy threshold of damage.

Finally,the constitutive relationships can be readily obtained by satisfying the inequality in Eq.(7),which implies that

Thus,the relationship between the stress and strain can be given as follows:

Accounting for the influence of the phase field and using,the mechanical force balance Eq.(1a) can be reformulated as,

whereκis a small positive parameter introduced to circumvent the complete degradation of the energy and ensure that the algebraic conditioning number remains well-posed.κ=1×10-7is adopted throughout this work to ensure convergence.

The negative damage driving forceωis given by

while the negative damage fluxζis

Substituting the constitutive relationships(20)and(21)into the phase-field balance Eq.(1b) yields the so-called Allen-Cahn equation:

Eq.(22) shows that the material dissolution is governed by the interface kinetics coefficient.The magnitude ofLcan either be considered to be a constant positive number [24]or to be influenced by mechanical straining.In the current study,the film rupture-dissolution-repassivation mechanism interpretation and definition of a mechanochemically enhanced corrosion current density [9]are adopted.The phenomenological description can model the periodic process consisting of the descent of the current density resulting from corrosion product generation and the ascent of the current density resulting from corrosion product dissolution.The phenomenological model is capable of capturing any passivation activities by adjusting the model parameters and is comparatively simple and applicable for engineering prediction.In this model,the interface kinetics coefficient over a time intervaltiis defined as follows:

whereσhis the hydrostatic stress,kmis a function of the local magnitudes ofandσh,kis the film stability parameter,tfis the repassivation time,andt0is the time interval before the next film rupture.

According to Eq.(17) and the Fick law-type relation,the fluxJwithout considering dielectric property degradation can be determined as follows:

Substituting Eq.(24) into the mass-transport balance Eq.(1c),the following field equation is obtained

In this governing equation,ion transport is controlled by both the diffusion and migration effects.The constitutive relationship for the electric field is obtained as follows.

Substituting Eqs.(26) and (27) into the Gauss theorem of the electrostatic field Eq.(1d) yields the following Poisson’s equation for the electric potential:

2.2. Numerical implementation

Fig.2 presents a schematic diagram of the phase-field approximation of the SCCD process.A micro-galvanic corrosion domain is defined by imposing the Dirichlet boundary conditions of free corrosion potentials on Mg matrix boundaries (in purple) and secondary phases (in red).The left,bottom,and right boundaries of the domain possess zero electric current density and the electric potential on these boundaries keeps to be the free corrosion potential of Mg,because corrosion is assumed to vanish outside these boundaries.Outside the top boundary,only the slow uniform corrosion exists,thus the electric current density is weak and the electric potential approximates the free corrosion potential of Mg.Within the domain,a relatively high free corrosion potential is applied on the secondary phases,the distributed electric potential within the domain is higher than the free corrosion potential of Mg,the highest electric current density presents in the adjacent area of precipitates,and the non-uniform electric current density in the vicinity of the secondary phases is different from the macroscale surface test value.In addition,within the domain,the electric conductivity is controlled by the free charges [32,37]:

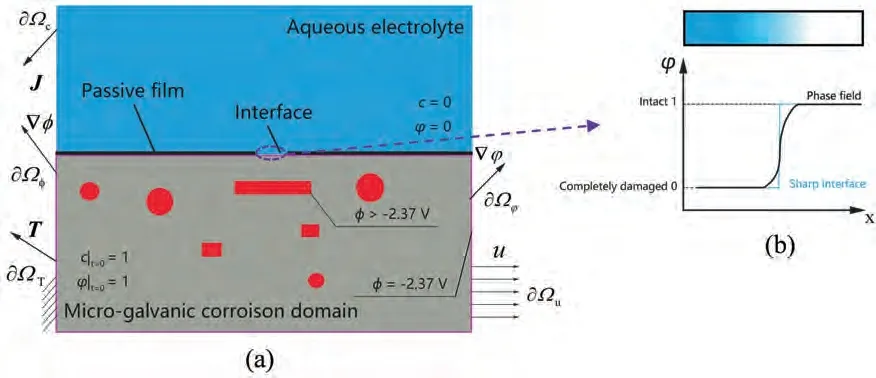
Fig.2.Schematic of the phase-field approximation of the SCCD process:(a)stress-corrosion induced damage under multi-physical fields;(b)diffusive interface versus sharp interface.

whereEσis the electric conductivity,andRis the gas constant.

According to the following Ohm’ law,the evolution of the local electric current density with corrosion proceeding within the corrosion domain can be obtained.

whereIis the electric current density vector.

Combining the equation of continuity+∇·I=0 and the Gauss’ law (Eq.1d) and ignoring the slight change in the electric field within the domain,the relationship for dielectric property and electric conductivity for the domain is simplified as follows:

whereEε0is the initial dielectric constant of Mg.

This relationship interprets the dielectric property decaying with corrosion proceeding,and the mass flux (Eq.24) can be changed into:

where the introduced high-order term includes the second gradient of electric potentials,which extends the Nernst-Planck equation within the local corrosion domain.

The micro-galvanic corrosion domain can be discretized by finite elements,and the SCCD localization can be numerically modelled.

The details of the user element of the SCCD are given in the Appendix A.

3.Results and discussion

In the current study,phase-field modeling of the SCCD is performed at the crystal scale.In Section 3.1,the effects of the refinement and distribution of the precipitates on the diffusion and migration-controlled corrosion rate and path are discussed.In addition,the effects of the long-period stacking order (LPSO) phases on the corrosion rate are analyzed;In Section 3.2,the stress-diffusion corrosion coupled damage process in a C-ring is quantitatively compared with that observed in experiments,and the evolution processes of the stress-diffusion-galvanic corrosion coupled damage localization caused by the soft and hard phases in the prestressed crystal are simulated.

3.1. Secondary phase induced galvanic corrosion

3.1.1.Precipitates

Alloying is an important scheme for the corrosion resistance modulation,strengthening,and toughening of biodegradable Mg alloys.Owing to the low free corrosion potential of Mg,local corrosion is frequently caused by the galvanic effect between the secondary phases containing highpotential elements and the Mg matrix,which dramatically accelerates the degradation of Mg alloys and the loss of mechanical integrity.A large number of reports indicated that the majority of the pitting phenomena are closely related to galvanic corrosion [7].It remains to be determined if it is possible to achieve corrosion resistance optimization through the regulation of secondary phases.In the current study,simulations of a rectangular Mg single crystal with precipitates are conducted to investigate the effect of precipitation on the corrosion rate.First,the corrosion of the Mg single crystal with a single precipitate is simulated.In Fig.3,the initial conditionsϕ=1 andc=1 are applied to the single crystal of size 20×15 μm,the Dirichlet boundary conditionsϕ=0 andc=0 are imposed on the upper surface (basal plane) of the Mg single crystal in contact with the solution,φ=-1.233 V is imposed on the 4×0.5 μm plate-shaped precipitate parallel to the basal plane (Mg17Al12,[38]) (Fig.3a) and vertical to the basal plane (the potential of the vertical precipitate is assumed to be similar to that of Mg17Al12) (Fig.3c),the upper surfaces of the precipitates are 0.5 μm from the upper surface of the single crystal,andφ=-2.37 V is imposed on the outer boundaries (indicated in purple) of the Mg matrix (pure Mg).The material parameters are presented in Table A1.Approximately 9,300 quadrilateral quadratic plane strain elements with reduced integration are used to discretize the models,and the element size is approximately 1/10 the interfacial characteristic thickness (Figs.3b and 3d).

Fig.3.Schematics of initial and boundary conditions of Mg with a single precipitate: (a) single precipitate parallel to basal plane;(b) finite element mesh for (a);(c) single precipitate vertical to basal plane;(d) finite element mesh for (c).

The results show that the addition of a single precipitate significantly accelerates the corrosion rate and induces a strong corrosion localization around the precipitate,thus forming a corrosion pit (Fig.4a and b).Pitting occurs because the large electric potential gradient between the precipitate and Mg matrix can induce strong charge migration when the electrolyte slowly erodes to the vicinity of the precipitate,and the corrosion rate is instantaneously accelerated.For the plate parallel to the basal plane,the corrosion zone around the precipitate rapidly expands into an inverted M-shaped pit at 5Ts(Fig.4a).For the plate vertical to the basal plane,the corrosion zone around the precipitate rapidly expands into a deep V-shaped pit at 5Ts (Fig.4b).The transformation from uniform corrosion to localized corrosion is thus realized.It can be observed that the galvanic corrosion has a significant acceleration effect on the corrosion rate in Mg alloys.As shown in Fig.5,the electric current density in the adjacent area of precipitates,which quickly increases with corrosion proceeding and tends to be constant after 0.4Ts,is non-uniform.The area approaching the upper end of the precipitates is locally corroded at a larger rate compared to that approaching the lower end.Within the corrosion domain,the relationship between electric potential and electric current density is analogous to that in the Tafel polarization curve,and the non-uniformity of the electric current density results in the corrosion localization.Compared to applying the tested electric current density on the outer boundaries of the matrix or the secondary-phase interfaces [30],the proposed model is more accurate and capable of reflecting the corrosion localization.In addition,the statistical results (Fig.6) show that the high-order term in the mass flux,resulting from the enhancement of electric conductivity and the degradation of dielectric property within the corrosion domain,clearly buffers the charge migration and galvanic corrosion.

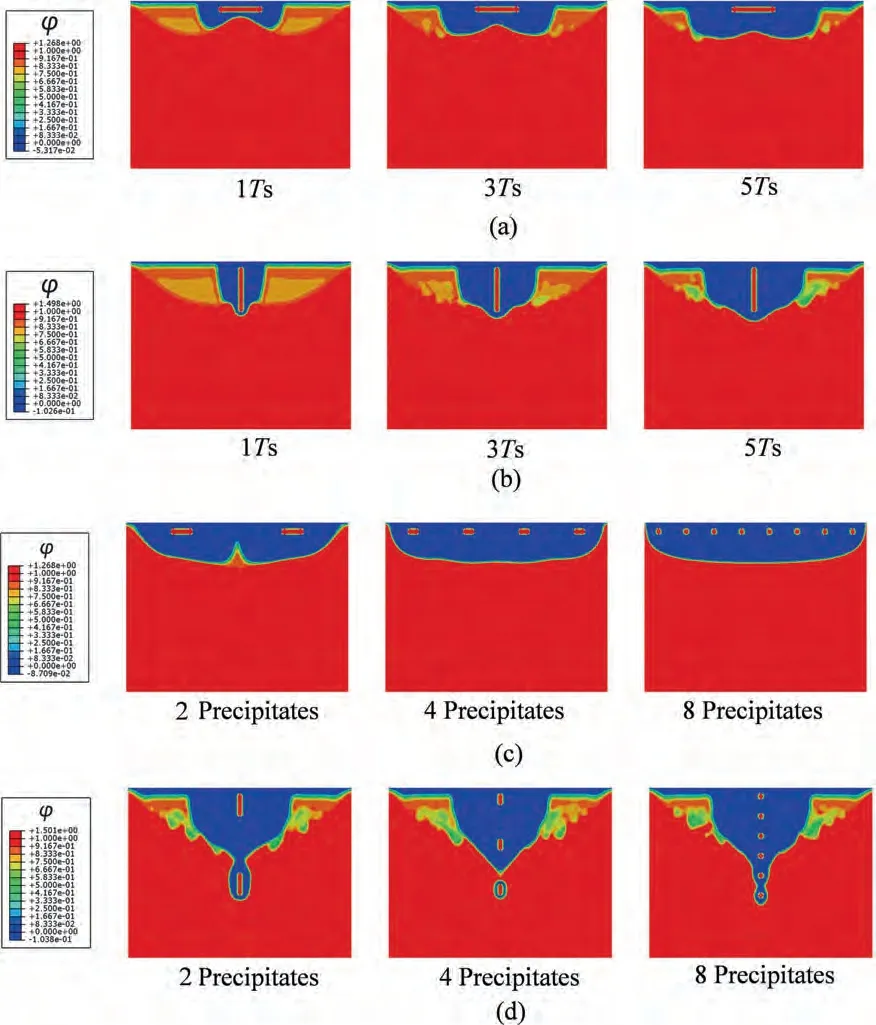
Fig.4.Diffusion and migration-controlled corrosion of Mg with high electrostatic potential precipitates: (a) plate parallel to basal plane;(b) plate vertical to basal plane;(c) different numbers of horizontally refined precipitates at 5Ts;(d) different numbers of vertically refined precipitates at 5Ts.

Fig.5.Electric current density (mA/mm2) in Mg with high electrostatic potential precipitates: (a) plate parallel to basal plane;(b) plate vertical to basal plane.

Fig.6.Statistical results of corrosion interface nodes of Mg crystal with a single precipitate parallel to basal plane at 5.2Ts: (a) dimensionless concentration c;(b) phase-field order parameter ϕ.

Furthermore,to investigate the effect of precipitate refinement and distribution on the corrosion rate,while maintaining the volume fraction as constant,the single precipitate is refined horizontally into two,four,and eight precipitates and vertically into two,four,and eight precipitates.The corrosion evolution of refined precipitates is simulated.

As shown in Fig.4c,diffusion from the upper surface of the matrix can trigger charge migration around the two horizontally refined precipitates when diffusion-controlled corrosion occurs near the precipitates,and the strong corrosion localization results in two pits that can coalesce with each other.For the four precipitates (Fig.4c),the smaller and closer precipitates buffer the electric potential gradient between the precipitates,thus decreasing the corrosion rate and forming a wider and shallower pit.For eight precipitates (Fig.4c),the electric potential gradient between precipitates is lowest,the corrosion rate further decreases,and the pit possesses the width of the entire upper surface of the matrix and the lowest depth.The statistical results in Fig.10a indicate that,owing to the precipitate refinement along the horizontal direction,the dimensionless corrosion rate decreases significantly,and the corrosion depth is simultaneously reduced.In addition,the corrosion rate gradually drops down with time because the localized corrosion switches into uniform corrosion after the vicinity of the precipitates is completely corroded.

As shown in Fig.4d,the diffusion from the upper surface of the matrix can first trigger charge migration in the adjacent area of the upper surface of the upper precipitate when diffusion-controlled corrosion occurs near the precipitate,and the strong corrosion localization results in a deep pit.Then,owing to the electric potential gradient around the lower precipitate,charge migration is activated around the lower precipitate when diffusion occurs near it.The upper pit can rapidly link to the lower corrosion zone,and the corrosion rate and depth are much greater than those of a single precipitate.For four precipitates (Fig.4d) and eight precipitates (Fig.4d),the corrosion zones around the precipitates coalesce with each other at a great speed,and the systems rapidly lose their mechanical integrity.The statistical results presented in Fig.10b indicate that,owing to the precipitate refinement along the vertical direction,the dimensionless corrosion rate significantly increases,and the corrosion depth is simultaneously enhanced.In addition,the corrosion rate gradually drops down with time.A corrosion path can form along the vertically distributed precipitates,which is quite different from the case of uniform corrosion.Galvanic corrosion significantly accelerates the corrosion rate and depth,usually resulting in the sudden failure of structures.In addition,based on defect-controlled elemental segregation,it is possible to optimize the corrosion resistance and balance the mechanical-electrochemical properties in biodegradable polycrystalline Mg alloys,which requires further quantitative evaluation based on the application of the proposed model to polycrystalline structures.

In most cases,secondary phases are cathodic.However,there are fewer anodic secondary phases such as Mg2Ca and Mg41Nd5in Mg alloys [39,40].Different potentials are imposed on the same precipitate in order to clarify the potential difference effect on the galvanic corrosion localization.For the precipitate with the same potential as Mg,no galvanic corrosion happens.For the precipitate with the higher potential (-1.233 V) than Mg,the obvious galvanic corrosion localization resulting from the migration effect happens near the precipitate (Fig.7a).For the precipitate with the lower potential (-3.507 V) than Mg,the precipitate can protect the cathodic matrix near it from corrosion (Fig.7b).Some methods [7,39]based on the sacrificing anodes have been proposed to enhance the corrosion resistance.

Fig.7.Comparison of corrosion induced by anodic and cathodic precipitates: (a) cathodic precipitate;(b) anodic precipitate.

The precipitate refinements along the horizontal and vertical directions have a conflicting effect on the corrosion rate and depth,and the potential difference leads to the significant difference of corrosion rate.To optimize the corrosion resistance and mechanical integrity of biodegradable Mg alloys serving in the physiological environment,the precipitates with higher potentials should be reasonably refined and distributed,and the precipitates with lower potentials can be the sacrificing anodes to protect Mg from corrosion.The proposed model can be used to numerically predict and design the corrosion rate and depth.Whatever the potentials and elements of secondary phases are,the proposed theoretical and numerical framework is capable of capturing the corrosion induced by different secondary phases.Undoubtedly,the proposed framework can also handle the corrosion problem in the Mg matrix with several intermetallic compounds [41].

Furthermore,to model the realistic pitting phenomenon,the single precipitate is refined into 16 fine precipitates,which are randomly distributed in the Mg single crystal.As shown in Fig.8a,the Dirichlet boundary conditionsϕ=0 andc=0 are imposed on the upper surface in contact with the solution,φ=-1.233 V is imposed on all the precipitates,φ=-2.37 V is imposed on the outer boundaries of the crystal,and the initial conditions ofϕ=1 andc=1 are applied to the 20×15 μm Mg single crystal.The material parameters used in this study are listed in Table A1.Approximately 8,757 quadrilateral quadratic plane strain elements with reduced integration are used to discretize the model,and the element size is approximately 1/10 the interfacial characteristic thickness (Fig.8b).

Fig.8.Schematic of initial and boundary conditions of Mg with refined random precipitates: (a) random distribution of refined precipitates;(b) finite element mesh.

Fig.9a shows that,at the early stage of corrosion (0.01Ts),owing to the charge migration under galvanic effect,some pits are rapidly formed around the precipitates near the upper surface.Subsequently (0.1-0.5Ts),the corrosion zones around the lower precipitates form one after another owing to the diffusion and migration cooperated effect.During 1-5Ts,the proposed model clearly simulates the formation of microgalvanic corrosion localization in the adjacent area of the precipitates,pit growth and coalescence,and through-thickness corrosion progress.These details and progresses (3D simulation results are given in the Appendix B) are in good accordance with the previous observations[11](Fig.9b).As shown in Fig.10c,the corrosion rate of the crystal with randomly distributed precipitates is lower than that with eight vertical refined precipitates and higher than that with eight horizontal refined precipitates.

Fig.9.Simulations and experiments of corrosion localization in Mg with randomly distributed precipitates:(a)simulations of diffusion and migration-controlled corrosion;(b) the energy-dispersive X-ray spectroscopy (EDX) analysis indicates that pitting corrosion preferentially took place in the vicinity of secondary phases with a higher free corrosion potential;with corrosion proceeding,multiple small pits formed at 3 h;pits grew and coalesced with each other to form a much larger pit at 12 h;the large pit showed significant through-thickness progress at 40 h.

Fig.10.Dimensionless corrosion rate versus dimensionless time: (a) different numbers of horizontal precipitates;(b) different numbers of vertical precipitates;(c) comparison among random distribution,horizontal refinement,and vertical refinement.

3.1.2.LPSO phases

It has been reported that LPSO phases in rare-earth Mg alloys cannot only significantly enhance mechanical properties,but also modulate corrosion resistance [42,43].To investigate the effect of LPSO phases on corrosion rates,the corrosion of a 20×15 μm rectangular Mg single crystal with two types of LPSO phases is simulated.As shown in Fig.11,the Dirichlet boundary conditionsϕ=0 andc=0 are imposed on the upper surface in contact with the solution,φ=-1.98 V is applied to the LPSO phase,φ=-2.37 V is applied to the outer boundary of the single crystal,and the initial conditionsϕ=1 andc=1 are applied to the single crystal.The two types of LPSO phases are 18R formed at the grain boundaries (Fig.11a) and 14H as the laminae transmitting within grains (Fig.11c),respectively.The material parameters used in this study are listed in Table A1.Quadrilateral quadratic plane strain elements with reduced integration are used to discretize the models,and the element size is approximately 1/10 the interfacial characteristic thickness (Figs.11b and d).

Fig.11.Schematics of initial and boundary conditions of Mg with two types of LPSO phases [42]: (a) 18R-LPSO phase;(b) finite element mesh for 18R with 4,560 elements;(c)14H-LPSO phase;(d) finite element mesh for 14H with 4,159 elements.

As shown in Fig.12a,the 18R-LPSO phase acts as a barrier to corrosion,even if it possesses a higher electric potential than the Mg matrix.Corrosion gradually encompasses the entire LPSO phase and slowly diffuses downward,eventually exhibiting an effect similar to uniform corrosion.At 5Ts,the corrosion depth is relatively low.As shown in Fig.12b,the electric potential difference between the laminar 14H-LPSO phase and the matrix can result in a galvanic effect,thus significantly accelerating the corrosion.The diffusion and migration cooperated effect rapidly corrodes the entire LPSO phase and its surroundings.At 5Ts,the corrosion almost penetrates the entire Mg crystal,thus causing a significant loss of mechanical integrity and load-bearing capacity.In addition,at 5Ts,the dimensionless corrosion rates of 14H and 18R are approximately 9.6 and 2.2 times of the uniform corrosion,respectively,and the corrosion rate and depth of Mg with 14H are much greater than those of the Mg with 18R (Fig.13).The simulation results indicate that the corrosion resistance of Mg containing 18R-LPSO phase is much better,which is consistent with the experimental results [42].Certain heat treatments can transform various types of LPSO phases into another [43],thus the manipulation and the proposed simulation scheme are capable of optimizing and predicting the corrosion rate and depth of polycrystalline biodegradable Mg materials and structures with LPSO phases.

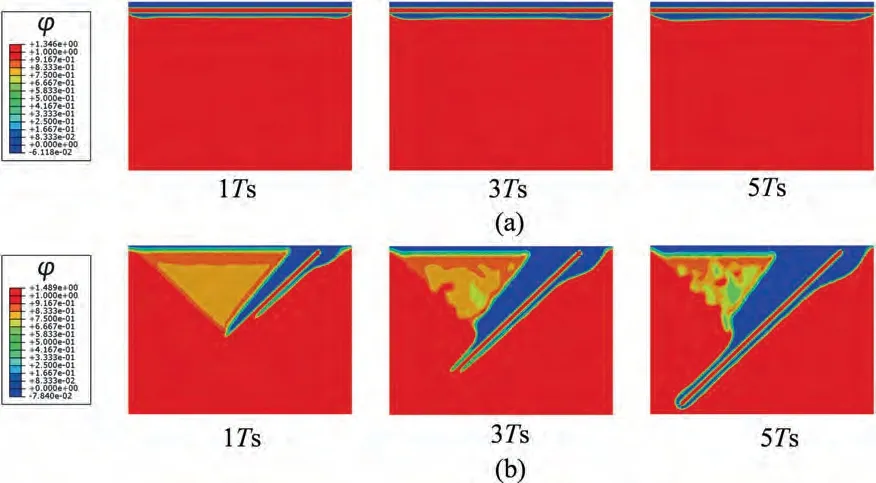
Fig.12.Diffusion and migration-controlled corrosion of Mg with LPSO phase: (a) 18R-LPSO phase;(b) 14H-LPSO phase.

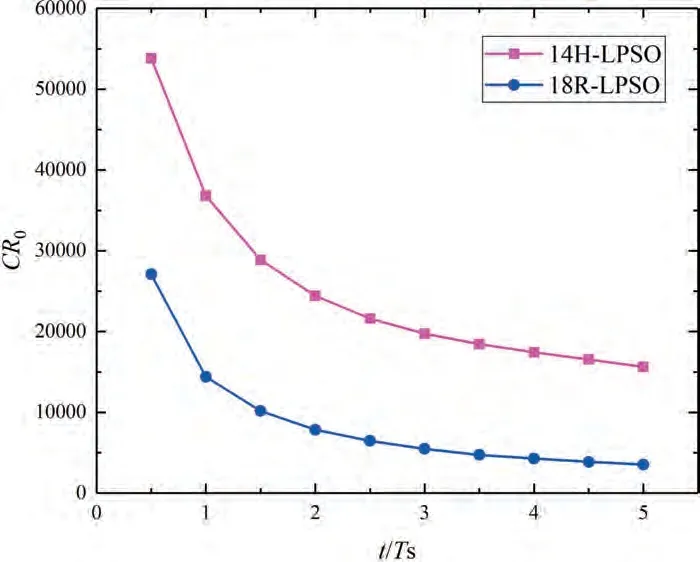
Fig.13.Dimensionless corrosion rate versus dimensionless time for different type of LPSO phases.

3.2. SCCD

3.2.1.Validation of SCCD model

The physiological environment contains a relatively high concentration of chloride ions [44]and may present a low pH owing to post-traumatic inflammation [2].In addition to the attack of corrosive ions,the implants or devices,such as sutures,anastomotic nails,stents,and bone joints,have to bear large plastic deformations and/or multi-axial fatigue/impact loading [45–47].Therefore,biodegradable Mg alloys servicing in the physiological environment are exposed to a strong coupling environment of harsh corrosion and severe mechanical loading,which usually results in their sudden failure.It is necessary to develop a numerical model that rigorously obeys the conservation laws and irreversible thermodynamics of the complicated physical and chemical processes to objectively and accurately simulate the SCCD at the crystal scales of biodegradable Mg alloys.Because the propose theoretical and numerical framework is independent of material properties and features,and both Mg and steel undergo elastoplastic deformations and anodic dissolution during the SCCD,it is convincing to validate the correctness of the driven force constitution and constitutive relationships with a classic case of Q345R steel C-ring specimens damaged in a hydrofluoricacid corrosive environment.Because the corrosion products are mainly fluorides (rather than oxides) and the density of the film is insufficient to prevent the attack of aggressive ions[48],the effect of film passivation is negligible.

As shown in Fig.14a,the C-ring is subjected to a constant strain by tightening the bolt centered on the ring diameter,and the circumferential stressσsat the top of the sample is used to measure the load.In the experiment,the C-ring specimen is exposed to 40 wt.% hydrofluoric acid at room temperature,with a pit (location A) as the crack initiation location.

Fig.14.Schematic of the tightened C-ring: (a) geometry;(b) finite element mesh,initial and boundary conditions,and dimensions.

The specimen has an inner diameter of 20 mm and an outer diameter of 25 mm (Fig.14b).Vertical and horizontal displacement constraints are imposed on the left side,and a Dirichlet displacement boundary condition is applied on the right side to impose the horizontal displacement component of the bolt when it is tightened.To maintain consistency with the experiments,the mechanical and corrosion parameters (Table A2) for the experimental Q345R steel are used.For the whole sample,approximately 11,093 quadrilateral quadratic plane strain elements are used,and the largest element size is 0.05 mm.The SCCD area in front of the pit is discretized by denser elements of sizes less than or equal to 0.005 mm.It should be noted that full integration is applied to avoid the severe distortion of elements during deformations and to maintain sufficient accuracy.To capture the damage process,the Dirichlet boundary conditionsϕ=0 andc=0 are imposed on the surface of a semi-elliptical pit at the top,and the initial conditions ofϕ=1 andc=1 are applied to the C-ring.

A quantitative comparison between the proposed model and the experiments for different stress levels is presented in Fig.15.Numerical results are shown in terms of the length of the damage region (the vertical distance from the top to the crack tip),including crack initiation from the pits and crack propagation,as a function of time.To accelerate the simulation,the simulation time cannot be the true experimental time by settingL0.A time calibration must be performed.In each simulation,the segment between two initial experimental points is first selected,then the entire simulation time is stretched according to the time proportion of the selected segment,and a total of 16 simulation points are obtained from the FEM results.The simulation results are in good agreement with the experimental results [48]atσs=1.05σy,σs=0.80σy,andσs=0.55σy.In addition,the simulated morphology of the crack originating from a surface pit at stress levelσs=0.80σyand experimental timet=210 min basically coincides with the experimental results.Therefore,the proposed SCCD model can be used to further evaluate the damage localization induced by secondary phases.

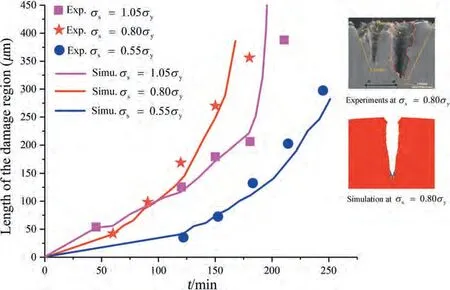
Fig.15.Experimental [48]and simulated lengths of the SCCD region versus time t for three different mechanical stress levels of σs=1.05σy, σs=0.80σy,and σs=0.55σy(the embedded figures are the experimental and simulated morphologies at stress level σs=0.80σyand experimental time t=210 min).

Furthermore,to determine the effect of stress on the damage,the stress concentration and gradient of C-ring during the SCCD process are given in Fig.16.The stress gradient is characterized by the density of the contour lines.As shown in Fig.16,with the growth of the crack,the stress concentration at the crack tip becomes more significant,and the denser contour lines indicate the greater stress gradient.Therefore,as the SCCD proceeds,the stress gradually takes the leading role,dominating the damage path and rate.

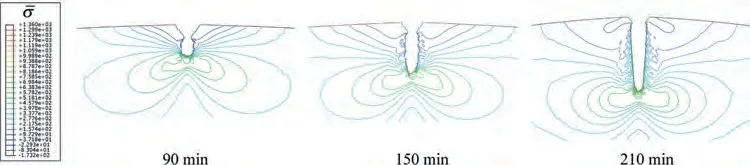
Fig.16.The contour lines of equivalent stress for C-ring at σs=0.80σy.

3.2.2.Damage localization induced by secondary phases

In general,stress corrosion cracking,as a typical mode of SCCD,is the sudden brittle damage of materials under tensile stresses in corrosive environments.In addition,damage localization caused by the cooperative effect of stress,diffusion,and galvanic corrosion also frequently occurs and results in severe failure during both large plastic deformations and cyclic deformations of the materials servicing in corrosive environments.Medical sutures of Mg alloys are designed to slowly degrade under high tensile pre-stress in human tissues.Sutures would not effectively suture wounds if they got relaxed by premature damage localization.In this section,the SCCD localization of a single crystal of Mg with a circular secondary phase under pre-stress stretching is simulated.The rectangular region of size 6×3.5 μm is presented in Fig.17.The normal displacements of 0.3 μm are first applied on the left and right sides of the region to simulate the prestressed process.To simulate the subsequent SCCD,the Dirichlet boundary conditionsϕ=0 andc=0 are imposed on the upper surface ({10-10} plane) in contact with the solution,φ=-1.82 V is imposed on the secondary phase(rod-shaped MgZn2parallel to {10-10} plane and veritcal to basal plane,[49,50]),andφ=-2.37 V is imposed on the outer boundaries of the single crystal.The initial conditions ofϕ=1 andc=1 are applied to the entire rectangular region.

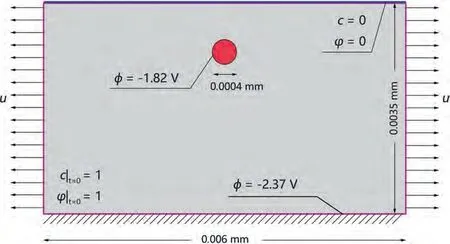
Fig.17.Schematic of initial and boundary conditions of Mg with a circular secondary phase subjected to a tensile prestress.

The mechanical and corrosion parameters used are listed in Table A3.It should be noted that a larger interfacial kinetic coefficientL0=100 mm2/(N ·s) compared to that used in the pure galvanic corrosion of Mg (Section 3.2) is used to accelerate the simulation.The Young’s modulus and yield stresses of the soft and hard phases in this model are set as 1/10 and 10 times that of the Mg matrix,respectively.The element size near the interface between the secondary phase and the matrix is controlled as 1/20 the interfacial characteristic thickness and the size of the rest is approximately 1/10.In total,16,296 quadrilateral quadratic plane strain elements with reduced integration are used for the discretization.

It can be clearly observed from Fig.18 that,before the corrosion starts,the damage around the circular phases occurred owing to the elastic and plastic mismatch under the tensile prestress.The upper surface of the single crystal with a hard phase deforms to an upward convex shape,and the damage order parameter decreases by 0.989 (Fig.18a).The upper surface of that with a soft phase deforms to an downward concave shape,and the damage order parameter decreases by 0.915 (Fig.18b).The soft phase results in greater damage as compared to the hard phase.

Fig.18.Stress-induced damage localization of Mg with a secondary phase: (a) hard phase;(b) soft phase.

The process of SCCD localization is presented in Fig.19.After the corrosion starts,the upper surface is first slowly corroded by the diffusion effect.Because the existing mechanical damage inevitably results in rapid corrosion in the vicinity of the secondary phases,charge migration is then triggered owing to the electric potential gradient between the secondary phases and the matrix,and the coupled damage gradually encircles the entire secondary phases,thus causing strong damage localization and forming vase-shaped corrosion pit morphologies (Figs.19a and b).Compared to the corrosion pit of the unstressed Mg single crystal with a secondary phase (Fig.19c),the corrosion pit of the prestressed Mg single crystal with a hard phase is similar to a vase with a wider belly.The corrosion pit of the prestressed Mg single crystal with a soft phase not only has a wider belly but also a large bottom,thus presenting the greatest damage.In addition,the damage rate results (Fig.20) show that at the early stage of corrosion,the order of the damage rate is as follows: prestressed matrix with a soft phase>prestressed matrix with a hard phase>unstressed matrix with a secondary phase.It should be noted that the difference in the damage rates gradually decreases with time.

Fig.19.Stress-corrosion induced damage localization of Mg with a secondary phase: (a) hard phase;(b) soft phase;(c) unstressed crystal.

Fig.20.Dimensionless damage rate versus dimensionless time for different corrosion conditions of Mg alloy with secondary phases.

To determine the effect of stress on the damage,the stress concentration and gradient around precipitates are given in Fig.21.As shown in Fig.21a and b,at 0.01Ts,owing to the effects of stress and charge migration,the local damage occurs at the interface between the precipitate and matrix,leading to a filamentous gap.The strong stress concentration and great stress gradient are generated at the gap tips under the pretensile stress.As the SCCD proceeds (0.05Ts),the migration effect leads to the rapid dissolution of the matrix in the adjacent area of the precipitate,the rapid expansion of the gap,and the formation of a crescent-shaped gap above the precipitate.At 0.1Ts,the further expansion of the gap geometry results in the significant reduction of stress concentration and stress gradient.Therefore,in the diffusion-migration-stresscontrolled SCCD process,the migration effect gradually takes the leading role and significantly weakens the stress concentration and gradient.

Fig.21.The contour lines of equivalent stress for Mg crystal with: (a) a soft precipitate;(b) a hard precipitate.

The prestress induced mechanical damage along with the diffusion and migration-controlled corrosion can result in strong damage localization,which is more harmful to the biodegradable Mg structures than any single effect,especially at the early stage of service.Therefore,for some medical Mg alloys designed for short-term service (such as sutures,staples,and other medical devices for which corrosion resistance is particularly important at the early implantation period),the appearance of soft phases with high electric potential or cavities should be prevented as far as possible,to ensure that the implants cannot be relaxed by premature damage localization and that they possess sufficient designed service life in the physiological environment [47].In addition,the cyclic loading is also common for Mg structures servicing in biological environment.The simulation for the SCCD during the corrosion fatigue under cyclic loading is given appendix C.

4.Conclusions

A thermodynamically consistent phase-field model is developed for the SCCD localization induced by secondary phases.By imposing the Dirichlet boundary conditions of free corrosion potentials,the micro-galvanic corrosion domain is set.Considering the evolution of electric conductivity and dielectric property with the corrosion proceeding and building the multi-physical field finite element framework of the proposed model,the localization in the diffusion and migrationcontrolled corrosion and the SCCD of the biodegradable Mg alloys servicing in the physiological environment are numerically simulated.Within the corrosion domain,the Nernst-Planck equation of mass transfer is extended by considering the buffering effect of the second gradient of electric potentials on charge migration.The quantitative evaluation of the coupled damage depth varying with corrosion time and the crack morphology of the C-ring are in good agreement with the classical experiments.Three crystal-scale cases are conducted to further validate the proposed model and offer some insights into the damage localization process and valuable inspiration for resistance design.The following conclusions can be drawn:

(1) For diffusion and migration-controlled corrosion,corrosion localization,followed by pit growth,pit coalescence,and through-thickness progress,significantly accelerates the corrosion rate.The refinements of the precipitate with the higher potential along the horizontal and vertical directions present a conflicting effect on the corrosion rate.Reasonable refinement is of great importance to the corrosion rate,and the segregation mechanism can be used to control the corrosion path.Conversely,the precipitate with the lower potential can act as the sacrificing anode to protect the Mg matrix from corrosion.In addition,18R-LPSO phase and 14HLPSO phase exhibit the opposite effects on the corrosion resistance.18R-LPSO phase acts as a protective barrier role to significantly improve the corrosion resistance of Mg,while 14H-LPSO phase can accelerate the corrosion of the Mg matrix.The buffering effect,which results from the dielectric property degradation in the vicinity of secondary phases and accompanies with the migration,is capable of slowing down the corrosion rate and is promising for the restriction of the corrosion localization.

(2) For the SCCD localization around the secondary phases in Mg alloys,the soft phases,with a higher electric potential than that of the matrix and worse mechanical damage compared to hard phases,possess weaker damage resistance and are prone to becoming the starting points of structural failure at the early stage of service in the physiological environment.At the early stage of the SCCD,the mechanical damage driven by the mechanical work accumulation resulting from the elastoplastic mismatch around the secondary phases can dramatically accelerate corrosion and result in severe damage localization.However,with the SCCD proceeds,the stress concentration and gradient can be weakened by the expansion of the gap geometry between the precipitate and matrix.The damage resulting from the coupled effect is much greater than that due to any single effect.

The current study provides a theoretical framework and its numerical scheme for the quantitative evaluation of SCCD localization.The proposed model,which can be further coupled with cathodic reactions,hydrogen-induced damage,microstructural evolution,and cyclic fatigue loading,is expected to be applied to the design of multiscale structures of Mg alloys or other materials servicing in corrosive environments.

Acknowledgements

The authors are grateful for the support from the National Natural Science Foundation of China (Nos.11872216 and 12272192),the Natural Science Foundation of Zhejiang Province (No.LY22A020002),the Natural Science Foundation of Ningbo City (No.202003N4083),the Scientific Research Foundation of Graduate School of Ningbo University,and Ningbo Science and Technology Major Project (No.2022Z002).

Appendix A

First,the weak forms of the governing Eqs.(19),(22),(25),and (28) are formulated.

Table A1 Material parameters for corrosion.

Similarly,the associated gradient quantities ε(4×1),∇ϕ(2×1),∇c(2×1),∇φ(2×1),and ∇∇φ(4×1)are discretized as follows:

where the standard strain–displacement matrix,gradient matrix B(2×i),and second gradient matrix Bs(4×i)are applied.

The weak form balances Eqs.(A1)-(A4) are discretized in time and space such that the resulting discrete equations of the balances for the displacement,phase field,concentration,and electric potential can be expressed as the following residuals:

where the superscript()(n+1)denotes the(n+1)-th time step,dtis the time increment,Ωeis the element domain,∂Ωeis the element boundary,and ∇∇φ(4×1)should be rearranged into a second-order matrix.

Subsequently,the tangent stiffness matrices are calculated as follows:

where Cep(4×4)is the elastic-plastic equivalent stiffness matrix.

Finally,the linearized finite element system can be expressed as follows:

The finite element system is solved by employing a time parametrization and an incremental-iterative scheme in conjunction with the Newton–Raphson method.According to the elemental orders and the numbers of nodes and integration points,the residual and stiffness matrices are built for the current step.The numerical model is implemented in the finite element package ABAQUS through a user element subroutine.

To ensure that the ion migration is inactive in the pure solid phase,the electric charge migration effect is shut down by settingz=0 whenϕ≥0.9.To keep the free charge quantity nonnegative and no more than the highest value,the values ofcon integration points are limited in the range of [0,1].In addition,to avoid the increase in the phasefield order parameterϕat the beginning of the simulation,the Heaviside function that ensures that the driving force of damage is less than or equal to zero is applied.

In addition,based on the weight loss methodCR=[48],in the current study,=mlc2can be defined as the corroded/damaged area,the dimensionless coefficientKis set as 8.76×104,A=nlccan be defined as the equivalent length of the upper surface of the corroded area,andt=pTs can be defined as the corrosion time,whereinis introduced as the reference time.Thus,the corrosion/damage rate can be formulated asCR=CR0L0G{0001},whereinis a dimensionless corrosion/damage rate.The relationship between the dimensionless corrosion/damage rateCR0and dimensionless timepis employed to characterize the evolution of the corrosion/damage rate with time in the simulation results.It should be noted that the real corrosion/damage rate and time can be obtained by the calibrating the reference timeTs and kinetic coefficientL0based on the corrosion depth and corresponding time in a standard experiment.

The parameters for simulations are listed below:

Appendix B

The simulated surface morphologies of the corroded Mg with randomly distributed precipitates are shown in Fig.B1.At the early stage of corrosion (0.01Ts),owing to the charge migration under galvanic effect,some pits are rapidly formed around the precipitates.As corrosion proceeds (0.2-3Ts),the proposed model clearly simulates the formation of microgalvanic corrosion localization in the adjacent area of the precipitates (0.2Ts),pit growth (1Ts),and coalescence (3Ts).The simulation results of the surface morphologies are also in good agreement with the experimental observations.However,the through-thickness progress and local corrosion activities under the surface are not conveniently shown and observed in the 3D simulation,and the more important point is that,the computational efficiency of the 3D model with more nodes and integration points is much lower than that of 2D.

Fig.B1.Simulated surface morphologies of the corroded Mg with randomly distributed precipitates: at the early stage of corrosion (0.01Ts),some pits are rapidly formed around the precipitates;as corrosion proceeds (0.2-3Ts),the proposed model clearly simulates the formation of the micro-galvanic corrosion localization in the adjacent area of the precipitates that are represented by the absent elements (0.2Ts),pit growth (1Ts),and coalescence (3Ts).

Appendix C

As shown in Fig.C1a,with increasing number of the cyclic loading,the accumulation of plastic work gradually intensifies damage.Because the plastic work contributes to the driven force of SCCD,the damage under the cyclic loading (Fig.C1c) is much severer than that under prestress(Fig.C1b).