径向螺旋槽空气轴承起飞速度与承载能力试验研究

韩原臻，殷玉枫，王嘉誉

(太原科技大学机械工程学院，山西太原 030024)

空气轴承，即采用气体润滑的轴承。自1958年英国原子能机构(UK Atomic Energy Establishment)提出第一台支持涡轮机械的气体轴承以来，气体轴承在涡轮压缩机、燃气轮机和涡轮增压器/膨胀器等各种应用中显示了其优势。1913年，HARRISON[1]在保留连续性方程中的密度项，并且引用等温条件的假设推导出可压缩雷诺方程，并给出无限长气体滑块轴承和轴颈轴承的解，为以后的气体动压润滑技术研究奠定了基础，从而使得气体润滑轴承走上了快速发展的道路。之后以AUSMAN、PAN、GROSS、CASTELLI和LUND等的研究最具有代表性[2-6]，他们研究采用线性摄动法求解动态雷诺方程，从而求出4个刚度系数和4个阻尼系数，在此基础上给出了气体轴承的稳定性判据。

目前，气体轴承在4个领域里占有绝对的应用优势，即高速支承、低摩擦低功耗、高精度支承和特殊工况下的支承[7]。空气轴承是保证转子稳定运行和快速达到超高速运转的重要部件，与其他滚珠轴承和滑动轴承不同，空气轴承仅在启动和停止时存在摩擦，当轴承到达起飞速度后，转子不再存在摩擦损耗，所以研究不同载荷下的起飞速度就显得尤为重要。随着螺旋槽气体轴承起飞速度与承载能力研究的深入，CHUN和KHONSARI[8]分析了在不同载荷下空气轴承的起飞速度，提出了预测起飞速度的方程式，并将其结果与沃格尔波尔方程进行比较。LIU等[9]对人字形沟槽气体轴承支撑的刚性转子进行了非线性研究，结果表明，随着静载荷的增加，空气轴承稳定性会提高。SALANT等[10]开发了一种数学模型，用于预测气体机械密封的瞬态行为。

我国对于气体润滑技术的研究相对来说起步较晚，从20世纪50年代才开始着手于气体轴承的研究，并取得了一定的成果[11]。其中具有代表性的包括周恒和刘延柱[12]编著的《气体动压轴承的原理及计算》以及王云飞编著的《气体润滑理论与气体轴承设计》[13]等，这些书籍的出版大大推动了我国气体轴承的研究。戚社苗等[14]将气体动压润滑雷诺方程通过数学变换成标准的椭圆型偏微分方程，采用MATLAB PDE工具箱为求解器，编制计算程序，实现了动压气体轴承性能的高精度计算。

起飞速度与承载能力是螺旋槽动压气体轴承设计和使用中的重要性能指标。螺旋槽动压气体轴承是通过气膜的弹性势能来支承载荷的，由于启动过程中转子和轴承表面之间无法形成有效的动压气膜，转子和轴承会直接接触，处于干摩擦状态。随着转速的升高，转子和轴承表面之间形成润滑气膜，转子从干摩擦状态转变为气体润滑状态。起飞转速就是判断特定载荷下气体轴承是否进入气体润滑状态的直接标志。因此如何确定空气轴承的起飞转速成为气体轴承研究中的关键问题[15]。

目前国内对于螺旋槽空气轴承起飞速度与承载能力的研究较少。本文作者以径向螺旋槽空气轴承为研究对象，通过建模求解其微分方程后对设计的轴承进行试验与分析，测试了其不同承载下的起飞转速，为后续螺旋槽空气轴承研究及其工程应用提供了理论与实践基础。

1 螺旋槽径向动压空气轴承

螺旋槽动压气体轴承，以其承载大(特别是高速下)、功耗低、高速稳定性好等特点，远优于其他类型动压气体轴承。图1所示为螺旋槽空气轴承结构示意图，其中L为轴颈长度，R为轴颈半径，β为螺旋槽槽角，Ly为螺旋槽槽长，b为槽宽，ω为旋转角速度。

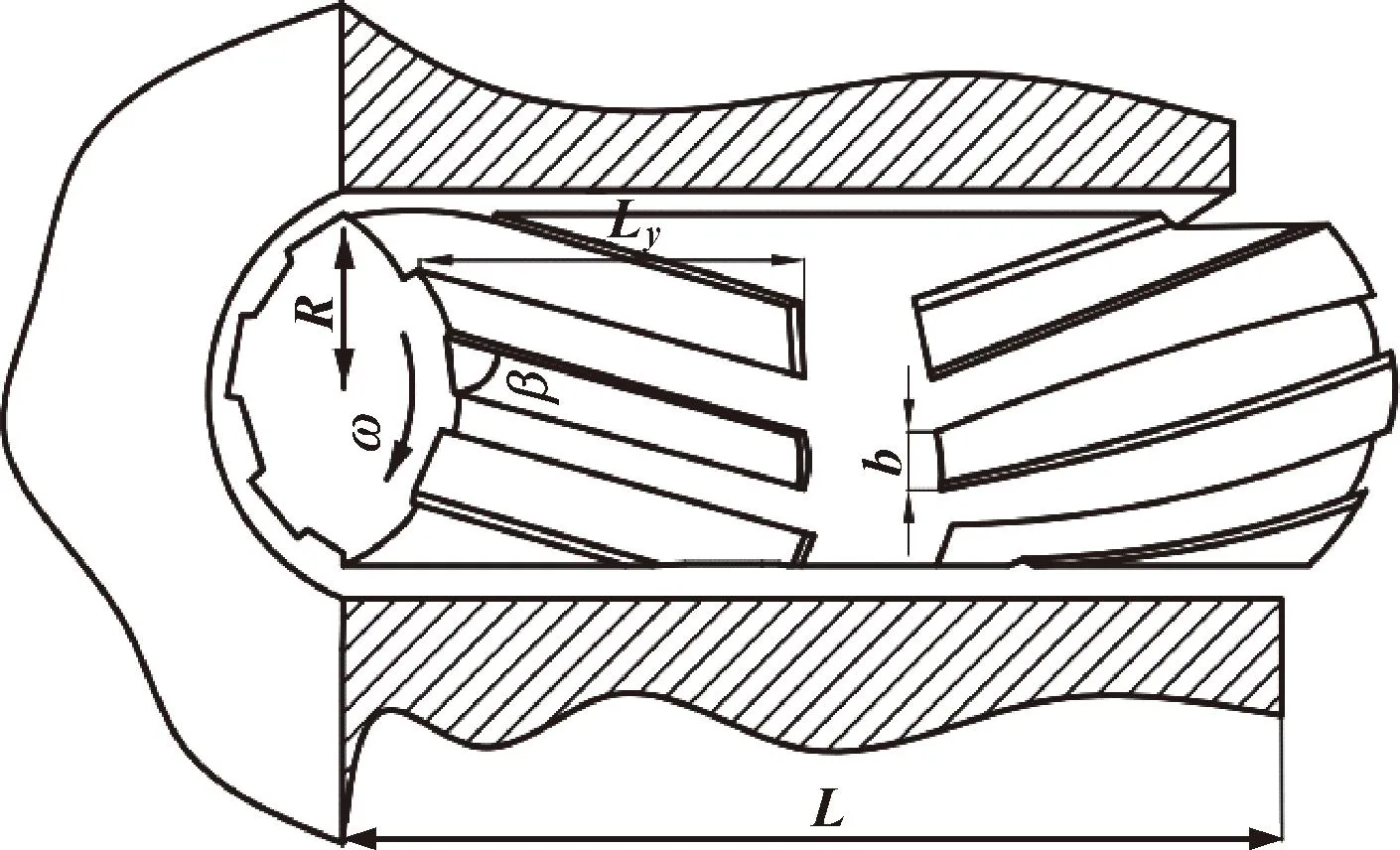
图1 螺旋槽空气轴承结构示意

图2所示为文中试验用螺旋槽空气轴承工作原理图，其中W为轴承负载，轴承间隙从A到B逐渐变窄，并在该段形成楔形间隙。按照承载力最优进行设计，以承载力分量Wcosφ达到最大值为优化条件，不取总承载力作为目标函数，也可同时兼顾轴承保持较好稳定性。

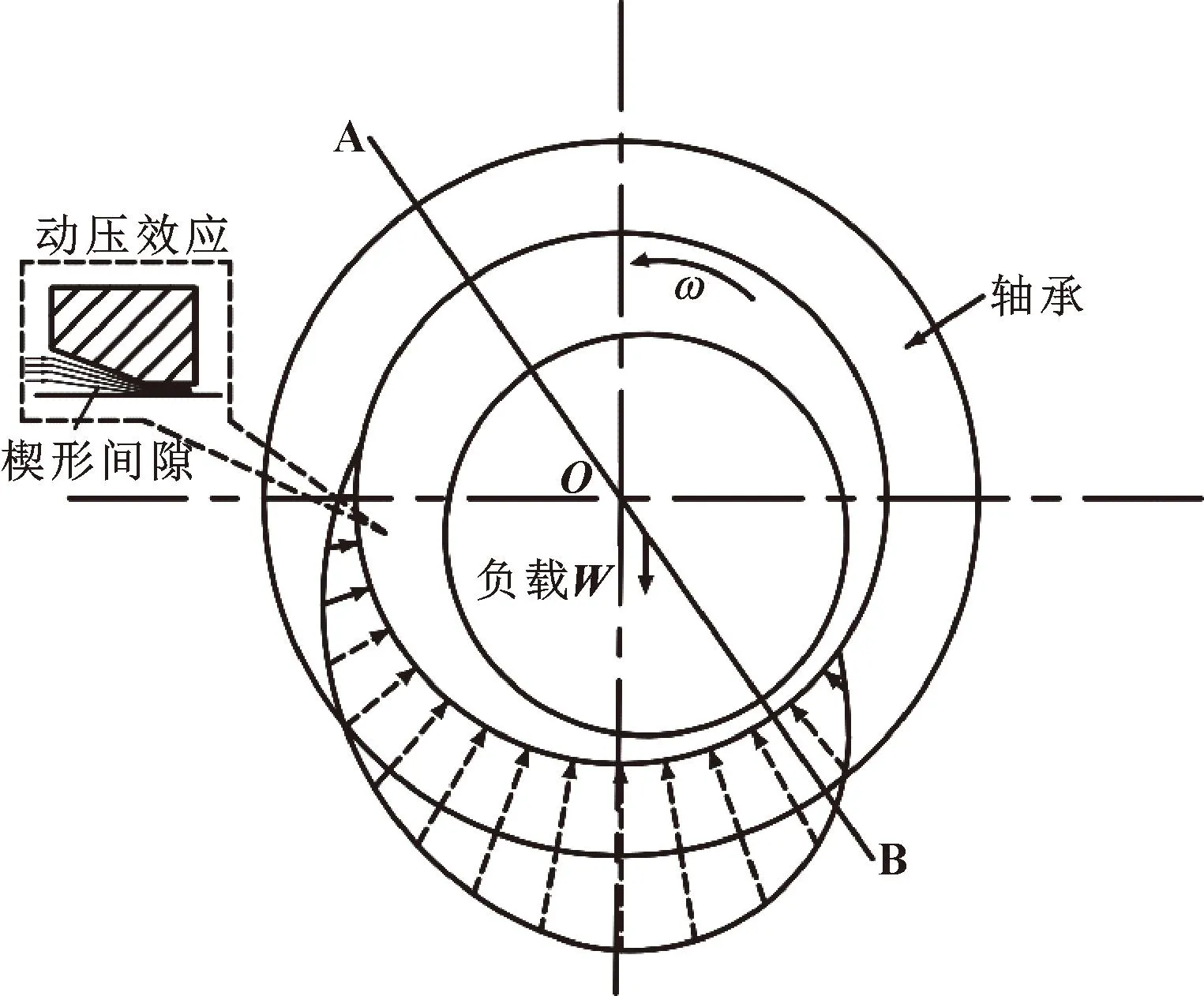
图2 径向螺旋槽空气轴承工作原理示意

试验轴承材料采用42CrMo，表面均进行热处理以提高材料硬度，并可以防止氧化；同时在轴承面均匀研磨厚度为0.5 μm的MoS2，不仅可以起到抗氧化的作用，其抗磁性还可以防止转子由于高速旋转可能磁化带来的影响。由于空气轴承在启停时存在摩擦，经过表面处理后，可以有效减少启停过程中转子与轴承套产生的摩擦，从而降低摩擦损耗，延长轴承的寿命[16]。试验采用的螺旋槽径向空气轴承如图3所示。

图3 螺旋槽空气轴承

2 微分方程的推导及求解

对于在可变气膜厚度下运行的螺旋形凹槽气体润滑轴颈轴承周围的平滑“整体”压力分布，可以获得等温可压缩流量的微分方程[17]，如式(1)所示。

(1)

式中：R为轴承半径；(Mθ)r、(Mz)r、(Mθ)g、(Mz)g为脊区与槽区单位表面长度质量流量的局部分量；ρ为密度，kg/m3；α为槽占槽脊整体的比例；β为槽角；ω1为带槽部件的转速；ω3为整体转速；r、θ、z为圆柱坐标。

图4所示为螺旋槽质量流量连续性分析的控制体积，其中ξ、η为与旋转方向和槽方向对齐的坐标；hg、hr分别为凹槽区和脊区域的膜厚；ξn为第n对脊-槽对开始处ξ的值；ΔSξn、ΔSη为控制体积曲面。

图4 质量流量连续性分析的控制体积

对于气体轴承通常假设轴承间隙中的气体是等温的，在该假设下，质量通量可以通过压力p表示。结合局部质量通量与整体压力的关系式为

(2)

α6μ(U-V)(hg-hr)cosβsinβ]

(3)

(4)

hr)cosβsinβ]

(5)

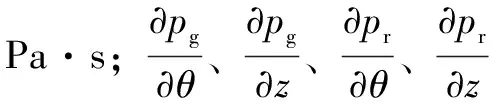
因此方程(1)—(5)构成了p1(θ*，z)的微分方程。

通过上述变换可以得到

(6)

对式(6)积分一次并应用边界条件

p0(z)=pa，z=0

(7)

得到p0(z)=

(8)

通过摄动分析，收集一阶项获得p1(θ*，z)的微分方程形式为

(9)

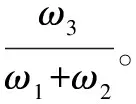
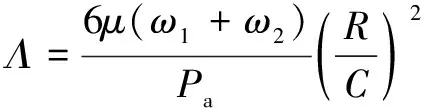
(10)

(11)

p1(θ*，z)必须满足的边界条件为

p1(θ*，z)=0，z=0

(12)

α(Mz)g+(1-α)(Mz)r=0，z=L/2

(13)

径向与切向承载力即为不同方向压力分布的二重积分。径向和切向承载力FR和FT、总承载力W及轴承姿态角φ由以下表达式计算：

(14)

(15)

φ=arctan(FT/FR)

(16)

(17)

当Wcosφ等于承载重量时，即为空气轴承的起飞速度，通过上述理论分析，可以得到：随着承载重量的增加，轴承的起飞速度也相应逐渐提高，但其承载质量存在一个临界值。表1即以最佳承载力为目标，代入量纲一参数后求解微分方程得出的螺旋槽空气轴承的结构参数。

表1 螺旋槽结构参数

3 试验装置设计与试验原理

设计组装的测试螺旋槽空气轴承起飞速度及高速承载能力的试验台及其原理图如图5所示[18]。包括：高速电机主轴(7.5 kW，24 000 r/min)、变频调速器、压力传感器、仪表显示器、电源适配器、铝板工作台、定制铝合金框架、砝码等。

图5 试验台照片及其原理

3.1 试验台结构

为了试验台稳定，将所有仪器固定在700 mm×400 mm×8 mm的铝板工作台上，主轴电机固定在铝板一端，转子通过夹头紧紧固定在电机上，使用千分仪测量其圆柱度，经多次调整后，使其圆柱度控制在误差1 μm范围内[19]。通过在轴承套(352 g)上固定力矩杆并放置在固定好的重力传感器上，重力传感器读数乘以力矩杆长度可以得到轴承摩擦力矩。变频器与电机连接，通过变频器可以驱动电机实现0～24 000 r/min的任意稳定转速输出。砝码通过固定在铝合金框架上的滑轮，可以控制轴承套的承载重量。

3.2 试验数据收集

试验数据包括：变频器示数、压力传感器示数、加载砝码记录。变频器示数单位为Hz，乘以60以后即为转子转速。

3.3 测试原理

起飞速度：通过重力传感器上的示数来判断螺旋槽空气轴承是否形成气膜。其原理为：在空气轴承达到起飞速度之前，转子与轴承套之间的摩擦为干摩擦，随着转速的升高，摩擦力矩逐渐增大，即重力传感器示数与力矩杆的乘积(T=F×L)增大；由于空气轴承及螺旋槽的动压效应，当气膜形成时，重力传感器示数会突然减小，最终稳定在一定数值；重力传感器最大值时的转速即为空气轴承的起飞速度。

通过滑轮不断调整加在轴承套上的载荷，读取重力传感器与变频器示数，来测试不同载荷下螺旋槽空气轴承的起飞速度。

4 试验结果与分析

4.1 螺旋槽空气轴承起飞速度

空载状态时，空气轴承起飞的条件为：气膜的承载力可以支撑轴承套本身的自重。

试验得到的轴承空载时，转速与摩擦力矩随时间的变化曲线如图6所示。

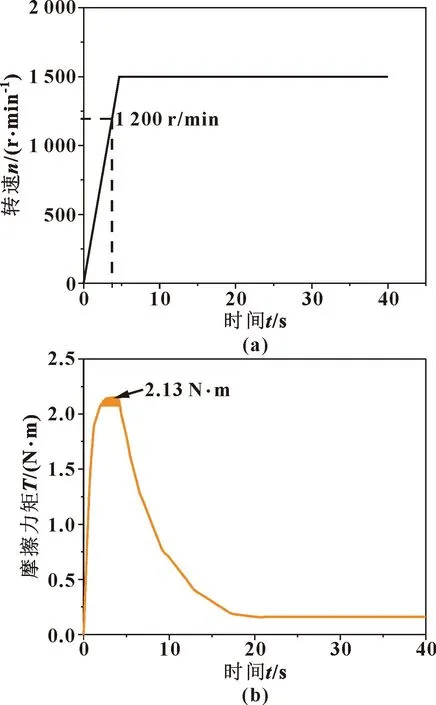
图6 转速(a)与摩擦力矩(b)随时间的变化

由图6可以看出，当电机启动以后，随着转速升高，摩擦力矩也近似线性增大，启动3.75 s后摩擦力矩达到最大值2.13 N·m，摩擦力矩最大值时的转速在1 200 r/min附近，即螺旋槽空气轴承空载时的起飞速度为1 200 r/min。

4.2 起飞速度与承载试验

轴承的承载能力是体现空气轴承性能的重要参数。它与轴承和轴颈的设计结构、槽参数、尺寸、材料和表面处理等密切相关[15]。试验所用电机最高转速可达24 000 r/min，文中在不同承载条件下测试了经过表面处理的空气轴承的起飞速度，并与理论计算的轴承起飞速度相比较，来验证测试结果的准确性。

试验开始转子保持2 000 r/min，轴承从空载开始逐渐加载，然后逐渐卸载，每次加载或卸载载荷为40 N(4 kg砝码)。为了保护电机，转速增加至20 000 r/min不再继续测试，分别测得负载为40、80、120、160 N及起飞速度到达20 000 r/min时所对应的负载，如图7所示。试验结果表明，随着负载的增加，空气轴承的起飞速度也逐渐增加，这与理论计算得出的规律相一致。在理论计算中，空气轴承起飞速度随着载荷的增加而升高，转速越高承载能力也逐渐提高，但是承载能力到达一定程度后便不再增加。由于试验电机达不到理论设计的60 000 r/min的转速，所以在转速增加至20 000 r/min过程中测试出的轴承承载能力一直在增加。与理论计算结果相比较，实际测试的不同载荷下的起飞速度要高出20%～30%。这可能是因温度等变化引起的，但起飞速度的变化趋势与理论计算相一致，证明了实验结果的正确性。

图7 起飞速度与摩擦力矩随载荷的变化

图8所示为轴承套试验后的磨损情况。可以看出，经过表面处理的空气轴承试验后磨损轻微，甚至可以承受十万次以上的启停试验。

图8 试验后轴承套磨损情况

5 结论

(1)搭建了径向螺旋槽空气轴承起飞速度与承载能力测试试验台，完成了试验轴承起飞速度与承载力的测试。结果表明，螺旋槽空气轴承的起飞速度随着载荷的增加而升高，起飞时的摩擦力矩随着载荷的增加而增大，起飞时的转矩随着载荷的增加而增大；随着转速的升高，螺旋槽空气轴承的承载能力也越来越大。

(2)试验轴承运转良好，证明了设计理论的正确，为后续径向螺旋槽动压空气轴承在不同载荷下的设计提供了理论支承。

(3)设计的轴承起飞速度与承载力试验结果虽低于理论计算结果，但试验结果证明了其性能依然可以满足很多应用场合的需要。