带人字槽和轴向微通槽的动静压气体轴承静态特性
2024-04-17李树森马添潇穆岩璞
李树森,马添潇,穆岩璞
(东北林业大学机电工程学院,黑龙江哈尔滨 150040)
超精轴承作为影响超精密加工的核心因素,对提升制造业水平具有举足轻重的作用[1]。在各种超精轴承中,动静压气体轴承相比静压气体轴承和动压气体轴承有着承载特性好和稳定性较优等优点,为此学者们对其进行了深入研究。李树森等[2]以人字槽小孔节流动静压气体轴承为研究对象,对气体轴承的气膜流场特性和承载特性进行了分析。王欣崎等[3]以螺旋槽小孔节流动静压气体轴承为研究对象,研究槽深、槽宽等参数对静态特性的影响。于贺春等[4]分析了人字槽狭缝节流动静压混合气体轴承,并通过仿真优化了该轴承设计参数。李树森等[5]以小孔节流深浅腔动静压气体轴承为研究对象,采用Fluent软件对轴承的承载特性进行分析。贾晨辉等[6]以球面螺旋槽动静压气体轴承为研究对象,研究了瞬态刚度和阻尼的震动特征。王广洲等[7]以人字槽狭缝节流气体轴承为研究对象,对其静态特性进行了研究。汲腾龙等[8]以狭缝节流动静压气体径向滑动轴承为对象,对其承载能力和稳定性进行了研究。
为了改进现有气体轴承刚度和承载能力不足的缺点,本文作者设计了一种新型带人字槽和轴向微通槽的动静压气体轴承,利用Fluent分析气体轴承的承载特性,研究轴向微通槽深度、偏心率、气膜厚度、供气压力对气体轴承承载能力和刚度的影响规律。
1 带人字槽和轴向微通槽动静压气体轴承的设计
动静压气体轴承的工作原理是动压气体轴承和静压气体轴承工作原理的混合叠加,使轴承在启停阶段因气体润滑产生静压承载,在主轴高速旋转时因气体的动压效应产生动压承载,进一步提升整个轴承的承载能力[9]。
为进一步提升气体轴承刚度和承载能力,设计了带人字槽和轴向微通槽的动静压气体轴承的结构,如图1所示。人字槽可以使动静压气体轴承产生动压效应以提升承载能力,轴向微通槽可以使压力均化,避免由小孔节流产生气锤自激的振动现象。
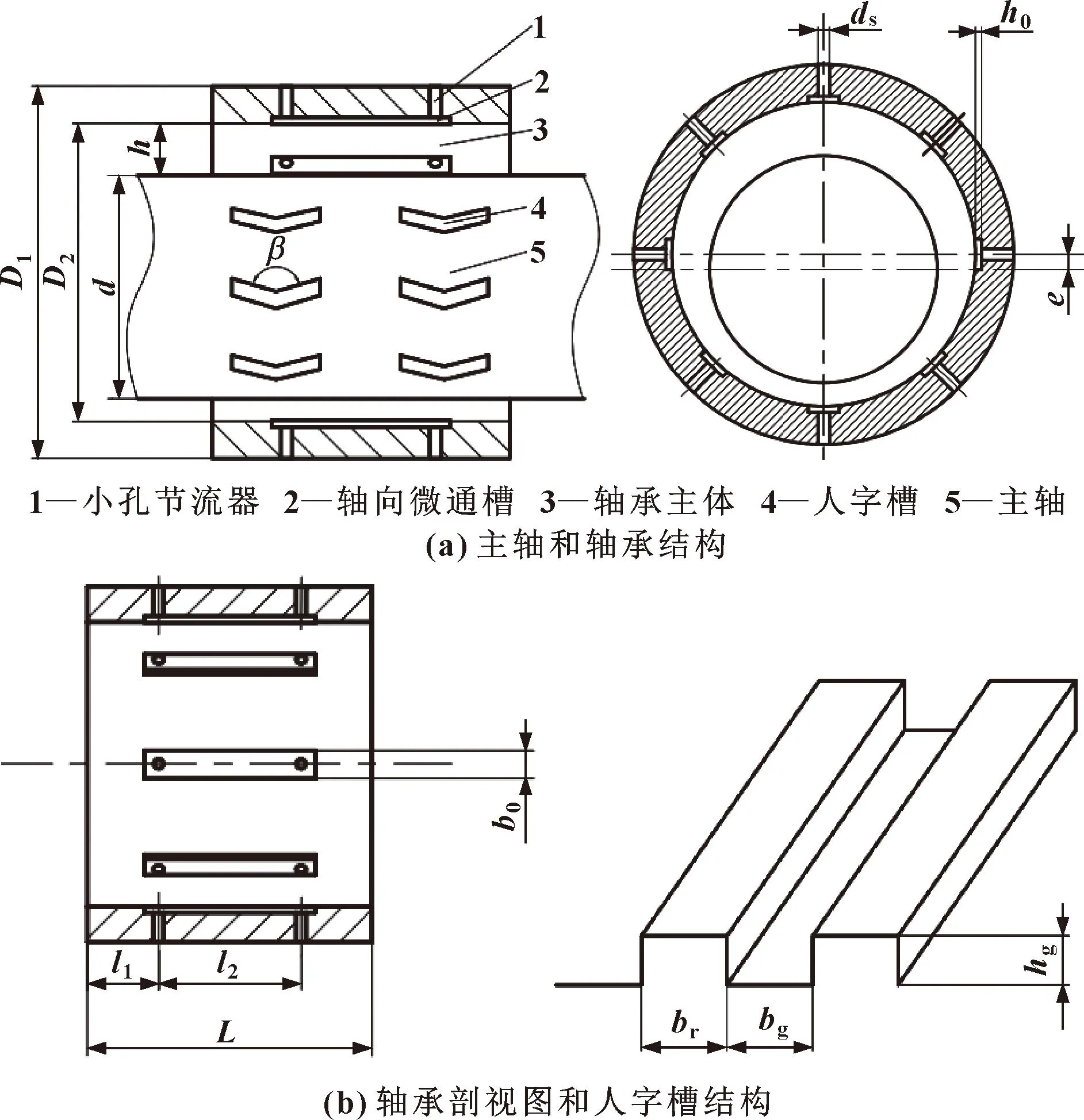
图1 带人字槽和轴向微通槽动静压气体轴承结构示意
设计的轴承上具有小孔节流器,并在小孔节流器之间开设轴向微通槽。主轴上开设双排人字槽,每排10个。同时主轴上开设双排供气孔,每排8个。轴向微通槽沿轴承内侧圆周方向均匀开设,共开设有8个,用以连接同一轴线上不同的两排小孔节流器出气口。
图1中,D1为轴承外径,D2为轴承内径,L为轴承长度,d为主轴直径,h为气膜厚度,β为人字槽槽角,ds为节流孔直径,h0为轴向微通槽深度,b0为轴向微通槽宽度,l1为孔边距,l2为孔距,hg为人字槽深度,bg为人字槽槽宽,br为人字槽槽台宽。初步确定主轴和轴承的结构参数和工作参数如表1所示。

表1 轴承的结构参数和工作参数
2 静态特性理论分析及仿真模型建立
2.1 带人字槽和轴向微通槽动静压气体轴承静态特性分析
利用有限元分析法求解雷诺方程,对带人字槽轴向微通槽的动静压气体轴承进行静态特性分析。
假设气体为理想气体,黏性系数为常数,气体流动为等温过程,考虑气体的可压缩性,气体在气膜间隙中不存在相对滑动。基于上述假设推导的雷诺方程如式(1)[10-13]所示。
(1)
式中:p为压力函数;ρ为流体密度;μ为气体动力黏度;vx、vz为气流速度分量。
引入量纲一化参数,取p0、hm、L为参考量,可得量纲一化雷诺方程如式(2)所示。
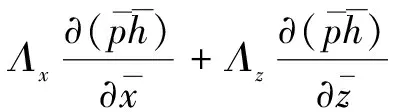
(2)
将狄利克雷函数δi引入,得到简化后的雷诺方程式(3)。
(3)
动静压气体轴承的承载力为气体轴承在静压阶段的承载力和气体轴承在外部气源停止供气后轴承高速稳定工作时的承载力相互耦合所得出,只需分别求出气体轴承在静压和动压工作状态下的承载力,就可求得动静压气体轴承的承载力,如式(4)所示。
W=Ws+Wd
(4)
计算静压阶段的承载力时,利用有限元分析的方法将气膜分割成n个单元体,并分别求解每个单元体的承载力Wλ,然后对所有单元体的承载力耦合从而求得轴承在静压阶段的总承载力Ws,如式(5)所示。
(5)
人字槽动静压气体轴承在动压阶段的承载力Wd按文献[14]中公式,如式(6)所示。
(6)
动静压气体轴承的刚度K可由承载能力的变化量和气膜厚度变化量得出,如式(7)所示。
(7)
2.2 建立仿真模型
利用Gambit软件对轴承的气膜模型进行网格划分。四面体网格在自动化、效率、可靠性以及几何通用性上要强于六面体网格,利用2阶的四面体进行网格划分可保证有限元分析的整体精度。由于气体轴承在空间3个方向的尺寸大小相差较大,气膜厚度一般在几十微米范围内,在网格生成时为了减小网格负体积出现的概率,文中使用了分块结构化网格的划分方法,划分结果如图2(a)所示。网格无关性验证如图2(b)所示。可见,当节点数达到50万后,计算的承载力不再变化,为了提高数值计算精度和控制计算时间,下文采用节点数50万进行计算。

图2 气膜模型网格划分及网格无关性验证
2.3 假设条件及边界条件的设定
假设条件设定:(1)在理论建模时,忽略润滑气体的惯性力和体积力对气膜的影响;(2)将润滑气体视为不可压缩气体,在润滑过程中气体连续、定常且整个润滑过程与外部无热能交换,为绝热过程;(3)将润滑气体视为牛顿流体;(4)假设润滑气体在流动时为层流状态。
模型采用压力进出口边界和壁面边界,16个进气口设置压力为ps=0.4 MPa,出口边界压力设为pa=0.102 MPa;主轴转速n=1×104r/min;偏心率设置为0.5;壁面为移动边界,方向设置为旋转;流体介质为理想气体并为常温流动,湍流模型采用k-εSST模型[15],并且开启曲率矫正从而保证边界层的梯度精度。
3 仿真结果与分析
3.1 供气压力对静态特性的影响
固定其他参数,分别选取供气压力为0.4、0.5、0.6、0.7、0.8 MPa,分析偏心率的变化对轴承刚度及承载能力的影响规律,结果如图3所示。
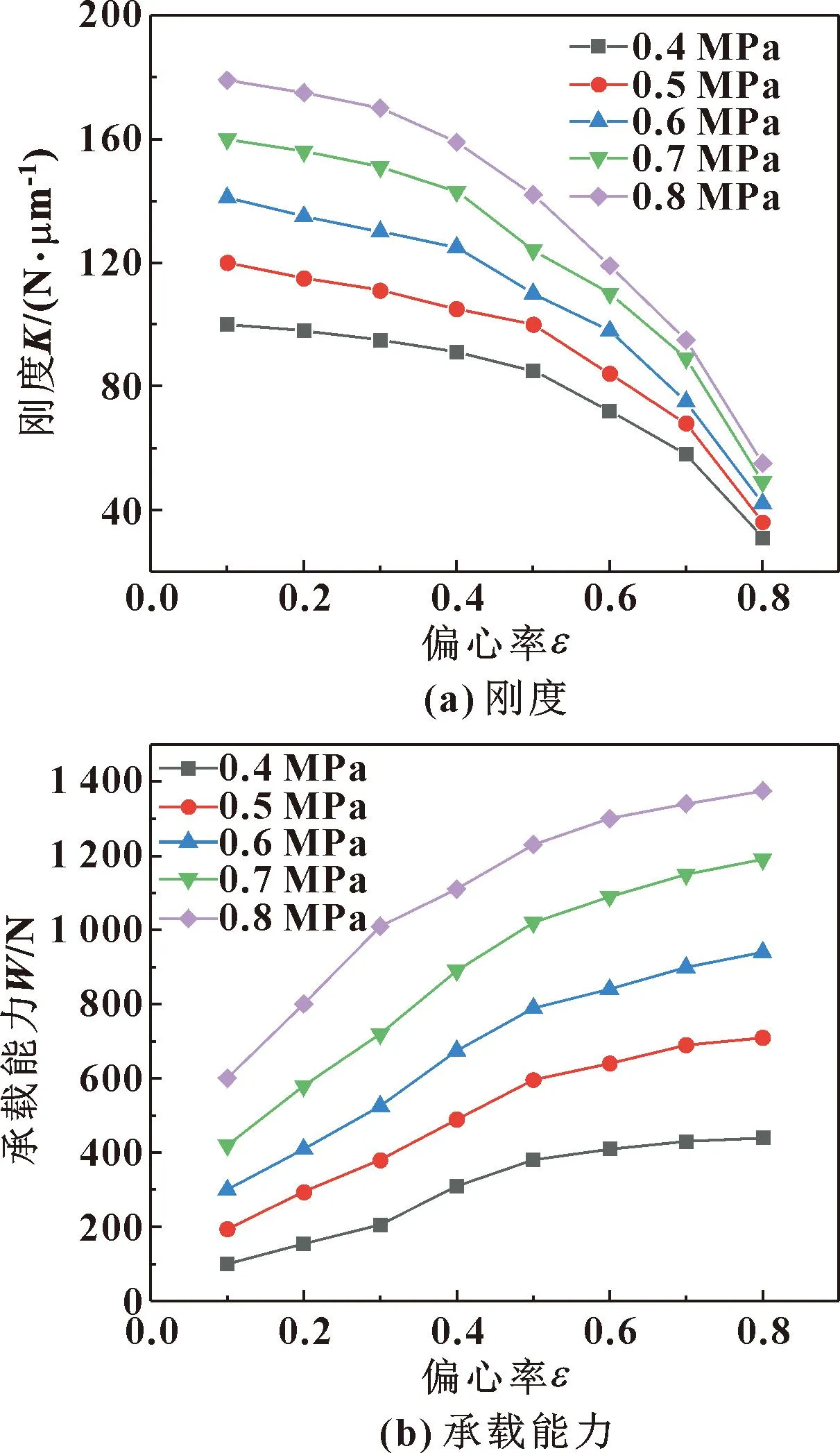
图3 不同供气压力下轴承刚度和承载力随偏心率的变化
由图3可知,在偏心率固定不变的情况下动静压气体轴承的刚度和承载能力随供气压力增大而增大,这主要是因为供气压力增大引起气膜压力增大;在相同供气压力下,随着偏心率增大,轴承的刚度不断减小,在偏心率从0.1到0.4增大时,轴承刚度减小的速度较为缓慢,在偏心率从0.4到0.8增大时,轴承刚度减小的速度不断增加;在相同供气压力下,随着偏心率的增大,动静压气体轴承的承载能力不断增大,偏心率从0.1到0.6增大时,轴承的承载能力增大速度较快,偏心率从0.6到0.8增大时,轴承的承载能力增大缓慢。由上述结果可知,当动静压气体轴承的偏心率过大时无法保证气体轴承的刚度要求,偏心率过小则无法保证承载能力的要求,设计气体轴承时应选择合适的偏心率,以同时满足轴承的承载能力和刚度的要求。
3.2 不同参数下人字槽对静态特性的影响
固定其他参数,在不同转速、偏心率、供气压力和气膜厚度下对比研究了有、无人字槽时气体轴承的刚度和承载能力变化规律,结果如图4—7所示。

图4 有、无人字槽气体轴承的刚度和承载能力随主轴转速的变化
由图4可以看出,在同一主轴转速条件下,相较不带人字槽的气体轴承,带人字槽的气体轴承的承载能力和刚度都显著提高,且随着主轴转速不断提升,二者的差距不断增大,这主要是因为随着转速提升人字槽产生的动压效应不断增强。由图5—7可知,带人字槽的气体轴承承载能力和刚度均高于不带人字槽的气体轴承,这主要是因为在主轴高速转动时,人字槽可以产生压力升,从而增大动静压气体轴承的刚度和承载能力。

图5 有、无人字槽时气体轴承的刚度和承载能力随偏心率的变化

图6 有、无人字槽时气体轴承的刚度和承载能力随供气能力的变化
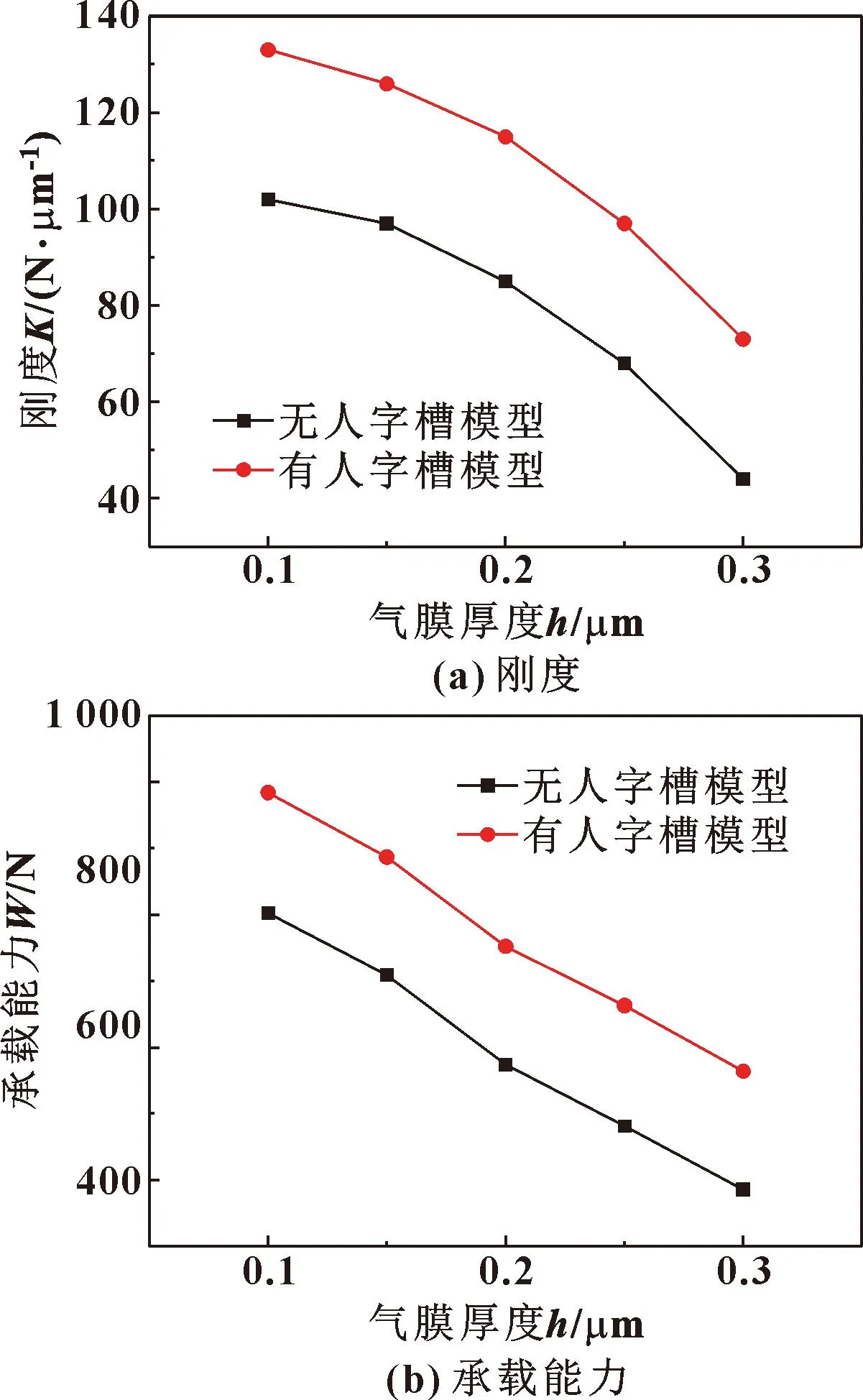
图7 有、无人字槽时气体轴承的刚度和承载能力随气膜厚度的变化
3.3 轴向微通槽深度对静态特性的影响
由以往的研究可知,带轴向微通槽的动静压气体轴承在气膜厚度为15~25 μm的情况下具有较高的承载力和刚度[16],故选取气膜厚度分别为15、20、25 μm,固定其他参数,研究轴向微通槽深度对轴承的刚度及承载能力的影响规律,如图8所示。
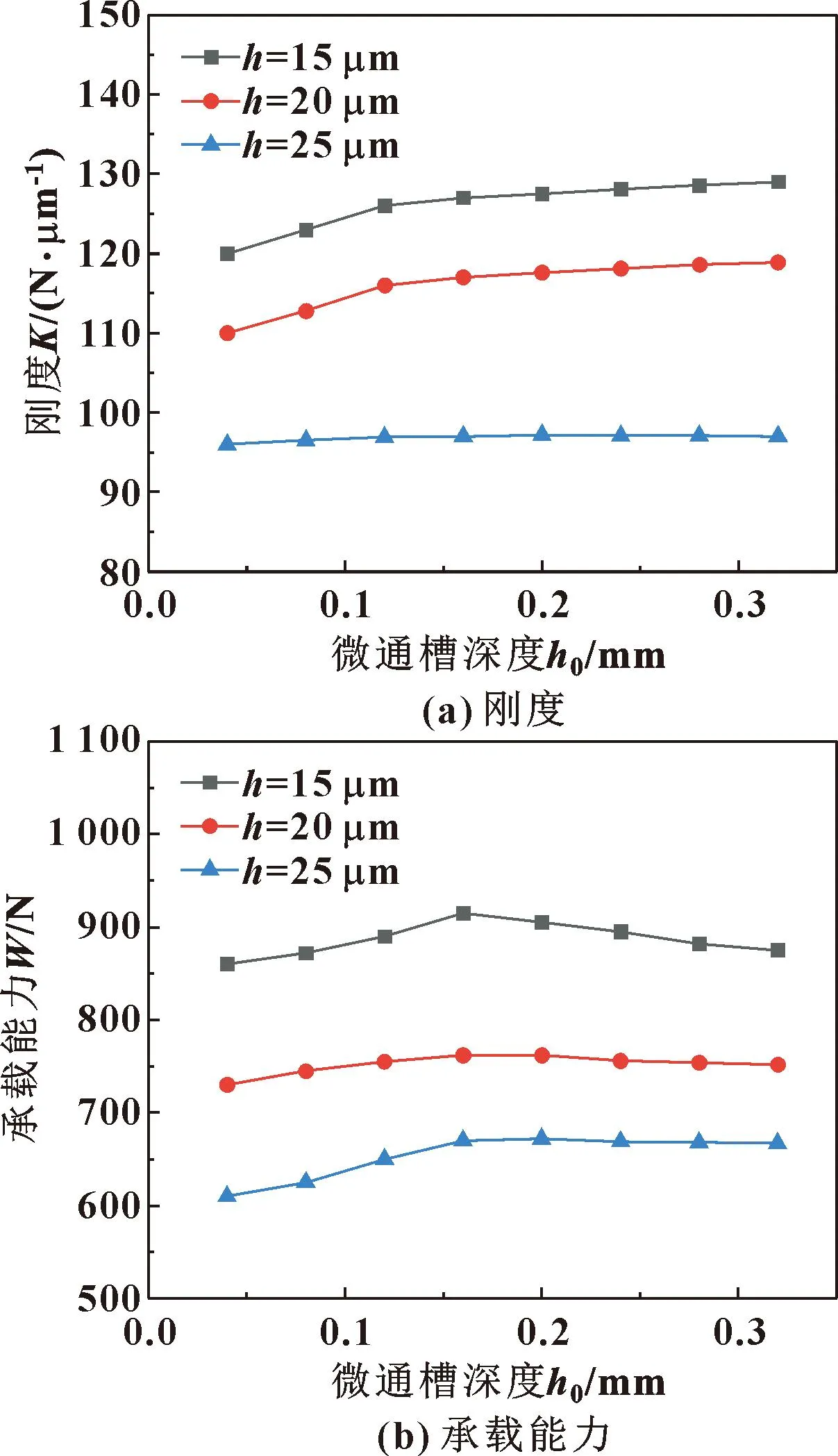
图8 不同气膜厚度下承载力和刚度随微通槽深度的变化
由图8可以看出,在同一微通槽深度下,轴承刚度和承载能力随着气膜厚度增大而减小;轴承刚度随着微通槽深度不断增大而增大,但在微通槽深度达到0.2 mm以后轴承的刚度提升变得十分不明显;轴承承载能力随着微通槽深度增大先增大,但当微通槽深度达到0.2 mm以后轴承的承载能力出现下降的趋势。上述结果表明,当气膜厚度为15、20、25 μm时,选用微通槽深度为0.16~0.2 mm的轴向微通槽,气体轴承的静态特性最佳。
3.4 仿真方法可靠性验证
利用MatLab软件对式(1)进行理论求解,得到带人字槽和轴向微通槽的动静压气体轴承在偏心率为0.5时轴承承载能力随转速的变化曲线,如图9所示。可见,理论计算结果与文中仿真结果基本一致,从而验证仿真方法的可靠性。理论曲线与仿真曲线有细小偏差主要是由于四面体网格精度有限,造成仿真结果与理论值有一定差异。
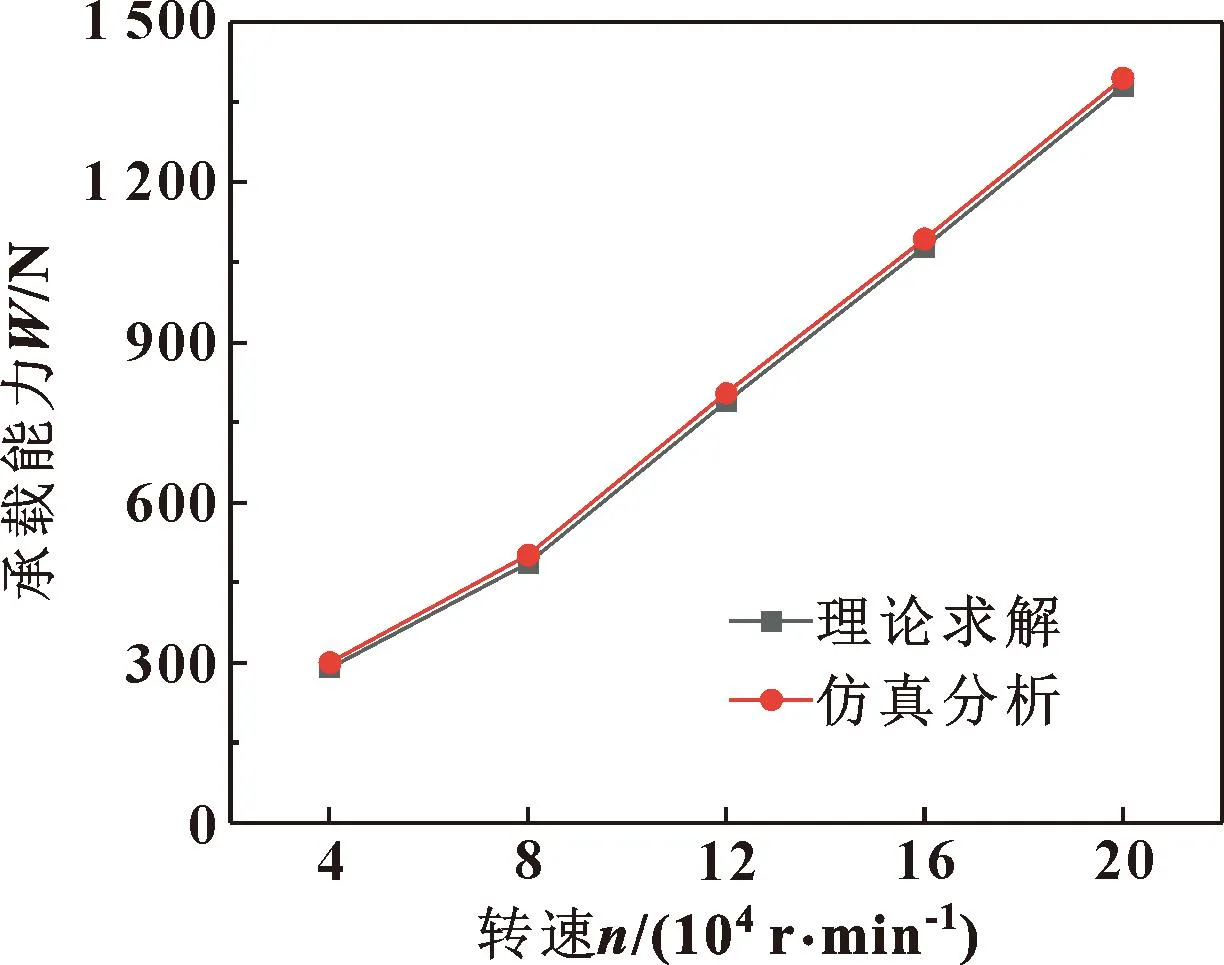
图9 理论求解与仿真分析结果对比
4 结论
对设计的带人字槽和轴向微通槽的动静压气体轴承静态特性进行仿真分析,研究不同结构参数和工作参数对轴承静态特性的影响规律,结论如下:
(1)偏心率保持不变的情况下,随着供气压力的升高,气体轴承的承载能力和刚度同时增大;随着偏心率增大,轴承刚度减小,承载能力增大。
(2)开设人字槽可以产生动压效应提升轴承的承载能力,主轴转速提高可以使动压效应增强从而改善气体轴承的承载能力和刚度。
(3)增大微通槽深度对提升气体轴承的刚度和承载能力有一定帮助,但当微通槽深度过大时,轴承承载能力会减小。
