基于瞬态有限元的齿轮箱迷宫密封泄漏研究

陈子昂，范静园，沈龙江，胡玉梅，杨光程

(1.重庆大学机械与运载工程学院，重庆 400030；2.中车株洲电力机车有限公司，湖南株洲 412001)

在齿轮箱动力及运动输入-输出的结构处，旋转轴与轴承座孔附近静止的箱体之间必须要留出间隙，否则运动件与静止件之间就会出现干涉，导致振动、磨损等[1]。然而，轴承及齿轮等滚滑界面必须要有润滑油进行润滑。例如高速列车齿轮箱采用飞溅润滑的方式对箱体内的齿轮、轴承等零部件进行润滑，箱体内大的油滴会被高线速度齿轮打碎成可以混入空气中的油雾，进而在压差的作用下进入到旋转轴与箱体轴孔之间的配合间隙处，随后在间隙中向外运动并最终进入大气，造成润滑油泄漏问题。

高速列车齿轮箱常采用非接触的迷宫密封来防止润滑油泄漏。迷宫密封可分为轴向迷宫密封和径向迷宫密封，它具有结构简单、使用寿命长、使用简单等特点，被广泛应用于齿轮箱动-静密封处[2]。迷宫密封通过节流间隙将压力能转化为动能，再通过空腔的涡流效应将流体的动能耗散，以此来达到密封的效果[3-4]。

但是，迷宫密封结构不尽相同，当结构参数设计不当，润滑油仍会有较多泄漏[5]。为此，国内外学者做了大量研究。张雨等人[6]研究了空腔宽度对直通式迷宫性能的影响，发现随着空腔宽度的增加，润滑油泄漏量减少。巴鹏等人[7-8]研究了空腔深度、密封间隙对迷宫密封性能的影响，发现迷宫密封泄漏量随空腔深度的增加而减少，随着间隙宽度的增大而逐渐增大。夏威等人[9]研究了齿高对密封性能的影响，发现油气泄漏率随齿高的增加呈先降低后增加的趋势。汤赫男等[10]研究了齿形角对迷宫密封性能的影响，发现随齿形角的增大，迷宫密封的泄漏量呈先减小后增大的趋势，当齿形角为30°时，迷宫密封性能最佳。此外，STOFF[11]首次采用有限差分法对迷宫密封中不可压缩流体进行了计算；ZHAO等[12]分析了空腔对直通式轴向迷宫密封的影响；RHODE和NAIL[13]采用计算流体动力学软件探究了迷宫密封结构参数对泄漏量的影响。

这些研究说明迷宫密封结构的几何参数对密封性能的影响存在规律性，同时还与旋转的轴与静止的箱体孔配合处的转速差有关。另外考虑到箱体及齿轮传动系统的振动，旋转的轴与静止的箱体孔配合处的间隙不宜设计得过小[14]，通常情况下该间隙不会小于0.2 mm。对于具体的迷宫密封结构，需合理选择迷宫密封结构几何参数，才能确保在间隙不过小的情况下最大程度减少泄漏量。

某高速机车驱动齿轮箱的迷宫密封存在润滑油泄漏现象，经多次分析和调整仍没有解决问题。本文作者以该迷宫密封结构为研究对象，采用ANSA软件建立该齿轮箱及迷宫密封的有限元模型，并运用FLUENT软件对齿轮箱和迷宫密封的内部流场进行了数值模拟。首先，通过对齿轮箱内部流场进行仿真，得出密封口的压力值与油液体积分数，作为迷宫密封结构的入口边界条件。接着，分析了迷宫密封结构的相对啮合深度、节流齿厚、回油孔直径和个数、齿离台阶距离、齿宽、密封间隙对密封性能的影响。最后，对迷宫密封结构进行改进，改进后的迷宫密封结构润滑油泄漏量稳定时段的平均漏油量降为原始密封结构漏油量的3.6%。文中对迷宫密封的研究结果，可为工程实际中合理设计齿轮箱迷宫密封结构提供一定的参考。

1 驱动齿轮箱内部流场仿真分析

为了给后续迷宫密封内部流场仿真分析提供入口边界条件，需要先对高速列车的驱动齿轮箱进行内部流场仿真分析，得到迷宫入口处的压力和油液体积分数。相关的分析工作包括：利用ANSA软件对齿轮箱结构进行几何清理与网格划分，齿轮箱内部流场有限元模型建立与仿真分析等。

1.1 齿轮箱几何清理与内部流场有限元模型建立

所研究的齿轮箱由3个圆柱直齿轮及若干零部件装配而成。先利用ANSA软件对齿轮箱进行几何清理，得到齿轮箱的简化模型如图1所示；然后对齿轮箱进行网格划分，进而建立齿轮箱有限元模型如图2所示。

图1 齿轮箱简化模型

图2 齿轮箱有限元模型

1.2 边界条件

齿轮箱采用飞溅润滑方式进行润滑，润滑油密度取866 kg/m3，黏度取16.6 mm2/s，箱体内润滑油总量为8 L。齿轮箱内部流场仿真模型如图3所示，小齿轮为主动轮，转速为3 500 r/min；红色部分表示润滑油，绿色部分表示最高油液面，蓝色箭头表示齿轮的旋转方向。设置通气孔out1、out2、out3为压力出口，压力为标准大气压，设置密封口监测面S。

图3 齿轮箱内部流场仿真模型

1.3 仿真结果

采用1.2节的仿真条件，对驱动齿轮箱内部流场进行仿真。提取密封口S处绝对压力值和油液体积分数，绝对压力与时间的关系如图4所示，油液体积分数与时间的关系如图5所示，Tc为大齿轮旋转一周所用的时间。

图4 密封口S处压力变化曲线

图5 密封口S处油液体积分数变化曲线

由图4和图5可知，通过对高速列车驱动齿轮箱内部流场进行仿真分析，得出了密封口的绝对压力平均值为102 939 Pa，油液体积分数平均值为11%，为后续迷宫密封内部流场仿真分析提供了入口边界条件。

2 迷宫密封仿真方法可行性验证

为了确保文中迷宫密封仿真分析结果正确可靠，通过理论计算与仿真结果对比，来验证迷宫密封仿真方法的可行性，确保后续仿真分析的准确性。

2.1 迷宫密封泄漏量理论计算

图6所示为直通式迷宫密封结构，其几何参数如表1所示。在迷宫密封理论研究方面，高光藩和白凤娥[15]总结了迷宫密封泄漏速率的计算公式，并经过大量实验数据进行了验证。泄漏量理论公式如式(1)所示。

(1)

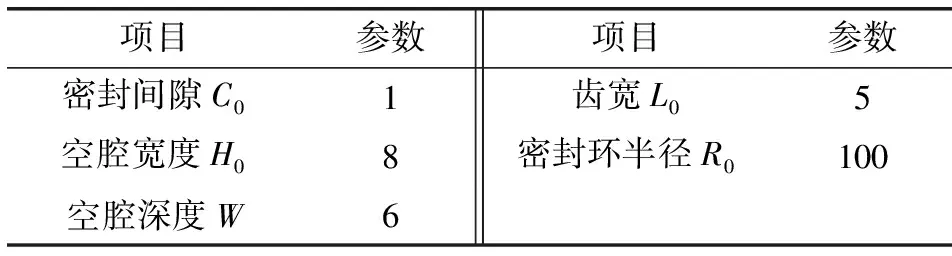
表1 直通式迷宫密封几何参数 单位：mm

图6 直通式迷宫密封结构

式中：G为泄漏量，kg/s；ψ为迷宫系数，取3.34；A1、An为前后节流间隙面积，A1=6.3×10-4m2，An=6.3×10-4m2；n为节流齿数；λ为迷宫总压力比，λ=pn/p0，p0、pn为密封前后流体介质的绝对压力，p0=103 325 Pa，pn=101 325 Pa；T0为流体介质初始温度，取298 K；R为气体常数，取2.1×103J/(kg·K)。计算得出直通式迷宫密封的泄漏量理论值为0.053 4 kg/s。

2.2 迷宫密封泄漏量仿真分析

运用FLUENT软件对图6所示直通式迷宫密封结构进行仿真，得到迷宫密封泄漏量与时间的关系曲线如图7所示，计算出口流量稳定时段的平均值为0.049 3 kg/s。

图7 迷宫密封结构出口流量曲线

2.3 理论与仿真对比

通过FLUENT软件模拟出的泄漏量为0.049 3 kg/s，理论计算的直通式迷宫密封泄漏量为0.053 4 kg/s，两者之间的误差仅为7.7%，证明了文中迷宫密封仿真方法的可行性。

3 原始迷宫密封结构泄漏仿真分析

某高速列车驱动齿轮箱润滑油泄漏严重，文中基于ANSA软件建立原始迷宫密封流场有限元模型，并运用FLUENT软件对其仿真分析，获取原始迷宫密封的润滑油泄漏量，为后续迷宫密封结构改进提供了参考。

3.1 驱动齿轮箱密封口S处迷宫密封结构

驱动齿轮箱密封口S处的迷宫密封结构如图8所示，图9给出了其轴向截面图。

图8 迷宫密封结构

由图9可知，该密封结构由径向迷宫密封和轴向迷宫密封组成。为了减少仿真时间成本，文中针对径向迷宫密封(见图10)和轴向迷宫密封(见图11)分别展开探究。其中T/L为相对啮合深度、H为齿厚、C1为径向间隙、C为密封间隙、B为齿宽、P为齿与台阶距离。原始迷宫密封结构参数如表2所示，其有限元模型网格划分方式如图12所示。

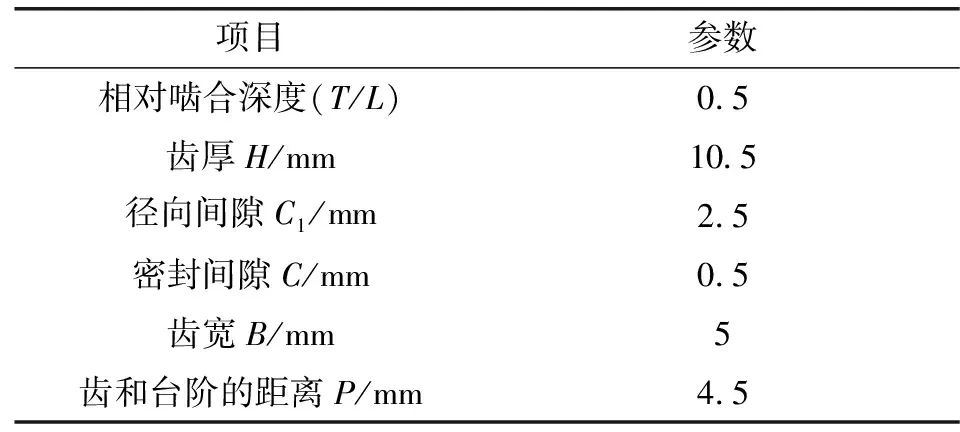
表2 原始迷宫密封结构参数

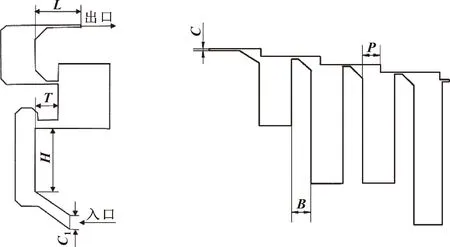
图10 径向迷宫密封

图12 迷宫密封有限元模型网格划分

3.2 边界条件

采用齿轮箱内部流场的仿真结果，设置入口边界条件为压力入口，绝对压力值为102 939 Pa，出口边界条件为压力出口，压力为标准大气压，即101 325 Pa。油液体积分数为11%，转子转速取1 410 r/min，空气介质采用理想气体。选用κ-ε湍流、Euler双相流模型，结构壁面采用无渗透、无滑移边界条件，且均按绝热面处理。为了保证仿真精度，有限体积法离散控制方程均采用二阶迎风格式离散，且采用分离求解方式；同时，为了缩短仿真时间，在迷宫密封内部流场中预设油液体积分数为11%的流体介质。

3.3 密封口S处迷宫密封仿真结果

采用3.2节的仿真边界条件，对原始迷宫密封结构进行仿真。提取油液速度矢量图和压力云图分别如图13、图14所示；迷宫密封结构润滑油泄漏量与时间的关系曲线如图15所示。

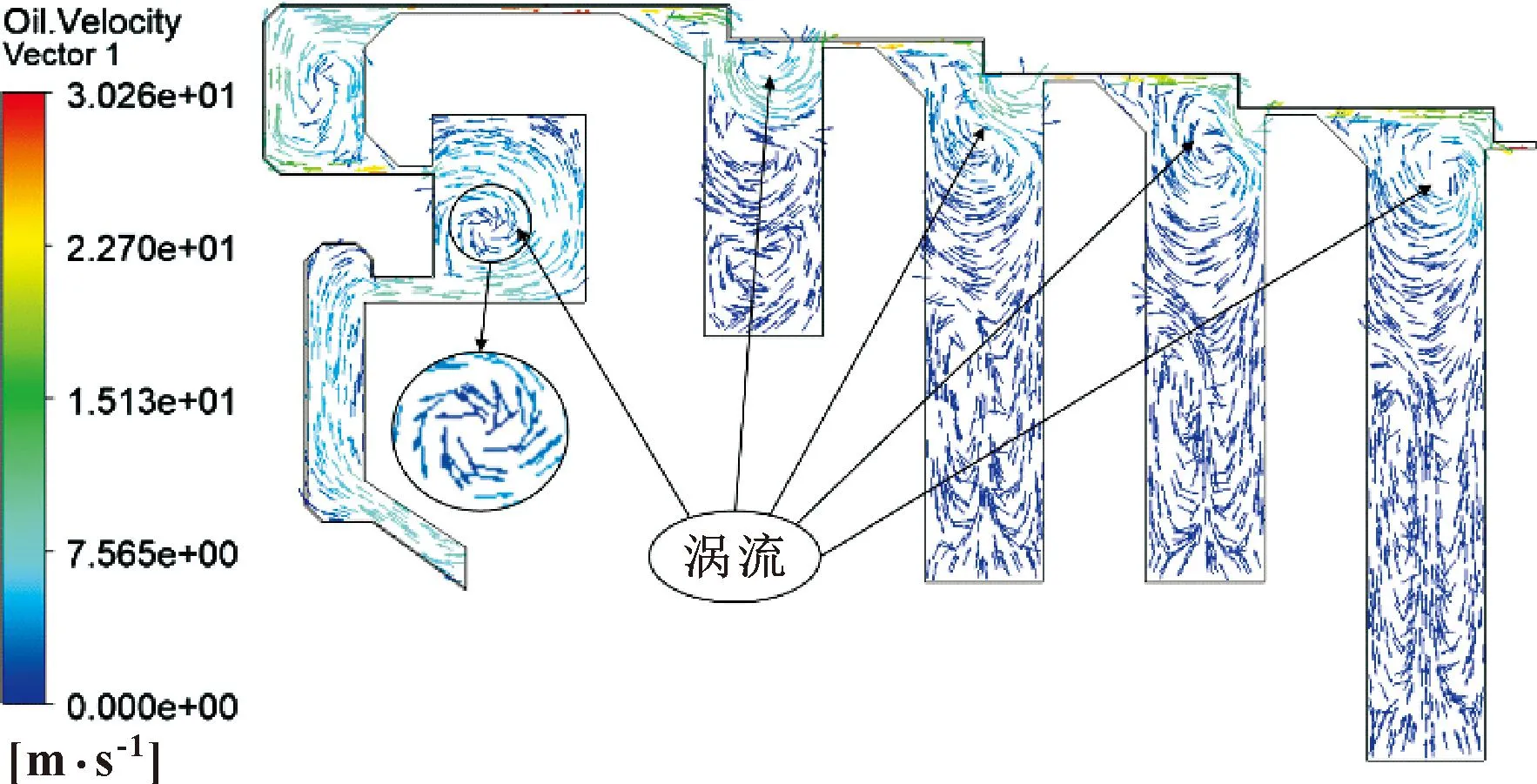
图13 原始迷宫密封结构油液速度矢量图

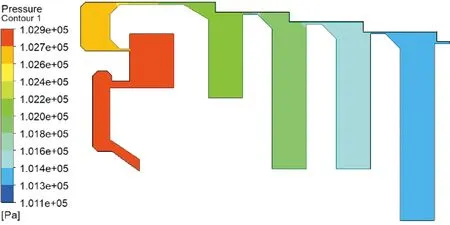
图14 原始迷宫密封结构压力云图

图15 原始迷宫结构润滑油泄漏量曲线

由图13、图14可知，从密封结构入口到出口，由于节流作用和空腔耗散作用，压力分布呈现逐渐降低的趋势。由图15计算仿真稳定时段的润滑油泄漏量平均值为0.025 1 kg/s，泄漏量较大，因此，需要对迷宫密封结构进行改进。

4 径向迷宫密封结构参数影响分析

为了探究迷宫密封结构参数对密封性能的影响规律，采用3.2节的仿真边界条件，对迷宫密封的内部流场进行仿真分析，研究了相对啮合深度、齿厚及径向间隙对径向迷宫密封性能的影响，分析了回油孔的直径及数量、齿与台阶距离、齿宽、密封间隙对轴向迷宫密封性能的影响，研究结果为之后迷宫密封的结构改进提供了参考。

4.1 相对啮合深度对径向迷宫密封性能的影响

迷宫密封模型采用3.2节的仿真条件，以原始模型相对啮合深度0.5为中间值，分别建立相对啮合深度为-0.1、0、0.5、0.7、0.9的5组模型，并对其进行仿真。图16给出了相对啮合深度分别为-0.1、0、0.5、0.9的油液速度矢量图，对各个模型的出口油液流量进行提取，得到迷宫密封结构相对啮合深度与润滑油泄漏量的关系如图17所示。

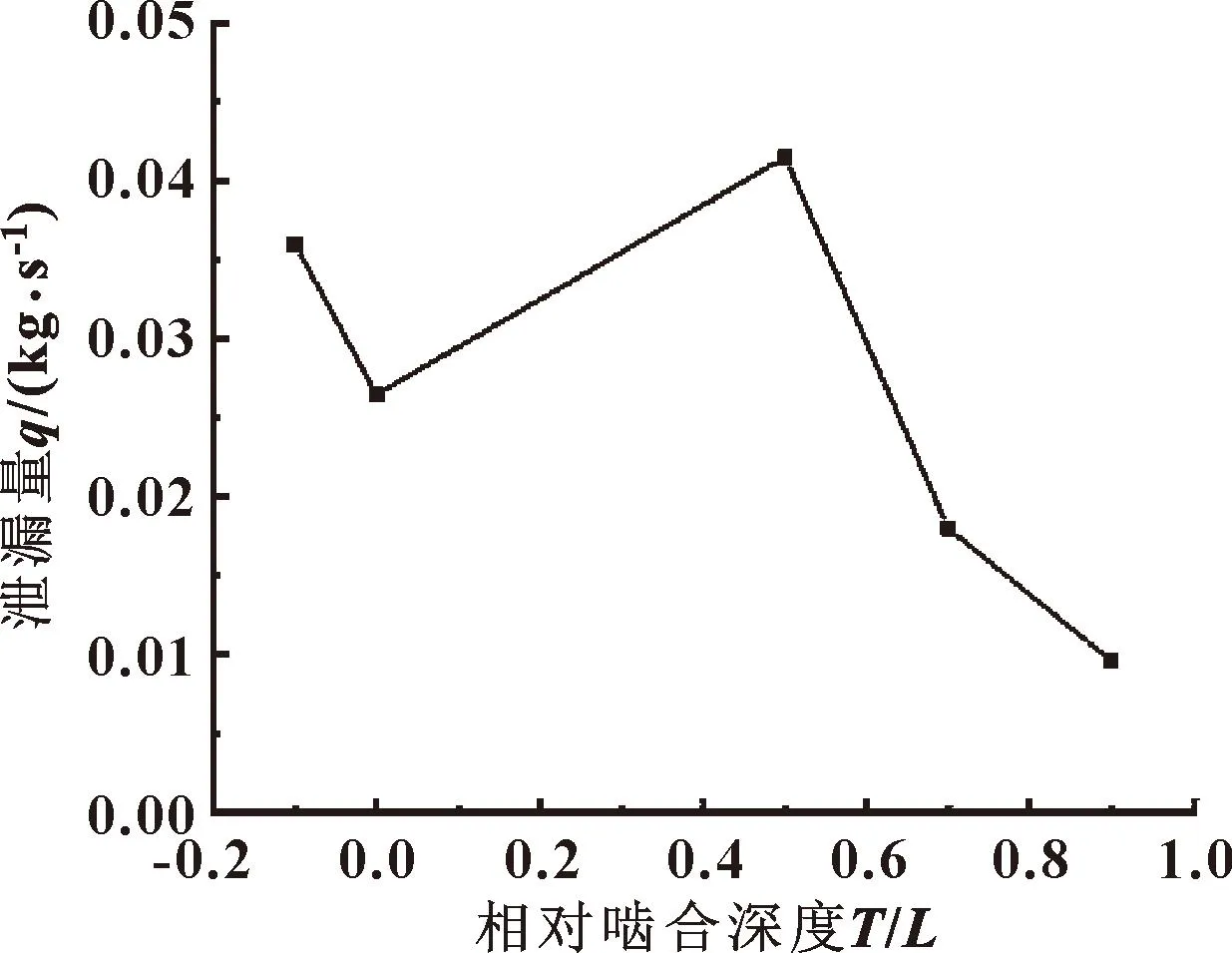
图17 相对啮合深度与润滑油泄漏量关系

如图16和图17所示，当相对啮合深度由-0.1向0变化时，由于节流齿缝隙和空腔出入口缝隙减小，增强了节流效应，润滑油泄漏量减少；当相对啮合深度由0向0.5变化时，空腔深度减小，进而减弱了空腔中涡流的动能耗散作用，润滑油泄漏量增加；当相对啮合深度由0.5向0.9变化时，空腔深度减小使涡流耗散作用继续减弱，但随着相对啮合深度的增加，节流齿缝隙继续减小，使得节流效应增强，润滑油泄漏量减少。

当相对啮合深度大于0.5时，随着相对啮合深度的增加，迷宫密封的泄漏量越来越少。综合考虑结构的可行性以及迷宫密封的性能，相对啮合深度0.7为最佳选择。

4.2 节流齿厚对径向迷宫密封性能的影响

迷宫密封模型采用3.2节的仿真条件，以原始模型节流齿厚10.5 mm为中间值，分别建立节流齿厚H为6.5、8.5、10.5、12.5、14.5 mm的5组模型，并对其进行仿真。图18给出了节流齿厚分别为6.5和14.5 mm的油液速度矢量图，节流齿厚和润滑油泄漏量之间的关系如图19所示。

图18 不同节流齿厚下油液速度矢量图

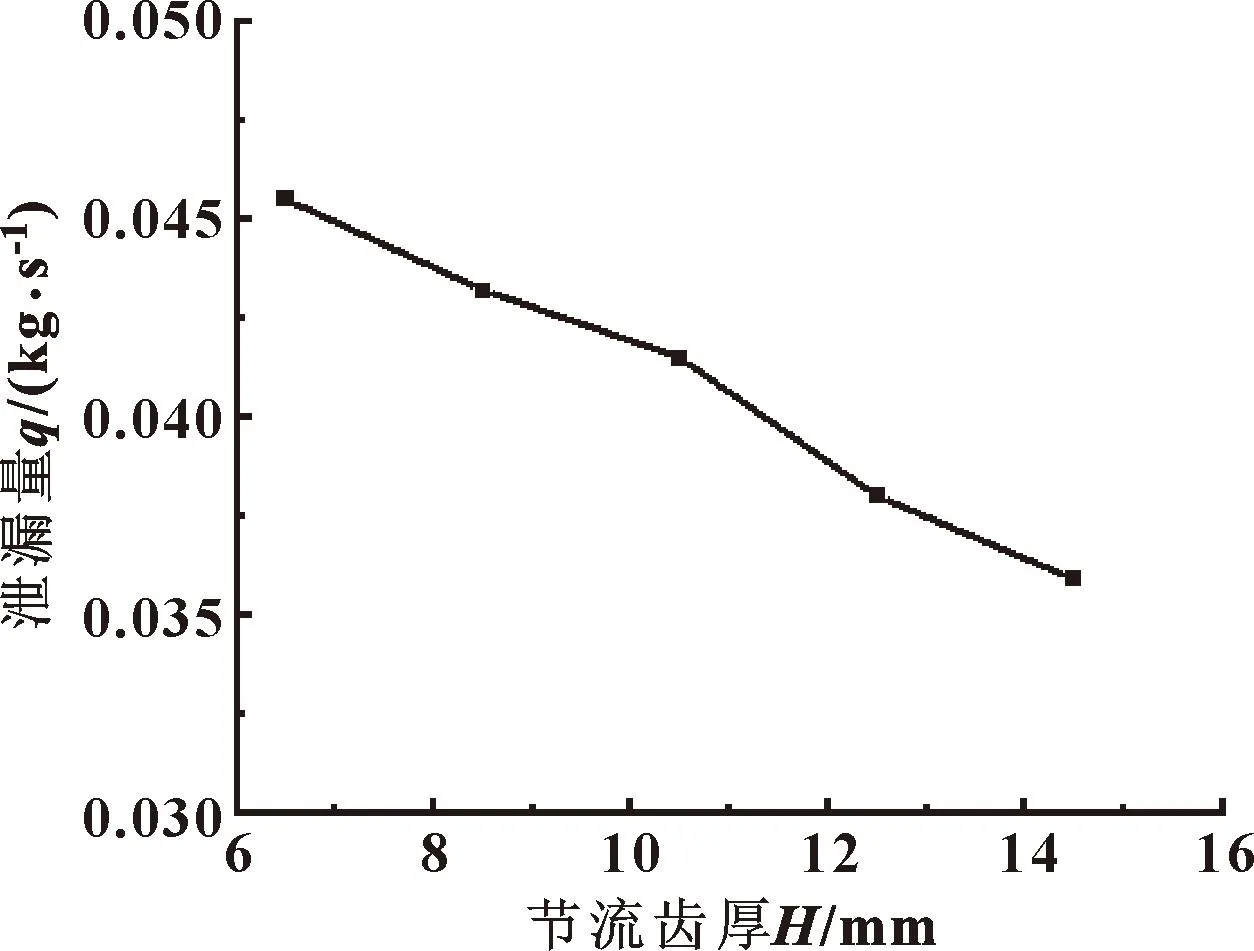
图19 节流齿厚与润滑油泄漏量关系

如图19所示，随着节流齿厚的增加，润滑油泄漏量呈下降趋势。增加节流齿厚加强了其节流效应，进而使润滑油泄漏量减少。为了最大程度提升密封性能，并兼顾结构限制，节流齿厚应选择14.5 mm。

4.3 径向间隙对径向迷宫密封性能的影响

迷宫密封模型采用3.2节的仿真条件，分别建立径向间隙C1为0.5、1、1.5、2、2.5 mm的5组模型，并对其进行仿真。图20给出了径向间隙分别为0.5和2.5 mm的油液速度矢量图，径向间隙和润滑油泄漏量之间的关系如图21所示。

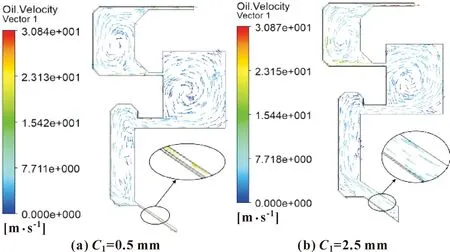
图20 不同径向间隙下油液速度矢量图

图21 径向间隙与润滑油泄漏量关系

如图21所示，随着径向间隙的增加，密封结构的泄漏量增加。径向间隙增加使得入口节流效应减弱，单位时间内进入密封结构的润滑油量增加，而节流齿的节流效应和空腔的涡流耗散作用有限，最终导致密封结构润滑油泄漏量增加。考虑到结构的限制，建议径向间隙取值0.3～0.5 mm。

5 轴向迷宫密封结构参数影响分析

5.1 回油孔直径的影响

大直径回油孔可以有效地将密封空腔底部的润滑油排出，但静子空腔的宽度有限，且过大的回油孔可能会增加空腔的透气效应，不利于空腔中涡流的形成，进而影响迷宫密封结构的性能。因此应在满足回油的条件下，尽可能地减小回油孔直径。在轴向迷宫密封结构每个空腔底部均设置一个回油孔，共4个回油孔。回油孔位置如图22所示。

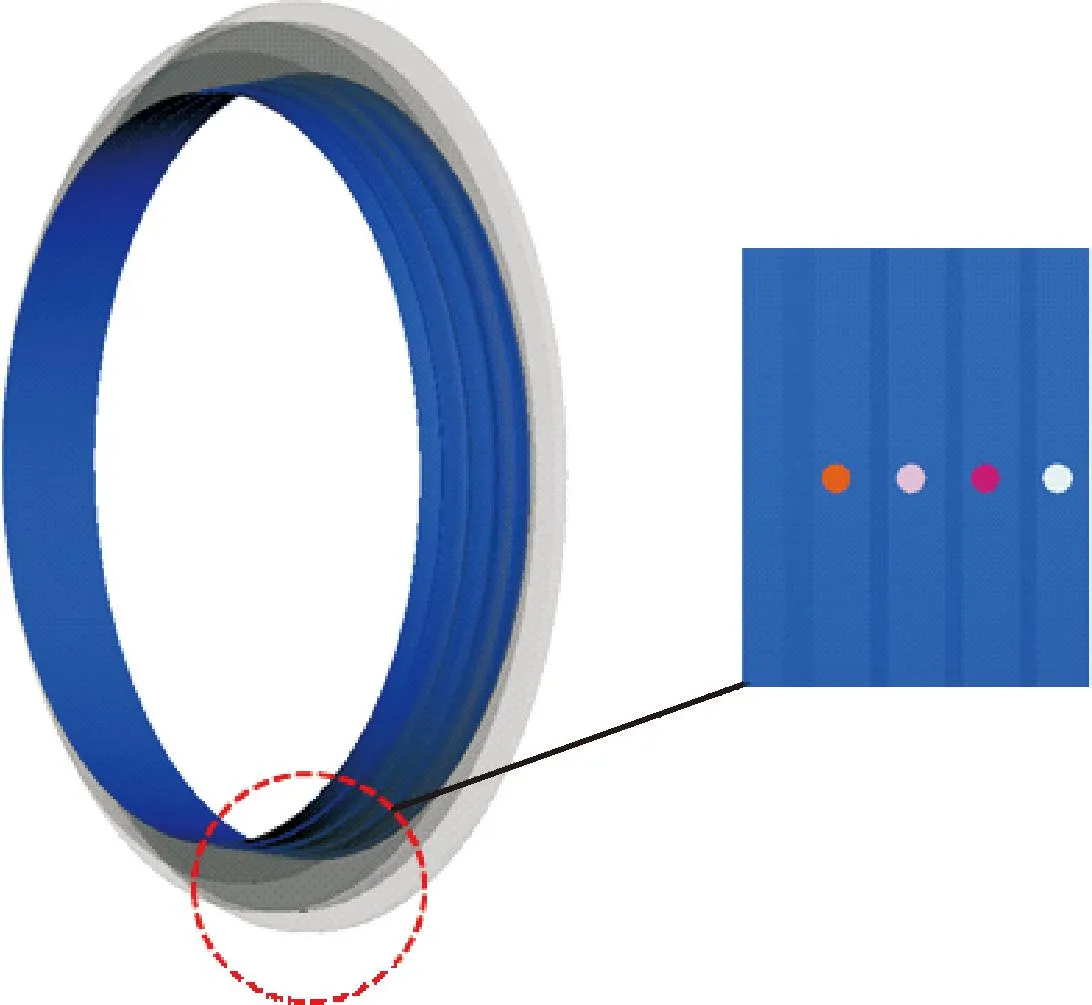
图22 回油孔位置

迷宫密封模型采用3.2节的仿真条件，分别建立回油孔直径为2、3、4、5、6 mm的5组模型，并对其进行仿真。图23给出了回油孔直径分别为2和6 mm的油液速度矢量图，回油孔直径和润滑油泄漏量的关系如图24所示。

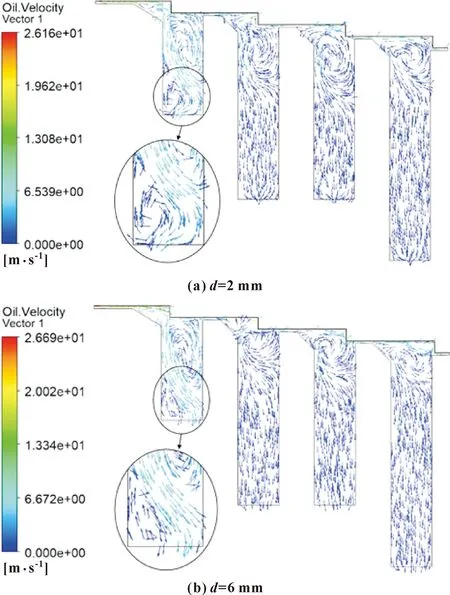
图23 不同回油孔直径下油液速度矢量图

图24 回油孔直径与润滑油泄漏量关系

如图23所示，第一个空腔内高流速油液分布区域最广，而其他3个空腔内油液流速偏低。这说明第一个空腔的回油孔承担着主要的回油作用。

如图24所示，随着回油孔直径的增加，润滑油的泄漏量呈下降趋势。这说明在研究范围内，回油孔的回油作用大于其对空腔涡流的破坏作用，进而使密封性能增强。当回油孔直径由5 mm向6 mm变化时，润滑油泄漏量变化率较低。考虑到所研究齿轮箱密封的具体结构限制，回油孔直径宜选用5 mm，如果结构允许，6 mm及以上更佳。

5.2 回油孔数量的影响

选用合适的回油孔数量对降低润滑油泄漏量至关重要。在轴向迷宫密封空腔底部建立回油孔数量分别为1、2、3、4、5的5组模型，回油孔直径均为5 mm，分布形式如图25所示。采用3.2节的仿真条件，对其进行仿真，得到回油孔数量和润滑油泄漏量的关系如图26所示。

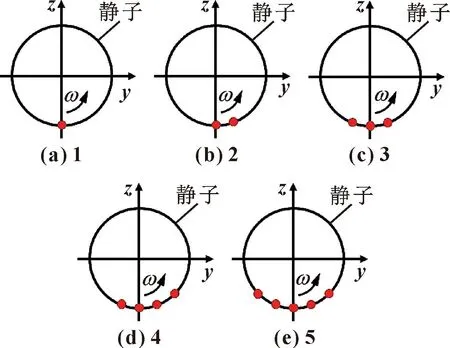
图25 各回油孔数量下孔的布置方式

图26 回油孔数量与润滑油泄漏量关系

如图26所示，轴向迷宫密封结构的泄漏量随着回油孔数量的增加而减少，但随着回油孔数量的增加，其对泄漏量的影响越来越小。综合考虑，回油孔数量宜选择4个。

5.3 齿与台阶距离对轴向迷宫密封性能的影响

如图27所示，原始密封结构中的各个齿离相应台阶的距离分别为1.5、3.5、5.5、7.5 mm，平均值为4.5 mm。将各尺寸等量变化，分别建立密封齿与台阶距离平均值为4、4.5、5、5.5、6 mm的5组模型，迷宫密封模型采用3.2节的仿真边界条件。

图27 轴向迷宫密封结构(mm)

图28给出了齿与台阶平均距离分别为4和6 mm的油液速度矢量图，齿与台阶距离与润滑油泄漏量的关系如图29所示。

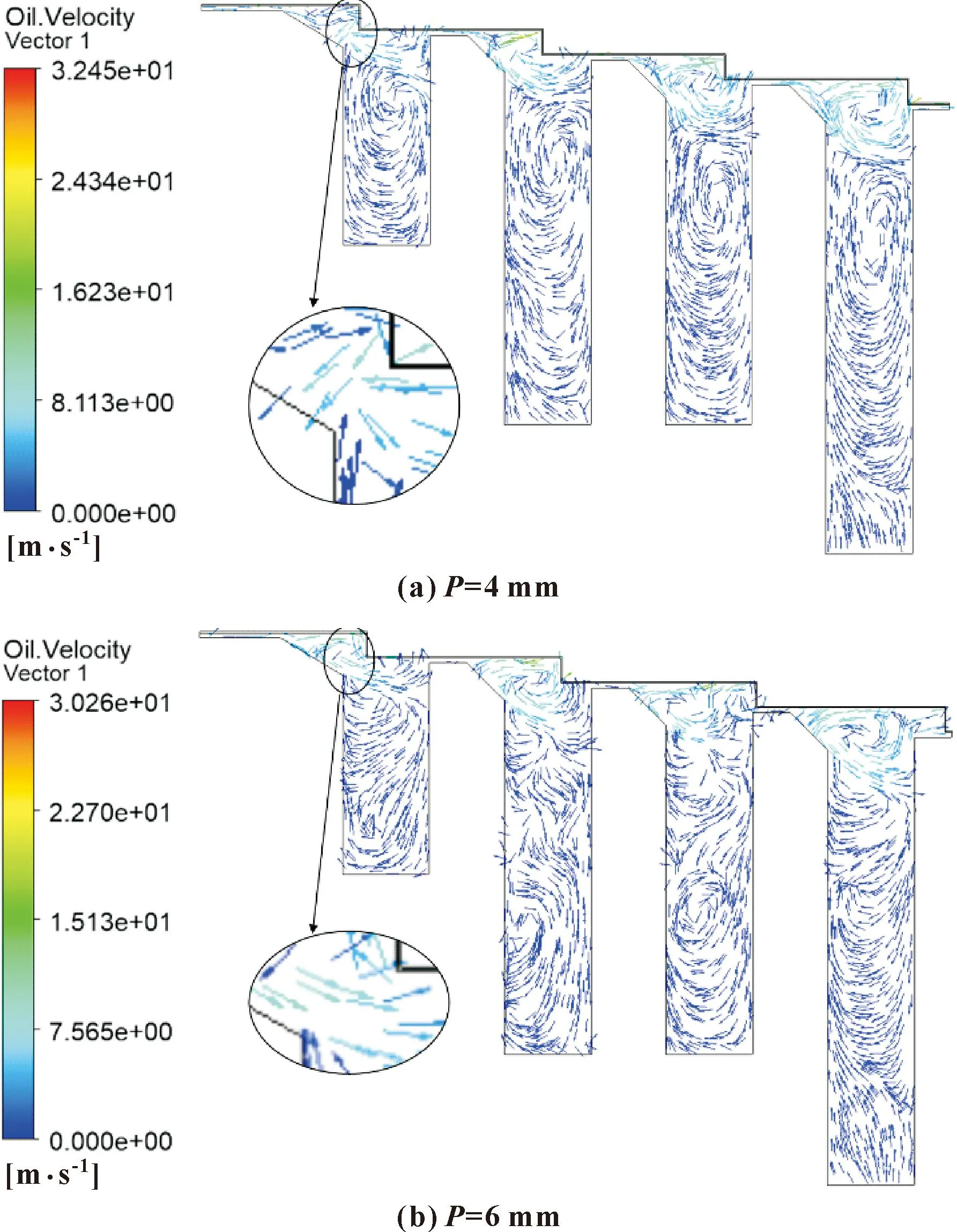
图28 不同齿与台阶距离下油液速度矢量图

图29 齿和台阶的距离与润滑油泄漏量关系

如图29所示，随着密封齿与台阶之间距离的增加，密封结构的泄漏量逐渐增大。这是因为密封齿与台阶的距离增加，使它们之间形成的间隙增大，进而使该处节流作用减弱，导致单位时间内油气混合物进入空腔的总量增多，而空腔的动能耗散作用有限，最终使润滑油泄漏量增加。综合考虑迷宫密封性能和制造装配难度，齿与台阶间的平均距离应选择4 mm。

5.4 齿宽对轴向迷宫密封性能的影响

采用3.2节的仿真条件，以原始模型齿宽5 mm为中间值，建立齿宽分别为4、4.5、5、5.5、6 mm的5组模型，并对其进行数值模拟。图30给出了齿宽分别为4和6 mm的油液速度矢量图，齿宽与润滑油泄漏量之间的关系如图31所示。

图30 不同齿宽下油液速度矢量图

图31 齿宽与润滑油泄漏量关系

如图31所示，随着齿宽的增大，润滑油泄漏量呈逐渐增加的趋势。增大齿宽尺寸会使轴向迷宫密封结构的空腔宽度减小，涡流形成的难度增加，进而使得空腔动能耗散作用减弱，导致润滑油泄漏量增加。为了最大程度提升密封性能，齿宽选取4 mm为宜，如果加工条件允许，3 mm或2 mm更佳。

5.5 密封间隙对轴向迷宫密封性能的影响

迷宫密封模型采用3.2节的仿真条件，以原始模型密封间隙0.5 mm为中间值，分别建立密封间隙C为0.2、0.3、0.5、0.7、0.9 mm的5组模型，并对其进行仿真。图32给出了密封间隙分别为0.2和0.9 mm的油液速度矢量图，密封间隙和润滑油泄漏量之间的关系如图33所示。

图32 不同密封间隙下油液速度矢量图

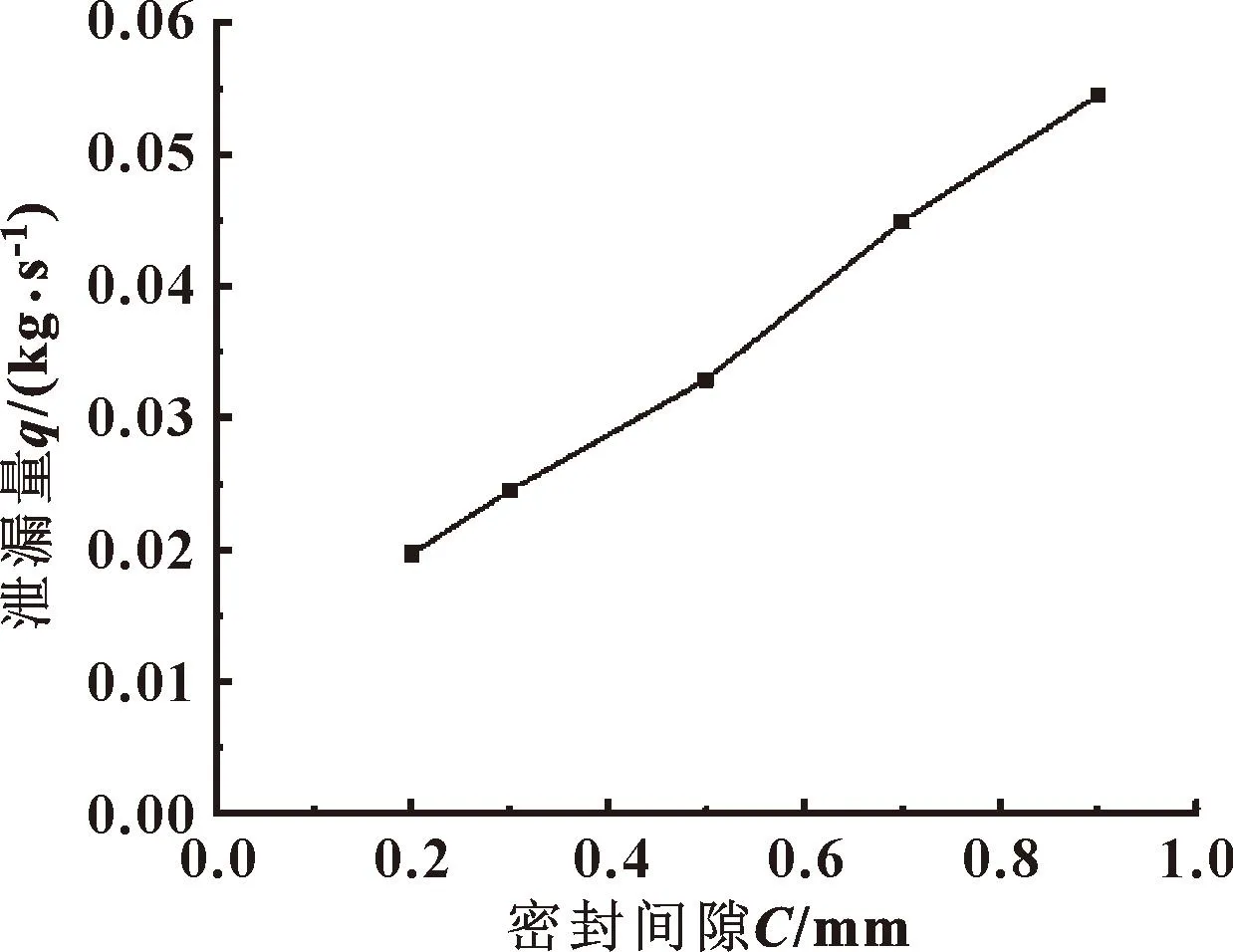
图33 密封间隙与润滑油泄漏量关系

由图33可知，轴向迷宫密封润滑油的泄漏量和密封间隙近似呈线性关系。随着密封间隙的增大，节流齿的节流作用被减弱，整个密封结构直通效应增强，最终导致润滑油泄漏量增加。综合考虑迷宫密封性能和保证转子、静子运动不干涉，密封间隙应选择0.3 mm。

综上所述，当相对啮合深度大于0.5时，润滑油泄漏量与相对啮合深度呈负相关；润滑油泄漏量与齿厚、回油孔直径、回油孔数量呈负相关；润滑油泄漏量与径向间隙、齿宽、齿与台阶距离、密封间隙呈正相关。综合考虑，相对啮合深度宜取0.7，齿厚宜取14.5 mm。回油孔直径宜取5 mm，回油孔数量宜取4个，齿与台阶平均距离宜取4 mm，齿宽宜取4 mm，密封间隙宜取0.3 mm，径向间隙宜取0.5 mm。

6 迷宫密封结构参数改进效果仿真分析

对高速列车齿轮箱迷宫密封结构参数改进情况如表3所示。由表4建立改进后的迷宫密封模型如图34所示。

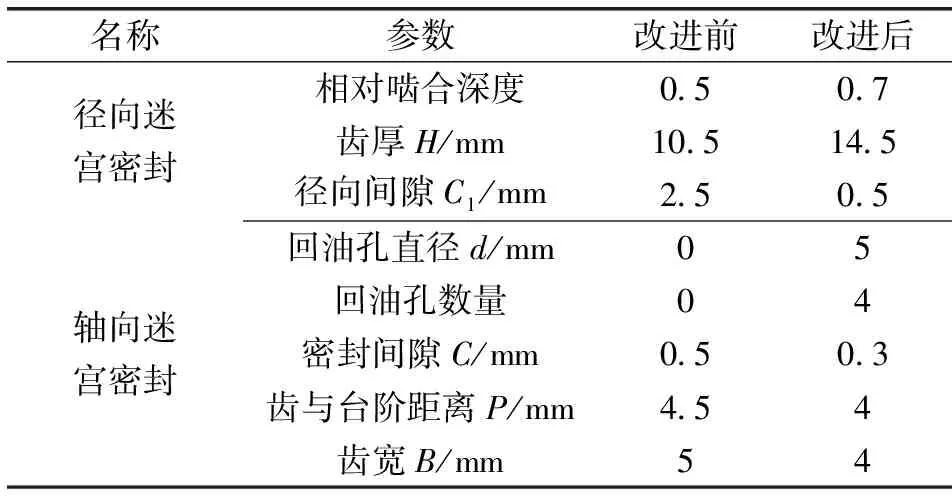
表3 改进前后迷宫密封结构参数

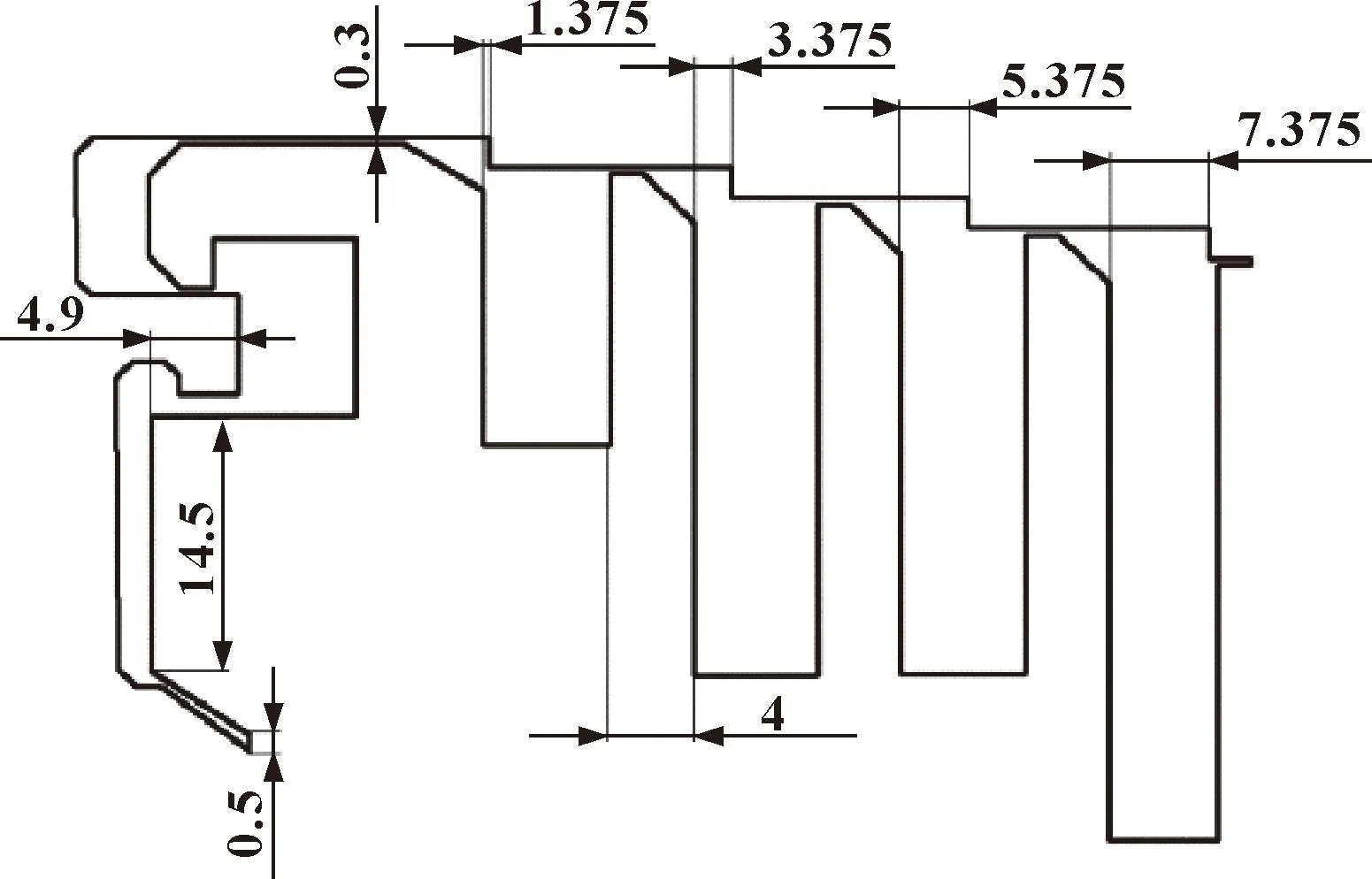
图34 改进后迷宫密封结构(mm)

采用3.2节的仿真条件，对改进后的模型进行仿真分析，其压力云图和油液速度矢量图分别如图35、图36所示，图37给出了迷宫密封结构改进后泄漏量随时间变化的曲线。

图35 改进后迷宫密封结构压力云图

图36 改进后迷宫密封结构油液速度矢量图

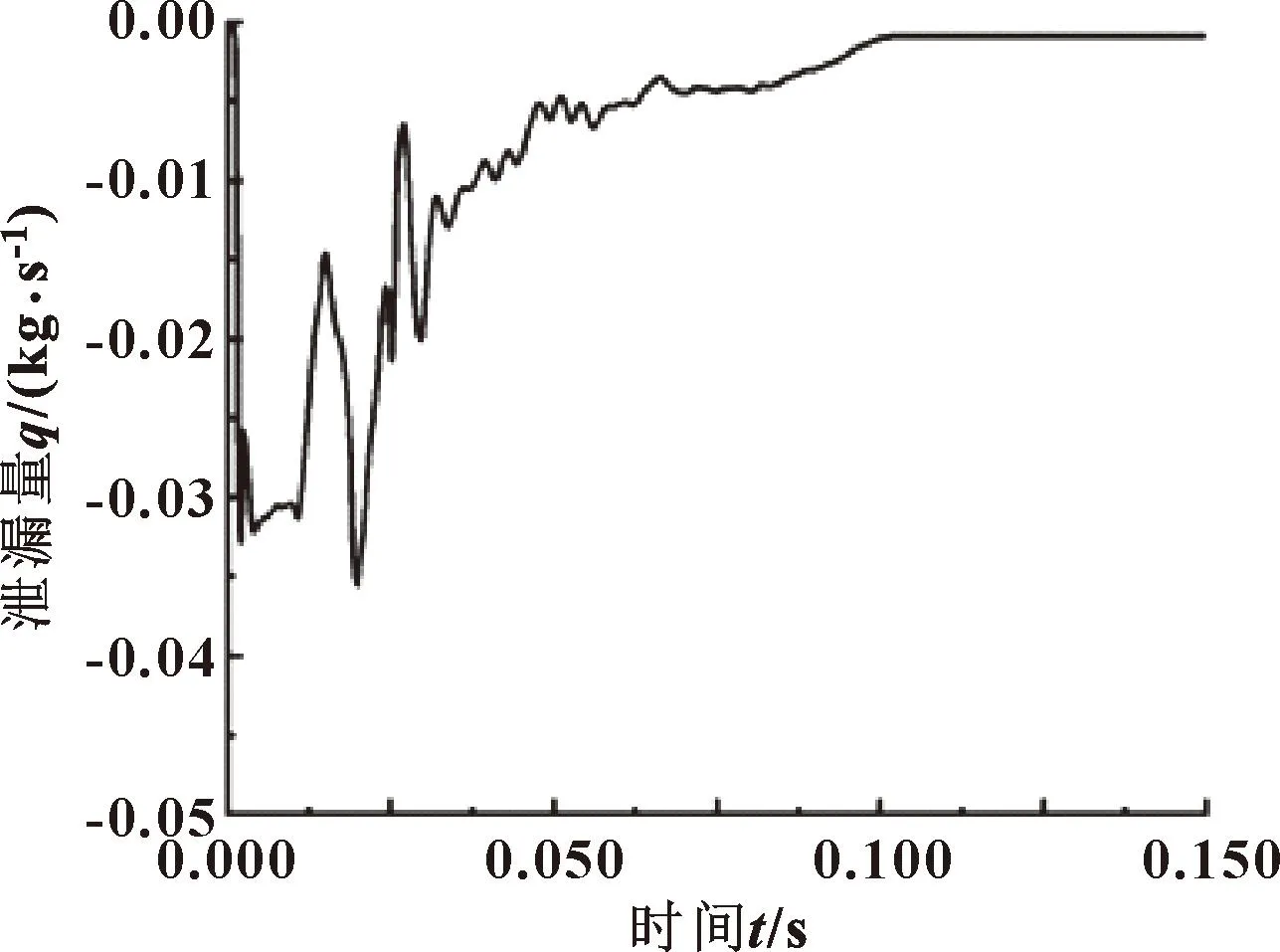
图37 迷宫密封结构改进后润滑油泄漏曲线

如图35所示，由于回油孔的存在，使得改进后轴向迷宫密封部分的空腔压力较低。

如图36所示，高流速油液主要分布在径向密封和轴向密封的第一个空腔内。这说明改进后的迷宫密封结构，径向迷宫密封部分和轴向迷宫密封的第一个空腔承担着主要的密封作用。如图37所示，迷宫密封润滑油泄漏量稳定时段的平均值为0.000 9 kg/s，降为改进前迷宫密封润滑油泄漏量的3.6%，整体迷宫密封性能得到了提升。

7 结论

(1)针对某高速列车齿轮箱的迷宫密封润滑油泄漏问题，基于ANSA软件建立了齿轮箱及迷宫密封结构的流场有限元模型。直通式迷宫密封泄漏量的仿真值与理论计算值接近，说明文中仿真方法用于模拟迷宫密封泄漏量可行。

(2)迷宫密封结构参数对泄漏量的影响存在规律性。当相对啮合深度大于0.5时，润滑油泄漏量与相对啮合深度呈负相关；润滑油泄漏量与齿厚、回油孔直径、回油孔数量呈负相关；润滑油泄漏量与径向间隙、齿宽、齿与台阶距离、密封间隙呈正相关。

(3)对迷宫密封结构进行了改进，得到的优化结构参数为相对啮合深度0.7、齿厚14.5 mm、回油孔直径5 mm、回油孔数量4个、齿离台阶距离4 mm，齿宽4 mm、密封间隙0.3 mm、径向间隙0.5 mm。优化后迷宫密封结构润滑油泄漏量稳定时段的平均值为0.000 9 kg/s，降低为原始密封结构漏油量的3.6%。