有效利用“情境串” 助力模型意识培养

王语菲 叶建云

“分一分（二）”是三年级下册第六单元“认识分数”的第二课时。与前两节课相比最大的不同就在于“整体”由之前的单个物体或图形，扩展为多个物体或图形。本节课教材共设置了三个问题，第一个问题“每种颜色占这个图形的几分之几？”主要是复习分数的面积模型。第二个问题“每种颜色的小正方形分别占9个小正方形的几分之几？”是在面积模型的基础上，引导学生认识并理解分数的集合模型。此环节重点要让学生感受到整体由一个物体或图形，变成了多个物体或图形。第三个问题“观察下图，你能得到哪些分数？”是在集合的背景下用分数表示集合中的部分事物，是巩固和应用的环节。三个问题按照“复习—拓展—应用”的逻辑顺序，层层递进，逐步加深学生的理解，丰富学生的体验。

模型思想的建立是一个循序渐进的长期过程，要让学生对模型的感悟真正发生，需要在教学中注意根据学生的年龄特点逐步渗透。本节课根据中段学生数学学习的特点，通过设计学生感兴趣的“情境串”：巧克力工厂一日游，由具体、生动、形象的事例开始，教学中借助动手操作予以模型意识内化和强化。“情境串”的设计打破了知识与生活之间的壁垒，既切合学生生活实际，又能吸引学生兴趣，帮助学生在学习中潜移默化地建立分数模型，并学会用数学语言对生活中的分数现象进行简化和描述。

一、创设生活情境，巧妙形成分数的面积模型

师：上一节课我们认识了分数。学校为庆祝儿童节，计划给同学们发放巧克力，但巧克力工厂遇到了一些问题需要我们帮助解决，让我们一起去巧克力工厂看看吧。

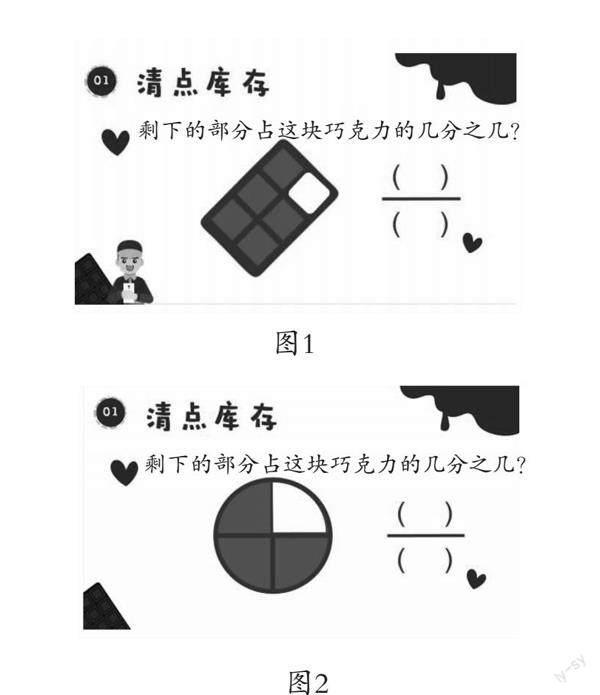
师：进入工厂我们首先遇到了仓库管理员，他想请同学们帮他清点一下库存，谁来帮帮他？（播放管理员动画）

生1：（图1）六分之五。

师追问生1：占谁的六分之五？

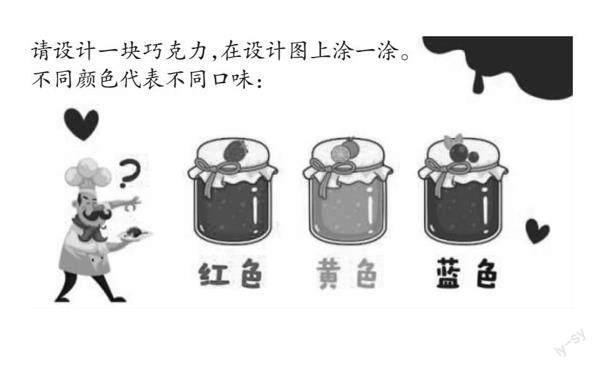
生2：（图2）这块巧克力被平均分成了4份，还剩3份，所以剩下的部分占巧克力的四分之三。

师：同学们不仅说出了对应的分数，还解释清楚了分数的意义，太棒了！告别管理员我们来到了设计室。巧克力设计师很苦恼，他正打算制作一块混合3种口味的巧克力。请你们帮他设计一块巧克力，在1号任务单上涂一涂，不同颜色代表不同口味，你想怎么涂？

【学生活动】任务单1，动手涂色找分数。

师：先请同学们在小组内交流一下自己的设计情况。（生组内交流）

师：老师请几位同学来说一说你是怎么设计的，出现了哪些分数？（选3人，注意选取两张分数一样，涂色不一样的）

生1：我是这样的，红色部分占图形的，因为把这块巧克力平均分成9份，其中红色的有4块；黄色和红色一样有4块，黄色部分占，蓝色部分占。

师：这位同学既说清楚了分数，也解释清楚了含义，真了不起。

生2：红色部分占巧克力的，因为这块巧克力被平均分成了9份，红色的有3份；蓝色和黄色也都是3块，所以都是占巧克力的。

生3：我设计的巧克力红色部分占，黄色和蓝色也是都占。

师：请同学们关注下第2和第3位同学的作品，你有什么发现？

生：他们的分数都是一样的，都是。

师追问2：分数都是一样的，但涂出来的图案怎么不一样。为什么同样的分数涂的却不一样呢？

生：每个颜色的位置不一样，但每个颜色的个数是一样的，我觉得只要将这块巧克力平均分成9份，取其中的3份，都可以用来表示，与格子的位置无关。

师小结：原来，涂色的位置对我们的分数没有影响。只要是把一个物体平均分成9份，其中的3份都可以用来表示。感谢同学们的精彩分享，看来同学们对分数有了初步的认识，在巧克力这样一个物体里找到这么多分数。

评析：此环节旨在复习表示分数的面积模型，让学生再次经历“创造分数”活动，并深度挖掘他们生成的素材，加深他们对分数的理解：表示一个整体和它的部分之间的关系。本环节设置了教师的2个追问，首先第一个追问旨在明确在面积模型中，分数的整体是整个物体或图形；第二个追问是复习分数的分母与分子的意义，深入理解分数本质，提高学生的分析、迁移能力和自主探索能力。

二、敢于动手操作，适机深化分数的集合模型

1.分一分，体验整体的变化，主动探索分数意义

师：完成设计图后，我们前往切割间。把你的设计图沿着边线剪开，剪开后看看这些小正方形巧克力，你还能找到分数吗？在這个环节，请你先剪一剪，并在桌面摆好，最后把找到的分数填在任务单2中。

【任务2：每种颜色的小正方形巧克力分别占9块巧克力的几分之几？】

【学生活动】四人小组组内合作学习。

小组汇报。

师：哪个小组来分享你们小组的学习成果呢？

生分享。

师适时追问：为什么呢？挑一个你喜欢的颜色来解释一下。

生：1个大正方形变成了9个小正方形，其中1个小正方形就是这些小正方形的，蓝色有5块小正方形，所以蓝色小方块占这些小正方形的。

2.类比、分析，加深对分数的含义的理解

师：请同学们观察对比一下自己的两张任务单上的分数，你有没有什么发现？

生：我发现两张任务单上填的分数都一样。

师：谁跟他有一样的发现呢？这么多同学都有这样的发现。老师也设计了一块，并把它剪开，我发现我的红色部分都是九分之三。为什么会这样呢？请同学们小组讨论。这两个有什么不同？

生1：原来是一个图形，现在变成了9个图形。

生2：没剪开前，红色部分占这个图形的；剪开之后，红色小方块占这些小正方形的。

师追问：在任务单1中的9在哪？剪开后9在哪？

生1：它们的整体不一样了。

生2：没剪开之前，整体是一个图形。剪开之后，整体变成了9个小方块。

生3：剪开前表示的是把一个大正方形平均分成9份，红色部分有3份，所以红色部分占大正方形的。剪开后，大正方形变成了9个小方块。红色的小方块有3个，所以红色小方块占9个小方块的。

师小结：也就是说把一个图形（板书：一个图形）看成一个整体。也可以把一些图形看成一个整体（板书：一些图形）。像这样，我把一些正方形看作一个整体。我们在这个整体中找到很多分数。（板书：整体）我们通过自己的思考和探索，能运用分数表示事物间的联系。那这样生活中很多现象都能用分数表示了。

评析：此环节中将大正方形剪成了9个小正方形，产生的变化是原来的整体变成了9个小正方形组成的一个整体。学生能够很容易地说出红色方块占全部的，但也很容易混淆面积模型与集合模型下分数的意义。所以此处设置追问，引导学生加以区分，让知识从课本延伸至生活之中，从中深化分数的集合模型。

三、放手寻找“分数”，适时强化分数的应用模型

师：我们继续前进，来参观工厂的展示柜，你还能找到分数吗？请跟同桌说一说你把什么看作一个整体？找到了哪个分数。

生1：我发现图中有5个小朋友，其中男生有2人，所以男生的人数占总人数的。

师追问：在这个小朋友的眼中，把什么看成了一个整体？那后面回答时我们先说说把什么看作一个整体，再说找到的分数，可以吗？

生2：我发现图中有5盆花，其中红花是。

师：为了让别人听得更清楚，我们可以用这样的句式：

（板：   占   的几分之几）你能再完整地说一说吗？

师：用上这样的句式，一点一点纠正，我们说得越来越标准了。

……

师小结：生活中的分数太多了。在找分数之前首先要确定把谁看作一个整体，确定整体和个体之间的关系，从中发现分数。

评析：此环节旨在让学生在发现——思考——交流的过程中，逐步认识和理解把多个物体看作一个整体，平均分成若干份，其中的一份或几份也可以用分数表示。此环节引导学生在解决实际问题中感悟数学模型思想，通过具体的“你还能找到分数吗”这个问题，让学生在图中寻找该分数的意义，一方面可以给学生做一个典型的示范，另一方面可以引导学生聚焦于图中的数学信息。引导学生通过观察和学习，抽象出更为一般的分数模式表达，经历不断对表达模型建立和修正的过程，从中适时强化分数的应用模型。

四、分层巩固练习，适度拓展分数的应用模型

练习一：巧克力工厂有新的订单了！让我们看看是第几组的同学能抢到这份订单。

【互动游戏判断练习】

判断1：在分数中，整体可以是多個物体。

判断2：一共7只蝴蝶，白蝴蝶有3只。白蝴蝶占全部蝴蝶的七分之三。

判断3：3个女生5个男生，女生占总人数的五分之三。

练习二：移一移，填一填。

师：请同学们根据客户要求将巧克力移入包装盒。

生自主完成，全班汇报。

师：我们从图中能找到分数，也能根据分数想出画面，了不起啊！

总结：同学们，今天我们学习的知识和以往有什么不同？通过今天的探索，你有什么感受？

生1：分数的整体发生了变化。

生2：我能快速地在图中找到部分和整体间的关系。

评析：通过基础练习和提升练习，检查学生对所学知识掌握情况，加深学生对分数的含义的认识和理解，引发学生的共鸣，进一步认识到学习分数的必要性，从而适度拓展分数的应用模型。