把握数量关系 发展模型意识

林清 徐慧丽

《义务教育数学课程标准（2022年版）》指出：模型意识主要是指对数学模型普适性的初步感悟。知道数学模型可以用来解决一类的问题，是数学运用的基本途径；能够认识到现实生活中大量的问题都与数学有关，有意识地用数学的概念与方法予以解释。现以“混合运算”第一课时“乘加、乘减混合运算及其运用”为例，探讨教学中如何促进学生模型意识的形成，提升思维品质，引领问题解决。“乘加、乘减混合运算及其运用”这部分内容，是在解决现实问题的过程中，经历抽象出混合算式的过程，理解混合算式的意义和运算顺序。乘加、乘减混合运算的本质就是加法模型“总量=分量+分量”，在以往的教学过程中，教师受限于传统教学方法，学生对相关科学概念的理解仅停留在表面，也很少能够通过模型意识的渗透建立新旧知识之间的联系。所以这节课尝试从沟通新旧知识之间的联系出发，保持数量关系教学的整体性和一致性，引领问题解决，从中发展学生的模型意识。

一、回归数学概念本质，渗透模型意识

模型意识是指学生对数学模型普适性的初步感悟，是形成模型观念的基础。教师在课堂教学中要注重回归概念本质，在学生积极、主动参与学习过程中渗透模型意识。例如，本课伊始，教师进行以下教学片段：

师：同学们在一年级就已经学习过了加法的意义，你能用语言和手势表示加法的意义吗？

生：加法表示將一部分数量和另一部分数量进行“合并”，数量会增加。（同时用手势表示）

师：我们可以用这样一个简单的式子“总量=分量+分量”来表示你刚才所描述的加法的意义，我们称之为加法模型。

师：我们生活中有很多情境和问题都可以通过这个加法模型来解决，你能举例吗？

以上教学过程，教师“瞻前顾后”，在引导学生进行知识回顾的过程，渗透模型意识，初步建立新旧知识之间的联系，为建构完整的“总量=分量+分量”的加法模型做铺垫。

二、经历数学建模过程，培养模型意识

教师在小学数学课堂教学过程中，要结合学生年龄特征和学习内容，让学生在数学学习中经历数学建模的过程，感受数学模型的优越性，形成初步的模型意识。

1.构建加法模型原始问题。

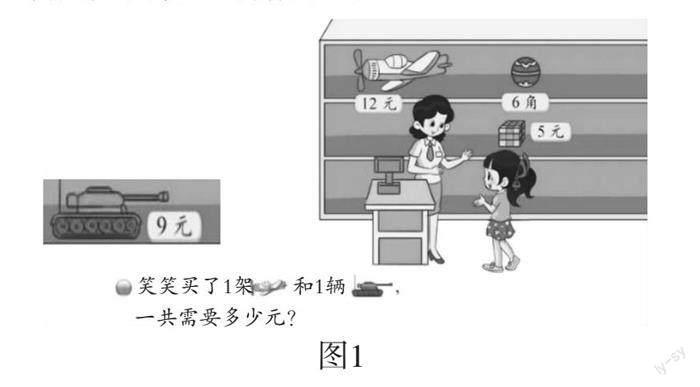
课件出示例1图片和问题。

师：这是我们二年级上册解决过的一个问题，解决“笑笑一共需要多少元”这个问题的思路是什么？

生：用1架飞机的价格加1辆坦克的价格就是总价钱。

教师板书：1架飞机的价格+1辆坦克的价格=总价钱

师：如何用算式来表示？

生：12+9=21（元）。

以上教学过程，教师再次使用二年级课本中出现的情境作为原问题，建立新旧知识的联系，旧问题、新解决。通过问题，引领学生把握数量关系，并通过板书“1架飞机的价格+1辆坦克的价格=总价钱”将数量关系从语言表征过渡到符号表征，再次渗透模型意识，将实际问题进行了结构化。

2.改变原始问题的条件。

师：如果我把问题中的1辆坦克变成2辆坦克。

课件出示例2：笑笑买了1架飞机和2辆坦克，一共需要多少元？

师：要想解决这个问题，需要什么信息？

生：需要知道一架飞机12元（飞机的价格），一辆坦克9元（坦克的价格）。

师：解决这个问题的思路是什么，你能找到信息和问题之间数量关系吗？

生：2辆坦克的价钱和1架飞机的价钱就是总价钱。

教师板书：2辆坦克的价格+1架飞机的价格=总价钱

师：如何根据上面这个数量关系列算式？

个别作品展示，组织学生交流算式的意义，探讨混合算式的运算顺序。

算式一：

9×2=18（元），12+18=30（元）。

算式二：

9×2+12=30（元）。

算式三：

12+9×2=30（元）。

师：以上这三个算式的结果都是一样的，先计算什么？再计算什么？

生：都是先算2辆坦克的价钱，然后再计算2辆坦克和1架飞机的总价钱。

师：你认为这道题符合我们的加法模型“总量=分量+分量”吗？两个分量分别是什么？

生：这两个分量分别指2辆坦克的价钱和1架飞机的价钱。

师：那如果买3辆坦克和1架飞机；

4辆坦克和1架飞机；

……

解题思路是否一致？先算什么？再算什么？

以上教学过程，通过改变原始问题的条件，让学生在变中发现实际问题的模型（数量关系）没有变，都是用若干坦克的价钱+1架飞机的价钱=总价钱，从而感受数学模型和实际问题之间的关系，拓展了学生的思维。

3.变换信息和问题。

课件出示例3：笑笑有30元，正好买了1架飞机和2辆坦克，一辆坦克9元，一架飞机多少元？

师：如果我把这道题的信息和问题进行变换，你能找到这道题的数量关系吗？

生：跟刚才那道题的数量关系是一样的，因为30元正好买了1架飞机和2辆坦克，所以1架飞机的价格+2辆坦克的价格=总价钱。

师：如何根据数量关系解决这道题？

生：加减法是互逆的，用30元减去2辆坦克的价钱，就是1架飞机的价钱。

师：列算式并计算。

学生自主完成，教师进行作品展示，全班交流乘减混合算式的意义和运算顺序。

师：仔细观察这三个例题和所对应的数量关系，有什么相同或者不同，它们的算式是否都可以用我们的加法模型“总量=分量+分量”转换而来？

生：虽然信息和问题在变化，但是它们的数量关系是一致的。

以上教学过程，通过对一个问题进行扩展、互逆等各种变换，让学生保持同类问题的解决思路，当遇到更复杂的问题时，也能从更高的层面上，运用数学模型解决问题。

三、重视数学模型运用，强化模型意识

模型意识是学生沟通数学与现实生活的重要桥梁，是实现跨学科主题学习的一大助力，同时也是初中阶段学生形成模型观念的经验基础。教师在教学过程中、特别是练习、运用环节，要注重拓展生活情境，重视数学模型运用，从中强化模型意识。

如，本课的练习，可以这样进行设计：

1.说一说，再列式算一算。

2.想一想，应找回多少元？

3.一共能坐多少人？

以上教学过程，教师先是让学生用图来直观展示情境中所蕴含混合运算中的加法模型；同时情境中隐含事物有规则地排列，从形的角度再次体会乘法的意义。此外，多样化的生活情境，让学生体会到问题背景不同，但数学结构相同时，可以采用相同的方法解决，建立起“总量=分量+分量”这个数量关系的深刻认识。

总之，培养学生的数学模型意识，既是数学教学的核心目标之一，也是发展学生数学核心素养的表现之一。