基于循环神经网络的弹药着速预测

王现磊，王义江，陈春江，吴家健

（解放军63861 部队，吉林 白城 137001）

0 引言

在武器系统试验靶场，获取高精度弹道参数是评定和分析武器打击精度的重要内容［1］。而弹药的着速是影响目标毁伤程度的重要参数之一，因此，精准获取弹药的着靶速度成了重要研究目标。目前靶场大多采用梳状靶、电探针等区截装置接触式测量法［2］，测量值与真值相差较大；高速摄影装置可以对弹药飞行过程实时记录其影像，但人工判读底片过程，不可避免引入一定程度的测量误差［3］；连续波测量雷达是获取弹药径向速度的重要途径，具有测速精度高的优点，但是立靶对雷达回波信号产生较大噪声和干扰，后续对弹药着速的提取依赖于信号的滤波、特征点的提取以及对数据处理的经验，其精度受到不同程度影响。本文通过使用雷达采集的时间速度序列数据，将循环神经网络应用于弹药着速的预测，以期提高弹药着速的精确性，具有较大的理论意义。

弹药飞行的速度数据，具有三大特性：随机性、连续性和周期性。当前时间点的速度受到温度、风速等空气动力学因素的影响，速度数据具有随机性；相邻时间速度的值是连续的，具有时间依赖性，因此，具有连续性；周期性是指时间速度数据呈某种趋势的现象，因此，将速度数据作为时间序列进行分析与预测具有可行性，利用RNN 对弹药着速进行预测，并与RFR 算法和基于BP 的MLP 模型预测结果进行对比，取得了满意的拟合效果，对弹药后续指标的评估具有实用价值。

1 时间序列预测

时间序列预测的方法主要包括基于数学理论模型的预测方法和基于大数据驱动预测方法［4］。数学理论模型预测方法主要基于数学和统计学等知识，仅从时间的维度对被预测对象建模，对复杂时间序列数据难以建立精确的数理统计模型，适用性受到极大限制且预测精度大大降低。基于大数据驱动预测的方法主要有传统机器学习方法、前馈神经网络方法和循环神经网络等［5］。传统的机器学习方法，如线性回归、支持向量机、随机森林等算法［6-8］，对于时间序列的处理，是利用数据中的维度特征，进而构建起从因变量到目标预测值的函数方程，通过不断优化构建的损失函数，来构造回归模型。但是该类模型在建模时仅考虑时间序列当前时间点的特性，忽略了数据彼此间具有时间依赖性，因此，预测精度不高。

神经网络是一种由大量运算节点之间互相连接构成的运算模型。每个节点代表一种特定的输出函数，即激励函数。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆。网络的输出则以网络的连接方式、权重值和激励函数的不同而不同。而网络自身通常都是自然界某种算法或者函数的逼近，也可能是一种逻辑策略的表达［9］。神经网络模型的神奇点就在于它是一个“黑盒”模型，输入大量历史数据，模型就可以自动学习到序列之间的规则以及依赖关系。神经网络方法弥补了传统统计模型固有的劣势，可以处理具有非线性模式数据。根据需要，仅对前馈神经网络做简单介绍。

2 前馈神经网络

2.1 多层感知机

人工神经网络（artificial neural network，ANN）由神经生理学家Warren McCulloch 和数学家Walter Pitts 于1943 年首次提出，通过对生物神经元进行建模，首次提出了一种形式神经元模型；1957 年Frank Rosenblatt 提出了感知机，感知机是最简单的ANN架构，能够确定神经元的连接权重，但无法解决线性不可分问题，基于此人们提出了MLP 模型，也称为前馈网络模型。MLP 通常采用3 层结构，由输入层、隐藏层及输出层组成。如图1 所示。

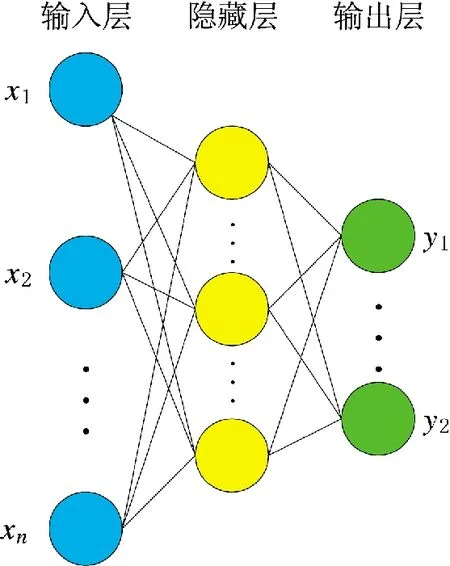
图1 多层感知机模型Fig.1 Multi-layer perceptron model

输入层表示神经元接受x1，x2，…，xn作为输入，隐藏层通过权重与输入层的各单元相连接，通过激励函数计算隐藏层各单元的输出值，同样通过权重与输出层相连接。由于模型的输出与模型自身之间不存在反馈过程，因此，被称为前馈神经网络。

2.2 误差反向传播算法

1986 年 David Rumelhart、Geoffrey Hinton 和Ronald Williams 发表的开创性文献［10］介绍了误差反向传播训练算法，该算法能够针对每个模型参数计算网络误差的梯度，并通过比较实际输出和期望输出得到误差信号E，把误差信号从输出层逐层向前传播得到各层的误差信号，再通过调整各层的连接权重以减小误差。其权重的调整主要结合梯度下降法，过程如图2 所示。

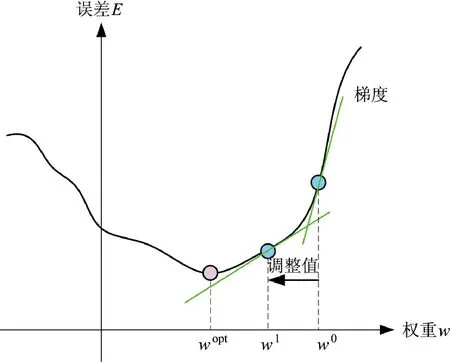
图2 梯度下降法Fig.2 Gradient descent method

通过实际输出和期望输出之间的误差E 和梯度，确定连接权重w0调整值，得到新的连接权重w1，然后反复不断地调整权重以使误差E 达到最小，并从中学习得到最优的权重连接wopt，即网络收敛到最优解。

3 着速预测网络模型

3.1 模型介绍

着速预测网络模型是一个从序列到向量的网络，由连续波雷达采集的时间速度数据作为输入序列，并忽略弹药着速外的所有输出，即忽略飞行过程的速度值，输出着靶速度。其模型按时间展开的网络如图3 所示。

图3 时间展开的网络模型Fig.3 Network model of time expansion

图3 为含有一层循环神经网络、若干隐藏节点的着速预测模型。其中，损失衡量序列结束时的输出与相应的训练目标的距离；U 表示RNN输入层到隐藏层的连接权重矩阵，W 表示隐藏到隐藏的循环连接权重矩阵；V 表示隐藏到输出的连接权重矩阵；f 为激活函数；为记忆单元且满足式（1），即在时间步长t 时刻递归神经元的输出是先前时间步长中的所有输入函数

式中，b 为偏置向量。

3.2 评价指标

为量化实验结果便于比较，本文选取了预测问题的典型性能指标均方根误差（RMSE），其公式如下：

4 实验及结果分析

4.1 数据集说明

实验选用某型穿甲弹连续波雷达采集并处理后的速度数据共计60 发，作为实验数据集，每发弹的数据格式为等间隔的、连续的81 个时间速度点，其中，最后一点为弹药着靶速度。随机选取42 发（占70%）作为训练集，6 发作为验证集，剩余12 发（占20%）作为测试集。样本输入特征（x_train，x_valid，x_test）为［42，80，1］，即总共42 发数据，每发前80 个点作为输入样本，维度为1；输出特征（y_train，y_valid，y_test）为［42，1，1］，即每发弹药的着靶速度，共计42 发。

4.2 模型超参数设置及训练

激活函数选择不同会导致梯度不稳定问题，通过控制变量方法，为着速预测网络模型选取ReLU 激活函数，并使用其初始化策略即He 初始化；对比常规梯度下降优化器，选取Adam 优化器加快训练速度，由于Adam 是一种自适应学习率算法，因此，不对学习率超参数η 进行调整，使用其默认值η=0.001。

本实验中多层感知机模型和预测网络模型的隐藏层数（n_hidden）与每层包含的神经元数（n_neurons），采取RandomizedSearchCV 探索超参数空间，如表1 所示。

表1 超参数空间Table 1 Hyperparametric space

设置n_hidden：［0，1，2，3］，n_neurons 为［0，100］，设置最大迭代次数为200，当损失值连续10 次未发生改变或至最大迭代次数时，尝试其他超参数组合，结束并输出最佳超参数组合。

经过RandomizedSearchCV 探索超参数空间，多层感知机模型和着速预测网络模型返回最佳超参数组合及超参数设置如表2 所示，根据训练过程，两个模型epoch 在90 左右RMSE 值收敛于稳定状态，因此，设置epoch=110。

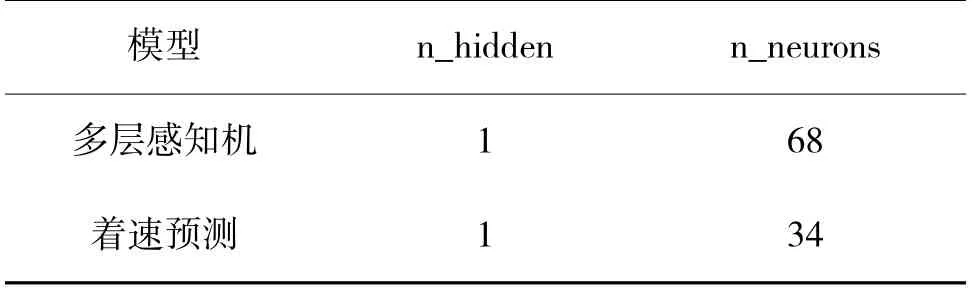
表2 最佳超参数组合Table 2 Best combination of hyperparametric

多层感知机模型和着速预测网络模型训练过程中其训练样本RMSE 曲线分别如图4、图5 所示；随机森林回归算法，通过调整参数训练样本并对测试集进行预测，其RMSE 值如表3 所示。从图中可以看出，训练样本在两种模型中RMSE 最终均趋于稳定的收敛状态，其网络学习过程较为类似，相较而言着速预测网络模型收敛速度更快；由表3 可直观的看出着速预测网络模型在测试集上的RMSE值相比其他两种更小，即拟合效果更佳。

表3 测试集RMSE 值Table 3 RMSE values of test set

图4 多层感知机训练过程Fig.4 Training process of multi-layer perceptron

图5 着速预测模型训练过程Fig.5 Training process of target velocity prediction model

着速预测模型真值与预测结果如图6 所示，实验结果表明该模型的适用性较强，可通过网络模型的不断训练较准确的学习出不同弹速的飞行规律，并给出精准的预测，由后续的测试误差图可知，该模型具有很好的稳定性。

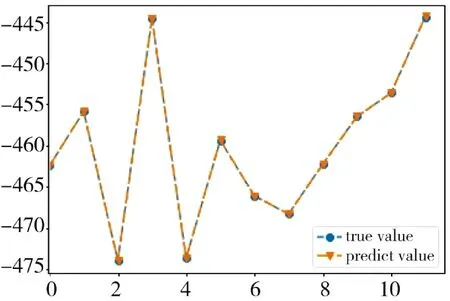
图6 着速预测模型测试结果Fig.6 Test results of target velocity prediction model

为了直观地对比3 种模型对弹药着速的预测，实验测试集误差结果如图7～图9 所示。

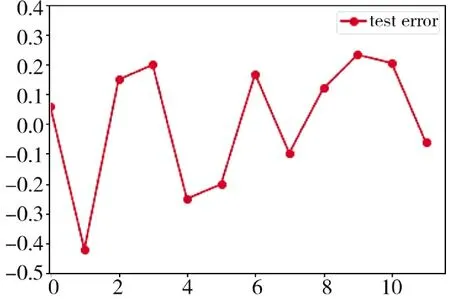
图7 随机森林测试误差Fig.7 Random forest test errors

随机森林回归算法是一种基于集成学习的监督式机器学习算法，通过加入不同或相同类型算法获取强大且稳健的预测模型，且不易陷入过拟合；但因其随机性，由图7 可知预测结果不是很稳定，有较大的波动性，该算法对测试集着速预测误差在0.2 左右。多层感知机模型，超参数空间较大且复杂，其隐藏层包含的神经元数更多，通过选择适宜的激活函数和超参数，基于BP 算法训练其模型用于着速预测，由图8 可知，测试集着速预测误差在0.15 左右，相比于随机森林回归算法预测精度和稳定性得到改善，但预测结果稳定性仍有起伏。而着速预测网络模型受益于隐藏层之间有循环连接，考虑了速度数据之间存在时序上的依赖关系，极大地提高了网络模型对速度数据的分析、学习能力和预测精度，且加快了网络模型的训练速度，从而使网络学习效果得到提高，由图9 可知，其预测误差绝对值在0.02 左右，且稳定性更好；相比于前两个算法模型，其预测精度有数量级的提升，取得了较好的实验效果，得到了更精确的预测结果。

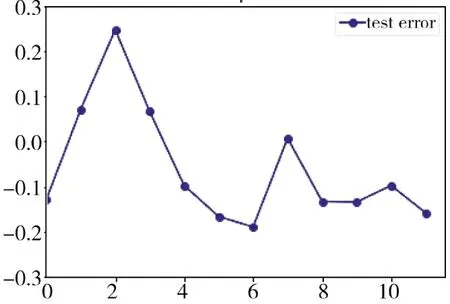
图8 多层感知机测试误差Fig.8 Multi-layer perceptron test errors

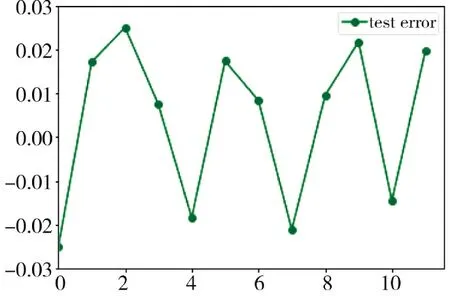
图9 着速预测模型测试误差Fig.9 Test errors of target velocity prediction model

5 结论

本文分别使用随机森林回归算法、基于BP 的多层感知机模型和基于RNN 的着速预测模型，对某型穿甲弹的着速进行预测，从预测结果分析得出基于RNN 的预测模型，可更好地从速度数据中挖掘序列之间的内部关联且模型的适应性较强，预测精度优于传统方法。实验结果表明，基于RNN 的着速预测模型，切实提高了分析预测效果，其预测结果可作为弹药着靶速度。本文构建的模型具有一定的应用推广价值，可推广应用于雷达测速数据跳点、丢失点的填补。