基于BO-LSTM 神经网络的地面无人系统网络时延分析

王鑫鑫，田卫萍，田 野，刘 超，党国龙

（北方自动控制技术研究所，太原 030006）

0 引言

近年来，随着机器学习、人工智能、远程控制、云计算、自主协同等前沿科学技术在无人系统领域的发展，催生了地面无人系统的跨越式变革［1］，地面无人系统由系统架构、运动规划、环境感知、自主控制、安全防护等多种关键技术融合而成［2］。某地面反无人机系统主要包括操控终端和地面反无人机作业车，具体组成如图1 所示。

图1 某地面反无人机系统组成图Fig.1 Composition diagram of a ground anti drone system

目前常见的地面无人系统的通信方式主要是遥控数据链［3］，为实现操作人员对多个地面无人车辆的集群控制，无线通信网络的引入是必然的发展趋势。但由于网络中各节点共享通信带宽，随着节点数量以及不同任务的差异，网络时延也会发生变化，从而影响操控系统的实时性和精度。

本文对某地面反无人机系统的传输时延进行分析，针对网络时延的随机分布特性，建立贝叶斯算法（BO）优化的长短期记忆（LSTM）神经网络时延预测模型，并在实验测试获得的网络时延样本数据集上对预测的效果进行验证。

1 网络控制地面反无人机系统

地面反无人机系统通信网络结构图如图2 所示。操控终端和地面反无人作业车之间通过基站实现无线通信。地面反无人作业车电视摄像机和红外热像仪对无人机目标进行探测和跟踪，采集并生成无人机目标视频图像信息，通过基站分配的无线信道回传给操控终端，同时，多线激光雷达等传感器采集的地面反无人作业车位置信息，网络摄像头采集的周边环境信息也通过基站分配的无线信道回传给操控终端。操控终端通过基站分配的无线信道发送操控指令，控制地面反无人作业车的行进，以及伺服转台的转动，实现对无人机目标的探测、跟踪和干扰。

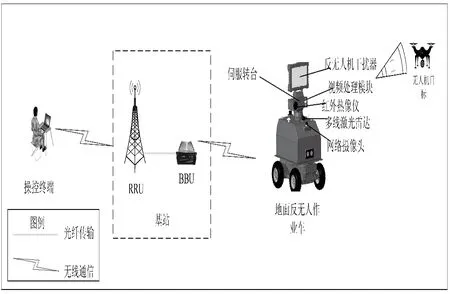
图2 地面反无人机系统通信网络结构图Fig.2 Communication network structure diagram of ground anti-UAV system

地面反无人机系统网络控制流程图如图3 所示。

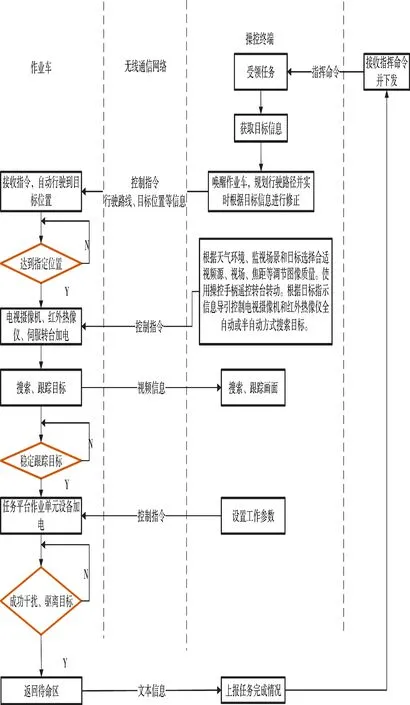
图3 系统工作流程图Fig.3 Flow chart of system operation

系统工作流程如下：

1）班组操作人员通过操控终端接收上级指挥中心下发的作业命令、目标位置信息，在对作业车上电后，根据作业车上传的车体位置信息，规划并实时修正行进路线，通过无线通信网络发送给作业车，驱动作业车行驶至指定位置，同时，操控终端接收作业车上传的视频信息。

2）作业车到达指定位置后，根据目标位置信息、周边环境信息，选择合适的视频源、视场、焦距等参数调节视频图像质量，通过操控手柄控制转台转动，使目标在光电跟踪设备视场内成像，计算目标在视场内的位置与视轴中心的偏移量，输出脱靶量信息，设置转台方位轴和俯仰轴的转动速度，通过无线通信网络发送给伺服控制系统进行补偿，将目标导引到视场视轴中心，完成对目标的探测和识别。

3）在探测和识别到目标后，由伺服控制系统控制光电跟踪设备对目标进行自动跟踪，在能够稳定跟踪后，设置作业单元的工作参数，完成对目标的干扰、迫降或驱离，然后，由操控终端向上级指挥中心上报任务完成情况。

2 地面反无人机系统时延分析

无线通信网络以基站为接入节点，在操控终端和地面反无人作业车上集成宽带通信模块，操控终端和地面反无人作业车之间通过基站实现通信。

无线通信网络工作带宽最大为20 MHz，可以接入至少64 个终端设备，支持语音调度、视频调度、视频监控、文件传输等功能。

无线通信网络具有以下几个方面的特点：1）区域宽带无线通信网络通信覆盖范围广，跨空间性高，能够克服空间和地域的限制，只要有网络的接入点，相应的软硬件，就可以构成可靠的控制系统；2）在无线通信网络中可以接入其他终端，扩展更多不同类型的业务。

相对地，由于无线通信网络本身带宽和上下行时隙配比，以及在各时隙上传输业务划分的原因，数据（尤其是数据量大的视频数据）在操控终端和作业车之间发送和接收需要花费较多的时间，此外，在数据传输的过程中，不可避免地会有数据碰撞和数据重传等问题的产生，也会增加传输的时延。由数据传输所造成的时延，主要包括数据信号的采集、量化、编码、压缩、解码以及显示的过程。

传输时延的存在会影响数据传输的实时性，使得整个地面反无人机系统存在滞后性，不能及时对任务目标情况作出决策和响应，从而会降低系统的控制性能质量，影响系统的稳定性，此外，传输时延的存在还会使系统发生空采样和多采样等问题。

在实际执行任务时，地面反无人作业车回传目标视频图像至操控终端，操作人员根据目标视频图像向地面反无人作业车发送操控指令，而视频图像信息回传和操作控制指令的传输过程，各个环节都会产生时延，具体时延组成如图4 所示。

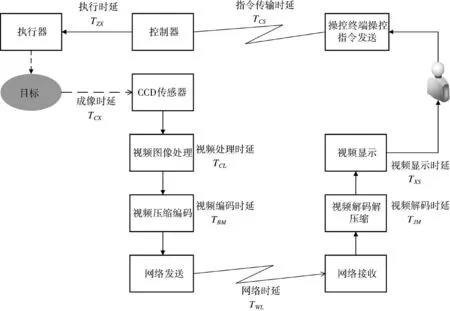
图4 地面反无人机系统时延组成图Fig.4 Time delay composition diagram of ground anti-UAV system

由图4 可知，地面反无人机系统网络控制的时延主要由两部分组成，第一部分是视频图像信息回传过程的时延，设为TH，另一部分是操控终端操作控制指令的传输时延，设为TK，则TH和TK可以由式（1）和式（2）表示，系统总时延T 可以由式（3）表示。

如图5 所示，以无人机目标在CCD 传感器上开始成像为起点，经过TH时间，无人机目标在操控终端上成像，操作人员通过操控终端向作业车发送控制指令，经过TK时间，作业车根据控制指令，开始对无人机目标进行跟踪和干扰。从无人机目标在作业车CCD 传感器上成像到作业车开始跟踪和干扰，总时延如式（3）所示，TH和TK在时间上具有连续性，TK的产生在TH时刻之后。

图5 地面反无人机系统时延关系图Fig.5 Time delay relationship diagram of ground anti-UAV system

式（1）中，TCX是地面反无人作业车上，反无人机作业单元电视摄像机和红外热像仪中CCD 传感器采集目标视频图像帧的时间，TCL是视频图像帧信号经过视频图像处理板处理的时间，TBM是视频编码器对视频图像进行压缩、量化和编码的时间，TWL是视频图像通过无线通信网络，从地面反无人作业车发送到操控终端接收的时间，TJM是操控终端在接收到视频图像后经过解码、反量化和解压的时间，TXS是视频图像在解码为视频帧信号后在显示器上输出显示的时间。

式（2）中，TCS是在看到视频画面后，操作人员通过操控终端发送操作控制指令到作业车控制模块接收的时间，TZX是地面反无人作业车在接收到操作控制指令后，发送控制指令控制伺服电机驱动转台转动的时间。

在上述时延中，伺服电机的执行时延TZX相对较小，在进行系统时延分析时，一般不考虑TZX的影响，可以忽略不计；操作人员在看到视频图像后，通过操控终端采集操控手柄转动信号，编码然后通过无线通信网络发送，操控手柄转动信号数据量相对很小，指令传输时延TCS可以忽略不计；由于视频图像数据量很大，视频压缩编码和解码的时间会相对较长，同时，无线通信网络带宽较窄，因为其他业务节点的存在，分配给视频信号传输的时隙较小，视频回传时延TH较大，因此，本文对系统时延的分析主要是围绕视频回传的时延TH展开。

在视频回传的时延TH中，成像时延TCX、视频处理时延TCL、视频编码时延TBM、视频解码时延TJM、视频显示时延TXS都以帧为单位进行采集和处理，成像时延、视频处理时延和视频显示时延取决于CCD传感器、视频处理板和显示器的硬件结构和性能，当硬件结构和性能不发生变化时，每一帧图像经过采集、处理和显示的时间是固定的；视频编解码是对视频图像帧进行压缩和重建的过程，以一部分完整帧图像为基准，对每一帧中的运动目标的位置变化作残差运算，最后获得的是一部分完整帧图像以及若干残差帧，当采用的视频编解码器和编解码标准不变时，对每一帧的压缩比例是一样的，最后获得的帧数据量基本相同，因此，视频编解码时延是基本固定的；网络时延TWL与无线通信网络的结构、当前网络中接入的业务节点的数量、当前业务信道资源的占用情况等有关，当网络的结构不发生变化时，随着业务数据量变化和信道时隙的分配，网络时延会在一定范围内随机变化。

3 地面反无人机系统网络时延预测

网络时延TWL是在一段时间内维持在一个区间内波动的随机时延，而且，在这一区间段内，网络时延具有很强的自相关性，下一时刻的时延与前一段时间的时延存在一定的非线性关系［4］，正因为这种非线性和相关性，网络时延在局部范围内是可预测的。

目前，对于网络时延数据的预测方法主要包括传统的概率统计模型、人工智能模型以及混合模型等。传统的概率统计模型包括自回归模型、滑动平均模型、自回归滑动平均模型等［5-6］，具有结构简单、计算量小、计算时间短的特点，但对于复杂度较高的时间序列数据，该模型预测精度较难保证。人工智能模型主要有决策树、支持向量机以及神经网络等［7-8］，神经网络又包括BP 神经网络、RBF 神经网络、RNN 神经网络等，神经网络是在数据预测领域的最新方法，且预测精度很高。混合模型是将各个预测算法和模型组合起来，共同对数据进行预测，可以补充单一预测模型的不足之处。

本文采用贝叶斯算法（BO）优化的长短期记忆（LSTM）神经网络对处理后的网络时延数据进行预测，LSTM 神经网络相较于BP 神经网络、RBF 神经网络、RNN 神经网络等，改善了对数据序列的长期依赖问题，缓解了在训练时反向传播带来的“梯度消失”问题，同时，其内部网络中“门”结构的设置，可以将数据的重要特征保存下来，可以实现对数据序列中数据趋势和前后相关性的挖掘，在对时间序列数据的处理和分析上具有很大优势。

3.1 自相关性检验

时延预估的前提是时延数据序列具有随机性，而且当前时刻的数据与历史数据相关，即时延数据序列具有自相关性，因此，在对时延数据进行分析和预测时，首先要对时延数据序列的自相关性进行检验。

对于一组时间序列是否具备自相关性，是通过自相关系数进行判断的，而自相关系数是通过自相关函数（ACF）获取的。时间序列的样本自相关函数的计算公式为

式中，rk是自相关系数，t 为时间序列数据的时序，k为时间滞后步长，n 表示时间序列样本数据长度，xt为时间序列在t 时刻的数值，xt+k为时间序列t 时刻滞后k 个步长时（t+k）时刻的数值，时间序列变量的均值可由式（5）进行计算。

利用式（4）和式（5），可以对时间序列数据逐个计算出自相关系数，再由这些自相关系数组成自相关系数变化图，由自相关函数变化图可以看出时间序列数据是否具备自相关性。

3.2 LSTM 神经网络

LSTM 神经网络［9］，是一种特殊的RNN 循环神经网络，关键在于“记忆细胞”的状态，通过设计“门”结构可以去除或者增加信息到“记忆细胞”状态，“门”是一种让信息选择式通过的方法，主要包括输入门、输出门和遗忘门，后续的几乎所有LSTM神经网络的设计和应用都是以这三种“门”结构为基础的。LSTM 神经网络结构如下页图6 所示。

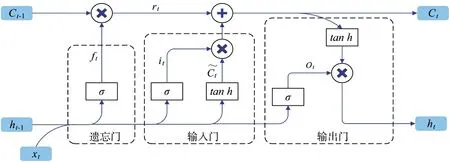
图6 LSTM 神经网络结构图Fig.6 LSTM neural network structure diagram

1）遗忘门。遗忘门决定了将要从“细胞”状态中丢弃哪些信息，计算公式为：

式中，Wfh、Wfx、bf是遗忘门的权重，ht-1为上一时刻的输出，xt为当前时刻的输入，σ 为激活函数。

2）输入门。输入门是确定需要将怎么样的新的信息保存到“细胞”状态中，计算公式为：

式中，WCh、WCx、bC是待加入“细胞”状态的信息的权重。

3）输出门。输出门是确定当前时刻隐藏层的输出ht，该输出是基于当前时刻的“细胞”状态过滤后的数值，计算公式为：

式中，Woh、Wox、bo是输出门的权重。

3.3 贝叶斯算法（BO）优化LSTM 神经网络

LSTM 神经网络的构建需要确定的超参数众多，超参数的选取对LSTM 神经网络模型的训练过程有很大的影响。在LSTM 神经网络模型的训练过程中，超参数通常由人为进行选取和调整，缺乏规律性，偶然性的成分居多，需要人为地对参数进行大量的调整和实验，且不易获得最优的超参数和训练结果，因此，采用贝叶斯算法对训练LSTM 神经网络过程中的超参数进行优化。

贝叶斯算法是对待优化函数进行近似的一种模型，是一种非常有效的全局优化方法，目标是寻找到全局最优解，主要思想是给定一个待优化的目标函数，该函数是广义的函数，只需给定输入和输出即可，无需知道函数的内部结构和数学性质，然后根据贝叶斯定理估计待优化目标函数的后验概率分布，同时，通过不断地添加样本数据对待优化目标函数的后验概率分布进行更新，即根据对目标函数过去参数信息的评估，更好地调整当前的参数信息。

核心过程主要包括概率代理模型（先验函数）和采集函数。

用贝叶斯算法优化LSTM 神经网络时延预测模型的流程如图7 所示。

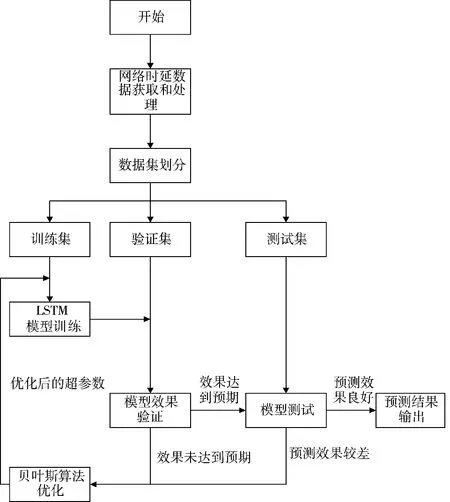
图7 贝叶斯算法优化的LSTM 预测模型构建图Fig.7 Construction diagram of LSTM prediction model optimized by Bayesian algorithm

LSTM 神经网络模型训练的过程相当于优化损失函数的过程，在设定超参数后，通过带入训练集数据，对LSTM 神经网络的权重进行更新，使得LSTM 神经网络的输出，损失函数达到最小值，贝叶斯算法的优化是为了选取最优的超参数，以提高LSTM 神经网络的训练效果。

贝叶斯算法优化LSTM 神经网络超参数的过程，首先，根据超参数的取值范围，随机产生初始的参数样本数据，代入到高斯过程中，对LSTM 模型进行训练，利用损失函数的值对高斯模型进行修正，使其更能拟合实际的数据分布；然后，选取新的一组超参数样本数据代入高斯模型，对LSTM 神经网络进行训练，输出对应的损失函数值，若符合要求，则该组超参数样本值即为最优的超参数，若不符合要求，则重新选取超参数样本数据代入高斯模型，对LSTM 神经网络进行训练，直到输出的损失函数值符合要求。

3.4 模型评价标准

为了验证贝叶斯算法优化LSTM 神经网络时延预测模型对网络时延数据预测的精确性，采用决定系数（R2）、均方根误差（RMSE）和平均绝对误差（MAE）来衡量，计算公式如式（12）～式（14）所示。

4 网络时延预测模型验证

4.1 网络时延数据样本

利用地面反无人作业车、操控终端和基站设备构建地面反无人机系统，在调整地面反无人作业车和操控终端时钟同步的情况下，地面反无人作业车发送带有时间戳的视频帧图像，发送时刻记为T1，操控终端接收时刻记为T2，则网络时延为TWL=T2-T1。

通过上述测量方法进行测试，共获得1 000 组网络时延数据，如图8 所示。

图8 网络时延测试样本序列图Fig.8 Sample sequence diagram for network time delay test

4.2 自相关性检验

基于4.1 节测量得到的网络时延数据，由式（4）和式（5）计算自相关系数，画出自相关系数变化图，如图9 所示。

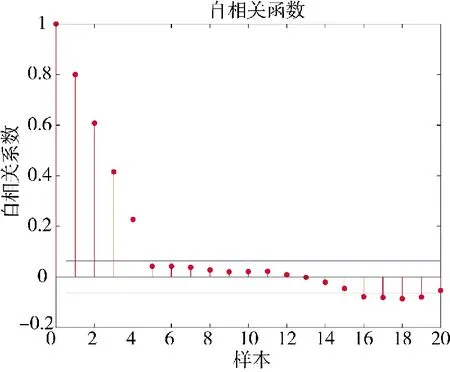
图9 网络时延自相关系数变化图Fig.9 Graph of changes in network time delay autocorrelation coefficients

当计算得到的自相关系数取值为1 时，时间序列数据为完全正相关；取值为-1 时，时间序列数据为完全负相关；取值为0 时，时间序列数据不具备相关性。由图8 可知，实验测试采集到的1 000 组网络时延数据序列自相关系数显著不为0，表明该组数据具备自相关性，每组时延数据之间存在关联。因此，可以利用实验测得的网络时延数据进行后续时延预测。

4.3 数据预处理

为提高模型的预测精度，采用平滑估计［10］的方法对上述数据进行处理，在处理过程中利用了“中位数”是均值的鲁棒思想，起到对数据类似于过滤的效果，具体步骤如下：

处理后的时延样本序列如下页图10 所示。

图10 处理后的网络时延样本数据序列Fig.10 Processed network time delay sample data sequences

采用方差（δ2）来衡量图8 中网络时延数据序列和图10 中经过平滑估计处理后的网络时延数据序列的整体波动情况，方差计算公式如式（16）所示。

式中，μ 为样本数据的平均值，N 为样本数据个数。

方差值越小，样本数据的整体波动越小，表明数据变化趋势更加平滑和稳定，能够更好地分析出数据的变化规律，能够更好地进行预测。

上述图8 和图10 两组数据的方差计算情况如表1 所示。

表1 图8 和图10 两组数据方差计算情况Table 1 Calculation of variance for two sets of data in Fig.8 and 10

由表1 可知，经过平滑估计处理的网络时延数据序列方差值小于原始网络时延数据序列方差值，表明平滑估计的数据处理方法能够过滤数据，降低样本数据的整体波动，从而提升对数据的分析和预测效果。

设定模型的输入维度为15，预测步长为1，即以连续的15 组网络时延数据作为历史数据，预测下一时刻的时延数据，与数据集中的第16 组数据进行对比。因此，划分后新的网络时延数据集共有985 组数据，每一组数据都由16 列数据组成，前15列为模型的输入，最后一列数据与模型的输出数据进行对比。

将新的985 组网络时延数据集按照7∶3 的比例划分为训练集和测试集，其中，训练集又以8∶2的比例划分出验证集数据。将训练集、验证集和测试集数据进行归一化处理。

4.4 LSTM 神经网络搭建

在基于网络时延数据样本搭建LSTM 预测模型时，需要对模型的输入层、隐含层和输出层的结构进行设计，同时，还要考虑模型在进行训练和预测时超参数的设置，训练时超参数的选取和设置如表2 所示。

表2 LSTM 模型训练超参数选取和设置表Table 2 LSTM model training hyperparameter selection and setting table

贝叶斯算法优化超参数的重点为隐含层层数、初始学习速率和正则化参数，激活函数选用tanh 函数，全连接层和回归层层数还是设置为一层，优化器选用adam 优化器，批处理大小和迭代次数根据经验公式进行设置。

4.5 贝叶斯算法优化LSTM 神经网络超参数

以交叉验证过程中用于评估训练的模型对验证集数据符合程度的均方差（MSE）指标作为贝叶斯算法优化的目标函数。

待优化的超参数约束范围如表3 所示。

表3 超参数约束范围表Table 3 Hyperparameter constraint range table

设定贝叶斯优化算法的迭代更新次数为30次，优化过程如下页表4 所示。

表4 超参数优化过程表Table 4 Hyperparameter optimization process table

在第27 次迭代时，目标函数值最小，此时，对应的超参数即为最优值，将其代入LSTM 神经网络进行训练和测试。

4.6 实验结果分析

在测试集上对训练好的模型的预测效果进行测试，预测和评估结果如图11 和表5 所示。

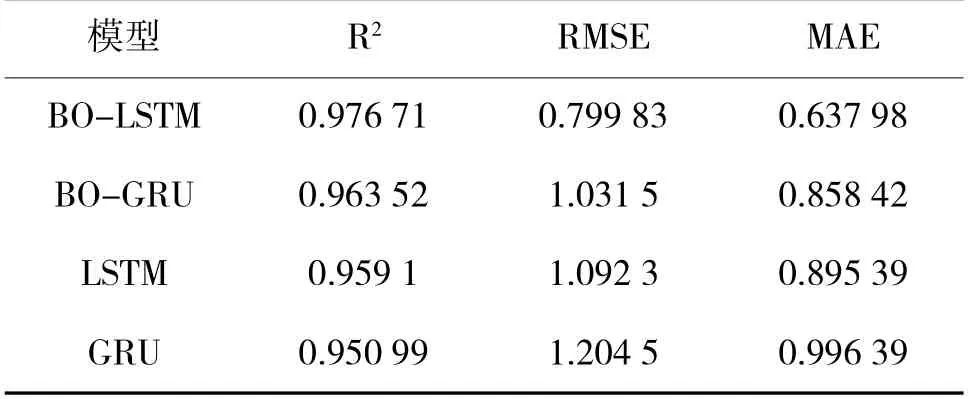
表5 不同预测模型评估结果对比Table 5 Comparison of evaluation results of different prediction models

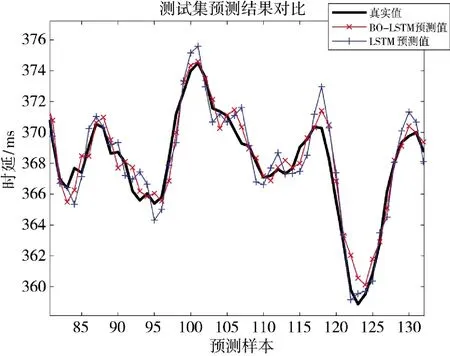
图11 BO-LSTM 和LSTM 预测结果对比Fig.11 Comparison of prediction results between BO-LSTM and LSTM

从图10 的预测结果和表4 中BO_LSTM 和LSTM 模型的决定系数（R2）可以看出，贝叶斯算法优化的LSTM 预测模型在测试集上的预测值，相较于LSTM 预测模型，更贴合测试集实际数据，验证了贝叶斯算法在优化超参数问题的有效性。

为进一步验证贝叶斯算法优化的LSTM 预测模型的有效性，采用了GRU 神经网络，并利用贝叶斯算法优化相同的超参数，将预测结果进行对比，预测结果的对比如图12 所示。

图12 不同模型预测结果Fig.12 Prediction results of different models

GRU 神经网络隐含层的神经元个数gru_hidden_units=21，初始学习速率α=0.009 761 2，正则化参数drop_out=1.027 9e-5。

不同预测模型的评估结果如表5 所示。

由表5 可知，当用决定系数（R2）来评估时，这4种预测模型的R2值都在95%以上，都可以很好地对测试集数据进行拟合，其中，BO-LSTM 预测模型的R2值最高，表明其拟合效果最好，GRU 预测模型的R2值最低，其拟合效果相对较差。

当用均方根误差（RMSE）和平均绝对误差（MAE）来评估时，BO-LSTM 预测模型的RMSE 和MAE 值最小，表明该模型预测精度最高，模型效果最好，GRU 模型的RMSE 和MAE 值最小，表明该模型预测精度最低，模型效果最差。BO-LSTM 模型相较于BO-GRU 模型，RMSE 值减小了22.46%，MAE值减小了25.68%，LSTM 模型相较于GRU 模型，RMSE 值减小了9.32%，MAE 值减小了10.14%，表明了LSTM 模型效果优于GRU 模型。BO-LSTM 模型相较于LSTM 模型，RMSE 值减小了26.78%，MAE 值减小了28.75%，BO-GRU 模型相较于GRU模型，RMSE 值减小了14.36%，MAE 值减小了13.85%，表明贝叶斯算法对模型的优化是有效的。

5 结论

针对通过无线通信网络通信的某地面反无人机系统，分析了系统在工作过程中传输时延的产生与组成，针对网络时延随机变化的特性，提出了一种贝叶斯算法（BO）优化的LSTM 神经网络时延预测模型，将实验测试获得的网络时延数据划分为训练集和测试集，先用训练集训练模型，然后利用训练好的模型在测试集上进行测试，并将预测结果与GRU 和BO-GRU、LSTM 预测方法进行对比，通过对比，BO 优化的LSTM 神经网络时延预测模型预测精度更高，预测效果更好，验证了该预测模型的有效性。