基于Shapley 值的作战体系单元价值评估*

夏庭汉，赵东波，樊 明*，陈清华

（1.北京师范大学系统科学学院，北京 100875；2.解放军32180 部队，北京 100076）

0 引言

随着信息技术的发展，现代战争已经转变为体系与体系的对抗，加快作战体系能力建设已成为当前军队建设的核心任务之一［1］。一般而言，作战体系是为了追求整体效能而构成的复杂军事系统，是由多个作战系统相互协同，按照一定的结构，通过组织、体制、通信及机制连接成一个整体［2］。网络化是其重要的发展方向，核心特征是不同功能网络之间的协同作战，作战系统内部各功能单元通过信息交互建立起作用关系，组成结构复杂的网络系统［3］。在作战体系中，如何快速识别敌方的重要节点进行打击，或调节信息网络结构隐藏并保护己方重要节点，是智能化战争的热点问题［4］。

军事系统中重要节点识别的方法众多，有基于数学解析、统计数据的评估方法，或者基于作战环的评估方法，以及基于复杂网络的评估方法等［5］。其中，基于复杂网络理论与方法针对作战体系的关键结点、脆弱性等关键性问题的研究，或对体系作战效能进行评估［6］尤为受到关注。张剑锋等使用复杂网络方法建立目标价值分析模型，该方法综合考虑了目标节点以及节点间链路的价值，通过网络生成树的数目来度量目标的重要性［7］。李茂林等利用度指标、介数指标、紧密度指标和特征向量指标，对作战网络中的节点重要性进行评估，并结合最大连通分支、平均路径长度以及紧密中心性度量作战网络在遭受攻击后的受损程度，提出了在体系对抗中关键节点的判定方法［8］。邱原等考虑了网络中边的两个端点对边本身的重要性影响，有效克服了以边介数作为重要性指标的片面性［9］。李尔玉等基于作战节点组合后的整体价值，提出一种基于功能链的节点重要性评价方法［10］。张鑫伟等使用熵值法综合几类网络的基本静态指标进行节点重要性判断［11］。荣明通过作战体系弹性仿真实验建立动态超网模型，提出作战体系结构弹性指标对作战体系结构弹性进行分析评估［12］。上述研究从复杂网络的视角研究体系作战以及节点重要性等问题，引入了新的研究方向和研究视角，在现代战争研究领域发挥着越来越重要的作用。但相当多的研究主要是对于复杂网络的相关方法技术的使用，并未充分考虑作战体系的实际特征，对于真实作战体系的分析有待进一步深入。

本文从作战体系的整体功能出发，将由指挥、侦察、战斗、通讯4 种子功能网络构成的作战体系抽象为多路复用网络，在充分考虑网络整体结构以及军事目标特性的基础上，构建了基于Shapley 值的节点价值评估算法，对作战体系网络中军事目标重要性进行评价。该方法也可以结合实际的应用场景进行灵活扩展，具有较好的泛化能力。

1 作战体系网络分析及建模

1.1 作战体系网络结构

体系作战是以交战（物理毁伤与信息对抗）、指控、通信、感知和融合类实体为节点，各实体间的能量、信息和认知交互为边的复杂战争网络，是具有自组织特征的各类网络集成的“网络的网络”。早期对体系作战单层同质网络的建模方法已无法反映信息化条件下体系作战“多网融合”“跨域交互”的特点［13］。面对新的挑战，学者们从不同的角度讨论了作战体系的构成，胡晓峰等从物理域、信息域和认知域的角度出发，按照网络化的组织指挥关系和作战编成将作战体系分成3 层的复杂网络［13-14］。朱涛等将作战体系分解为基础信息栅格、战场感知网格、指挥控制网格和火力打击网格的4 层立体网格［3］。崔琼从指挥信息系统的任务、结构和功能角度，构建了基于任务流的指挥信息系统双层网络模型［15］。伍文峰针对作战体系结构动态演化、受人主导和涉及多域交互等特点，建立了体系协同多层时序网络模型［16］。

结合现代作战体系广泛采用的“侦、控、打、保、评”功能域划分，本文认为作战体系主要是由相互耦合的四重子网络组成，整体结构如图1 所示，分别为通信传输网络、战场感知网络、指挥控制网络和火力打击网络［17］。

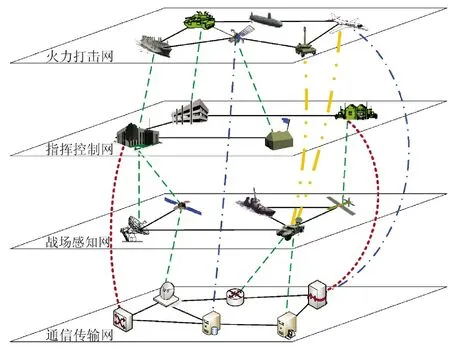
图1 典型作战体系网络结构Fig.1 Network structure of typical combat system

1.2 多路复用网络模型

多层网络已成为网络科学研究的前沿和热点，它突破了单层网络中节点和连边同质性的限制，考虑了多种类型节点及其连边关系（包括层内连边和层间连边）［18］。一个含有M 层的多层网络可以用超邻接矩阵G=（A，O）来表示，其中，表示多层网络中各层的邻接矩阵集合，表示α 层的邻接矩阵，表示α层的节点集合，表示层的层内连边集合，是中的元素：当α 层中节点i 和节点j 有连边时，，否则。表示层间网络的邻接矩阵的集合，元素代表是否存在α 层节点i 到β 层节点j 的连边，和分别表示α 层和β 层的节点集合，表示α 层和β 层的层间连边集合。多路复用网络是一种计算分析更为方便的多层网络，其所有网络层由同一组节点构成。该网络的特点是每一个网络层表示节点间的某种关系或者相互作用模式，而层间连边表示同一个节点在不同网络层的对应关系［19］，如图2 所示。理论上，可以通过在各层网络上增添虚拟的节点和边使得一般的多层网络都能转化为多路复用网络。

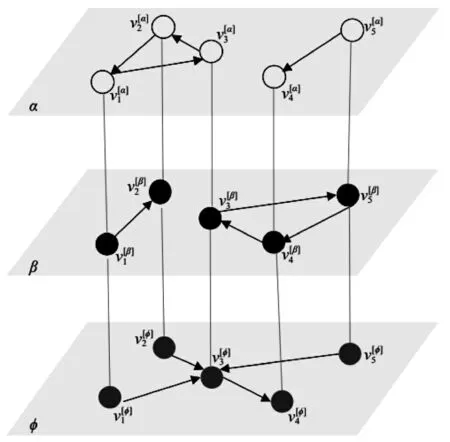
图2 多路复用网络示意图Fig.2 Schematic diagram of multiplex network

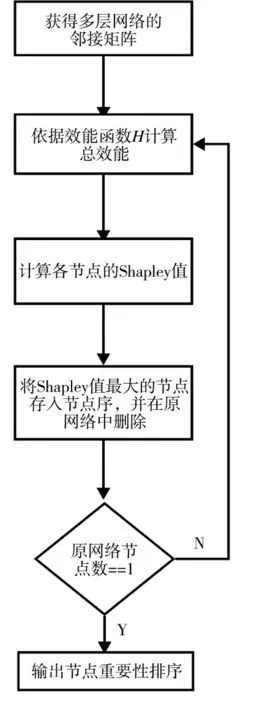
图3 算法流程图Fig.3 Algorithm flow chart

作战体系是一个多维度的系统，具有指挥、通讯、侦察、对抗等一系列的功能，本文假设每个节点都应该具有这4 种功能，只是重要程度不同以及具体表现不同。本文将图1 中一般性的多层网络抽象为一个多路复用网络，其中，跨层的不同节点之间的连接可以将其分解为上层节点在下一层网络的映射，再由该映射连接至目标节点；从功能的角度来理解，对于每个节点，当其需要进行跨层连接时，它需要先进行功能的切换，实现该节点从一层网络到另一层网络的转化，在新的功能层上进行连接。

2 作战单元价值评估算法设计

2.1 多层网络节点重要性评价

复杂网络研究提出了一系列确定节点重要性的方法，它们分别从网络的结构、功能等方面来衡量网络中的重要节点。在军事网络研究领域中，常用的有度中心性、介数中心性，PageRank 中心性等指标［8，11］。而在多层网络中，中心性测度包括节点中心性与层中心性，受到学者的广泛关注，主要介绍两种多层网络节点重要性评价方法。

2.1.1 HD 中心性

文献［20］中用从多路复用网络中提取的对单层网络有效的解来近似多路复用网络上问题的解，提出了基于多路复用网络的节点重要性判断方法HD 和HDA 中心性。HD 中心性利用每层网络上其节点的度值，对每一层该节点的度值进行乘积，获得最终对每个的评分。

基于HD 中心性的思路，将前文所提到的单层网络的中心性指标拓展到多层网络中去，构建了HB（基于多路复用网络的介数中心性指标），HC（基于多路复用网络的集聚系数中心性指标），HE（基于多路复用网络的特征向量中心性指标）等评价指标。

2.1.2 FMP 中心性

在多层网络中，PageRank 节点中心性不仅仅取决于指向该节点的数量和质量，还取决于所在层的相对重要性。文献［21］将其拓展到多路复用网络，提出了functional multiplex PageRank（FMP）方法量化节点中心性，考虑了节点自身和邻居的重要性以及所在层的相对重要性。

2.2 目标价值评价指标构建

一个作战体系的效能是上述多种功能的组合，不同功能的网络之间相互作用，彼此协作。因此，整体的作战效能H 可以表示为基于网络G 的一个函数，也是各个作战单元的效能Hi的总和：

其中，f 表示各层网络和各层网络之间的作用结果，N 为网络中的节点数。在本文后续的讨论中，基于对作战体系的抽象和简化，假设集聚系数中心性能够反映侦察网络的信息收集聚合能力，介数中心性能够反映通讯网络的信息传播能力，特征向量中心性能够确定指挥网络的节点重要性，度中心性能够反映战斗网络的节点重要性。在此基础上，可以得到一个刻画网络整体作战效能的具体指标：

其中，Ei表示节点的特征向量中心性，Bi表示节点的介数中心性，Ci表示节点的局部集聚系数中心性，Di表示节点的度中心性，α1～α4为权重系数。本文通过设定不同的系数来求解体系不同方面的能力，例如若除α2外其他系数均为0，则聚焦分析整体网络中的信息传递的效能。

节点的重要性是指节点对整个体系作战效能的贡献程度，一个节点的重要性不仅在于其直接贡献，也在于其对其体系中其他部分的支持，二者和越大，那么该节点也就越重要。此外，节点重要性不仅取决于对当前结构的贡献，还取决于当体系结构发生变化（如其他单元受损）时对体系的贡献。Shapley 值法通过考虑整个某个节点对于不同组合下的体系整体效能的贡献，综合得到每个节点对于体系的真实贡献。用Shapley 值计算方法如下［22］：

其中，G 为整个网络，|G|表示其中总共的节点数，H表示该子网络的效能，S 表示网络的子网表示S 为网络G 不包含节点i 的任意子网。S∪{i}表示子网S 加上节点i 后构成的新子网。但上述的Shapley 值的计算方法在节点数量较多的情况下，计算复杂，本文使用文献［23］中提出的简化的Shapley值的计算方法以提高计算效率，如下所示：

其中，{vi}∪NG（vi）表示包括节点vi以及它的邻居的集合，wi，j为节点vi和vj之间的权重，当i=j 时，wi，j=1，Hj是vj的节点效能，Dj是vj的度值。

本文依据该多路复用网络每一层对应的功能计算其中心性指标，通过式（3）获得了每个节点的效能。然后对整个网络进行了一次投影，使其成为一个单层网络来确定其节点的邻居，然后计算节点的Shapley 值。

具体的算法流程图如下所示：

3 节点重要性仿真实验

3.1 实验设置

在军事体系对抗中，不同的角色承担着不同功能，对应到网络中即表现为每个节点在不同的网络中均有着不同的地位。实验中使用4 层多路复用网络对作战体系进行抽象。其中的4 个网络具有着不同的结构。研究者们经常使用随机网络（ER），无标度网络（BA），小世界网络（WS）或者规则网络对作战体系进行模拟［3，8-9］，本文通过使用ER、BA、WS网络随机组合，构建不同的多路复用网络进行模拟，如表1 所示。其中，每层网络的节点数都为128 个，平均边密度为0.1，网络内连边数约为820 条。

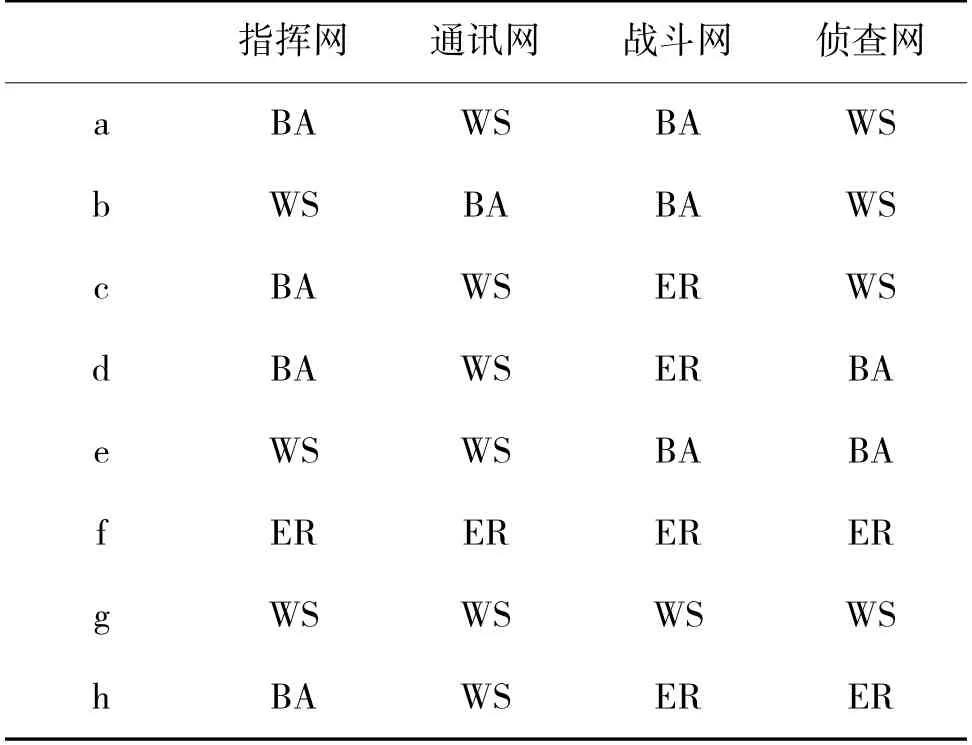
表1 实验的网络构成Table 1 Network configuration of the experiment

3.2 实验结果

基于对网络的设置，本文对该多层网络进行节点删除操作（模拟作战单元受到攻击并损坏的情况），使用不同的方法判断网络的重要节点并对其进行删除，比较网络的整体效能的变化。

从图4 中可以看到，针对不同的网络构成形式，基于传统的节点重要性指标，如介数中心性，集聚系数中心性等并不能稳定且有效对一个多层网络产生有效的破坏，按FMP 法计算节点重要性的方法与使用Shapley 值判断出的节点重要性对网络的杀伤能力相近。

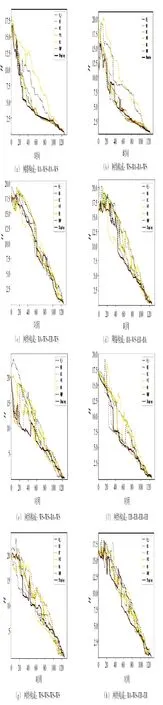
图4 不同攻击情况下的网络效能Fig.4 Network efficiency under different attack conditions

3.3 算法鲁棒性检验

为检验算法的稳定性，以及其对网络结构的泛化能力，基于同样类型的基础网络类型的设置，本文重复100 次实验。结果如图5 所示，箱线图中统计了依据不同方法判断的节点重要性顺序删除节点后，网络整体组织效能曲线所围成的面积大小，面积越小，代表按照该节点重要性顺序删除节点对网络的杀伤能力越强。

图5 不同网络构成下算法鲁棒性检验Fig.5 Robustness test of algorithm under different network configurations

比较发现，Shapley 值的方法具有较高的鲁棒性，在不同网络构成下都有较好表现。

基于上述实验，使用Shapley 值算法对多层网络进行节点重要性的评估，其效果与FMP 算法相近，优于其他从单一中心性指标考虑的方法。从算法的复杂度而言，FMP 算法有着o（n2）的复杂度，而本文提出的基于Shapley 值的作战体系节点价值评估方法，复杂度为o（n），要比前者更有效率。

4 结论

本文在充分考虑网络结构以及军事特性的基础上，构建了重要节点发现的Shapley 值算法，对作战体系中军事目标进行重要性评价，并结合具体算例进行目标价值评估计算验证，显示出较好的性能。利用该算法，可以快速得到作战目标体系中价值较高的关键目标节点，从而支撑决策者进行作战筹划。

本文所提出的基于Shapley 值的方法具有较好的可扩展性，可以根据实际运用场景的需求，对网络结构以及效能函数进行调整并应用于更加复杂的军事系统中；同时，该方法对网络结构的依赖性不强，具有很好的泛化能力，可以应用于其他不同结构的社会复杂系统的评价研究中。该方法的不足是需要对网络结构以及评价指标进行预先的判断与设置，需要的信息量较大，在实际过程中这一条件很难得到满足。后续的工作开展中可结合网络补全等前沿的网络科学方法，基于部分信息对网络结构进行推断，使其具有更加广泛的应用场景。