一种动态不确定海洋环境下的USV 态势自主感知及避障算法

王 潋，陈 霄，完颜娟

（1.解放军91054 部队，北京 102442；2.军事科学院，北京 100091）

0 引言

无人艇作为一种小型的海上无人智能平台，具有高速机动、灵活隐蔽的特点，可潜入敌区，展开情报获取工作，实现对关切海域的持续监视。此外，USV 还可用于反潜、扫雷、电子战、海上搜救、海洋科考、执法取证、后勤支援等军用和民用领域，具有广泛的应用前景［1-3］。在USV 自主执行各项任务过程中，需要实时对其附近海洋环境进行态势感知，收集静态和动态障碍物等信息，来实现对各类障碍物的安全躲避，以此确保所肩负任务的顺利完成［4-5］。

无人艇避障算法种类很多，包括Dijkstra、D*、A*、人工势场法、快速随机搜索树、速度障碍法等［6-9］。周则兴等提出了一种基于改进人工势场法的USV 避障算法，通过引入自衰减斥力场解决了期望航向角突变和抖动的问题，仿真对比结果表明了算法的先进性［10］。张金泽等提出一种密集障碍物海况下的USV 自主避障算法，该算法基于模糊推理的改进型双窗口动态窗口法设计实现，仿真实验表明该算法能有效避免USV 从密集障碍物群外绕行，避障路径更加合理［11］。窦强为解决无人作战艇在未知海域避碰规划问题，借鉴栅格法和人工势场法，设计实现了一种基于导航雷达回波视频的实时避碰规划算法，并通过仿真和实际试验证明了算法是可行的［12］。刘渐道等提出一种融合避碰规则的动态窗口法来解决USV 在海上航行时的自主避障问题，充分考虑开始避障的时机、避让的转向幅度以及何时进行复航等因素，仿真实验验证算法的可行性［13］。

无人艇等水面航行器在实际海洋环境中航行时，主要会受到风、浪、流等不确定因素的影响。通常情况下，为了确保无人艇自身能够按照预定的航线和设定的航速航行，通常分两种情况考虑海洋环境的动态不确定性：一方面无人艇通过装备的风向、风速、海流等传感器，实时感知海洋环境的动态变化，通过航迹跟踪控制算法实时补偿校准，确保无人艇更准确地跟踪航线，主要需要考虑风向、风速、海流等传感器的测量误差；另一方面无人艇通过搭载的雷达等传感器，实时感知周围障碍物的情况，预测动态障碍物的运动轨迹，以在合适的时间启动恰当的避障算法，实现对障碍物的准确躲避，主要需要考虑雷达等传感器测量误差、观测漂移和动态障碍物随机运动不确定性。本文主要研究USV态势自主感知及避障算法，因此，考虑采用已经对风向、风速、海流等传感器的测量误差进行了补偿校准的航迹跟踪控制算法，例如文献［14］中的算法，主要考虑传感器测量误差、观测漂移和动态障碍物随机运动不确定性这一类因素。

本文针对USV 在动态不确定海洋环境下的态势自主感知和实时避障问题，充分考虑传感器测量误差、观测漂移和动态障碍物随机运动不确定性，对相关误差进行不确定性建模，设计了一种融合COLREGs 海事规则的USV 态势自主感知及避障算法，给出了算法详细的流程设计图，并通过正面相遇、追越、左右交叉相遇4 种典型的场景，对本文提出的算法进行了仿真实验验证，仿真结果表明了本文所提出的考虑COLREGs 规则和动态不确定海洋环境下的USV 态势自主感知及避障算法的有效性。

1 三类海事规则

如图1 所示，以USV 航向为基准，定义追越、交叉相遇和正面相遇3 个场景。追越：若USV 与障碍物的航向差在［0°，45°）和［315°，360°）区间，若有碰撞威胁，USV 须从障碍物左侧通过。交叉相遇：若USV 与障碍物航向差在［45°，165°］区间，若有碰撞威胁，USV 须左侧航行躲避；若差值在（195°，315°）区间，若有碰撞威胁，USV 须右侧航行躲避。正面相遇：若USV 与障碍物的航向角度差值在（165°，195°］区间，若有碰撞威胁，USV 须右侧航行躲避。

图1 冲突场景定义Fig.1 The definitions of conflict scenes

2 融合COLREGs 规则的速度障碍法

定义使用COLREGs 规则的时机是十分困难的，当前学术界和工业界均没有精确标准，本文采用判定距离L0，以此来触发COLREGs 规则的启用时机。具体如下：若USV 与障碍物之间的距离大于L0，则不进行避让；若USV 与障碍物之间的距离小于L0，当存在碰撞危险时，则遵循COLREGs 规则启用局部动态路径规划，USV 局部动态路径规划采用融入COLREGs 规则的速度避障法。

如下页图2 所示，假设障碍物为圆形并进行适度膨胀（非圆形可采用其外接圆表示），USV 相对于障碍物的速度为V=VA-VB，以USV 的位置为顶点，向障碍物作切线l1，l2，定义两切线间为锥形碰撞区并记为VO，即V 处于两切线之间时，必会碰撞。对于多个障碍物，VO 域记为多个障碍物计算后VOi的集合，即，m 为障碍物的个数。当USV 的速度矢量与VO 域有重叠部分且距离小于等于L0时，USV 立即改变航向或速度以脱离碰撞区。

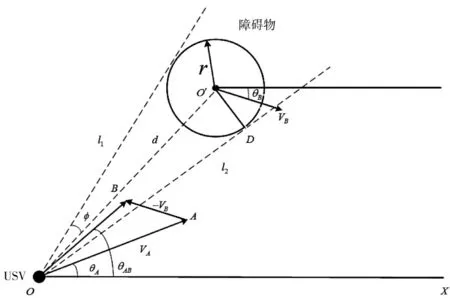
图2 速度障碍法Fig.2 Velocity obstacle avoidance algrithm

以障碍物在USV 的左侧为例，假定t=i 时刻，已知障碍物的速度为VB，航向为θB，USV 的速度为VA，航向为θA，障碍物的半径为r，其与USV 之间的距离为d，且与USV 的连线OO'与X 轴之间的夹角为α，则，。根据余弦定理可得：

1）对于执行精确循迹任务的USV 和转向困难或转向代价较大的大型USV，在探测到未知障碍物时，可只改变航速，不改变航向。首先，求解相撞时的速度，其中，d 为USV 与障碍物间的距离，可通过传感器获取，T 为时间周期。之后，根据避障要求确定速度的改变量。若要求以避障最短时间为首要目标，则，dmin最小安全距离；若以安全为首要保证，则，dmax为最大安全距离。

2）根据COLREGs 规则，改变USV 的航向，可分为USV 航向、航速均改变和仅改变USV 航向两种情况，需要根据其与障碍物的相遇场景来选定，具体设计如下：当USV 与障碍物相遇场景为“追越”时，在根据COLREGs 规则改变USV 航向的同时，USV 的期望速度设计为原期望航速的1.5 倍；当USV 与障碍物相遇场景为“交叉”时，在根据COLREGs 规则改变USV 航向的同时，USV 的期望速度设计为原期望航速的0.5 倍；当USV 与障碍物相遇场景为“正面相遇”时，USV 的期望速度设计为原期望航速的0.5 倍。

避障结束后，USV 根据自身所在的位置和原全局路径规划的航线信息，在恰当的跟踪控制算法的作用下，恢复到原航线上，继续自主航行。

3 信息的不确定性建模

由于USV 航行在复杂时变的海洋环境中，障碍物运动具有一定的不确定性，且USV 航行中对障碍物位置和运动的探测都依靠各类传感器，如雷达、测速仪等，无法避免地存在测量误差或漂移等问题。因此，在USV 态势自主感知及避障过程中，须对传感器测量误差和障碍物随机运动导致的不确定性进行建模。

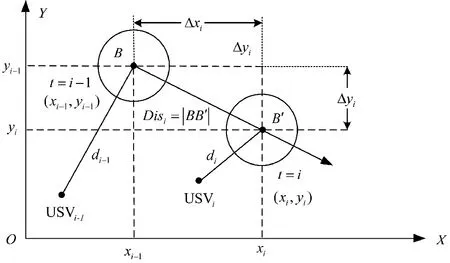
图3 不同时刻的障碍物位置Fig.3 The obstacle location at different times

式中，θ 为待估计的参数，Θ 为其取值范围。假设X的样本值为，则的联合分布率为。设定的样本值为，则事件发生的概率为：

极大似然函数为：

由式（8）解得：

由此可得μ，σ2的极大似然估计量分别为：

同理，应用极大似然法估计Δv 和Δθ 的期望和方差：

在正态分布中，根据“3σ”法则约有99.7%的值分布在均值μ 附近3 个标准差σ 的区域内。

4 考虑不确定信息的USV 态势自主感知及避障算法

如下页图4 所示，在t=i 时，根据t=1，2，…，i-1时刻障碍物的状态，对t=i 时刻障碍物的速度矢量建模，并利用第3 章中的方法估计出t=i 时刻的由此求得t=i 时的和。根据“3σ”法则，t=i 时和的大小分别在区间内。障碍物速度矢量变化最大时，不确定性最高，据此确定其二次膨胀半径R，从而将不确定性转化为确定性。此外，由图4 中几何关系可得：

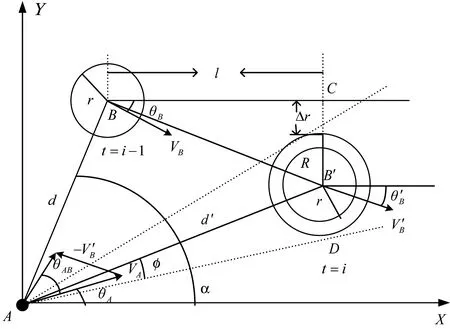
图4 考虑障碍物不确定性的情况Fig.4 The situation considering uncertain information about obstacles

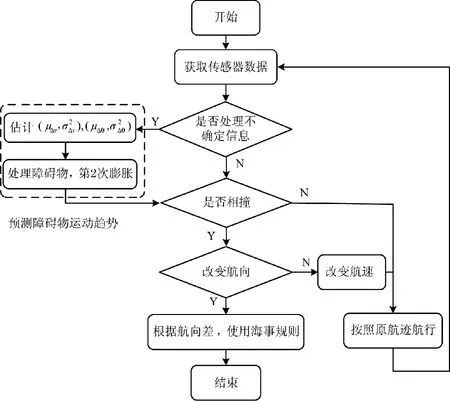
图5 考虑COLREGs 规则和不确定性信息的USV 局部路径规划流程图Fig.5 The local path planing flow chart of USV considering COLREGs rules and uncertain information

5 仿真实验与分析

考虑USV 在沿全局路径航行时对未知动态和静态障碍物的避障问题，如图6 所示，红色区域为已知的静态障碍物，为模拟动态障碍物运动的不确定性，其速度变化量为Δv=0.2 kn，变化范围为［-2，2］kn；角度变化量设置为Δθ=2°，变化范围为［-15°，15°］，在t=i 时，根据t=1，2，…，i-1 时刻障碍物的运动状态，利用第3 章中的方法估计出t=i 时刻的，由此求得t=i 时的和。根据“3σ”法则确定障碍物的二次膨胀半径。取判定距离L0=80 m，最小和最大安全距离为dmin=20 m，dmax=80 m。本章分4 种典型的相遇场景进行仿真实验。

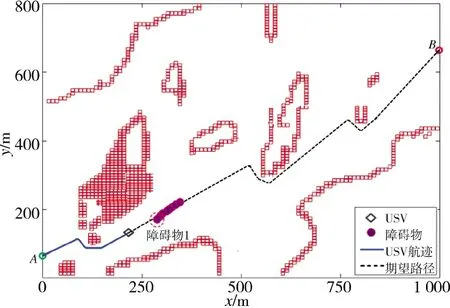
图6 USV 与障碍物正面相遇Fig.6 USV encountering the obstacle face to face

5.1 正面相遇和追越场景

障碍物设置如下：

障碍物1：起始点位置坐标（350，210），航速为10 kn，航向为220°，t=10 s 时，障碍物开始运动；

障碍物2：起始点位置坐标（850，500），航速为6 kn，航向为35°，t=85 s 时，障碍物开始运动。

USV 的初始航速仍设定为20 kn，全局路径起始点为A，终止点为B，从图6 可以看出，USV 通过对障碍物一段时间内（本节仿真中从障碍物开始运动时刻开始计算）运动不确定性航向、航速数据进行不确定性建模，得到膨胀半径，据此对障碍物进行二次膨胀，如图6 中红色虚线圆所示。

当USV 距离障碍物1 80 m 时，USV 判定会遇场景为正面相遇，并立即开始进行局部路径规划进行自主避障，依据COLREGs 规则，USV 从被超越障碍物的右舷处航行通过。如下页图7 所示，可以看到USV 在障碍物的右侧规划出了一条局部避障路径，并在航迹跟踪控制算法的作用下，通过跟踪规划好的局部路径，实现了对障碍物的右舷超越，之后USV 能够继续沿任务之初规划好的全局路径航行。

图7 正面相遇下USV 自主避障Fig.7 The autonomous obstacle avoidance of USV in head-on encounter

USV 在沿全局路径航行过程中，实时检测未知障碍物，如图8 所示，当USV 距离障碍物2 80 m时，USV 判定会遇场景为追越并开始进行局部路径规划，依据COLREGs 规则，当存在碰撞危险时，要求USV 从被超越障碍物的左舷处安全通过，如图9所示，可以看到USV 在障碍物的左舷规划出了一条局部避障路径，并在航迹跟踪控制算法的作用下，通过跟踪规划好的局部路径，实现了对障碍物的左舷超越，之后USV 能够继续沿任务之初规划好的全局路径航行。

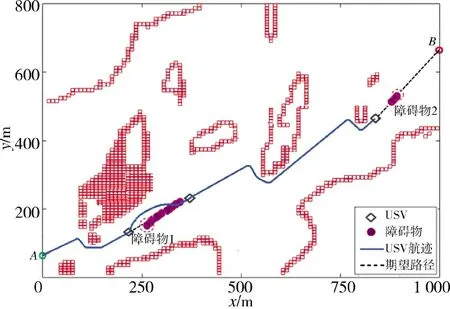
图8 USV 与障碍物追越场景仿真图Fig.8 The overtaking scene simulation diagraph between USV and the obstacle

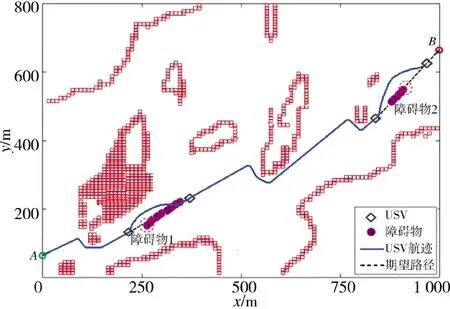
图9 追越场景下USV 自主避障Fig.9 The autonomous obstacle avoidance of USV under overtaking scene

5.2 左右交叉相遇场景

障碍物设置如下：

障碍物3：起始点位置坐标（295，375），航速为15 kn，航向为145°，t=20 s 时，障碍物开始运动；

障碍物4：起始点位置坐标（750，305），航速为12 kn，航向为325°，t=60 s 时，障碍物开始运动。

同样地，USV 全局路径的起始点为A，终止点为B，初始航速仍设定为20 kn，从图10 可以看出，USV 通过对障碍物一段时间内运动不确定性航向、航速数据进行不确定性建模，得到膨胀半径，据此对障碍物进行二次膨胀，如图10 中红色虚线圆所示。

图10 USV 与障碍物左交叉相遇场景仿真图Fig.10 The left cross encounter scene simulation diagraph between USV and obstacle

当USV 距离障碍物3 80 m 时，USV 判定会遇场景为左交叉相遇并开始进行局部路径规划，依据COLREGs 规则，当存在碰撞危险时，要求USV 左侧航行躲避。如图11 所示，可以看到USV 在原航行路线的左侧规划出了一条局部避障路径，并在航迹跟踪控制算法的作用下，通过实时跟踪规划好的局部路径，实现了对障碍物的有效躲避，之后USV 能够继续沿任务之初规划好的全局路径航行，并实时检测未知障碍物。

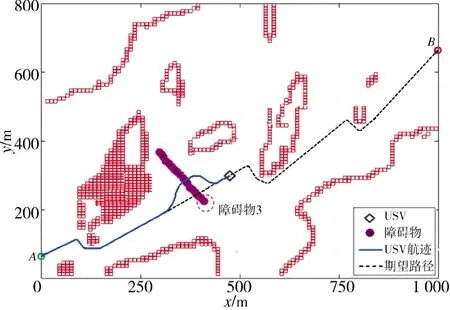
图11 左交叉场景下USV 自主避障Fig.11 The autonomous obstacle avoidance of USV under left cross scene

如图12 所示，当USV 距离障碍物4 80 m 时，USV 判定会遇场景为右交叉相遇并开始进行局部路径规划，依据COLREGs 规则，当存在碰撞危险时，要求USV 右侧航行躲避，如图13 所示，可以看到USV 在原航行路线的右侧规划出了一条局部避障路径，并在航迹跟踪控制算法的作用下，通过实时跟踪规划好的局部路径，实现了对障碍物的有效躲避，之后USV 能够继续沿任务之初规划好的全局路径航行，并实时检测未知障碍物，直至安全到达全局路径的终点。仿真结果表明了本文所提出的考虑COLREGs 规则和动态不确定海洋环境下的USV态势自主感知及避障算法的有效性。

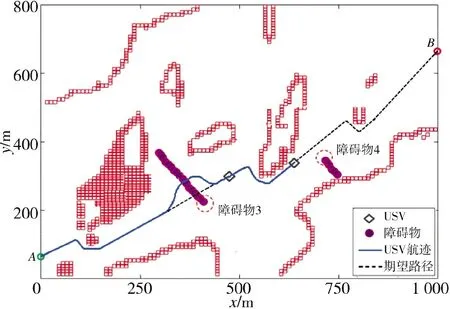
图12 USV 与障碍物右交叉相遇场景仿真图Fig.12 The right cross encounter scene simulation diagraph between USV and the obstacle

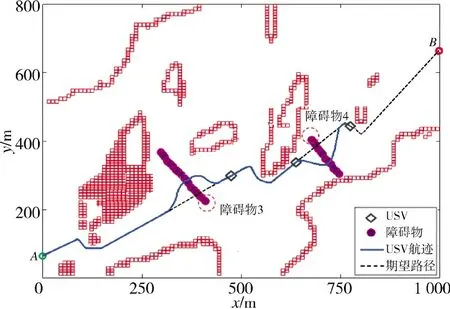
图13 右交叉场景下USV 自主避障Fig.13 The autonomous obstacle avoidance of USV under right cross scene

6 结论

本文针对USV 在动态不确定海洋环境下的态势自主感知和实时避障问题，设计了一种融合COLREGs 海事规则的USV 态势自主感知及避障算法，该算法充分考虑了传感器测量误差和障碍物随机运动不确定性，对相关误差进行不确定性建模，并通过正面相遇、追越、左右交叉相遇4 种典型的场景进行仿真实验证明了算法的先进性和有效性。

本文提出的算法融合了真实的海上航行规则，且拥有较强的稳定性和较低的计算量，在工程实践中具备很好的指导意义。与此同时，对我国USV 相关航行避障技术和相关避障系统等装备的研制具有一定的理论指导和现实意义。