基于深度学习的MIMO 雷达一体化处理*

姜春磊，陈宝欣，黄 勇

（1.烟台黄金职业学院，山东 招远 265401；2.解放军92337 部队，辽宁 大连 116085；3.海军航空大学，山东 烟台 264000）

0 引言

相干雷达系统中一般采用波束形成、脉冲压缩、相参积累（杂波抑制）、目标检测和目标跟踪识别的级联信号处理方式。相互级联的各个处理流程之间会相互影响，即前面处理结果的好坏会直接影响后面的处理结果。然而，一般在雷达信号处理研究中都作了简化处理，默认假设前面的信号处理结果是完美的。并且，各个处理流程对应的各种方法都有相应的模型假设。这种传统的处理方式可以概括为基于模型驱动的级联处理，且一般需要两类假设。第1 类是信号模型假设，即需要确知的信号波形和特定的目标（运动）类型。比如，脉冲压缩技术利用大时宽- 带宽积信号可以同时提高检测性能和距离分辨率。匹配滤波是最常用的脉冲压缩方法，在点目标和白噪声假设条件下可以获得最大输出信噪比。然而，当采样失配、目标距离扩展时，常规的匹配滤波的性能将下降，且距离旁瓣会增强。因此，在实际中，多采用加窗处理以抑制旁瓣水平。此外，基于失配滤波的方法被提出以解决距离旁瓣和由目标多普勒造成的失配问题。第2 类是环境模型假设，即需要假设背景的分布类型、分布特性以及干扰目标数量等信息。比如，在基于模型驱动的级联处理流程中，目标检测一般位于脉冲压缩之后。如果干扰目标旁瓣未得到有效解决，势必会影响后续的检测效果。一个较为常见的情况是，由于受大目标旁瓣的影响，大目标附近的小目标难以被检测。另一方面，雷达目标检测最常用的方法是基于奈曼—皮尔逊（neyman-pearson，NP）准则的恒虚警（constant false alarm ratio，CFAR）检测器。在过去的几十年里，CFAR 技术得到了长足的发展。然而，各种CFAR 检测器存在的一个缺陷是：在使用这些方法时必须满足对应的背景模型假设，如CA-CFAR 假设参考窗内的和检测单元的所有干扰数据样本是独立同分布的；OS-CFAR 需要满足参考单元的干扰目标数小于2n-k 的条件，且其余单元数据独立同分布。CFAR 技术也难以综合考虑目标旁瓣、多普勒失配和多目标等情况同时存在时的检测问题。因此，在实际应用过程中，虚警概率与检测概率的平衡需要在整个系统级层面考虑，即在检测前通过脉冲压缩、MTI、STAP 等提高信杂（噪）比和在检测后通过多次的扫描判断降低虚警。对于MIMO 雷达而言，非理想正交波形会导致上述问题更加严重。

近年来，以深度学习为代表的人工智能方法在图像识别等计算机视觉领域的巨大成功，极大地促进了其在各个领域的应用。深度学习通过构建深度神经网络（neural network，NN）在海量数据样本中逐层抽象挖掘有用信息，极大减轻了对模型假设的依赖。在雷达领域，深度学习的一个直接应用是检测SAR 或其他雷达图像中的目标［1-3］。由于目标检测的本质是一个二分类或多分类问题，因此，对于序列形式的雷达信号而言，神经网络也可以用来近似雷达目标检测器。文献［4-8］分别利用神经网络实现了杂波中的雷达目标检测。PRASHANT 等实现了神经网络在非高斯噪声中的信号检测［9］。CAI 和ZHANG 等采用时频分布作为神经网络的输入实现了检测的过程［10-11］。WANG 等将距离-多普勒谱看作图像输入，采用卷积神经网络实现了目标检测［12］。早期的研究证明了采用均方误差的神经网络可以用来近似贝叶斯最优判别函数和奈曼- 皮尔逊检测器［13］。MARíA-PILAR 等对此做了大量研究［7-8］。在使用神经网络近似NP 检测器时，训练时的误差函数是确定神经网络检测器逼近性能的关键参数。文献［14］证明了使用MSE 或交叉熵作为损失函数的神经网络检测器对所有可能的Pfa 是最优的。此外，还有通过神经网络判断背景类型以选择采用CACFAR 还是OS-CFAR［15］，或者通过CA-CFAR 或GO-CFAR 来监督神经网路的训练，以保证在达到相应CFAR 检测概率的前提下降低虚警率［16］。然而，上述神经网络在雷达中的研究前提一般是基于理想的脉压后信号，没有综合考虑多普勒频移、脉压旁瓣以及多目标对检测结果的影响，而这些因素在实际中是难以避免的。根据神经网络的万能近似定理，一个具有线性输出层和至少一个具有挤压式激活函数作为隐层的前馈神经网络，可以以任意非零误差逼近从一个有限维空间到另一个有限维空间的连续波莱尔（borel）可测函数［17］。因此，理论上讲，可以实现脉冲压缩、相参积累（杂波抑制）和目标检测的一体化处理，从而降低对各种模型假设的要求，也即信号处理的方式由模型驱动转换到数据驱动。

当前深度学习在MIMO 雷达领域的主要应用包括：人体运动特征分析、人体姿态识别、跌倒检测与保健检测、自动驾驶等［18-21］，当前的研究多是采用将预处理的频谱图像作为深度神经网络的输入，本文提出基于深度学习的MIMO 雷达多维目标检测框架，通过构建三维卷积神经网络（convolutional neural network，CNN）检测模型，直接在接收端检测发射波形，实现空域、时域和距离维的联合处理。

1 离散信号模型与问题描述

考虑一MIMO 雷达系统，包含NT个发射阵元和NR个接收阵元，令

表示从第n 个阵元发射的长度为NW的信号。则

为全部发射信号。进一步，令

其中，L 表示感兴趣的距离单元数。对于发射NP个相干脉冲的MIMO 雷达，接收的第p 个脉冲可表示为：

其中，α（l，θ）为第l 个距离单元、角度θ 处目标的复散射系数，fd为目标归一化数字多普勒频率，a（θ）和b（θ）分别为发射和接收导向矢量，定义为

将来自NP个脉冲的所有信号表示成三阶张量的形式

式（8）所示的三阶张量模型也是一般阵列雷达的推广形式，传统的信号处理流程包括波束形成、脉冲压缩、杂波抑制和目标检测。前三者的本质都是基于相关原理实现对期望信号的相参积累，并抑制非相干信号，或者可以看作是一种变换的过程，即将信号从一种域变换到另一种紧凑或抽象的表征域中，如傅里叶变换、分数阶傅里叶变换等，这些变换的最终目的是为了更容易地实现分类（检测），而任何分类器（检测器）的性能必然会受到之前变换方法的影响。深度学习为这个问题带来不同的解决方案，不仅可以学习分类器（检测器），还可以直接从数据中学习所需要的变换。

2 基于三维卷积神经网络的MIMO 雷达一体化处理

本章构建基于深度学习的多维目标检测框架，利用相关原理与卷积神经网络的相似性，搭建了基于深度三维卷积神经网络的多维一体化处理模型。

2.1 基于三维卷积神经网络的MIMO 雷达多维目标检测模型构建

卷积神经网络是一种特殊的神经网络，由于其局部分层抽象表示的能力，在计算机视觉等领域取得了巨大的成功。卷积神经网络成功的关键设计思想有两点：1）卷积神经网络充分利用了图像的二维结构，而图像上相邻像素之间一般都是高度相关的。此外卷积结构依赖于特征共享，因此，每个通道是由相同的卷积核卷积得到的，这个结构使得卷积神经网络的参数量大大降低。2）卷积神经网络通过引入池化的步骤，使得网络结构对位置偏移具有稳健性。同时，池化还允许网络随着深度的增加上获得更大的视野。例如，在图像目标识别的过程中，卷积层逐层聚焦物体的边缘、部分和整体。这两点与基于相关原理雷达信号处理有很多相似性，如不同阵元、不同脉冲、不同快时间采样的目标信号之间一般也是高度相关的，卷积核与输入互相卷积的本质仍是相关操作，池化层的作用类似于稳健波束形成的作用。此外，深度神经网络强大的非线性映射能力为检测具有更复杂特性的目标提供了可能性，因此，可以利用深度三维卷积神经网络实现多维联合目标检测。

基于深度三维卷积神经网络的MIMO 雷达多维目标检测模型如下页图1 所示，输入为接收的三阶张量。由于雷达接收的信号一般是经过IQ 正交采样的复信号，而一般神经网络只能处理实数，所以需要将输入拆分为实部和虚部两部分，即输入层的维度为。

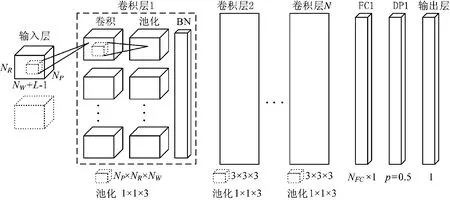
图1 基于深度三维卷积神经网络的MIMO 雷达多维目标检测模型Fig.1 MIMO radar multi-dimensional target detection model based on deep 3D convolutional neural network

隐含层包含多个卷积层、一个全连接层和一个Dropout 层，下面分别介绍各层的具体配置：

1）卷积层

每个卷积层由3 种运算构成，即卷积、池化和批归一化运算。三维卷积神经网络相对于二维卷积神经网络增加了一维深度信息，其卷积核是一个三阶张量。三维卷积的过程如图2 所示，图中卷积核维度为2×2×2×1（第四维为通道），与输入张量内积得到卷积输出，卷积的计算如式（9）所示。

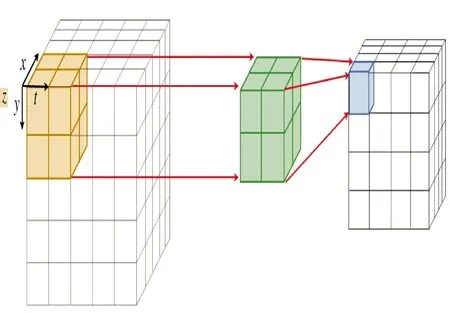
图2 三维卷积Fig.2 Three dimensional convolution

其中，ol，m，n为在l，m，n 处的特征映射，f 为激活函数，wi，j，k为卷积核权重，为前一层的输入值。卷积层1 与输入层采用硬连接（hardwired）的方式，卷积核大小为NP×NR×NW×N1，其中，N1表示第1 层卷积核的数量。其余卷积层的卷积核都为3×3×3，以降低计算量和参数量。

每个卷积运算后是池化运算，池化运算本质是一个降采样的操作，仿照的是人类视觉对输入降维和抽象的过程。池化的主要功能是保证特征不变形，降低特征维度，并具有防止过拟合的功能。常用的池化运算有最大池化和平均池化两种。

每个卷积层的最后一个运算是批标准化（batch normalization，BN）运算，批标准化是近年来深度学习领域的重要成果，很多成熟的网络结构中都有应用。批标准化来源于图像白化操作，早期的计算机视觉领域研究表明对输入图像进行白化操作可以加快收敛速度。在深度神经网络中，随着网络的加深，每一层输入的分布在发生偏移，激活函数常常工作在取值区间的极限饱和区，导致梯度消失，收敛变慢。因此，如果在神经网络的每一层都做归一化处理，那么也可以加快训练收敛过程。批标准化运算一般伴随小批量随机梯度下降方法（mini-batch SGD），计算过程如下

其中，NB为每个小批次的数据量，参数γ 和β 分别为尺度变换和平移变换参数，在训练的过程中更新，用于将变换后的数据再反变换回激活函数的非线性区间，其作用是平衡输入到输出的线性与非线性程度。xi是批标准化的输入，其既可以是激活函数后的输出，也可以是激活函数之前的线性变换结果。

2）全连接层与Dropout

将最后一个卷积层的输出平铺成NFC×1 的一维向量后连接至全连接层，全连接层再与同维度的Dropout 层连接。Dropout 层的作用同样是为了防止过拟合，其基本原理是通过一定的概率p 随机抑制一部分神经元的输出，使每次训练的网络结构不同，这相当于对多个不同的神经网络取平均。由于不同的网络会产生不同程度的过拟合，这样多个网络的平均会在整体上减少过拟合。

输出层大小为LNS×1 的向量，即对应感兴趣的L 个距离单元和NS 个空域单元。此时的问题就转化为机器学习里的多标签分类问题，由于输出单元较多不便于分析模型的检测概率和虚警概率，本文假设每个角度-距离单元只有一个目标，输出层仅考虑一个待检测的角度—距离单元，即取L=NW，待检测单元为第NW个距离单元。

2.2 深度神经网络的训练策略和检验输出

本文采用交叉熵作为损失函数，由于目标在观测空间中一般是非常稀疏的，有目标的数据相对于无目标的数据要少得多，即训练数据不平衡。数据不平衡会导致训练结果虽然准确率很高，但是精确率很低，甚至可能会发生神经网络的预测全部趋向于0。为此，采用加权交叉熵损失函数，如下

其中，α 为加权系数。有目标的数据少，则取α＞1。根据文献［14］中关于神经网络满足奈曼皮尔逊准则的充分条件可得

3 仿真与分析

本章通过仿真构建MIMO 雷达数据集用于模型训练和评估，MIMO 雷达仿真参数如表1 所示。最多30 个干扰目标均匀分布于-30°～30°和0～39 号距离单元内，目标信噪比变化范围为-40～40 dB，待检测单元为第20 号距离单元和第31 号角度单元。

表1 MIMO 雷达系统参数Table 1 MIMO radar system parameters

3.1 超参数对模型训练的影响

基于三维卷积神经网络的MIMO 雷达检测器含有较多超参数，如网络层数、卷积核数量、卷积层输出维度、Droupout 概率值和损失函数加权系数等，其中比较重要的是交叉熵损失函数的加权系数α，这里仅给出不同α 时的网络训练和验证损失函数曲线，如图3 所示。由图可知，α 过小时，模型可以很快收敛，但此时的训练和验证损失都比较大，这是由于严重的数据不平衡问题导致网络输出结果倾向于样本数量较多的类别，合理的加权值通过放大小样本类别的损失，可以缓解不平衡样本的训练问题。

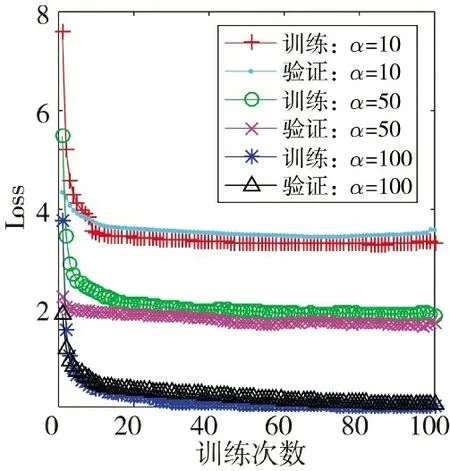
图3 不同α 值的训练与验证损失Fig.3 Training and validation losses for different values of α

3.2 检测性能分析

通过ROC 曲线对比分析基于常规脉冲压缩、波束形成、相参积累和目标检测级联处理的方案与基于三维卷积神经网络的MIMO 雷达一体化处理的方案，其中，级联方案的检测器采用单元平均恒虚警检测器，参考单元和保护单元数分别为16 和2。待检测目标位于第20 个距离单元，归一化空间频率和多普勒频率都为0，信号信噪比定义为相对于全相参积累的信噪比增益。

3.2.1 单目标环境

首先考虑单目标时的性能差异，两种处理方案ROC 曲线结果如图4 所示。在单目标环境下，常规级联处理的单元平均恒虚警检测器仍可看作是最优检测器，此时基于深度学习的检测器与级联处理的检测结果相差不大。

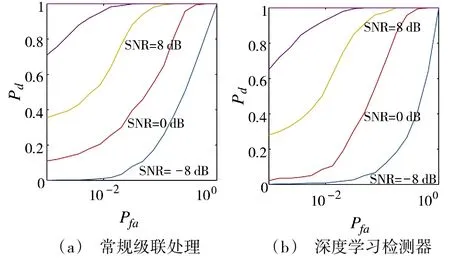
图4 单目标时两种处理方案的ROC 曲线Fig.4 ROC curves of two processing schemes for one single target

3.2.2 邻近角度单元干扰目标

考虑邻近角度单元有一干扰目标，干扰目标的距离与待检测目标相同，角度为5°，多普勒频率为0。两种处理方案的性能曲线如图5 所示，由于干扰目标角度和距离旁瓣的影响，两种处理方案的检测性能都开始下降，但是深度学习检测器要明显优于常规级联处理。

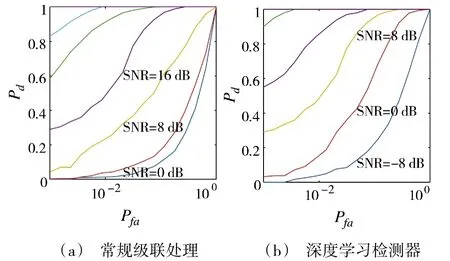
图5 邻近角度单元目标干扰时的ROC 曲线Fig.5 ROC curves when adjacent angle cells exist interference targets

3.2.3 邻近角度单元随机干扰目标

考虑邻近干扰目标的角度在-30°～30°随机变化，且不等于0°，干扰目标的距离与待检测目标相同，多普勒频率为0。两种处理方案的性能曲线如图6 所示，常规级联处理的性能严重下降，深度学习检测器虽也有下降，但是要显著优于前者。

图6 干扰目标角度随机时的ROC 曲线Fig.6 ROC curves when interference targets angles are random

如果干扰目标角度、距离、多普勒、数量、强度和杂波等因素都随机变化时，常规基于模型驱动的级联处理方案的性能将进一步下降，基于深度学习的多维数据驱动方案，为应对这种复杂情况提供了新的解决思路，可以在一定程度上降低对各种模型假设的要求。在实时性方面，尽管深度学习方法提供了一种革命性的数据驱动方法，但这些方法具有显著的计算复杂性。为便于统计分析深度学习方法与传统方法的性能，本文在仿真中作了适当的限定，如阵元数量、脉冲数量、目标范围等。近年来，由于功能强大的图形处理单元（GPU）和张量处理器（TPU）的可用性，这些方法的实现成为可能，神经网络可利用其内部的计算提高训练和预测的实时性。由于涉及的影响因素众多，难以全面比较分析，本文仅是从仿真的角度，验证了深度学习对MIMO 雷达多维一体化处理的可行性和有效性，后续研究应该从更高效的网络结构和与传统方法相结合等角度考虑。

4 结论

传统基于模型驱动的级联处理方法对模型假设依赖严重，如果数据与假设模型不符，则处理性将下降，为此，本文引入了基于深度学习的数据驱动的方法，实现了MIMO 雷达多维一体化处理。构建了基于三维卷积神经网络的MIMO 雷达多维一体化处理架构，并评估了一体化处理相对于级联处理的性能。实验结果表明基于深度学习的多维一体化处理的有效性。