解题需要重视寻找“切入点”

云南省曲靖市民族中学 (655000) 杨丽琼

学习数学需要解题,而解题方向是否合理,解题过程的繁冗与简捷,往往在于解题“切入点”的选择.善于从题目所显示的或隐含的某些特点中寻找解题“切入点”,既能快速决策解题的方向,也能优化解题的过程,起到“四两拨千斤”的解题效果.本文从几个方面阐述寻找“切入点”的途径.

1 从特殊数值寻找“切入点”

在数学题目中,往往出现具有某种特点的一些数值,这些数值对解题有着重要的导向作用.从这些特殊数值上展开联想,进而顺藤摸瓜寻找解题“切入点”,则能获取新颖、独到的解法.

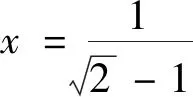
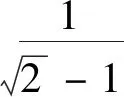
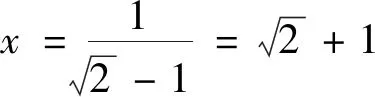
2 从图形背景寻找“切入点”

对于许多数量关系的题目,若挖掘并运用蕴含在题目中的图形背景,使得数量关系转换为直观图形来解决,从图形背景中寻找“切入点”,则解题思路直观、清晰.

例2 (1987年全国初中数学联赛题)已知方程|x|=ax+1有一个负根而且没有正根,那么a的取值范围是( ).

A.a>-1 B.a=-1

C.a≥1 D.非上述答案

分析:本题若按常规方法来解,需要分为两个步骤来进行:①先设x为方程负根,推出a的范围;②根据方程没有正根求a的范围时,正难则反,先假设方程有一个正根x,得到a的范围后取其反面.进而综合后得到答案.所以运用常规思路解答逻辑推理要求高,而利用图形背景,设出函数并作图象,借助图象化“数”为“形”,则求解直观、迅速.

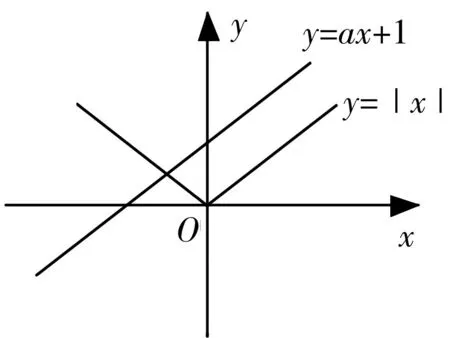
图1

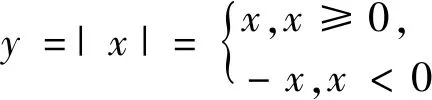
3 从位置关系寻找“切入点”

许多与图形相关联的题目都具有一些特定的“位置”,从与众不同的位置关系中去寻找解题的“切入点”,可快速明确解题方向,利用解题.

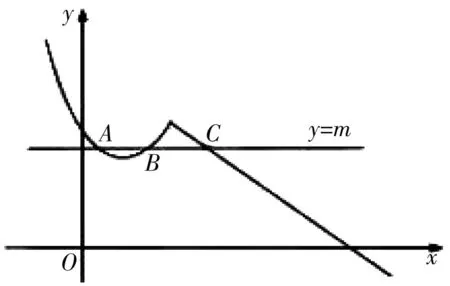
图2

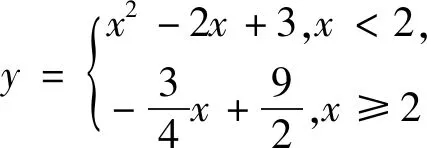
4 从式子结构寻找“切入点”

许多题目中式子的结构具有“窗口”作用,善于对式子结构的观察、分析,从式子结构中寻找解题“切入点”,则解题往往做到事半功倍.

例4 (2019年全国初中数学竞赛天津赛区初赛题)若四个互不相等的正实数a,b,c,d满足(a2012-c2012)(a2012-d2012)=2012,(b2012-c2012)(b2012-d2012)=2012,则(ab)2012-(cd)2012的值为( ).

A.-2012 B.-2011 C.2012 D.2011

分析:由已知条件可知,a2012与b2012满足相同的结构形式,因此构造方程(x-c2012)(x-d2012)=2012,整理后利用韦达定理求解.

解:因为(a2012-c2012)(a2012-d2012=2012,(b2012-c2012)(b2012-d2012)=2012,所以a2012与b2012是方程(x-c2012)(x-d2012)=2012,即x2-(c2012+d2012+(cd)2012-2012=0的两根.根据韦达定理,得a2012·b2012=(cd)2012-2012,即(ab)2012=(cd)2012-2012,所以(ab)2012-(cd)2012=-2012.故选A.

5 从整体关系寻找“切入点”

在解决一些题目中,若把某些具有一定关系的式子视为一个整体,以此为解题“切入点”,则往往使题目得到迅速解决.

分析:若先求解已知中的一元二次方程,然后将求出的解代入所求式,很是繁冗.这里着眼整体关系,先将所求分式化简,再把x+2y-1=0变形,整体代入化简的分式求值.

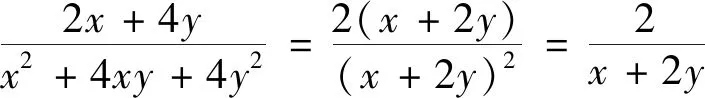
6 从差异中寻找“切入点”

数学解题的过程,从一定意义上讲,就是实现从题设到结论进行推证的过程,而识别题设与结论或量与量之间的差异,则能帮助我们寻找解题的“切入点”.

例6 (2022年江苏省南通市中考题)已知实数m,n满足m2+n2=2+mn,则(2m-3n)2+(m+2n)(m-2n)的最大值为( ).

解题是学习数学的主要手段和途径,而解题方向是否正确,解题过程是否简捷,这都需要寻找到一个好“切入点”.因此,在解题中重视寻找“切入点”,对于优化解题方案,缩短思维线路起着举足轻重的作用.