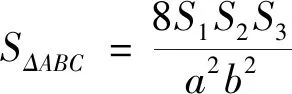三角形内切椭圆的几个几何恒等式

广东省广州市铁一中学 (511441) 范 群

文[1]给出了三角形内切椭圆的一个几何恒等式,即

命题1[1]设P,Q是ΔABC的一个内切椭圆的两个焦点,则下列等式成立:

在上述命题基础上,笔者进一步探究得到了几个新的几何恒等式.

命题2 设P,Q是ΔABC的一个内切椭圆的两个焦点,该内切椭圆与ΔABC的三边BC,CA,AB分别切于点D,E,F,则下列等式成立:

证明命题2,要用到如下几个引理.

引理1[2]椭圆切线与过切点的焦半径成等角.

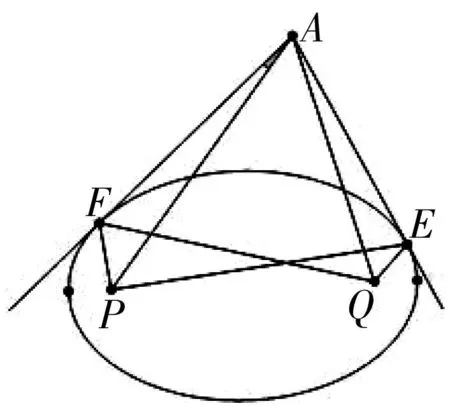
图1

引理2 如图1,P,Q是椭圆的两个焦点,AE,AF是椭圆的两条切线,则有(1)∠PAF=∠QAE;(2)∠APF=∠APE;∠AQF=∠AQE.

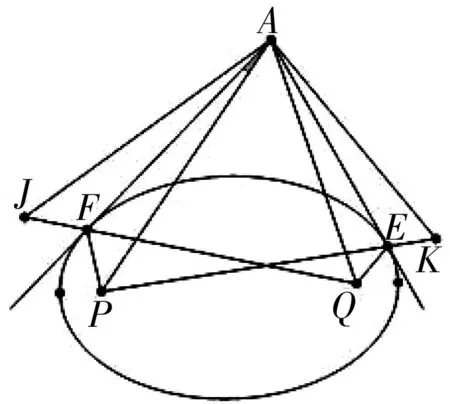
图2

证明:如图2,延长QF至点J,使得FG=FP,延长至点PEK,使得EQ=EK,由椭圆定义及引理1可推得ΔAPF≅ΔAJF,ΔAQE≅ΔAKE且PK=QJ=2a(2a为椭圆长轴长),所以有AP=AJ,AQ=AK,∠AJF=∠APF,∠AKE=∠AQE,∠JAF=∠PAF,∠KAE=∠QAE,且有ΔAJQ≅ΔAPK,所以∠AJF=∠APE=∠APF,∠AKE=∠AQF=∠AQE,∠JAQ=∠PAK,则有∠JAQ-∠PAQ=∠PAK-∠PAQ,即∠JAP=∠KAQ,也即有∠PAF=∠QAE.

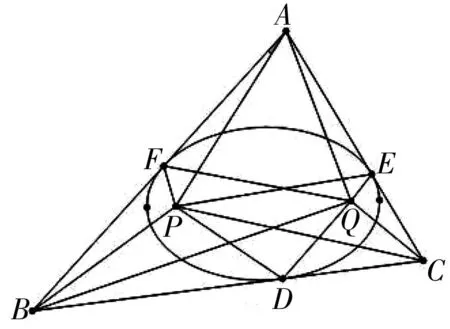
图3

引理3 如图3,设P,Q是ΔABC一个内切椭圆的两个焦点,该内切椭圆与ΔABC的三边BC,CA,AB分别切于点D,E,F(D与E,F分列在椭圆长轴的两侧),则有∠BPD=∠PAF+∠PBF+∠PCD.

证明:易知三角形内切椭圆的三个切点不能在椭圆长轴同一侧,也不能其中有两个切点都在长轴端点上或都在短轴端点上,如图3所示,三个切点分别为D,E,F,不妨设点D和E,F两点分列在椭圆长轴的两侧,则由引理1和2知,∠APF=∠APE,∠BPF=∠BPD,∠CPD=∠CPE,又因为∠APB=π-∠PAF-∠PBF,∠CPD=∠BDP-∠PCD,所以2∠APB+2∠CPD=2π,化简即可得到∠BDP=∠PAF+∠PBF+∠PCD.

若其中一个切点在椭圆长轴一个端点处,另外两个切点分列椭圆长轴两侧,也可得到类似性质,在此不在累述.

命题2的证明:如图3所示,由引理1和引理2可设∠PAF=∠QAE=θ1,∠PBF=∠QBD=θ2,∠PCD=∠QCE=θ3,∠PDB=∠QDC=α1,∠QEC=∠PEA=α2,∠QFA=∠PFB=α3,再由引理2(2)可得∠APE=∠APF=α3-θ1,∠BPF=∠BPD=π-α3-θ2,∠CPD=∠CPE=α1-θ3,∠AQE=∠AQF=α2-θ1,∠BQF=∠BQD=α1-θ2,∠CQD=∠CQE=π-α2-θ3,并由引理3可知α1=θ1+θ2+θ3.

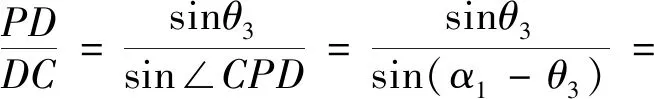
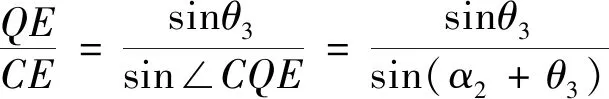
由命题1及命题2即可得

推论1 设P,Q是ΔABC的一个内切椭圆的两个焦点,该内切椭圆与ΔABC的三边BC,CA,AB分别切于点D,E,F,则下列等式恒成立:

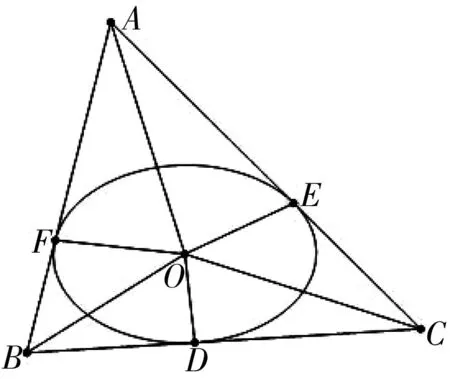
图4

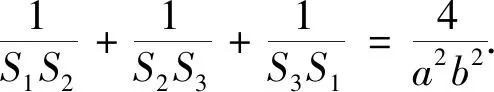
证明命题3要用到如下两个引理.

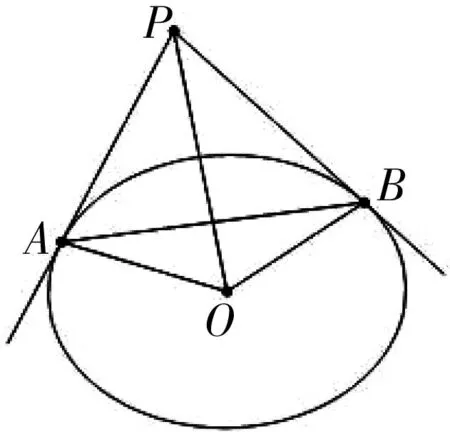
图5

引理4[3]如图5,PA,PB是椭圆的两条切线,切点为A与B,O是椭圆中心,则PO平分线段AB.

引理4的证明见文[3],此略.

引理5的证明见文[4],此略.

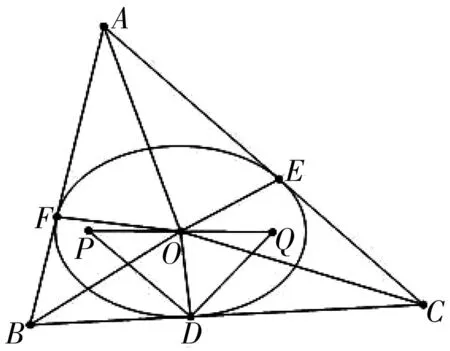
图6

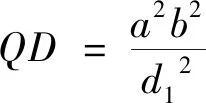
在命题3等式两边同乘2S1S2S3即可得