高中数学选择性必修课程函数主线分析*

天津师范大学教育学部 (300387) 柳 双 吴立宝

函数是现代数学最基本的概念之一,是描述客观世界中变量关系和规律的利器,更是数形结合思想的重要载体,在解决实际问题中发挥关键作用.《普通高中数学课程标准(2017年版2020年修订)》(下文简称“课标”)在明确课程基本理念中强调突出数学主线,凸显数学的内在逻辑和思想方法.[1]高中数学课程分为必修课程、选择性必修课程和选修课程,课程内容突出函数、几何与代数、概率与统计、数学建模与数学探究活动四条主线.函数主线主要分布在必修与选择性必修课程中,包括必修课程的预备知识、函数的概念与性质、幂函数、指数函数、对数函数、三角函数、函数的应用,选择性必修课程的数列、一元函数导数及其应用.但选择性必修课程函数主线内容与必修课程函数主线内容在教材编排上处于分割状,数列、导数两个单元在教学过程中易与函数主线脱节,教师不重视其中的连贯性,学生难以将数列、导数与必修课程所学函数内容联系起来.基于此,本文深入挖掘函数主线,进一步联结必修与选择性必须课程内容,明晰选择性必修课程内容与整个函数主线的联系,同时以数列单元为例进行函数主线分析,充实选择性必修课程函数部分的案例分析研究.

一、函数主线结构

站在高中数学课程整体角度上来明晰函数主线结构,认识数学知识逻辑发展,挖掘其中渗透的数学思想方法,理解数学活动的设计编排意图,发展数学学科核心素养,这是教师整体规划函数教学不可或缺的一步.参照中学数学教学内容主线分析的结构,函数主线分为知识线、活动线、思想方法线、素养线.[2]知识线是教学的根源,活动线依附于知识线,将静态的数学知识转化为动态的数学活动,思想方法线与素养线是数学教学的内隐本质,跟随知识与活动连续进阶,最终发展学生数学学科核心素养.

从知识线分析函数,按照知识发生发展的过程,剖析函数内容的知识结构、逻辑关联、本质内涵,从宏观和微观两个角度入手,让学生的认识在整体形成与局部联系中逐步结构化并螺旋上升.宏观上用十字模型,将函数产生的背景、函数概念与性质、函数模型横向连接,将函数的应用、研究函数的工具(方法)与函数性质纵向连接.函数主线的主体部分由函数概念、函数表示和函数性质组成,因生活生产需要根据函数主体构建多种函数模型,在研究函数中需要借助其他主线知识作为工具,同时将函数主线应用到其他主线之中.微观上通过梳理高中数学课程中有关函数的知识点、思想方法等,寻找知识点之间的关联,总结其知识结构,最终确定宏观结构中每个部分的微观结构.函数概念从“刻画变量之间依赖关系的数学语言和工具”(变量说)进一步抽象到“实数集合之间的对应关系”(对应关系说),在研究函数中需要借助代数运算作为基础工具、导数作为分析函数性质的工具,函数可以看作数形结合的载体之一,解析几何、平面向量几何也可以看成研究函数的工具,如图1.

图1 函数主线知识结构图

站在教师教的角度来看,活动线是知识线的活动载体;站在学生学的角度来看,知识线是活动线的内容根基.基于此,函数主线的活动线主要体现在教材编排结构和教学设计上.教材中函数内容的发展主线由“函数定义—函数性质(奇偶性、单调性、最值)—基本初等函数(指数函数、对数函数、幂函数)—函数的应用(解方程、建模)—三角函数—数列—一元函数的导数”展开,教师根据教材编排顺序,分析静态的知识线,优化教学设计,学生通过活动直接体验在“做”中感悟习得数学知识.函数主线中蕴含着重要的思想方法,函数图象与代数运算相结合的数形结合思想,证明数列简单命题的数学归纳法,在导数概念形成中体会极限思想,以及函数应用的二分法和模型思想等.数学学科核心素养的发展建立在数学知识的不断积累、数学活动的亲身经历、数学思想方法的感悟理解上,是数学教育的育人目标.在知识线和思想方法线的梳理中不难发现,函数主线的学习重点是提升数学抽象、数学建模、数学运算、直观想象和逻辑推理素养.

二、选择性必修课程函数主线分析要点

梳理选择性必修课程函数主线分析需要附着的要点,确定分析角度、找准找全联结点、厘清单元微观结构,以期突破函数主线分析现有的围栏.

1.确定分析角度

对现行人民教育出版社A版(下文简称“人教A版”)与北京师范大学出版社(下文简称“北师大版”)选择性必修教材内容进行比较分析,对比两版教材的章前引入、数列概念、导数概念、数列性质等部分,明确不同版教材对于函数模型的学习以及应用的基本过程,把握核心重点,如表1,从中发现核心概念的获得过程、知识内部的推理发展,其中蕴含的思想方法,进而凸显的育人价值极为关键.延续函数主线“知识线、活动线、思想方法线与素养线”的四条准绳,可以归纳出选择性必修课程函数主线分析要从“知识主线核心概念、知识内部推理发展、数学思想方法渗透、知识文化价值体现和应用模型”五角度展开.

表1 两版教材内容对比分析表

2.找准找全联结点

依据高中数学课程面向全体学生的理念,实现“人人都能获得良好的数学教育,不同的人在数学上得到不同的发展.”[1]高中数学课程被划分三类,函数、几何与代数、概率与统计、数学建模活动与数学探究活动四条主线贯穿于三类课程,故三类课程不是相对孤立的呈现,而是相互联系的存在.在选择性必修课程开始前,学生已通过必修课程的学习,明晰了函数的概念和性质,总结了研究函数的基本方法,掌握了一些基本函数类,探索了函数的应用.因此,找准找全选择性必修课程内容与函数主线主体的联结点是有效分析选择性必修课程函数主线的前提.在操作上分为三步,首先分析知识主线核心概念的基础性,概念的逻辑生长点,找到选择性必修课程函数知识在函数主体上的延伸处;其次分析数学思想方法的渗透,在学生已有的思想方法上继续深入拓宽边界,或者借用已有的函数思想“生长”出新的思想方法,比如学生已掌握初等函数模型,再加入特殊函数模型,实现函数模型思想方法的进阶,在“对数增长”“知识爆炸”的基础上体会极限思想.最后,分析知识育人价值的体现,能力和素养目标一般不能通过一节课的教学来实现,需要一个中长期的培养过程,[3]选择性必修课程是必修课程的补充和延伸,能力和素养势必会得到进一步的发展.

3.厘清单元微观结构

在分析知识主线核心概念、数学思想方法渗透、知识育人价值体现,找寻必修课程与选择性必修课程间联结点的过程中,已经确定单元内容的宏观结构.单元内容微观结构是指教材中本单元知识的组织安排,知识块的逻辑发展顺序,思想方法上的纵观引领,先拆分理解而后全局规划.[4]聚焦选择性必修课程中包含于函数主线的单元内容知识的微观结构,对知识的上下位关联及知识顺序进行梳理,深挖其中蕴含的数学思想方法.具体操作方法是梳理本单元教材所含的知识点堆积形成知识块,把握学生学习的重难点、关键点,列出学生学习重点知识所需的辅助性知识块,分析各知识块之间的关联,各知识块时如何发生发展的,总结其知识结构,形成知识块的网络结构图.

三、数列单元函数主线分析

数列作为一种离散函数是高中数学的重要研究对象之一,也是函数主线内容学习的一条支线,数列研究把研究对象从以往简单的“数”的研究延伸到对复杂的“一列数”的研究,包括研究它们之间的关系、规律、特征等,是对先前所学连续函数模型的延伸,也是后续深入学习离散函数的基础.

1.数列知识主线核心概念

数列单元涉及数列概念、特殊数列、数列应用和数学归纳法等.数列概念包括数列、项、首项、通项公式、递推公式、数列前n项和等核心概念,是本单元学习的起点.随后将一般数列特殊化得到等差数列和等比数列,围绕这两类特殊数列探索变化规律以及在实际问题中的应用.同时,数列概念、数列表示、数列性质、等差数列、等比数列等与函数主线主体关联,在其中感受数列与函数的共性和差异,了解数学归纳法并简单使用数学归纳法,如图2.

图2 数列单元知识结构图

数列知识主线的学习具有发展性.其一,数列与其他内容主线联系的发展性,数列属于函数主线,与不等式、方程、概率、算法、极限等其他主线知识紧密相关,是将这些内容进行综合应用的交互点.其二,在数学思想方法中的发展性,数列学习的过程中蕴藏多种数学思想方法,如函数与方程、特殊与一般、转化与化归等,这些思想方法既是函数思想的延伸,也为未来学习极限理论奠定基础.其三,现实生活应用的发展性,数列在生活中的应用十分广泛,如银行存款、汽车折旧、城市空气质量指数等实际问题,利用数列知识建立数学模型刻画其递推规律从而解决问题.

2.数列知识内部推理发展

通过日常生活和数学中的实例,掌握数列的概念和表示方法(列表、图象、通项公式),理解数列是定义在正整数集或其有限子集上的特殊函数,等差数列、等比数列属于数列的典型特例.借助情境引入等差数列,探索发现等差数列的通项公式,借高斯算法推广到等差数列的前n项和,类比等差数列通过数学史问题和生活实例得到等比数列.

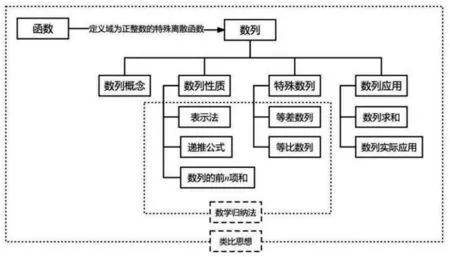
图3 数列知识块关系图

分析数列知识块之间的关系.就概念学习,在学习了集合、函数的概念、函数的表示方法和性质的基础上学习数列的概念,明确数列与函数的内在联系.就简单性质,了解数列的几种简单表示方法,对比函数获得数列的简单性质,掌握求数列通项与数列求和的方式,意在让学生了解研究数列的常见思路.就具体特例,等差数列与等比数列是两类特殊的数列,具体到探讨其通项、性质、前n项和等,通过对这两类数列的学习,实现对数列的深入探讨,强调数列和函数的内在联系,着重类比思想与数学归纳思想的渗透.就应用部分,数列是重要模型,其思想渗透在教育储蓄模型、分期付款模型等现实应用中,如图3.

3.数列实际问题应用模型

数列在现实问题中被广泛应用,同时也是古老的数学课题,在《周髀算经》里谈到等差数列的概念,《易传系辞》里有世界数学史上等比数列最早的文字记载.基于HPM视角,引导学生提出数学问题,利用数学史中的等差数列求和问题,思考等差数列求和的通项公式,进行数学化并建立数学模型解决问题.利用数学归纳法,学生将有限数项通过运算进行数学表达,最终归纳为数学公式,再与实际生活相联系.将数学与实际生活以及数学思想文化结合起来,让学生感受到数学概念的形成过程是历史上真实发生的,使数列的学习拥有现实意义.

4.数列数学思想方法渗透

数列中蕴含着丰富的数学思想方法.其一函数思想,认识到数列是一种特殊的函数.其二方程思想,通常引导学生将等差数列或等比数列的5个参量看成是变量,面对“知三求二”的题目建立方程组,求出基本量.其三演绎思想,借助情境引出数列的相关概念,从一般数列概念和性质中探索出特殊的两类数列的特征和应用意义.其四归纳思想,从高斯算法推广到一般的等差数列前n项和公式.其五类比思想,在学习等差数列的基础上类比得到等比数列的概念、性质和应用.其六数学归纳法,分析多米诺骨牌全部倒下的条件,通过猜想抽象出数学归纳法的步骤.其七分类讨论思想,利用等差数列的性质,分奇、偶两种情况解决求数列前n项和问题.其八数列求和用到的方法,累加(乘)法、错位相减法、倒序相加法、裂项相消法等.

5.数列知识育人价值体现

从函数视角看数列,数列与函数、等差数列与一次函数、等比数列与指数函数间存在关联,其中的核心概念和数学思想方法有内在统一性,学生能逐步体会到研究数学对象的基本框架和路径,学习数学的思维方式,培养理性精神.在等差、等比数列的学习中,让学生经历探索数列中项的取值规律、发现数列的性质、应用数列的性质解决问题的过程,利于学生积累数学活动经验,提高发现问题和提出问题、分析问题和解决问题的能力.数学归纳法是一种有力的证明数学命题的工具,通过其本身及蕴含的数学思想,有助于培养学生逻辑推理的素养.