教材寻法 巧解真题*
——以2023年高考圆锥曲线题为例
2024-04-15浙江省杭州学军中学海创园学校311121陶勇胜
浙江省杭州学军中学海创园学校 (311121) 陶勇胜
圆锥曲线问题是考查学生的数学运算和逻辑推理核心素养的重要抓手之一,在近几年高考及各地模拟考试中,此类问题因在求解过程中含多个变量,往往具有较大且复杂的运算量,让学生束手无策、望而生畏,是学生解题过程中的一个“痛”点.对于高考中的这一热点和难点,如果能根据已知条件,选择合适的直线参数方程,将会使得解题过程更为简洁、高效.本文先介绍直线参数方程的相关概念,再以2023年圆锥曲线高考题为例,运用直线参数方程对其进行探究,回归教材寻求突破之法.
1.直线参数方程的相关概念

图1
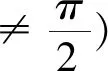
一般地,若过定点P0(x0,y0)直线l与二次曲线相交于P1、P2两点,P1,P2对应参数分别为t1,t2,则根据参数方程中的t几何意义,有以下性质:
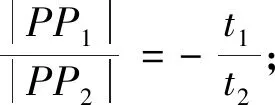
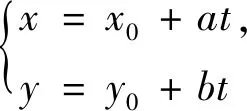
2.直线参数方程在圆锥曲线中的应用
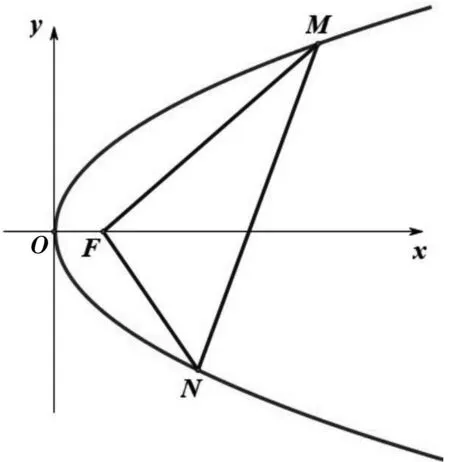
图2

解:(1)易得p=2.
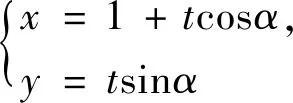
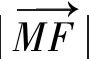
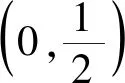
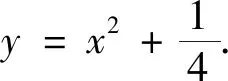

图3
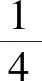
点评:该题设计巧妙、新颖,以一个边长变化的矩形“搭”在抛物线上为载体,考查矩形在滑动过程中求矩形周长的最值问题,需要学生有一定的动态思维能力,又需要在变化过程中找到不变量的逻辑推理能力.本题选择合适的直线参数方程,利用上述中的性质(1),简洁地得到矩形两边的边长,进而得到矩形周长L的表达式,突破本题的难点.由于(*)式中各项均为正,周长L的最小值只有当分子为零时取得,整个解题过程简洁、高效,避免了繁杂的运算.


图4

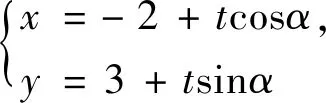
点评:该题以“若kAM+kAN为定值,则直线MN过定点”的定点问题为背景,其背景熟悉、表达简练、切入口宽.本题的关键点是由直线AP、AQ的方程得到点M、N的坐标.设直线PQ的参数方程后,便捷得到点P、Q的坐标,再结合点A的坐标,得到直线AP、AQ的方程,突破本题的关键点.显然,除了解决圆锥曲线中与长度有关的问题,直线的参数方程对于解决定点问题仍是一种十分高效的方法.实际上,此题与2022年全国数学理科乙卷第20题背景相似,也可以用直线的参数方程求解,读者可以进行尝试.
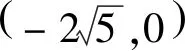

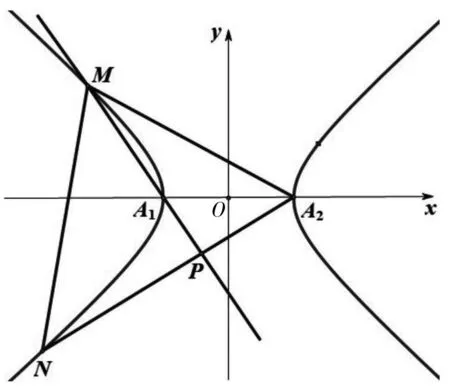
图5
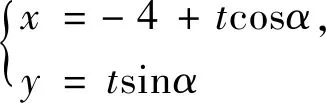
点评:该题考查直线与双曲线的位置关系,可以从多个角度理解直线MN,点M、N可以看成直线MA1、NA2与双曲线的交点,也可以看成直线MN与双曲线的交点,即选择直线MN的初始参变量不同,将导致解题过程的运算量大小不同.本题把点M、N看成直线MN与双曲线的交点,巧设直线MN的参数方程,整个解题过程中始终将t作为初始参变量,大大减少了运算量.与例3相比,例4出现了非对称韦达结构,常将sinα或cosα用t1、t2表示,转化为关于t1、t2的一次式进行化简运算,体现了转化和化归的数学思想.
3.教学启示
3.1 深究教材,为教学活动多元化奠定基础
直线的参数方程这一部分内容在新人教A版教材中以“探索与发现”的形式出现,似乎在高考中直接考查并不多,故在平时教学中容易忽视,但高三复习时,教师应充分挖掘新教材的思想,渗透新教材的方法,利用直线的参数方程开展多元化的教学活动,引导学生多题一解,拓宽学生的解题思路,在提高解题正确率的同时有助于学生摆脱解题惯性,培养学生的创新思维.
3.2 寻法教材,为破解高考真题提供良策
从近几年圆锥曲线的高考试题来看,基于教材中的数学思想和方法为出发点的命制试题不在少数,教材是教师和学生学习知识的共同载体,也是高考命题的重要依据,命题专家根据教材挖掘有价值的材料,进行命题设计,能起到良好的导向作用,教师可与学生一起在教材中“寻法”,通过教材寻求破解方法,帮助学生实现“迁移数学知识、类比解题方法,从具体的教学情境中抽象出共性、方法和体系”[1],突破机械式“刷题”,使得“减负增效”落到实处.
3.3 回归教材,为落实依标施教精准定位
章建跃博士认为:“回归教材、依标施教是高考命题改革的大势所趋,教材是从课标到教学的桥梁纽带,教学中注重用好教材,切实做到依标施教”[2].如果教师脱离教材教学,一味追求教辅上的“二级结论”,热衷“秒杀大招”,将导致学生在知识和方法迁移上捉襟见肘,遇到新的面孔,不能套路化,不会思考,长期以往,师生苦教苦学,教学效果甚微.唯有在课堂中注重教材中的通性通法,帮助学生在教师指导下,超越具体特技、特法深入到思维层面,注重学习的迁移运用和问题解决,在相似的情境中能够做到“举一反三”,才能使得学生真正成为学习的主人.
3.4 立足教材,为试题命制和解题教学把握方向
试题命制和解题教学都是教师在教学活动中不可缺少的重要技能,从教材中的数学思想和方法研究出发的试题命制和解题教学,既能帮助教师把握命题逻辑的正确性,确保命题试题的广度和深度,也能帮助教师从不同角度对高考试题引申、类比和拓展,把高考试题价值最大化,还能帮助教师能从数学的本质出发,呈现知识的生成过程,使得复习备考真正做到“精准高效”.
