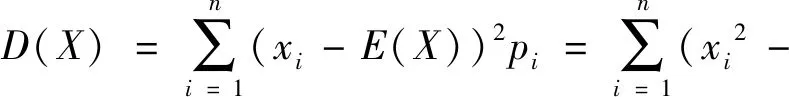构造两类概率模型解决相关不等式问题
2024-04-15广东省惠州市第一中学516007方志平
广东省惠州市第一中学 (516007) 方志平
虽然数学的各分支都有自己的研究方向和重心,但相互之间并不存在不可逾越的鸿沟.构造概率统计模型解决问题,是一种富有创造性的思维方式,它为我们解题提供了另一途径,不失为一种好方法,该方法对于培养学生思维的广阔性和创造性,具有重要的意义.本文尝试构造两类概率模型解决相关不等式问题,旨在为探索解题新路抛砖引玉.
1.构造独立事件,巧用概率性质证明
利用概率思想,通过构造恰当的概率模型,解决一些其他数学分科的问题,是一种别开生面的解题方法.概率的性质很多,其中概率的加法公式:设A,B,C是一个随机试验中的三个事件,则P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(CA)+P(ABC).它对于解决一些不等式问题,常常表现出简捷、明快、精巧、新颖的特点,使数学解题突破常规,具有很强的独特性和创造性,也彰显了数学的永恒魅力!下面举例说明.

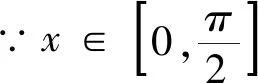
评注:本题是通过局部分析法,将“二倍角”与“和角”都化为单角,得到sinx+cosx-sinxcosx≤1.由于0≤sinx≤1,0≤cosx≤1.让我们不难联想到构造概率,利用两独立事件的加法公式帮助证明.
例2 已知0 证明:设A,B,C是三个相互独立的事件,且P(A)=a,P(B)=b,P(C)=c.由概率加法定理和事件的独立性得P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(CA)+P(ABC).∴P(A+B+C)=a+b+c-ab-bc-ca+abc,由已知条件0 评注:由条件与所证不等式的结构特征,让我们联想、类比三个独立事件的加法公式.可见观察与联想是寻找解题的突破口. 例3 若0 评注:由于0 评注:由于a,b,c是三角形三边长,且a+b+c=1, 于是要先寻找构成三角形时a,b,c所满足的条件.另外,条件a+b+c=1在证题时多次被利用,也是证明本题的一个关键点. 利用这一结论,在解决有关不等式问题时,若能根据不等式的结构特征,巧妙地构造离散型随机变量的概率分布列去解决问题,则可另辟蹊径,往往会给人耳目一新的感觉. 例5 已知实数x,y,z满足方程x+2y+3z=12,求x2+2y2+3z2的最小值. 评注:观察条件与所求式子的结构形式,逆向思考,联想构造离散型随机变量的分布列,再求随机变量的期望,巧用方差公式D(X)=E(X2)-(E(X))2≥0,问题则顺利得到解决. 例6 (2012年全国高中数学联赛江西预赛题)若实数a,b,c满足a+b+c=a2+b2+c2, 则a+b+c的最大值是. 评注:构造概率模型是通过对条件和结论充分细致的分析,抓住问题的特征,设出a+b+c=a2+b2+c2=t,以此架起一座连接条件和结论的桥梁,挖掘问题与概率思维的共性. 例7 (2013年全国高中数学联赛B卷)假设a,b,c>0, 且abc=1, 证明:a+b+c≤a2+b2+c2. 评注:由于正数a,b,c满足a+b+c=1,隐藏着0 以上各例,虽然我们用常规的方法也可以去解决,但利用构造概率的方法解题,不仅为我们提供了解决关于一些不等式问题的新方法,而且拓宽了我们的解题思路, 使复杂问题简单化,从而提高了解题的效率.
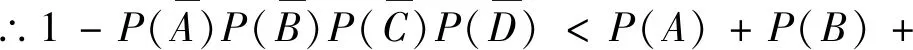
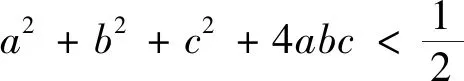

2.构造分布列,巧用方差公式解题