由一道高考模拟题探究圆锥曲线恒过定点问题*

聊城大学数学科学学院 (252000) 张瑞雪 房元霞 徐茂林

由于圆锥曲线作为坐标平面内点的运动轨迹,蕴含着运动变化过程中保持的某种“规律性”或“不变性”[1],而这种“规律性”或“不变性”就是圆锥曲线的性质.本文以2023年某市高三二模第21题为例,利用GeoGebra软件探究圆锥曲线的定点问题.

一、题目

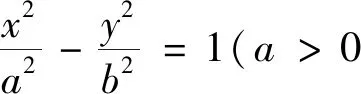
(1)求该双曲线C的方程;(2)若直线l与双曲线C在第一象限交于A,B两点,直线x=3交线段AB于点Q,且SΔFAQ:SΔFBQ=|FA|:|FB|,证明:直线l过定点.

本题以双曲线为载体,考察转化和联立方程的计算能力,第(2)问更是蕴含了圆锥曲线一般性结论.我们设直线l与双曲线C交于任意两点A,B,直线x=3推广至垂直于坐标轴的直线x=t(或y=t),然后利用GeoGebra软件探究得到如下情形与结论.

二、推广到一般

图1

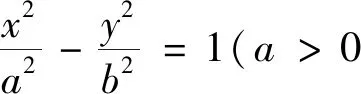
注:本文仅以焦点在x轴上的圆锥曲线为例进行证明,焦点在y轴上的证明不再累述.

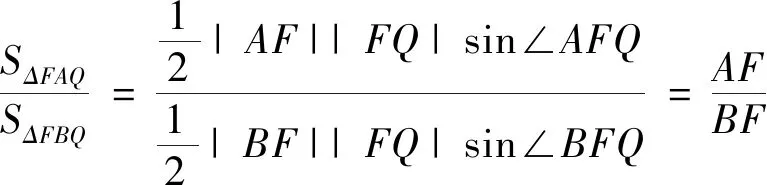
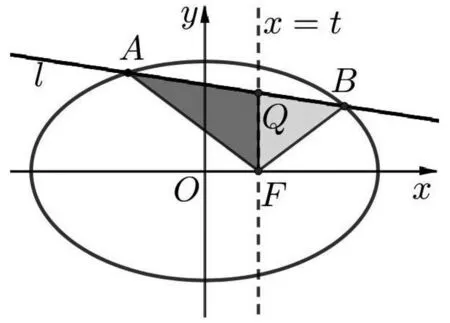
图2

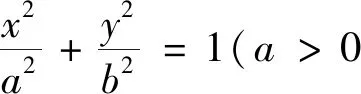
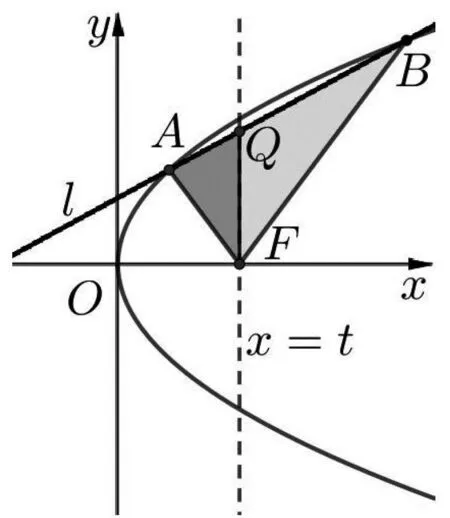
图3

定理3 设抛物线C:y2=2px,若直线l与抛物线C交于A,B两点(如图 3),直线x=t交线段AB于点Q,交x轴于点F,且SΔFAQ:SΔFBQ=|FA|:|FB|,则直线l过定点(-t,0).

图4

定理4 设抛物线C:x2=2py,若直线l与抛物线C交于A,B两点(如图 4),直线y=t交线段AB于点Q,交x轴于点F,且SΔFAQ:SΔFBQ=|FA|:|FB|,则直线l过定点(0,-t).

注:针对抛物线y2=2px直线y=t的情形,由于证明过程中m与k存在反比例关系,即无法证明定点与变量k无关,所以此种情况抛物线不过定点,类似的,抛物线x2=2py直线x=t的情况同样不过定点.

上述,我们从双曲线出发,通过类比、猜想、实验、证明等数学思想方法的指引,得出了椭圆、双曲线、抛物线三种圆锥曲线一般性的结论,“对圆锥曲线进行一般化推广,变的是曲线,不变的是方法,将问题进行一般化的推广,有助于学生进一步认识圆锥曲线的性质.”[2]启发学生做一道题,要学会解一类题,拓展自己的解题空间,培养数学思维的广阔性、灵活性和深刻性,进而发展创造性.