激光振镜直写光栅误差分析及校正方法
2024-01-15任东旭周梦园
任东旭,周梦园,牛 奚,李 彬
(中原工学院机电学院,机械工业光学传感与测试技术重点实验室,河南 郑州 451191)
1 引 言
激光直写(SBIL)光栅技术是利用能量密度高、高集束性的激光对基底面的光刻胶进行曝光刻蚀,经过后期显影后形成明暗相间的光栅条纹。相对其他光栅制造技术,激光直写具有成本低、效率高和加工尺寸大等优点[1]。激光振镜是利用两个相互垂直的振镜电机的快速偏转带动反射镜从而改变激光光路,振镜惯量小,重复定位精度高[2]。能够使激光直写光栅的加工效率得到明显的提升。但振镜系统存在着几何畸变[3]、离焦[4]、非线性[5]等多种因素引起的误差。
在现有振镜误差补偿方法中。朱铁爽[2]等人提出了一种视觉辅助的畸变校正方法,以机器视觉代替人工获取振镜系统误差并对误差进行拟合补偿。这种方法效率低下,无法快速连贯的刻划光栅条纹。赵中民[6]等人将振镜误差分为了测距误差、角度误差以及枕形误差,并分别对其进行了优化补偿,但方法效率低,不适合工业使用。彭留永[7]等人对振镜误差的角度误差进行了分析,使用多项式的方式对优化。但优化效果在大尺寸范围内,误差降低效果并不明显。贾和平[8]等人建立了基于平面坐标变换几何矫正算法的模型,从而降低了系统误差,但这种方法系统计算量太大,降低了扫描效率。韩万鹏[9]等人的方法不适用于激光直写光栅。
针对激光直写光栅的特点,本文对振镜镜片的转角计算公式作了优化,针对光栅条纹的特性,进一步对扫描误差进行了曲拟合补偿。降低了直写光栅条纹的误差量,提高了激光直写系统单次扫描的范围。
2 振镜扫描误差分析与补偿
2.1 振镜扫描误差分析
激光振镜系统可分为前扫描方式和后扫描方式,本文采用前扫描方式,如图1所示。

图1 激光振镜前扫描方式
入射激光在经过振镜的两个反射镜后到达F-theata场镜,后经过场镜的聚焦在工作面上进行光栅条纹的扫描刻蚀。前扫描方式存在着枕形和桶形的复合畸变[10]。
在理想状态下,振镜扫描的坐标与振镜电机转角的映射关系为:
(1)[11]
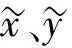
为了减小逻辑运算量并提高实时性,一般采用简化的控制策略代替复杂的坐标-转角映射关系[2]。振镜的x,y电机转角∂x、∂y并非是按式(1)进行计算。工业使用中常用如下式进行计算镜片电机转角。
(2)[12]
式中,f为振镜焦距。
以单侧光栅长度10 mm为例,将∂x、∂y代入下式进行误差计算:
(3)
本文采用FOTIA工业纳秒激光器,激光光束直径0.45 mm,波长355 nm。卡门哈斯振镜,焦距f=420 mm。结合公式(2)与公式(3),通过matlab进行误差模拟仿真结果如图2所示。

图2 激光振镜扫描误差三维分布图
如图2所示,振镜系统产生的误差随着x、y的不断增大而增大。本文中预期光刻扫描光栅栅距为10 μm,表一所列,在(100,10)点x向误差已经达到了9 μm。无法直接应用于激光直写光栅中。
2.2 激光振镜转角优化补偿
经过上述分析,可见振镜系统产生的系统误差主要由振镜的转角简化引起的,所以需对振镜转动角度进行优化,从公式(1)可以推导出正确的转动角度为:
(4)

联合公式(2)、公式(4)推导出振镜的转角误差计算式为:
(5)
从公式(5)中,当Δ∂x中的y为0时差值为0,所以角度误差来源于y值的省略,因此本文引入f(y)对∂x进行优化校正,同理对∂y引入f(x)进行优化,其振镜扫描误差较正后如下:
(6)
根据公式(6),采集一系列特征点,计算相应的振镜转角优化系数。如表2所示。
通过matlab对表中数据f(x)、f(y)进行数据曲线拟合,得到振镜转角优化系数计算式:
(7)
优化后振镜转角为:
(8)
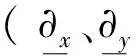
将优化后的角度公式式(8)代入式(3)联合,通过matlab仿真作图,如图3所示。

图3 角度优化后振镜系统误差
将图3与图2对比可以很明显的看出,其误差得到了明显的缩减。但误差的增长速率并未得到很好的改善,累计误差增长速率过快仍然对激光直写光栅条纹有着很大的影响。
2.3 振镜坐标误差补偿
为了改善振镜扫描误差的增长趋势过快的缺陷,降低光栅条纹的累计误差程度。本文在振镜转角优化的基础上又对其扫描坐标误差进行了拟合补偿。
根据光栅条纹的特点,在y向长度取20 mm,由于y向的取值最大为20 mm,其引起的误差对于光栅条纹的精度影响可以忽略,同时为了较小系统计算量,增加激光直写的效率,所以采集数据时不对y值进行变化取值。
将x轴每间隔10 mm上下两端各10 mm处作为误差采集点。
对曲线拟合经验公式进行适配修改:
(9)
根据式(8),计算出图4中的采集点相应的误差,如表3所示。

图4 振镜扫描误差采集点
根据表3中的数据,结合式(9),得到相应的k值,并通过数据拟合得到k值的拟合公式:
(10)
将上述所有研究联合起来得到最终误差补偿的振镜坐标与转角映射公式:
(11)
2.4 误差优化补偿结果
取一组理想的扫描点,用式8计算出优化过的角度,并将其代入式(11)计算出优化补偿后的坐标,如表4所示。
对比表1与表4,可以明显看到误差得到了非常明显的降低。对于目标栅距10 μm的光栅条纹刻线,单次扫描中的最大栅距误差降低了98.5 %。

表1 振镜刻线误差

表2 振镜转角优化系数
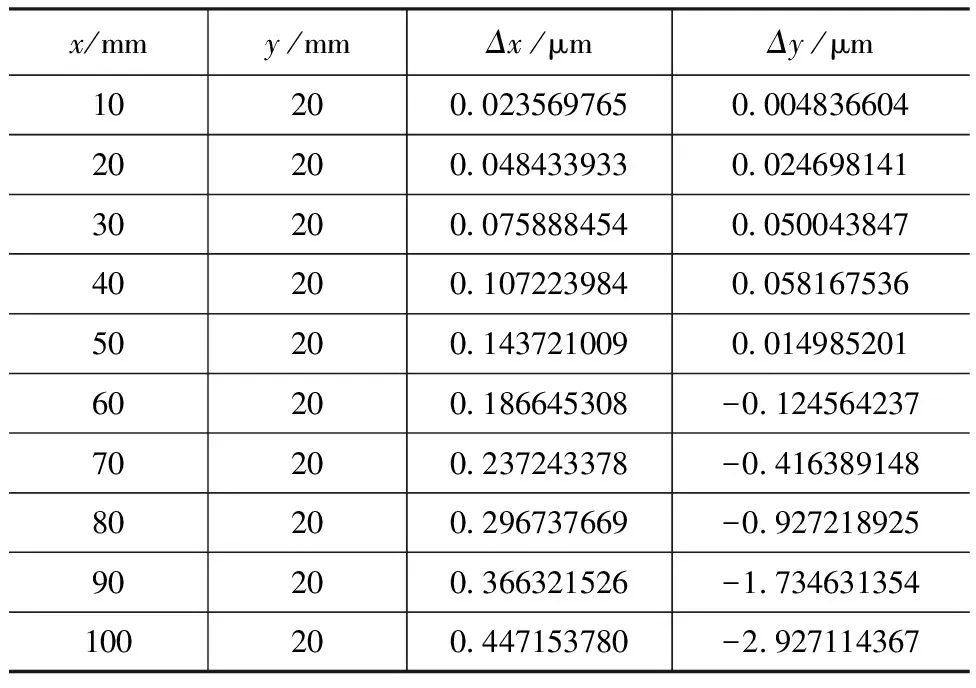
表3 采集点误差表
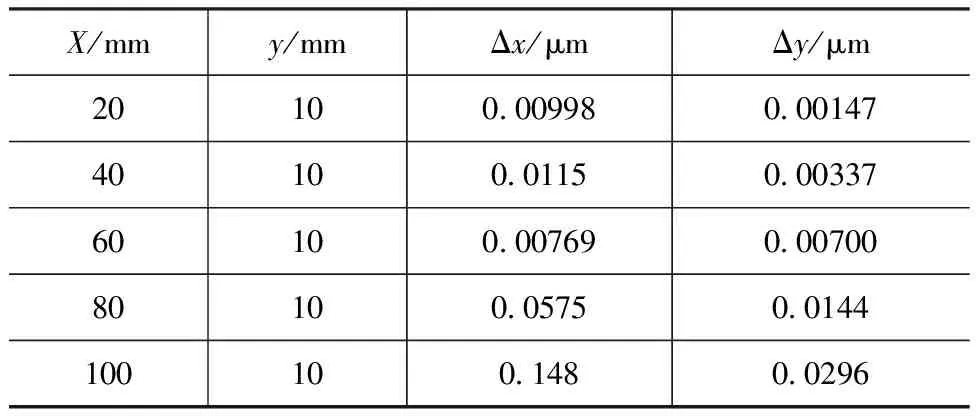
表4 优化补偿后振镜误差
通过matlab对式11进行仿真作图,如图5所示。相较于图1,振镜的误差增加速率得到了较大的降低。
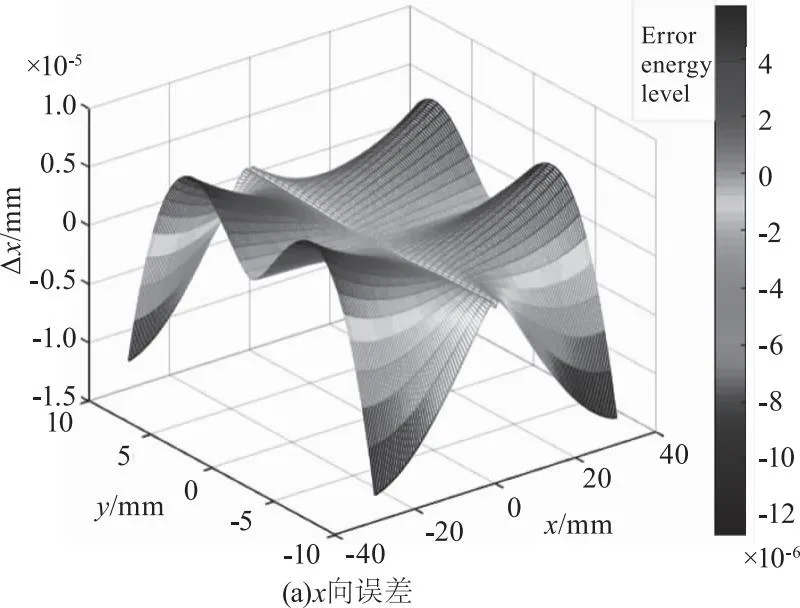
图5 优化补偿后振镜扫描误差
3 结 论
本文对基于振镜系统的激光直写光栅系统中的振镜系统误差进行了误差分析,并建立了振镜扫描坐标的数学模型,对转角计算式优化的公式做出变革优化,并针对激光直写光栅的特点,对振镜坐标误差进行了误差补偿,将200 mm范围内最大栅距误差降低了98.5 %。降低了栅距误差的增长速率。对于基于振镜的激光直写光栅系统提供了一定的理论支持。
由于振镜转动电机的限制,振镜的扫描范围并无法实现大尺寸的光栅刻划,在后续的研究中,可以增加精密运动台,实现运动台与振镜的结合,从而实现大尺寸的扫描刻线。本文得研究方法能够对于不同的刻划需求进行快速便捷的数据变更,其在集成电路、生物医疗、激光雷达和激光加工等诸多领域的应用前景非常广阔。
